直流电压下SF6气体中电极覆膜对金属微粒启举的影响机理

律方成 刘宏宇 李志兵 董 蒙 颜湘莲

（1. 新能源与电力系统国家重点实验室（华北电力大学） 北京 102206 2. 中国电力科学研究院 北京 100085）

直流电压下SF6气体中电极覆膜对金属微粒启举的影响机理

律方成1刘宏宇1李志兵2董 蒙1颜湘莲2

（1. 新能源与电力系统国家重点实验室（华北电力大学） 北京 102206 2. 中国电力科学研究院 北京 100085）

为研究直流电场下SF6气体中低压电极覆膜对金属微粒启举的影响机理，搭建了实验平台并使用高速摄像机记录运动轨迹。实验结果表明，随着SF6气体压力的增大，微粒启举场强升高，且启举后到达高压电极的时间缩短。基于图像处理获得了微粒的瞬时位移，结合运动力学方程和最小二乘法提出了启举时电荷量的计算方法，微粒电荷量的计算分析表明启举时的电荷量减小。建立了覆膜后金属微粒周围电场分布的理论模型，电场分析表明金属微粒与薄膜间的电场明显增大及表面电荷密度分布的改变，使得金属微粒受到向下的极化作用力。研究认为：电荷量减小和极化作用力向下综合导致金属微粒的启举场强提高；覆膜后局部放电是金属微粒的带电机理；SF6气体压力增大使得金属微粒发生局部放电的起始场强升高，导致极化作用力增大，需要更高场强发生启举。

直流电压 SF6气体 电极表面覆膜 电荷量 极化作用力 金属微粒启举

0 引言

气体绝缘金属封闭输电线路（Gas Insulation Line, GIL）因其输送能力强、占地面积小、可靠性高等优点成为未来远距离、大规模输电的一种重要选择方式[1]。然而，GIL在加工、运输、安装、运行过程中将不可避免地产生金属微粒[2]，由金属微粒运动导致的绝缘性能下降是GIL在工程应用中亟待解决的问题之一[2,3]。

低压电极表面覆膜是抑制金属微粒运动、改善金属微粒污染的一种重要措施，通过实验测量覆膜后金属微粒的启举场强，并和裸电极结果进行比较是研究覆膜对金属微粒启举场强影响的常见思路[4-6]。基于该思路，文献[4,5]研究了交流电压下SF6气体中金属微粒（不锈钢球）在电极表面分别覆氧化铝膜、聚乙烯膜时的启举场强，文献[6]研究了交流电压下N2/SF6气体中线形金属微粒（铝质）在电极表面覆改性邻苯二甲酸酯膜时的启举场强，结果均表明在0.1～0.4MPa范围内，随着气体压力增大，金属微粒的启举场强提高。

上述电极表面覆膜对金属微粒启举影响的研究均在交流电压下进行。与交流电压相比，直流电压下金属微粒受到单一方向的电场作用力在电极间发生贯穿性运动，导致金属微粒污染问题更加严重，因此直流电压下覆膜的研究显得尤为重要。但目前对此研究较少，大部分工作在空气中开展[7,8]。此外，电极表面覆膜后，阻止了金属微粒与电极接触时的直接带电，金属微粒与薄膜间的传导或局部放电成为金属微粒带电的主要机理，和裸电极相比金属微粒所带电荷量可能发生变化[8,9]，因此，明确金属微粒启举时的电荷量对研究电极表面覆膜对金属微粒启举的影响机理具有重要意义。

综合考虑直流电压下SF6气体中有关覆膜研究较少及金属微粒启举时的电荷量这一参数的重要意义，本文搭建了直流电压下SF6气体中电极表面覆膜后金属微粒启举的实验平台，获得了金属微粒的启举场强及运动图像；金属微粒运动图像处理方法（中值滤波、背景差分、形态学滤波）、运动力学方程、最小二乘法相结合计算得到了金属微粒启举时的电荷量；探讨了覆膜对金属微粒启举的影响机理;最后从机理上定性分析了SF6气体压力对金属微粒启举场强的影响。

1 金属微粒启举实验

1.1 实验平台

图1 金属微粒启举实验平台Fig.1 Experimental platform of metallic particle lift-off

金属微粒启举实验平台如图1所示。将平行板电极放置在可充SF6气体的密闭罐体中，直流电压通过套管施加到平行板电极上极板，下极板接地，罐体表面设置观察窗，使用高速摄像机观测并记录金属微粒启举后的运动轨迹。为保证图片拍摄清晰，利用LED可调光源进行补光。其中，平行板电极的材质为黄铜，极板直径为20cm，厚度为5mm，极板边缘通过圆角处理，圆角半径为0.5mm，电极间距为10mm；低压电极所覆薄膜的材质和文献[7-9]相同，为PET（相对介电常数3.8，电导率1×10-14S/m），厚度为100μm；金属微粒为直径1mm的铝球（密度为2 800kg/m3）。

实验基本步骤：

1）用浸有无水乙醇的丝绸擦拭电极和金属微粒保证金属微粒与电极表面洁净，待乙醇完全蒸发后，将金属微粒放置在下极板中心位置。

2）使用SF6气体回收回充设备（RF-051）对封闭罐体进行抽真空（真空度至120Pa）、充一定压力（0.1MPa、0.15MPa、0.2MPa）的SF6气体。

3）为方便后续图片处理，设置高速摄像机的帧率为1 000fps。调节高速摄像机控制软件中的色温参数，使平行板电极间隙整体背景呈绿色、金属微粒呈黑色。

4）通过直流高压发生器（FVG-±150kV）进行加压，升压速度为0.32～0.36kV/s，直至金属微粒启举。

5）保存高速摄像机拍摄的金属微粒启举后的运动图片，回收SF6气体，记录金属微粒启举时的电压数值并根据公式E=U/d换算为场强数值，每组实验测量3次，得到金属微粒的平均启举场强E。

1.2 实验结果分析

表1为覆膜后不同气压下金属微粒的启举场强及与裸电极的对比结果。由表1可知，与裸电极相比，覆膜后金属微粒的启举场强明显提高；随着SF6气体压力的增大，金属微粒的启举场强增大。

表1 金属微粒的启举场强Tab.1 Lift-off field of metallic particle

图2为不同气压下金属微粒启举后的运动图像。由图2可知，金属微粒启举后将向平行板电极上极板运动直至发生碰撞，且随着SF6气体压力增大，到达平行板上极板所需的时间变短。

图2 金属微粒运动图像Fig.2 Motion image of metallic particle

2 金属微粒启举时电荷量的计算方法

2.1 电荷量计算原理

金属微粒启举后将在静电力、重力、气体阻力的作用下向平行板电极上极板加速运动[10]。根据文献[10]中气体阻力计算公式，对于1mm铝球，在0.10MPa、0.15MPa、0.20MPa三种气体压力条件下受到气体阻力Fd与重力G的对比结果如图3所示。由图3可知，当微粒速度为0～3m/s时，0.10MPa和0.15MPa下气体阻力小于重力，0.20MPa下微粒的气体阻力可能略大于重力，但仍在同一个数量级。而由图2简单估算可知，微粒启举后到达高压电极的时间不大于10ms，因而微粒运动的加速度应大于200m/s2，是重力加速度g的20倍以上，电场力的作用远大于气体阻力和重力，表明当微粒速度在0～3m/s之内时，受到的气体阻力可忽略。

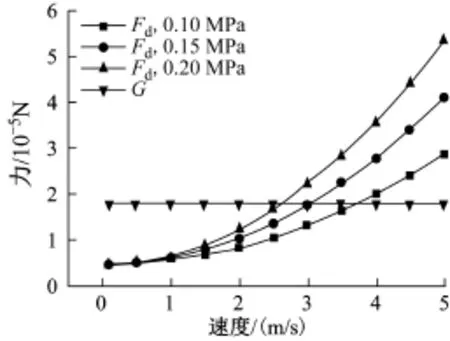
图3 阻力与重力对比Fig.3 Comparison of drag force and gravity

假设运动过程中金属微粒所带电荷量q不发生变化[10,11]，则金属微粒受到的静电力不变，意味着金属微粒将以加速度a向平行板电极上极板做匀加速直线运动，运动力学方程为[8,10]

式中，m为金属微粒质量，对于直径1mm的铝球，m=1.47×10-6kg；s为金属微粒的瞬时位移；g为重力加速度，g =9.81m/s2；E为金属微粒的启举场强；q为金属微粒所带电荷量。

由式（1）可得

分析式（2）、式（3）可知：若能够获得金属微粒在极板间运动的加速度a，则可计算出金属微粒启举时电荷量q，而加速度a与金属微粒的瞬时位移s密切相关，因此精确获得金属微粒的瞬时位移显得尤为重要。

2.2 基于图像处理的金属微粒瞬时位移计算方法

为精确获得金属微粒运动的瞬时位移，本文基于图像处理方法对金属微粒运动图片进行如下处理：1）首先采用中值滤波算法提取出实验中金属微粒运动的背景图像，其基本原理是将运动图片中一点的像素值用该点的一个邻域中各点像素值的中值代替，让周围的像素值接近真实值，即[12]

式中，B(x,y)、I(x,y)分别为原始图像和处理后图像；W为二维模板，通常为33、55区域，也可以是不同的形状，如线状、圆形、十字形、圆环形等。

2）利用背景差分法将金属微粒运动图像与背景图像相比较，可得到差分图像D(x,y)[12]。

若差分图像同一位置的像素点数值大于一定阈值，则认为是由小球运动特征所造成的变化，保留该差分图像即可得到小球运动的位置信息。

3）由于所得到的差分图像有部分噪声存在，干扰了对小球位置的判定，将差分图像进行二值化处理得到二值化图像T(x,y)[12]。

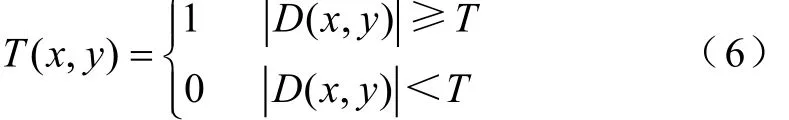
式中，T为阈值，本文中T =0.2。采用形态学滤波的开闭运算对二值化处理过的图像进行降噪，滤除不相干的噪点[13]。

式中，E为工作空间；B为结构元素；◦为形态学开运算；·为形态学闭运算；⊗为腐蚀运算；⊕为膨胀运算。

经过图像处理步骤1）～步骤3）后，即可得到只包含小球的准确图像，图4为0.20MPa时经过图像处理后的运动图像。

图4 处理后的运动图像Fig.4 Motion image after processing

获得只包含金属微粒的准确图像后，可精确获得金属微粒的像素坐标，像素坐标与金属微粒瞬时位移之间的转换公式为

式中，yu、yd分别为平行板电极上、下极板的像素坐标；yp,i为每帧图像中金属微粒的像素坐标。不同气压下金属微粒瞬时位移的计算结果见表2。

表2 金属微粒瞬时位移计算结果Tab.2 Instantaneous displacement calculation result of metallic particle

2.3 电荷量计算结果

以式（2）为目标公式，利用经典最小二乘法拟合算法对不同时刻金属微粒运动的位移进行曲线拟合[14]，结果如图5所示。表3为不同气压下金属微粒运动的加速度a及根据式（3）得到的金属微粒启举电荷量计算结果。此外，在明确加速度a后，根据匀加速直线运动的速度计算公式v=at计算可知，三种气压条件下微粒的最大速度不超过3m/s，在图3微粒速度范围内，进一步表明了气体阻力可忽略。

图5 位移曲线拟合结果Fig.5 Displacement curve fitting results

表3 金属微粒加速度及其电荷量计算结果Tab.3 Acceleration and charge quantity calculation result of metallic particle

3 电极表面覆膜抑制金属微粒启举的机理分析

3.1 覆膜对金属微粒启举电荷量的影响

为与裸电极时金属微粒的电荷量对比，根据Pérez等理论推导的裸电极下金属微粒与平行板电极下极板接触时电荷量计算公式[15]

对裸电极下金属微粒在启举场强下的电荷量进行计算，结果见表4。对比表3和表4可知，覆膜后金属微粒的电荷量减小，在0.10MPa、0.15MPa、0.20MPa三种气压条件下，金属微粒电荷量分别为裸电极时的51.78%、47.52%、50.60%。

表4 裸电极下金属微粒带电量理论值Tab.4 Theoretical value of the charge quantity of metal particle on the bare electrode

3.2 覆膜对金属微粒周围电场分布的影响

忽略金属微粒与电极之间的分子吸引力,金属微粒能够启举是因为其受到的向上的麦克斯韦应力大于向下的重力[16],而麦克斯韦应力与金属微粒周围的电场分布有关，因此有必要计算获得金属微粒存在时电极间隙的电场分布，并和裸电极进行对比。

对于裸电极下的金属微粒，其电位φ 满足[7]

式中，φHVE、φGE分别为平行板电极上、下极板的电位；φp为微粒的电位。

对于覆膜时的金属微粒，金属微粒初始电荷量为0pC，其电位φ 满足[16,17]

式中，Γ为微粒表面。

为对比裸电极和覆膜后金属微粒周围电场分布的差异性，以SF6气体压力为0.15MPa时金属微粒的启举电压为例，平行板电极间隙场强为4.80×106V/m。

英格兰校园足球协会通过四级竞赛机制组织并促进校园足球运动的发展，它们分别是：学校内部比赛、学校间比赛、郡区级校园足球比赛、国家级校园足球比赛。

图6为裸电极和覆膜下金属微粒附近的电场强度分布。由图6可知，裸电极下场强的最大值在金属微粒顶端，而覆膜后金属微粒电场强度最大值出现在金属微粒与薄膜之间，且高于裸电极时金属微粒场强的最大值。这可表明覆膜的存在使得金属微粒周围的电场分布发生了极大改变。

图6 电场强度分布云图Fig.6 Electric field distribution contour

3.3 覆膜对金属微粒表面电荷分布及麦克斯韦应

力的影响

图7 表面电荷密度分布Fig.7 Surface charge density distribution

在电场作用下，金属微粒表面的电荷分布亦发生变化，图7为裸电极和覆膜下金属微粒表面的电荷密度分布，其中横坐标为微粒表面到金属微粒底端的垂直距离。由图7可知，对于裸电极，金属微粒表面的电荷密度总为负极性，越远离金属微粒底端，电荷密度数值越大，这和图6a中电场强度在金属微粒顶端达到最大值的结果一致。电极表面覆膜后，在电场作用下金属微粒发生了极化，表面电荷密度在距离金属微粒底端0.435mm处由正极性转变为负极性，从而使得金属微粒的上、下半周产生等量的异种电荷（数值计算结果：上半周-132pC、下半周131pC）。

受表面电荷分布变化的影响，裸电极和覆膜下金属微粒表面受力明显不同。图8为裸电极和覆膜下金属微粒受到的竖直方向的麦克斯韦应力密度分布。由图8可知，对于裸电极，金属微粒在微粒表面各位置受到的应力密度均为正值，使得金属微粒整体受到向上的电场作用力（称之为静电力）。覆膜后，微粒的麦克斯韦应力密度发生变化，微粒下半周的麦克斯韦应力密度为负值，上半周的麦克斯韦应力密度为正值，这是由金属微粒表面的电荷密度分布决定的。正、负电荷在低压电极内部产生镜像电荷，在两种电荷及其镜像电荷的作用下，金属微粒受到向下的吸引力（称之为极化作用力）[18]。

图8 竖直方向麦克斯韦应力密度分布Fig.8 Maxwell stress density distribution in the vertical direction

上述对电荷密度分布及麦克斯韦应力密度的分析可表明：覆膜后即使金属微粒不带电，其仍然受到向下的极化作用力。S. P. Hornfeldt和J. Q. Feng进一步指出：对于带有一定电荷量的金属微粒，其与薄膜表面接触时该极化作用力仍然存在，此时金属微粒受到的电场作用力可认为是静电力和极化作用力的叠加，也即微粒带电后仍需考虑金属微粒受到的极化作用力,而当金属微粒离开薄膜后，极化作用力立刻消失[18,19]。

由上述分析可知，与裸电极相比，覆膜使得金属微粒启举时所带的电荷量小于同等条件下裸电极的电荷量。此外，金属微粒与薄膜间的场强大大增加，金属微粒的电荷密度分布发生了变化，使得金属微粒受到向下的极化作用力。电荷量减小和极化作用力向下是覆膜抑制金属微粒启举的两个因素。

4 金属微粒的带电机理分析

已有研究结果表明：覆膜阻止了金属微粒与电极接触时的直接带电，传导或局部放电成为金属微粒带电的主要机理。若传导为覆膜后金属微粒的带电机理，则金属微粒的启举场强与SF6气体压力无关；反之，若局部放电为覆膜后金属微粒的带电机理，则金属微粒的启举场强与SF6气体压力有关[17,20,21]。根据本文1.2节实验结果：金属微粒启举场强与SF6气体压力相关，可初步推断局部放电为直流电压下SF6气体中电极表面覆膜后金属微粒的带电机理。

此外，由上文对金属微粒电场分布的分析可知，覆膜使得金属微粒与薄膜之间的场强大大增加，根据高电压相关理论可知，较大的场强可能会引起金属微粒与薄膜之间发生局部放电，使得金属微粒带电。为此，本文基于气体放电的流注起始判据对金属微粒的带电机理展开进一步分析[17,21-24]。

式中，α、η 分别为气体的汤逊第一电离系数和附着系数，m-1；l为电子崩长度，在最外层边界满足α =η；K为气体放电常数，K=10.5[23-25]。不同研究人员给出的SF6气体有效电离系数αη-的表达式略有不同，本文计算时取

式中，p为SF6气体压力（MPa）；E为沿着电子崩发展最优路径的电场强度（V/m）。对于电子崩发展最优路径的选择，应满足式（12）的计算结果最大[17,26]，虽然金属微粒与膜接触的部位电场最大，但其路径距离为0。因此，电子崩发展最优路径的起始点并不在金属微粒与薄膜的接触点，而是在其附近，其典型的积分路径示意图如图9所示。

图9 电子崩发展路径示意图Fig.9 Schematic of electronic avalanche development path

表5为不同气压下金属微粒与薄膜之间发生局部放电的起始场强。由表5可知，该数值小于实验获得的金属微粒的启举场强（图2）。此外，本文计算气体放电的流注起始判据模型中尚未考虑电子崩中正、负离子的作用，若考虑正、负离子，则金属微粒的局部放电起始电压可能会变得更低[27]，这更进一步证实了局部放电为覆膜后金属微粒的带电机理。

表5 局部放电起始场强计算结果Tab.5 Calculation results of partial discharge initial electric field

5 SF6气体压力对金属微粒启举的影响分析

基于上述直流电压下SF6气体中电极表面覆膜对金属微粒启举的影响机理分析，本文对“金属微粒启举场强随着SF6气体压力增大而增大”这一实验结果进行如下解释：

1）对于放置在覆膜电极表面的金属微粒，在局部放电机理下金属微粒带电，局部放电的起始场强与SF6气体的有效电离系数密切相关。由式（13）可知，SF6气体的有效电离系数随着气体压力的增大而减小，这是因为气体压力越大，分子之间的间隙减小，电子的自由程变短，在相继两次碰撞间从电场获得的能量小，电子就不容易引起气体分子电离，同等条件下需要更高的电场才能满足发生局部放电的起始条件（如图10所示），也即覆膜后金属微粒因局部放电而带电所需的场强增大。

图10 局部放电起始场强与气压关系Fig.10 Relationship between initial electric field of partial discharge and gas pressure

2）金属微粒与薄膜接触时，一直受到向下的极化作用力，其与平行板电极间的场强有关。图11为不同场强下金属微粒受到的极化作用力的计算结果及金属微粒启举所需的电荷量。由图11可知场强越大，极化作用力越大；极化作用力的增大又使得金属微粒需要带更多的电荷量克服金属微粒向下的极化作用力和重力，进一步导致了金属微粒的启举场强升高。

图11 极化作用力、启举临界电荷量与场强关系Fig.11 Relationship between the polarization force、the critical charge and the electric field

6 结论

1）提出了覆膜后金属微粒启举时电荷量的计算方法，获得了启举时的电荷量，同等条件下和裸电极相比，该数值减小。

2）覆膜使得金属微粒与薄膜之间的电场强度明显增加，金属微粒表面电荷密度分布发生变化，导致受到向下的极化作用力。

3）电荷量减少和极化作用力向下共同导致覆膜后金属微粒的启举场强升高。

4）局部放电是覆膜后金属微粒的带电机理，随着SF6气体压力的增大，金属微粒发生局部放电的起始场强增大，启举场强升高。

[1] 乔胜亚, 周文俊, 唐念, 等. 不同吸附剂对GIS局部放电特征气体变化规律的影响[J]. 电工技术学报, 2016, 31(3)： 113-120. Qiao Shengya, Zhou Wenjun, Tang Nian, et al. Effects of different adsorbents on the evolving law of target gases under partial discharges in GIS[J]. Transactions of China Electrotechnical Society, 2016, 31(3)： 113-120.

[2] 季洪鑫, 李成榕, 庞志开, 等. 电压波形对GIS自由金属颗粒放电特性的影响[J]. 电工技术学报, 2016, 31(13)： 218-226. Ji Hongxin, Li Chengrong, Pang Zhikai, et al.Influence of voltage waveforms on partial discharge characteristics of GIS mobilized metal particles[J]. Transactions of China Electrotechnical Society, 2016, 31(13)： 218-226.

[3] Hama H, Okabe S. Factors dominating dielectric performance of real-size gas insulated system and their measures by dielectric coatings in SF6and potential gases[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(5)： 1737-1748.

[4] Srivastava K D, Tan M H E, Jaksts A, et al. Effect of dielectric coatings on metallic particle movement in compressed sulphur hexafluoride gas[C]//Annual Report, Conference on Electrical Insulation and Dielectric Phenomena, 1977： 448-455.

[5] Hama H, Inami K, Yoshimura M, et al. Dielectric properties of gas insulated bus applying low SF6 content and highly compressed N2/SF6gas mixtures[M]. New York： Gaseous Dielectrics IX, Springer US, 2001.

[6] Ooishi T, Hama H, Yoshimura M, et al. Charging mechanisms of a conducting particle on dielectric coated electrode in SF6gas[J]. Transactions Institute of Electrical Engineers of Japan, 1995, 115(6)： 485-491.

[7] 王健, 李庆民, 李伯涛, 等. 直流应力下电极表面覆膜对金属微粒启举的影响机理研究[J]. 电工技术学报, 2015, 30(5)： 119-127. Wang Jian, Li Qingmin, Li Botao, et al. Mechanism analysis of the electrode-coating's impact on the particle-lifting under DC voltage[J]. Transactions of China Electrotechnical Society, 2015, 30(5)： 119-127.

[8] Sakai K, Abella D L, Suehiro J, et al. Charging and behavior of a spherically conducting particle on a dielectrically coated electrode in the presence of electrical gradient force in atmospheric air[J]. IEEE Tansactions on Dielectrics and Electrical Insulation, 2002, 9(4)： 577-588.

[9] 张乔根, 贾江波, 杨兰均, 等. 气体绝缘系统电极表面覆膜时金属导电微粒带电原因分析[J]. 西安交通大学学报, 2004, 38(12)： 1287-1291. Zhang Qiaogen, Jia Jiangbo, Yang Lanjun, et al. Charging mechanism of metallic conducting particle on a dielectrically coated electrode in gas insulated system[J]. Journal of Xi'an Jiaotong University, 2004, 38(12)： 1287-1291.

[10] 王健, 李庆民, 李伯涛, 等. 考虑非弹性随机碰撞与SF6/N2混合气体影响的直流GIL球形金属微粒运动行为研究[J]. 中国电机工程学报, 2015, 35(15)：3971-3978. Wang Jian, Li Qingmin, Li Botao, et al. Motion analysis of spherical conducting particle in DC GIL considering the influence of inelastic random collisions and SF6/N2gaseous mixture[J]. Proceedings of the CSEE, 2015, 35(15)： 3971-3978.

[11] 邢藏菊, 王守觉, 邓浩江, 等. 一种基于极值中值的新型滤波算法[J]. 中国图象图形学报, 2001, 6(6)：533-536. Xing Cangju, Wang Shoujue, Deng Haojiang, et al. A new filtering algorithm based on extremism and median value[J]. Journal of Image and Graphics, 2001, 6(6)： 533-536.

[12] 卢章平, 孔德飞, 李小蕾, 等. 背景差分与三帧差分结合的运动目标检测算法[J]. 计算机测量与控制, 2013, 21(12)： 3315-3318. Lu Zhangping, Kong Defei, Li Xiaolei, et al. A method for moving object detection based on background subtraction and three frame differencing[J]. Computer Measurement & Control, 2013, 21(12)：3315-3318.

[13] 陈虎, 周朝辉, 王守尊. 基于数学形态学的图像去噪方法研究[J]. 工程图学学报, 2004, 25(2)： 116-119. Chen Hu, Zhou Zhaohui, Wang Shouzun. Research based on mathematics morphology image chirp method[J]. Journal of Engineering Graphics, 2004, 25(2)： 116-119.

[14] Savitzky A, Golay M J E. Smoothing and differentiation of data by simplified least squares procedures[J]. Analytical Chemistry, 1964, 36(8)：1627-1639.

[15] Pérez A T. Charge and force on a conducting sphere between two parallel electrodes[J]. Journal of Electrostatics, 2002, 56(2)： 199-217.

[16] Nojima K, Zhang Xueqin, Matsuzaki H, et al. Suppression of metallic particle lift-off in GIS by a nonlinear resistivity coating[J]. Electrical Engineering in Japan, 2014, 188(1)： 27-35.

[17] Parekh H, Srivastava K D, Van Heeswijk R G. Lifting field of free conducting particles in compressed SF6with dielectric coated electrodes[J]. IEEE Transactions on Power Apparatus and Systems, 1979(3)：748-758.

[18] Hornfeldt S P. Lifting force on metallic particles in gis systems[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2006, 13(4)： 838-841.

[19] Feng J Q, Hays D A. Electric field detachment of a uniformly charged dielectric sphere on a dielectric coated electrode[C]//Conference Record-IAS Annual Meeting (IEEE Industry Applications Society), 1996, 4： 1883-1890.

[20] Morcos M M, Zhang S, Srivastava K D, et al. Dynamics of metallic particle contaminants in GIS with dielectric coated electrodes[J]. IEEE Transactions on Power Delivery, 2000, 15(2)： 455-460.

[21] Ooishi T, Yoshimura M, Hama H, et al. Charging mechanisms of a conducting particle on dielectric coated electrode at AC and DC electric Fields[M]. New York： Gaseous Dielectrics VII. Springer US, 1994： 585-591.

[22] Prakash K S, Srivastava K D, Morcos M M. Movement of particles in compressed SF6GIS with dielectric coated enclosure[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1997, 4(3)：344-347.

[23] Niemeyer L. A generalized approach to partial discharge modeling[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1995, 2(4)： 510-528.

[24] Seeger M, Clemen M. Partial discharges and breakdown in SF6in the pressure range 25-150kPa in non-uniform background fields[J]. Journal of Physics D： Applied Physics, 2013, 47(2)： 202-215.

[25] Berger S. Onset or breakdown voltage reduction by electrode surface roughness in air and SF6[J]. IEEE Transactions on Power Apparatus and Systems, 1976, 95(4)： 1073-1079.

[26] Eriksson G. Easy evaluation of streamer discharge criteria[C]//Proceedings of 2012 COMSOL Conference, 2012.

[27] Parekh H, Srivastava K D. Effect of avalanche space charge field on the calculation of corona onset voltage[J]. IEEE Transactions on Electrical Insulation, 1979, 14(4)： 181-192.

（编辑 赫 蕾）

Influence Mechanism of Dielectric Coated Electrodes on Metallic Particle Lift-Off in SF6Gas under DC Voltage

Lü Fangcheng1Liu Hongyu1Li Zhibing2Dong Meng1Yan Xianglian2
（1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Beijing 102206 China 2. China Electric Power Research Institute Beijing 100085 China）

In order to study the influence mechanism of dielectrically coated electrode in SF6gas under DC electric field on metallic particle lift-off, experimental platform was setup and motion trajectory was recorded by high-speed camera. The experiment results showed that with the increasing of SF6gas pressures, the lift-off field of metallic particle was increased and the time to reach the high-voltage electrode was shortened. Instantaneous displacement of metallic particle was gained on the basis of image processing and computational method of charge quantity was raised on the combination of dynamics equation and least square method，analyzing of charge quantity showed that the metallic particle’s charge quantity decreased. Meanwhile, theoretical analysis model of field distribution around metallic particle under dielectric coated electrode was established, analyzing of electric field indicated that there was a enhance of electric field between coating and metallic particle and a transform of charge density distribution, which leaded to a downward polarization force formetallic particle. Both the decreasing of the electric charge quantity and the downward polarization force result in the increasing of lift-off field. On the whole, this article maintains that partial discharge is the charging mechanism of metallic particle; the enlargement of SF6gas pressure brings about the raise of initial electric field of partial discharge, causing the increase of downward polarization force with higher electric field to lift-off.

DC voltage, SF6gas, dielectric coated electrodes, electric charge quantity, polarization force, metallic particle lift-off

TM75

律方成 男，1963年生，博士，教授，博士生导师，研究方向为高电压与绝缘技术。

E-mail： lfc0818@sohu.com

刘宏宇 男，1990年生，博士研究生，研究方向为特高压GIL中金属微粒的运动及控制技术。

E-mail： lhy3120@126.com（通信作者）

10.19595/j.cnki.1000-6753.tces.161906

国家电网公司科技项目资助（GY71-16-070）。

2016-12-01 改稿日期 2017-03-19