某转子系统初始弯曲故障诊断的模糊专家系统

谢海鸿，王宇华

（1.佛山科学技术学院电子信息工程系，广东佛山528000；2.佛山科学技术学院机电工程系，广东佛山528000）

某转子系统初始弯曲故障诊断的模糊专家系统

谢海鸿1，王宇华2

（1.佛山科学技术学院电子信息工程系，广东佛山528000；2.佛山科学技术学院机电工程系，广东佛山528000）

以模糊数学理论为基础，提出了一个用于某转子系统初始弯曲故障诊断的模糊专家系统。利用隶属度和模糊综合评判的概念和方法有效地处理了领域知识描述和诊断推理中的不确定性问题。指出了在模糊推理模型中，模糊诊断权矩阵是专家诊断知识和诊断经验的集中体现，并且给出了确定的初始权矩阵的方法。

模糊理论；专家系统；故障诊断；权矩阵

专家系统作为一种热门技术在机械故障、电力系统故障、发动机转子等各种故障诊断中逐渐得到应用，这种方法的新颖、高效、快速，但在故障诊断中也遇到一些麻烦。因为发动机转子故障复杂、多样，故障与正常之间的界限并不一定很明确，加上现有数据采集过程中的缺陷，造成了许多棘手的问题。本文运用模糊数学推出有效的诊断方法。

1 某转子系统故障机理的数学描述

某转子系统故障包括初弯、不平衡、不对中、碰磨等，其故障形式和故障征兆之间的关系是随机和模糊的。为此，本文基于模糊语言值逻辑，给出用于故障诊断的模糊关系矩阵的概念。设X、Y分别是该转子系统的故障征兆和故障原因的集合，分别表示为

式中，m与n分别为故障原因、故障征兆的总数，取n=11，m=4；x1为波形（人机对话）；x2为轴心轨迹（人机对话）；x3为振幅随转速增大而增大的程度（人机对话）；x4为在低速区转子随转速增大而减小的程度；x5为0.5f1；x6为（0.5～0.8）f1；x7为f1（基频）；x8为2f1（2倍频）；x9为3f1（3倍频）；x10为4f1（4倍频）；x11（5～16）f1（5～16倍频）；y1为不平衡；y2为初弯；y3为非对中；y4为碰摩［1］。

故障原因和故障征兆之间的模糊关系矩阵R可表示为

1.1 故障征兆隶属度的确定

将故障征兆集X=｛x1，x2，…x11｝按属性划分成s个子集，有Xi=｛xi1，xi2，…xikl｝，

1.1.1 人机对话的故障征兆隶属度的确定

以故障征兆波形为例，语言变量值X1为波形，波形=｛正弦波，正弦波含2倍频，正弦波含等距离脉冲，自激振荡｝，即X1=｛x11，x12，x13，x14｝。

由于各种征兆对转子不同故障的征兆的隶属度不同，因此引入权重因子［2-3］，即

于是可以确定人机对话的故障征兆隶属度，当xi中的某元素xij出现时，xij取1，否则取0。有

1.1.2 可测量值故障征兆隶属度的确定

可测量值故障征兆隶属度［4］可按

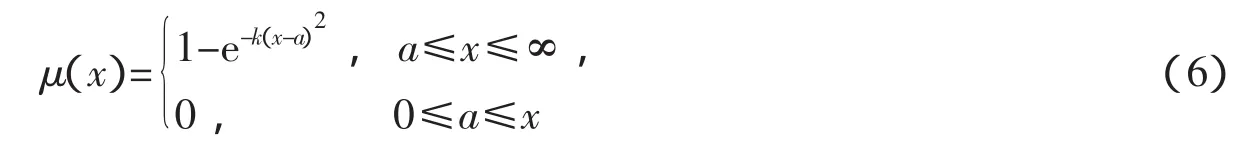
确定。其中，a为允许故障频率在差异的范围内，其取值要根据各种特征频率而确定。

1.2 模糊关系矩阵的确定

由式（3）可知，将故障征兆划分成4个故障子集。若为单因数矩阵，则得出一级评判向量，即

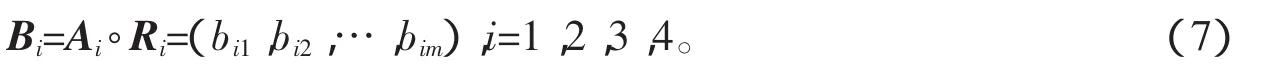
将每个Xi视为一个因数，记X=｛X1，X2，X3，X4｝，这样X又是一个因数集，其单因数确定矩阵为

每一个Xi作为X的一部分，反映了X某种属性，可以按它们的重要性给出权重分配A=（a1，a2，…，as）。于是得到二级评判向量B=A◦R=（b1，b2，…，bm）。其二级评判模型［5］如图1所示。

权重因子aij的赋值由大量的实验统计数据及专家经验而定。如果用数值表示，则取aij∈［0，1］，其中aij=0，表示yi不可能导致xi出现；aij= 1,表示yi必然导致xi出现；aij约接近1，表示导致出现的可能性越大，反之，则越小。

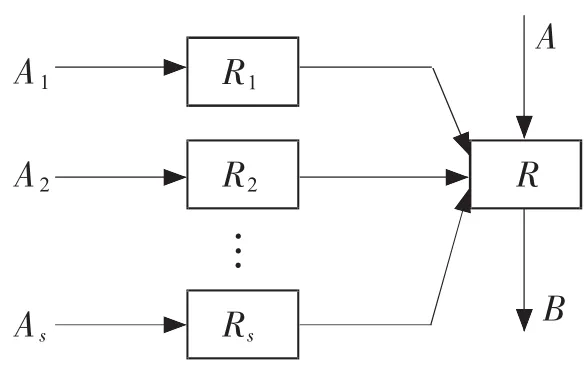
图1 二级评判模型

2 实际应用

本研究应用模糊理论对该转子系统进行故障测试。

系统主要参数包括：转轴长度为0.56 m，轮盘质量为0.116 36 kg，转轴截面刚度为1.01×104 Nm2，阻尼系数为7.06 kg/s，刚度系数为2.814×106 N/m，临界转速为5 200 r/min，小偏心为1.786 5×10-5（16 gcm），大偏心为4.466 2×10-5（40 gcm）。

该转子系统经过了约1万余次升速及降速通过临界转速的实验，转子产生了剩余弯曲，即在静止状态时，轮盘处转轴具有0.002 cm的初始弯曲，其初弯特性实验曲线如图2所示。

图2 初弯特性实验曲线（波特图）

2.1 隶属度函数的确定

2.1.1 μ（x1）、μ（x2）、μ（x3）的确定

x1，x2，x3的隶属度μ（x1）、μ（x2）、μ（x3）均按式（5）确定（一级评判参数略）。

2.1.2 μ（x4）的确定

（1）当不平衡度为0 gcm时，Amin=20（RMS），Xmin=∞。（2）当不平衡度为16 gcm时，Amin=9.2（RMS），Xmin=3 900 r/min。（3）当不平衡度为40 gcm时，Amin=4.09（RMS），Xmin=3 500 r/min。Amin表示振幅的最小值，Xmin表示振幅取最小值时的速度。当Amin=

20时，μ（Amin）=0.0；当Amin=5时，μ（Amin）=0.5。

利用式（6），取a=20，则k=1/350，所求出μ（x4）的隶属度如表1所示。

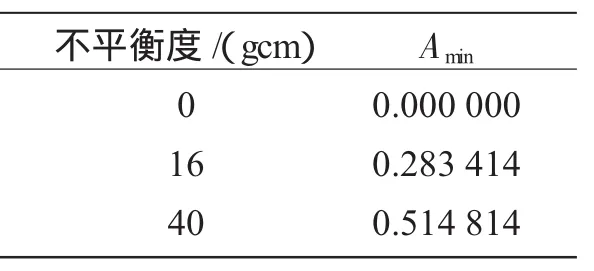
表1 μ（x4）的隶属值

2.1.3 各功率谱的隶属度的确定

根据图2的功率谱测量，可以得到功率谱值，如表2所示。

表2 功率谱值

同理，根据式（6），取a=1 280，k=1/40 000，可求解出1倍频的隶属度μ（x7）；取a=95，k=0.000 5，可求解出2倍频的隶属度 μ（x8）；取a=40，k=0.002，可求解出3倍频的隶属度μ（x9）；取a=60，k=0.002，可求解出4倍频的隶属度μ（x10）。由此得出X4子集中各元数的隶属度，如表3所示。

表3 X4子集中各元数的隶属度表

2.2 模糊关系矩阵

单因数模糊关系矩阵利用经验给出波形，轴心轨迹等各故障征兆对故障现象的隶属度（此处省略）。

2.2.1 多因数模糊关系矩阵

多因数模糊关系矩阵利用经验和统计数据得出，其关系矩阵如表4所示。

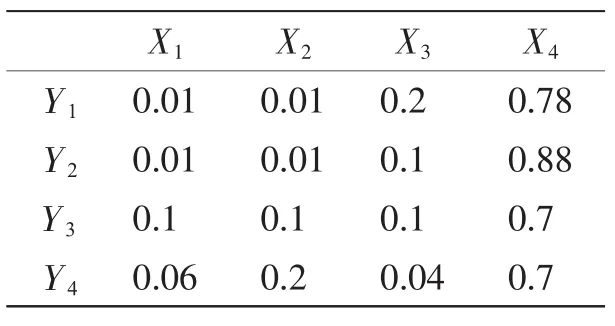
表4 二级评判模糊关系矩阵

2.2.3 发动机转子的故障征兆

发动机转子的故障征兆包括转子不平衡、初弯、不对中、碰摩4种情况，其故障征兆如表5所示。

表5 发动机转子故障征兆

利用式（2）可以计算出各故障形式的隶属度，如表6所示。

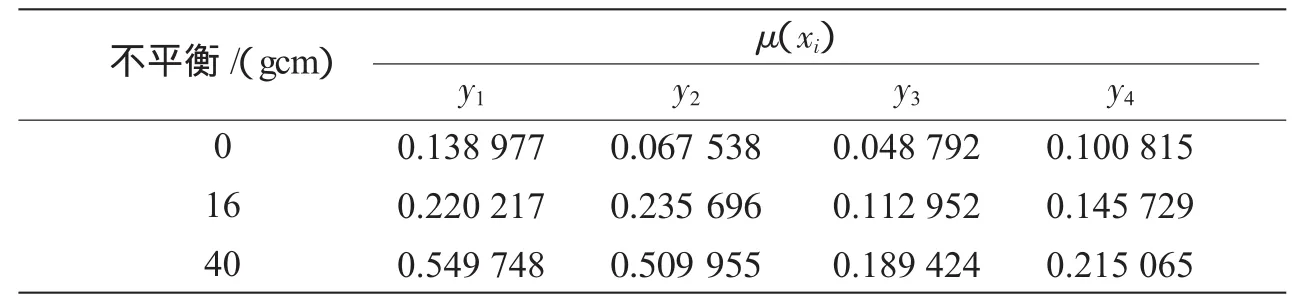
表6 故障形式的隶属度μ（xi）

从表6可以看出，当不平衡度为0 gcm时，故障隶属度不为0，表示存在残留不平衡度，随着不平衡度的增加，初始弯曲和不平衡都会随之增加［6］。

3 小结

本方法建立的故障诊断系统，在某转子系统故障诊断中得到了很好的验证。若对诊断方程进一步完善，则可以建立故障检测模糊专家系统。因此，此方法对转子的故障检测自动化有使用价值。

［1］虞和济,韩庆大,李沈,等.设备故障诊断工程［M］.北京:冶金工业出版社,2001.

［2］朱剑英.智能系统非经典数学方法［M］.武汉:华中科技大学出版社,2001.

［3］彭祖赠,孙韫玉.模糊数学及其应用［M］.武汉:武汉大学出版社,2002.

［4］梅胜敏,徐洪昌,张幼桢.故障诊断专家系统中的模糊推理方法［J］.南京航空航天大学学报,1995,27（4）:519-524.

［5］卫振华,忻建华,曹华.等基于隶属度和规则的层次分类诊断模型［J］.中国动力工程学报,2005,2（2）:258-261.

［6］周辉.iMEC系统及其在转子热弯曲故障诊断中的应用［J］.振动与冲击,2014,33（s）:578-582.

【责任编辑：任小平 renxp90@163.com】

Fuzzy reasoningmethod in expertsystem for faultdiagnosis

XIE Hai-hong1,WANG Yu-hua2
（1.Department of Electronics and Information Engineering，Foshan University,Foshan 528000,China；2.Department of Mechatronics Engineering,Foshan University,Foshan 528000,China）

This paper is about fuzzy reasoningmethod in expertsystem for one rotor faultdiagnosis.The concept and themethod ofmembership and fuzzy comprehensive judgements are used to dealwith the field knowledge description and the uncertain problem in diagnosing inference.Itwas pointed out that the fuzzy diagnosisweight matrix in the fuzzy diagnosismodelwas the concentrative reflection of the diagnosis knowledge and experiences of the human experts.At last,the algorithm to originally determine diagnosisweightmatrix isgiven.

fuzzy set theory;expertsystem;faultdiagnosis;weightmatrix

TM711.2

A

2017-03-03

广东省公益研究与能力建设专项资金项目资助（2015A010103017,2015B010101014）

谢海鸿（1962-），女，广东佛山人，佛山科学技术学院讲师。

1008-0171（2017）04-0059-04