基于VBA的高铁接触网整体吊弦计算
2017-07-18郭家祥王天龙
郭家祥,王天龙
基于VBA的高铁接触网整体吊弦计算
郭家祥,王天龙
弹性链形整体吊弦的计算是高速铁路接触网施工核心技术之一,本文对简单链形和弹性链形两大悬挂分类讨论,从模型建立、理论基础、计算式推导到结论得出整体吊弦详细的计算过程,最后根据得出的结论和计算式设计了相应计算软件。
整体吊弦;弹性链形悬挂;VBA
0 引言
随着我国铁路电气化的不断发展,高速已成为我国铁路的重要标志特征。越来越高的运行速度对接触网提出了更高的安全性、可靠性和平顺性要求。吊弦的计算精度决定了接触网的弹性和平顺性,是良好弓网关系的主要决定因素。国内高速铁路多采用弹性链形悬挂,部分采用简单链形悬挂。业内对弹性链形吊弦计算的研究和实践较少,高铁线路建设使用国外公司软件,收费高昂且受制于人。对弹性链形悬挂吊弦计算进行深入研究,研制出实用、易用的吊弦计算软件,以满足现实需求是很有必要的。
详尽研究不同悬挂方式吊弦长度的计算,并根据理论结果编制一个效率较高的计算软件是本文论述的主要内容。
1 总体方案
国内高铁接触网悬挂形式主要分为2大类:简单链形悬挂和弹性链形悬挂,以及需探讨的弹简链过渡跨。吊弦计算的本质是确立正确的计算模型和误差较小的力学分析。本文论述的2大悬挂形式都是基于抛物线模型。确定模型后利用力学理论对关键点和段进行受力分析进而得出基本公式,由于吊弦长度受诸多因素影响,所以对吊弦长度进行修正也是至关重要的步骤。基于本文所推导出来的理论公式进行软件设计,对测量数据进行提取加工并输出成为有意义的结果,且最大程度做到人性化和最优化。本文从简单链形悬挂吊弦计算、弹吊计算、弹性链形悬挂普通吊弦计算、弹简链过渡跨吊弦计算4个方面由简至深分析讨论,从基本长度计算式到因影响因素所做的修正再到最后的扣料输出作出详细论述,力求考虑周全。
2 简单链形悬挂吊弦计算
2.1 基本假设及模型
柔性架空接触网关于线索几何参数计算的理论都是建立在抛物线基础上的,并作如下假设:
(1)承力索和接触线均为两端固定且只承受重力作用的自由悬挂线索;
(2)线索柔软,无刚性;
(3)线索直径与其长度比可以不计,即细长比很大;
(4)悬挂自重均匀分布。
图1为抛物线模型图[1]。
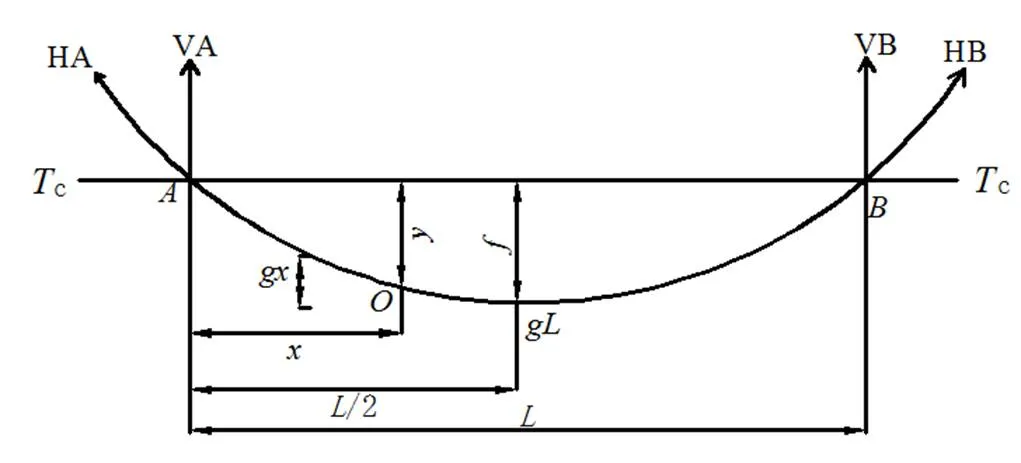
图1 承力索抛物线模型图
视承力索模型为抛物线,可得任意点弛度为
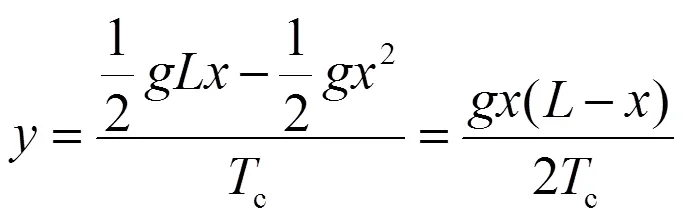
式中,为承力索当量线密度;c为承力索的给定张力值;为、两定位点间的跨距;为任意点吊弦距定位点距离。
由此建立简单链形悬挂吊弦计算模型如图2所示。
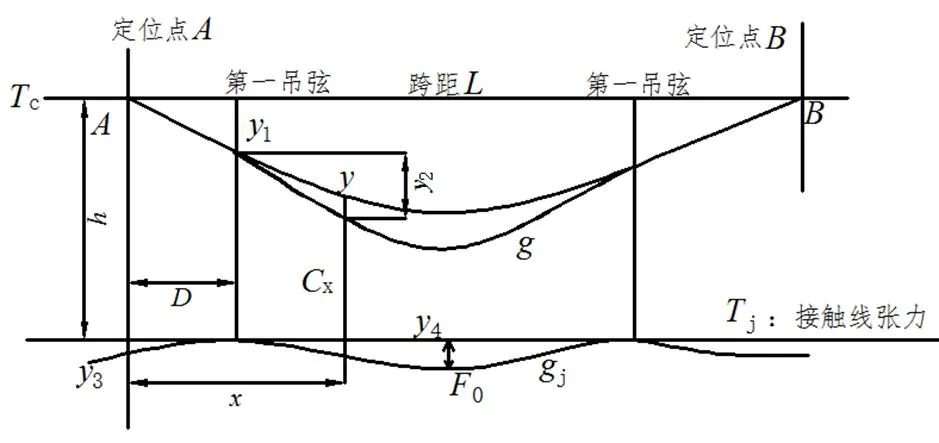
注:h为定位点的结构高度;D为第一根吊弦距定位点的距离;Tj为接触线的给定张力值;gj为接触线当量线密度;F0为接触线预弛度。
2.2 基本公式推导
由图2模型可推导出吊弦基本长度为
x=-1-2-3+4(2)
(1)承力索在支柱定位点左右第一吊弦处弛度为

(2)2个第一吊弦之间的承力索弛度为
(4)
(3)定位点左右第一吊弦间接触线弛度值为

(4)当接触线存在预弛度0时,计算点接触线的预弛度为
(6)
综上,各简单链形整体吊弦计算式为
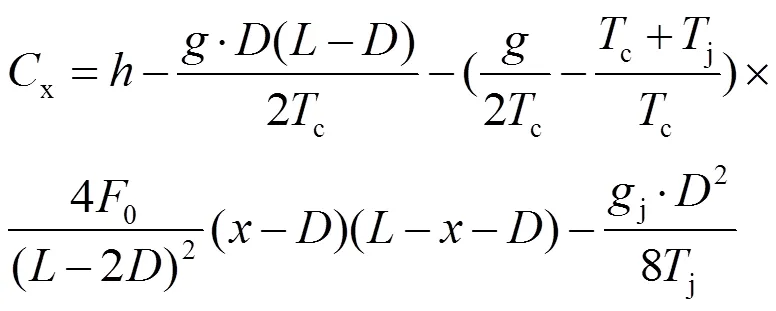
2.3 演化及调整
(1)承力索不等高悬挂,接触线高度相等时的吊弦长度计算方法和计算式与等高悬挂相同,只需用悬挂点的实际高度=1+ (2-1)/,替换式(7)中的即可。其中,1,2为两定位点的实际结构高度。
(2)两定位点导高不等时的不等高悬挂的吊弦长度与(1)中所述相同。
(3)有集中载荷的等高悬挂的吊弦长度为
V=·(-) /(≤≤)
V=·(-) /(<≤-) (8)
式中,为荷载质量;为荷载距第一定位点距离。
(4)吊弦长度的修正。
a.直线区段拉出值对吊弦长度影响可忽略不计,曲线区段主要考虑测量承高由拉出值和外轨超高带来的对低轨折算高度的影响。
曲线区段因外轨超高引起接触线与线路中心偏移,从而引起吊弦长度增加,其增加量为

式中,w为外轨超高值;为曲线半径。
b.因竖曲线引起的吊弦长度的修正。
竖曲线圆心在线路下方取正,在上方取负,竖曲线半径0,吊弦长度的增加量为
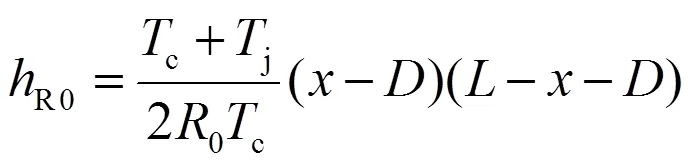
综上,可得吊弦理论长度d为
d=x+V-R-R0(11)
理论长度d考虑吊弦线夹的扣料和载流环的预留就可得到吊弦的实际下料长度。
3 弹性链形悬挂吊弦计算
3.1 基本假设及计算模型
(1)承力索、弹性吊索、接触线均为理想的柔软线索,只能承受沿其轴线方向的拉力。
(2)承力索沿方向的质量分布考虑弛度的影响,接触线沿方向的质量分布均匀,在受力分析时考虑其数值。
(3)每根吊弦的质量由2部分组成:固定质量和长度质量。固定质量包括吊弦的上下线夹、紧固螺栓、基本接头质量等。长度质量是随吊弦长度变化而改变的质量。
弹性链形悬挂基本模型如图3所示,定位点受力分析如图4所示。
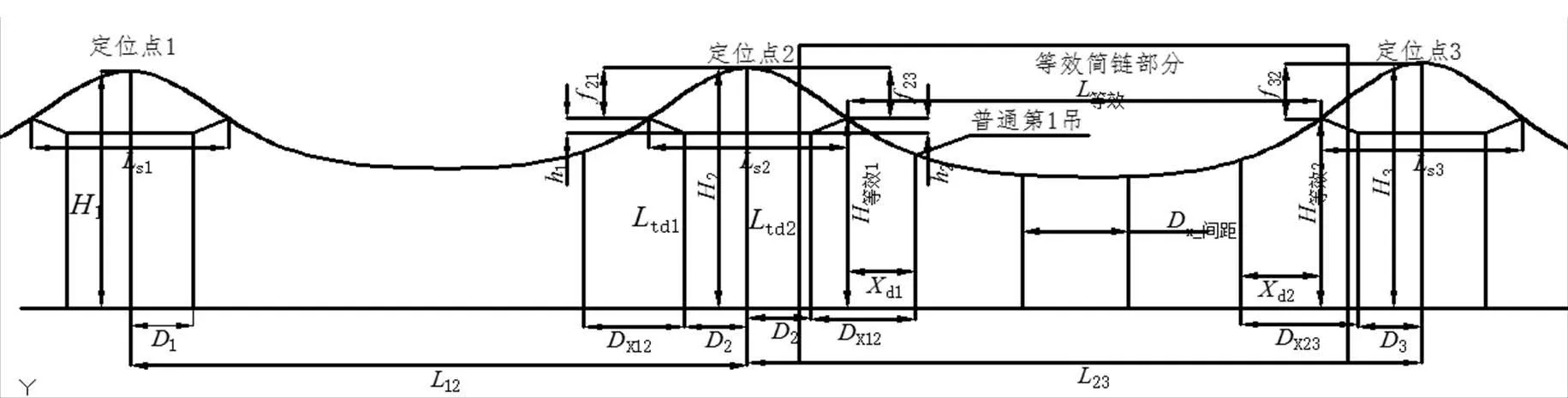
图3 弹性链形悬挂模型图
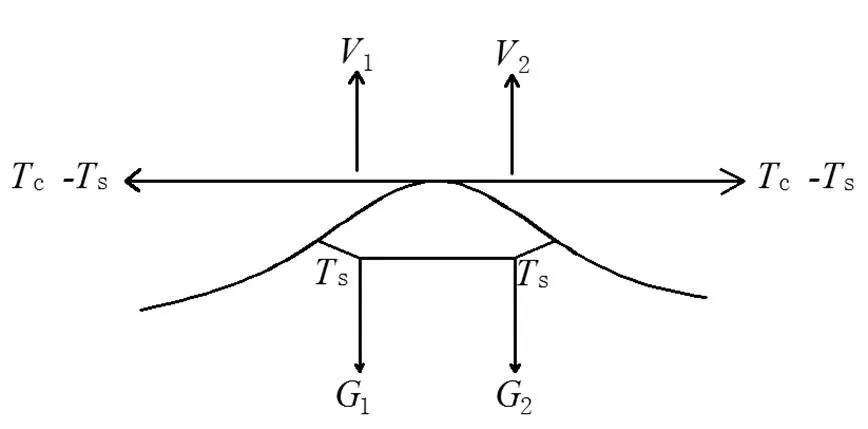
图4 定位点受力分析图
设定相邻2跨跨距分别为12,23,3个悬挂点的结构高度依次为1、2、3。弹性吊索的长度分别为s1、s2、s3。弹性吊弦距定位点的距离分别为1、2、3。普通第一吊弦距弹性吊弦距离为X。1、2分别为2个弹性吊弦的轴向力。21和23为定位点2处(弹性吊索在承力索上的安装位置)承力索的弛度。1和2为弹性吊弦处弹性吊索的弛度;c、s分别为承力索及弹性吊索的张力在水平方向上的分力,c、j、s、d分别为承力索、接触线、弹性吊索、吊弦均匀分布在承力索上的线密度,td为弹性吊弦重量。
3.2 弹性吊弦长度计算推导
对支柱2进行承力索受力分析,其支座反作用力由2部分构成:跨距12引起的反作用力、由跨距23引起的反作用力。2个力作用于承力索支座。在该点2个力分别决定两侧承力索弛度。
跨距23引起的支座反作用力1为
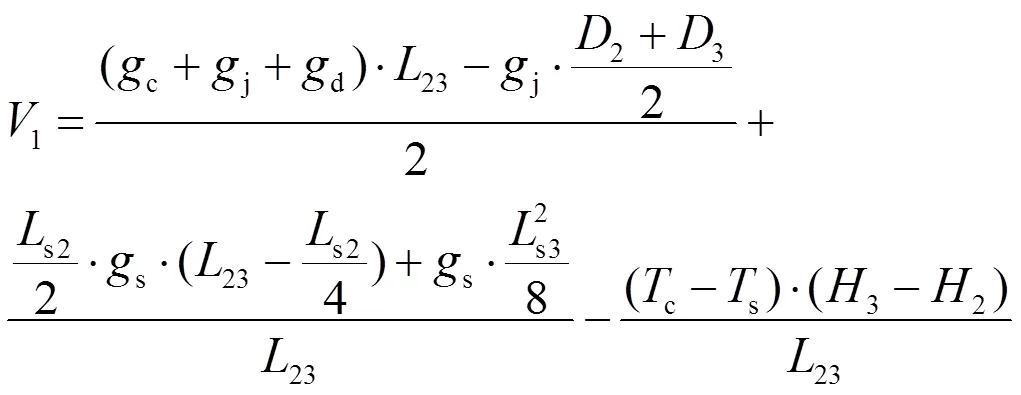
同理可得由跨距12引起的支座反作用力2为
(13)
定位点2处两侧承力索弛度为

(15)
定位点2处弹性吊弦1悬挂点重量1为
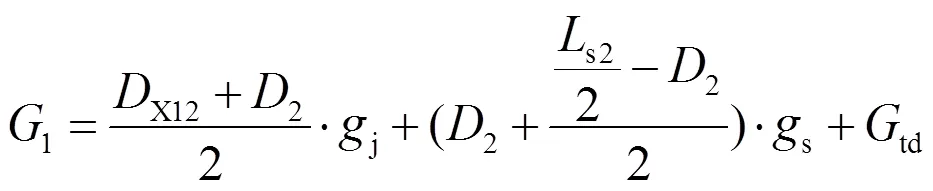
定位点2处弹性吊弦2悬挂点重量G2为
(17)
根据式(1),可求得弹性吊弦悬挂处弹性吊索的弛度:
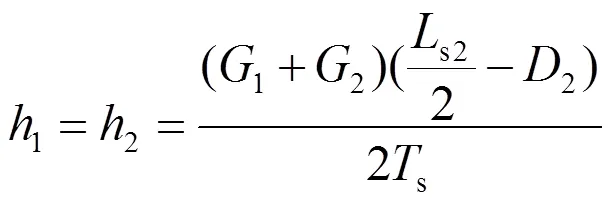
此时,可利用几何关系求得弹吊理论长度:
td1=2-21-1(19)
td2=2-23-2(20)
3.3 等效简链部分吊弦计算
由图3模型可类推计算得到每一个弹性链形悬挂下的弹性吊弦长度,此后图3中的普通吊弦可等效为简单链形悬挂计算,并且设定接触线预留弛度为0,其等效模型如图5所示。
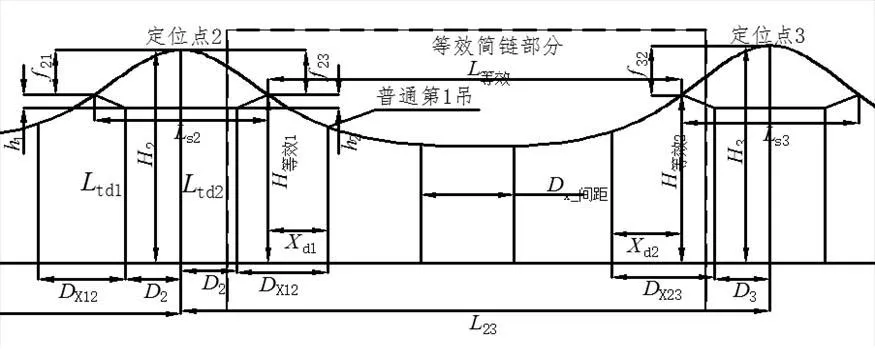
图5 简单链形悬挂等效模型图
由模型可知,等效简链部分的等效定位点为弹性吊索线夹处。
等效结构高度为
等效1=2-23(21)
同理可得
等效2=2-32(22)
其中,32计算方式同21
忽略弹性吊索弛度对其水平长度的影响,第一吊弦距等效定位点(吊索线夹)的距离为
d1=X12+2-(23)
d2=X23+3-(24)
等效跨距为
等效=23-(25)
吊弦数量由23决定,普通吊弦数量为总吊弦数减去该跨弹吊数(普通为2,过渡跨为1)。
吊弦间距为

由以上各式可求得任意吊弦距等效定位点距离,引用简链吊弦计算公式可求得普通吊弦长度
(27)
等效简链普通吊弦的修正可参考第2.3节所述的修正方法。
4 2种链形悬挂过渡跨吊弦计算
在锚段关节部分,需要从弹性链形悬挂过渡为简单链形悬挂,接触线经2次抬高后下锚,屋面形导线布置方式很好地解决了列车速度较高时受电弓从一个锚段过渡到另一个锚段时在传统的锚段关节中等高段接触压力变大,受流恶化的问题。为了能精确计算弹性链形悬挂锚段关节部分的整体吊弦,将2种悬挂模型进行合并演化[2]并做以下讨论。
图6为2种悬挂过渡跨示意图,设定跨距为,2个悬挂点结构高度为1,2,弹性吊索长度为s,弹性吊弦距悬挂点距离为1,普通吊弦距弹吊距离为X1,2为吊索线夹处承力索弛度,2为弹性吊弦处弹性吊索的弛度。
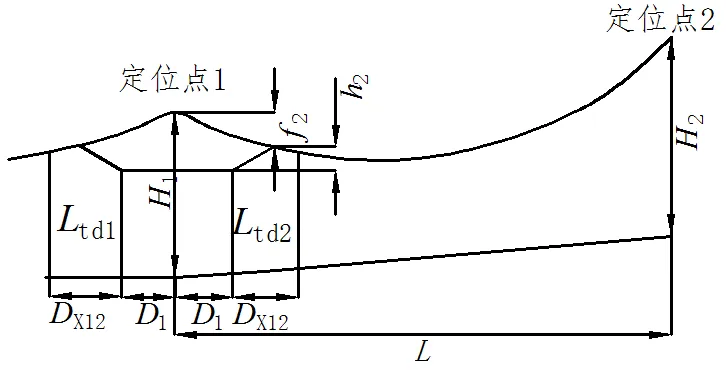
图6 简单链形悬挂与弹性链形悬挂过渡图
结合图6,对该跨进行受力分析,可得计算跨距引起的支座反作用力为

由此求得吊索线夹处承力索弛度为
(29)
弹吊1悬挂点处轴向力1为
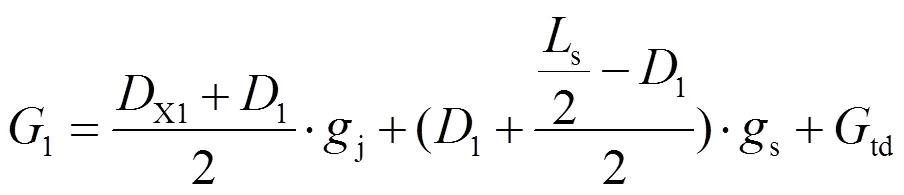
由于接触线抛物线的存在,接触线自重传递给承力索上的线密度会减小,但其造成的影响可忽略不计。故弹吊2悬挂点处轴向力2=1。
由此得到弹性吊索弛度为

综上可得弹性吊弦2长度为
td2=1-2-2(32)
弹性吊弦1的计算与普通弹性链形悬挂的计算方式一致,事实上,假设悬挂点2处也为弹性链形悬挂,并且设定其吊索长度为0,按照弹性链形悬挂的计算方法,所有计算式中的s3、3均设定为0,推导出的结果与本节结论一致。
同弹链跨中吊弦等效为简链模式一样,将从吊索线夹到定位点2之间的部分仍等效为简单链形悬挂,与弹链跨中等效模型不同的地方是第2定位点为实际悬挂,不是等效到吊索线夹上。
5 吊弦计算软件的设计
在第2—第4节中,详细介绍了不同悬挂方式下吊弦的计算过程和计算式。本节主要讨论如何利用得到的理论计算式结合VBA编程语言,设计一款简单高效的吊弦计算软件。
5.1 VBA简介
Visual Basic for Applications(VBA)是Visual Basic的一种宏语言,是微软公司开发的在其桌面应用程序中执行的通用自动化(OLE)任务编程语言。其主要功能是扩展Windows的应用程式,特别是Microsoft Office软件,也可说是一种应用程式视觉化的Basic 脚本。Excel中利用VBA编程可省去单元格中复杂的引用和公式,又结合了Excel输入便捷的优点,使得自动化作业变得简洁高效。
5.2 整体框架
软件采用Excel+VBA编程,Excel界面设有“参数设置”“数据输入”“吊弦布置”“吊弦长度”“下料长度”等项。其中“参数设置”用来设置不同线路的给定设计常量,包括线材张力及密度,线夹尺寸等参数。“数据输入”用来采集吊弦计算所必须的测量数据,包括承导高度、线路信息、集中荷载信息。“吊弦布置”为计算结果一项,用以向现场安装人员提供吊弦的安装位置。“吊弦长度”为计算吊弦理论长度。“下料长度”为计算结果一项,用以向吊弦预制人员提供预制基础数据。
5.3 数据输入
计算者需在数据输入模块录入计算的原始测量数据,例如承导高度,若为曲线,还需录入曲线信息及测量拉出值,以便对承导高度进行转换。值得注意的是,计算者需正确录入当前定位点的悬挂方式,该项用3个大写字母表示,用来告知软件当前定位点及相邻两定位点的悬挂方式,使得软件做出识别并引用相应的计算模块。
5.4 VBA整体流程
如图7所示,软件主体流程为一个判断语句,并根据不同的悬挂形式跳转到相应的计算模块。
5.5 计算
VBA中,不同的模块均使用相同的流程,即从输入数据表中提取计算所用数据,然后按照第2—第4节中的计算式进行计算,最后将计算结果输出到“吊弦布置”及“吊弦长度”表中,图8为截取的弹吊计算过程VBA源代码。

01.h1 = Sheets("输入数据").Range("B" & DX_bianhao - 1) - Sheets("输入数据").Range("D" & DX_bianhao - 1) 02.h2 = Sheets("输入数据").Range("B" & DX_bianhao) - Sheets("输入数据").Range("D" & DX_bianhao) 03.h3 = Sheets("输入数据").Range("B" & DX_bianhao + 1) - Sheets("输入数据").Range("D" & DX_bianhao + 1) 04.Ts = Sheets("输入数据").Range("M" & DX_bianhao) '提取吊索张力 05.V1 = ((Gc + Gj + Gd) * 9.8 * L2_3 - Gj * 9.8 * (D2 + D3) / 2) / 2 + (Ls2 / 2 * Gs * 9.8 * (L2_3 - Ls2 / 4) + Gs * 9.8 * Ls3 * Ls3 / 8) / L2_3 - (Tc - Ts) * (h3 - h2) / (1000 * L2_3) 06.V2 = ((Gc + Gj + Gd) * 9.8 * L1_2 - Gj * 9.8 * (D1 + D2) / 2) / 2 + (Ls2 / 2 * Gs * 9.8 * (L1_2 - Ls2 / 4) + Gs * 9.8 * Ls1 * Ls1 / 8) / L1_2 - (Tc - Ts) * (h2 - h1) / (1000 * L1_2) 07.f21 = (V2 * Ls2 - Ls2 * Ls2 * Gc * 9.8 / 4) / (2 * (Tc - Ts)) 08.f23 = (V1 * Ls2 - Ls2 * Ls2 * Gc * 9.8 / 4) / (2 * (Tc - Ts)) 09.G1 = (DX12 + D2) * Gj * 9.8 / 2 + (D2 + (Ls2 / 2 - D2) / 2) * Gs * 9.8 + Gd * 9.8 10.G2 = (DX23 + D2) * Gj * 9.8 / 2 + (D2 + (Ls2 / 2 - D2) / 2) * Gs * 9.8 + Gd * 9.8 11.htd = (G1 + G2) * (Ls2 / 2 - D2) / (2 * Ts) 12.Ltd1 = h2 - f21 - htd '弹吊1长度 13.Ltd2 = h2 - f23 - htd '弹吊2长度
6 结语
本文从简单链形悬挂吊弦计算、弹吊计算、弹性链形悬挂普通吊弦计算、弹简过渡跨吊弦计算4个方面入手,通过建立模型、选定理论、推导计算式得出结论,详细论述了吊弦长度的计算过程并设计了相应计算软件。该软件在多条线路中与西门子软件对比验证,计算结果能够满足设计要求和施工误差。但是国内吊弦计算的方法还有很大的待研究空间,比如张力差因素、竖曲线因素的精确数学模型确定等,还有很多方面需要设计研究人员继续探索和研究。
[1] 董昭德. 普通高等教育铁道部规划教材[M]. 北京:中国铁道出版社,2010.
[2] 纪小军. 弹性链形悬挂锚段关节过渡跨吊弦长度的计算[J]. 电气化铁道,2005,(4):32-33.
The calculation of integral droppers for stitched catenary suspension is one of key technologies for construction of overhead contact system of high speed railways, the paper analyzes the two suspension types by classification of simple catenary and stitched suspension, and the detailed calculation process of integral droppers are obtained by establishment of models, derivation of theories and formulae; the related calculation software is designed on the basis of obtained conclusion and formulae.
Integral droppers; stitched catenary suspension; VBA
U225.4+8
B
1007-936X(2017)03-0053-06
2016-08-10
郭家祥.中铁建电气化局集团第三工程有限公司,工程师,电话:18519501988;王天龙.中铁建电气化局集团第三工程有限公司,助理工程师。
