双指标非交换鞅的一些不等式

尹 磾,马聪变

(武汉大学数学与统计学院,湖北武汉 430072)

双指标非交换鞅的一些不等式

尹 磾,马聪变

(武汉大学数学与统计学院,湖北武汉 430072)

本文研究了双指标非交换鞅的一些不等式问题.利用单指标非交换鞅不等式的方法,获得了双指标非交换鞅的‖·‖Hp(M)和‖·‖hp(M)之间的关系(2≤p＜∞).推广了双指标非交换鞅的‖·‖Lp(M)和‖·‖hp(M)之间的等价关系(2≤p≤4).

von Neumann代数;双指标鞅;Burkholder不等式;鞅Hardy空间

1 引言

非交换鞅空间理论是非交换数学中分析理论的有机组成部分,是当前泛函分析领域的前沿研究方向.从20世纪70年代,人们开始研究非交换鞅.为了研究非交换鞅空间,需要引进新的思想和方法.1971年Cuculescu[1]研究了非交换鞅的弱(1,1)型不等式并提出了著名Cuculescu构造以取代停时的方法.1997年Pisier和Xu[2]取得重大突破,他通过引进列均方函数与行均方函数对p＜2与p≥2分别定义了恰当的非交换鞅的Hardy空间Hp(M),并由此证明Burkholder-Gundy鞅不等式的非交换类比.随后经过众多数学家的努力,非交换鞅取得重要进展.到目前为止,绝大多数经典鞅的不等式都成功过渡到了非交换情形,例如条件均方函数的Burkholder不等式[3],Doob极大不等式[4],Stein不等式[2]等.

双指标鞅是单指标鞅的自然推广.在交换的情形,Weisz对双指标鞅做了许多工作(见文[5]).Weisz的工作表明,从单指标到双指标绝不是简单的推广,实际上很多在单指标鞅研究中常用的方法不能够适用于双指标鞅的情形.因此常常需要一些新的技巧和方法.

关于双指标非交换鞅的研究目前尚属起步阶段.本文研究双指标非交换鞅,证明了双指标非交换鞅的一些不等式.包括双指标非交换鞅的‖·‖Hp(M)和‖·‖hp(M)之间的关系,双指标非交换序列的Stein不等式以及‖·‖Lp(M)和‖·‖hp(M)之间的等价关系.

2 定义与记号

首先回顾一下关于非交换Lp-空间的一些基本定义与记号.设(M,τ)是一个非交换概率空间,这里M是Hilbert空间H上的von Neumann代数,τ为M上的正规忠实的迹,满足τ(1)=1.记L0(M)为关于(M,τ)的可测算子全体组成的拓扑∗-代数.设1≤p＜∞,令

则(Lp(M),‖·‖p)是Banach空间,称之为关于(M,τ)的非交换Lp-空间.当p=∞时,规定L∞(M)=M,且L∞(M)上的范数‖·‖∞为算子范数.设(Mn)n≥0是M的一列单调增加的子von Neumann代数,用En表示M到Mn的条件期望算子.Lp(M)中的序列x=(xn)n≥0称为是关于(Mn)n≥0的鞅,若对任意的m≥n,有En(xm)=xn.关于非交换Lp-空间与非交换鞅的更详细的介绍可参见文献[6].

设N是非负整数的集合,N2={ (n1,n2)：n1,n2∈N}.在N2上定义半序如下：对任意的n=(n1,n2),m=(m1,m2)∈N2,定义n≤m当且仅当n1≤m1,n2≤m2以及n＜m若n≤m且n/m.设(Mn;n∈N2)是M的一列关于N2偏序单调增加的子von Neumann代数,并且在M中w∗-稠密.对任意的n=(n1,n2)∈N2,用En或者En1,n2表示M到Mn的条件期望算子.一般地,对于M的任意一列子von Neumann代数(Nn;n≥0),令表示包含的最小的von Neumann代数.对每个(n1,n2)∈N2,定义

以后总是设(Mn;n∈N2)满足(F4)条件：对任意的x∈M和任意的n=(n1,n2)∈N2,有

为了方便起见,规定对任意的x∈L1(M),当n1=0或者n2=0时,En1,n2(x)=0.

定义2.1设x=(xn,n∈N2)是L1(M)中的序列.称x为关于(Mn)n∈N2的鞅,如果满足

若进一步对每个n∈N2,有xn∈Lp(M)(1≤p≤∞),则称x为关于(Mn)n∈N2的Lp-鞅.此时,令

若‖x‖p＜∞,则称x为Lp-有界鞅.

设x=(xn,n∈N2)是关于(Mn)n∈N2的鞅,n=(n1,n2).令

约定当n1=0或者n2=0时,dxn=0,称dx=(dxn)为x的鞅差序列.容易证明当(Mn)n∈N2满足(F4)条件时,若(dxn,n∈N2)是鞅差序列,则En(dxm)=0(∀nm).

为了定义关于双指标非交换鞅的Hardy空间,先回顾一下非交换列空间与行空间的定义(详见文[6]).

设1≤p＜∞,x=(xn)是Lp(M)中的有限序列.令

则‖·‖Lp(M,lc2)和‖·‖Lp(M,lr2)在Lp(M)的有限序列上定义了范数.相应的完备化空间分别记为.注意到对于Lp(M)中的一个序列(xn),如果在Lp(M)中有界,则极限存在.用表示这个极限,则

当1≤p＜∞时,CRp[Lp(M)]空间定义如下.

(i)当p≥2时,定义,赋予范数

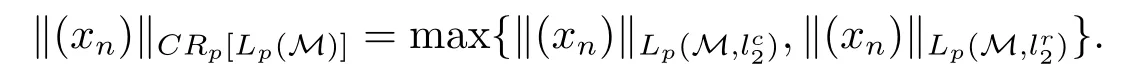
(ii)当1≤p＜2时,定义,赋予范数

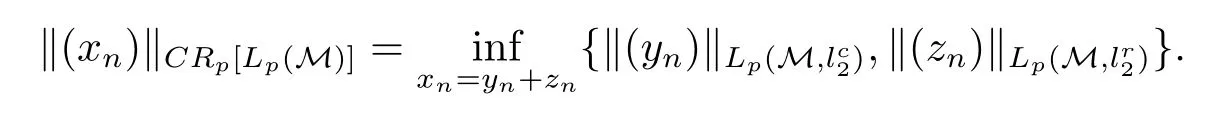
下面定义双指标非交换鞅的Hardy空间Hp(M).设x=(xn,n∈N2)是一个鞅,令

如果(Sc,(n,n)(x))n≥1和(Sr,(n,n)(x))n≥1在Lp(M)中有界,令

称Sc(x)和Sr(x)分别为鞅x=(xn,n∈N2)的列均方函数与行均方函数.

定义2.2(i)设1≤p＜∞.定义双指标非交换鞅的列Hardy空间,

类似地,定义双指标非交换鞅的行Hardy空间.

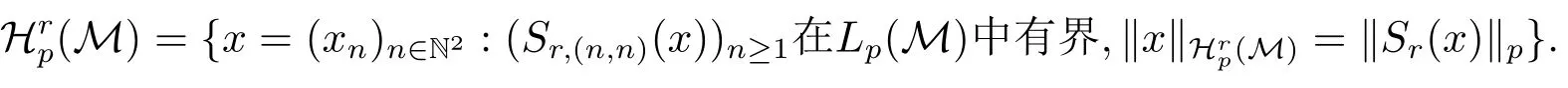
(ii)定义非交换鞅Hardy空间如下.

当1≤p≤2时,定义,赋予范数

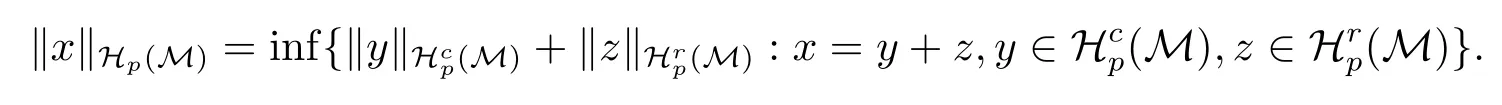
当2≤p＜∞时,定义,赋予范数

注对一个双指标鞅x=(xn,n∈N2)的鞅差序列dx=(dxn)n∈N2,把它重新编号变成一个单指标的序列,则可以把它视为一个单指标序列dx=(xn)(但是要注意的是xn)一般不是单指标的鞅差序列).因此,无论x=(xn)是单指标鞅还是双指标鞅都有

下面定义双指标非交换鞅Hardy空间hp(M).由于这里需要考虑双指标有限鞅,为此先给出双指标有限鞅的知识.设x=(xn,n∈N2)是一个鞅,k∈N,称形如x(k)=(xn1∧k,n2∧k,(n1,n2)∈N2)为停止于k的有限鞅.

设1≤p＜∞,对Lp(M)中的有限鞅x=(xn),定义

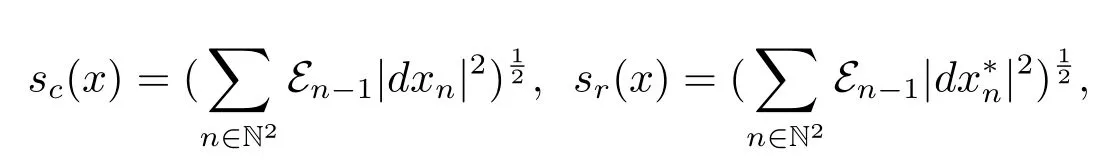
则‖x‖hcp(M)=‖sc(x)‖p,‖x‖hrp(M)=‖sr(x)‖p.还需要考虑lp(Lp(M)),定义

定义2.3(i)设1≤p＜2.定义,赋予范数

(ii)设2≤p＜∞.定义,赋予范数

3 主要结果

在这一部分研究双指标非交换鞅Hardy空间的一些不等式,包括双指标非交换鞅的‖·‖Hp(M)和‖·‖hp(M)之间的关系,双指标非交换序列的Stein不等式以及‖·‖Lp(M)和‖·‖hp(M)之间的等价关系.这些结果是关于单指标鞅相应的结果在双指标鞅相应的推广(见文[3]).

下面的定理3.1是这一节的主要结果.

定理3.1设x=(xn)n∈N2是Lp(M)中的鞅.则

(i) 当 1≤p≤2 时,有‖x‖Hp(M)≤Cp‖x‖hp(M);

(ii)当2≤p＜ ∞时,有‖x‖hp(M)≤p‖x‖Hp(M),其中Cp和p是只依赖于p的常数.

为证明上述定理,需要用到下面的一系列引理.

引理3.2[3,4]设(Mn)n≥1是M的一列单调递增的子von Neumann代数,En表示M到Mn的条件期望算子.则对任意的有限序列,有

这里Cp是只依赖于p的正常数.

下面把引理3.2推广到双指标的情形.

引理3.3设(Mn)n∈N2是M的一列关于N2偏序单调递增的子von Neumann代数,En表示M到Mn的条件期望算子,则对任意的有限双指标序列,有

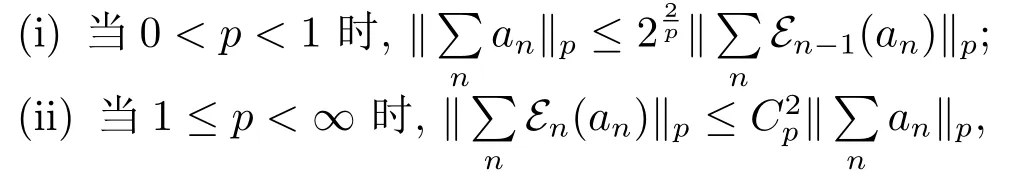
这里Cp与引理3.2中的Cp一致.

证 (i)利用(F4)条件和引理3.2,有

(ii)证明方法与(i)的证明是类似的.证毕.

推论3.4(双指标序列的Stein不等式)设2≤p＜∞,则对Lp(M)中任意的有限双指标序列(an),有

这里Cp与引理3.3中的Cp一致.

证利用引理3.3和不等式E(x)∗E(x)≤E(|x|2),得到

定理证毕.

引理3.5设1≤p＜∞.则对任意的有限双指标序列(xn)⊂Lp(M),有

(i)当2≤p＜∞时,

(ii)当1≤p≤2时,

证(i)将(xn)n∈N2进行重新编号为一个单指标的序列,再利用非交换单指标的结论(见文[7]),就得到所要证明的不等式.

(ii)证明方法与(i)的证明是类似的.引理证毕.

定理3.1的证明(i)先考虑有限鞅的情形.设x=(xn)为hp(M)中停止于k的有限鞅.设x=y+z+w是x的一个分解,其中y,z分别为中的有限鞅,,满足dwk=0,∀k(n,n).由于,由引理3.3(i),有

利用引理3.5(ii),得到

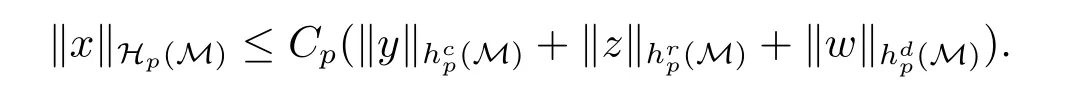
对x的所有分解取下确界,得到‖x‖Hp(M)≤Cp‖x‖hp(M).

一般情形,设x=(xn)n∈N2∈hp(M).对任意的k∈N,令x(k)=(xn1∧k,n2∧k)n∈N2.由上面证明得到‖x(k)‖Hp(M)≤Cp‖x(k)‖hp(M).再令k→∞得到‖x‖Hp(M)≤Cp‖x‖hp(M).

(ii)与(i)的证明类似,也先考虑有限鞅的情形.设x=(xn)为Hp(M)中停止于k的有限鞅.由引理3.3(ii)得到

一般情形,先考虑有限鞅,再取极限即得到所要的结论.定理证毕.

下面转到双指标非交换鞅的Burkholder不等式.要用到下面的双指标非交换鞅的Burkholder-Gundy不等式.

引理3.6[7]设1＜p＜∞.x=(xn,n∈N2)是Lp(M)中的鞅,则x是Lp-有界鞅当且仅当x∈Hp(M).更确切地说,有这里的αp,βp是只与p有关的正常数.

定理3.7设2≤p≤4,x=(xn,n∈N2)是Lp(M)中的鞅,则x是Lp-有界鞅当且仅当x∈hp(M).更确切地说,有

这里的αp,βp为引理3.6中的常数,为定理3.1(ii)中的常数.

证首先证明第一个不等式.事实上,由定理3.1(ii)和引理3.6可知

接下来证明第二个不等式.由引理3.6知‖x‖p≤βp‖x‖Hp(M).下面只需再证明

不妨设‖x‖hp(M)≤1.有

令|dxn|2=En-1|dxn|2+dyn(n∈N2),这里dyn=|dxn|2-En-1|dxn|2.注意到,有

这里y是一个鞅.注意到,利用引理3.5(ii)和引理3.6,得到

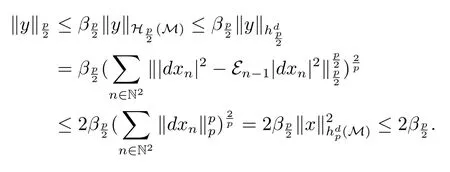
定理证毕.

由定理3.7和定理3.1(ii)得到如下推论.

推论3.8设2≤p≤4,对任意的Lp-有限鞅x=(xn,n∈N2),有

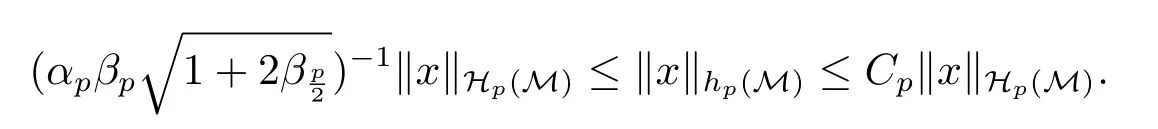
证第二个不等式直接由定理3.1得到.对于第一个不等式,由引理3.6和定理3.7得到.证毕.

[1]Cuculescu I.Martingales on von Neumann algebras[J].J.Multi.Anal.,1971,1：17-27.

[2]Pisier G,Xu Quanhua.Non-commutative martingale inequalities[J].Comm.Math.Phys.,1997,189：667-698.

[3]Junge M,Xu Q.Noncommutative Burkholder/Rosenthal inequalities[J].Ann.Prob.,2003,31：948-995.

[4]Junge M.Doob’s inequalities for non-commutative martingales[J].J.Reine Angew.Math.,2002,549：149-190.

[5]Weisz F.Martingale Hardy spaces and their application in Fourier analysis[M].Berlin：Springer-Verlag.1994.

[6]Pisier G,Xu Quanhua.Non-commutativeLp-spaces[M].Vol.II,Holland：Elsevier,2003.

[7]曹芳.双指标非交换鞅的收敛性和不等式[J].数学杂志,2015,35(6)：1511-1520.

INEQUALITIES OF TWO-PARAMETER NONCOMMUTATIVE MARTINGALES

YIN Di,MA Cong-bian
(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)

In this paper,we discuss the inequalities of two-parameter noncommutative martingales.By using the inequalities of one-parameter noncommutative martingales methods,we obtain the relation between‖ ·‖Hp(M)and‖ ·‖hp(M)of two-parameter noncommutative martingales(2≤p＜∞),which generalize the equivalence relation between‖·‖Lp(M)and‖·‖hp(M)of two-parameter noncommutative martingales(2≤p≤4).

von Neumann algebra;two-parameter martingales;Burkholder inequalities;martingale Hardy spaces

on：46L52;46L53;60G42

O177.5

A

0255-7797(2017)04-0851-08

2015-07-10接收日期：2015-09-14

国家自然科学基金资助(11271293;11471251).

尹磾(1991-),男,湖南益阳,硕士,主要研究方向：Hp鞅论.