α-混合的部分线性EV模型的矩收敛性

金丽宏

(武汉科技大学城市学院公共课部,湖北武汉 430083)

α-混合的部分线性EV模型的矩收敛性

金丽宏

(武汉科技大学城市学院公共课部,湖北武汉 430083)

本文研究误差为α-混合的部分线性EV模型的矩收敛性问题.利用小波估计和修正最小二乘法,给出了参数和非参数部分的小波估计量,获得了小波估计量的矩收敛速度,推广了现有的一些结论.

α-混合;部分线性EV模型;小波估计;修正最小二乘法;矩收敛速度

1 引言

本文研究如下部分线性EV(errors-in-variables)模型

其中Xi∈R,ti∈R,i=1,2,···,n是已知的点列,β是未知参数,g(·)是定义在[0,1]上的未知函数,误差{ei,i=1,2,···,n}是平稳的α-混合随机变量且Eei=0和.{xi}是通过Xi=xi+ςi观测到的,{ςi}是独立同分布的测量误差,且且和{ei}是独立的.

定义1[1]设{ξi,i≥1}是α-混合的,如果α-混合系数

当n→∞时收敛到0,其中表示包含ξl,ξl+1,···,ξm,l≤m的σ-代数.

文献[2]用加权的方法研究了异方差α-混合半参数模型,得到了估计量的Berry-Esseen界;文献[3]研究了部分线性变系数EV模型,得到了估计量的渐近性质;文献[4]用加权的方法研究了误差独立的半参数回归模型的矩相合性;文献[5]用加权的方法研究了NA样本下部分线性回归模型的矩相合性;文献[6]用小波方法研究了鞅差时间序列半参数回归模型的矩收敛速度;文献[7]用小波方法研究了φ-混合和ψ-混合的非参数回归模型的矩收敛速度.然而对α-混合的部分线性EV模型的矩收敛性还没有研究,因此本文研究模型(1.1)的矩收敛性.

本文用小波方法研究模型(1.1),仍采用文献[8]修正后的最小二乘估计,即

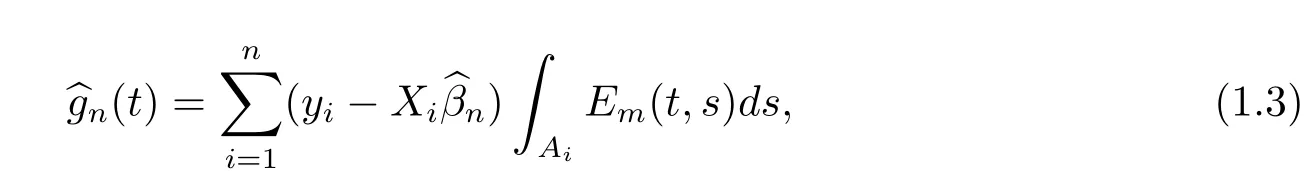
2 引理

下面是本文的基本假设.

(1)xi=f(ti)+ηi,i=1,2,···,n,其中f(·) 是定义于 [0,1]的函数,{ηi}i.i.d 且Eηi=0,Var(ηi)=ση,而且 {ηi} 和 { (ei,ςi)} 是相互独立的.

(2)g(·)和f(·)∈Hα(Sobolev 空间),

(3)g(·),f(·)满足κ阶 Lipschitz 条件,κ＞0.

(4)φ(·)∈Sι(阶为ι的Schwartz空间,ι≥α),φ满足1阶Lipschitz条件且具有紧支撑,当ξ→0时,|(ξ)-1| =o(ξ),其中为φ的Fourier变换.

注1条件(1)是文献[8]的特殊情形,条件(2)-(5)是小波估计中经常用到的(如文献[9-11]等).由此可见本文的假设条件是相当一般的.

引理1[12]若条件(1)-(5)成立,则

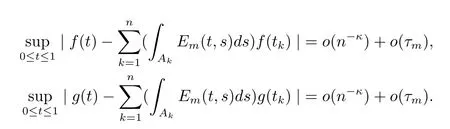
引理2[13]若条件(5)成立,其中k∈N,Ck只与k有关的实数,则有

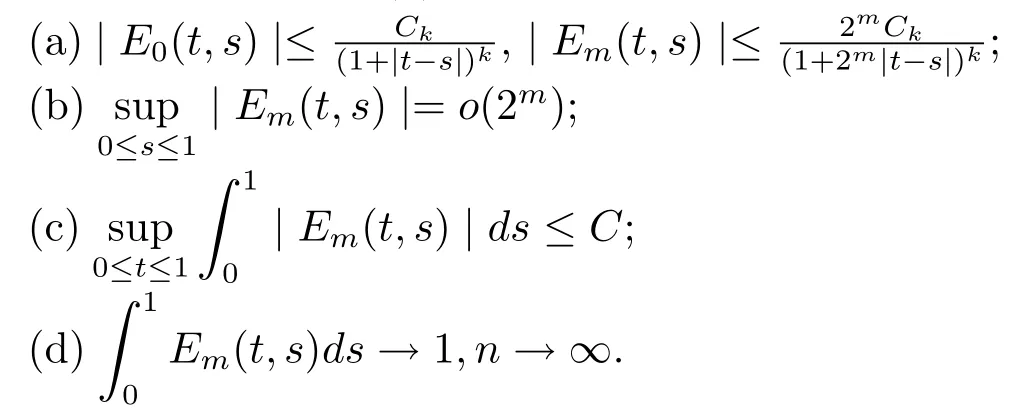
引理3若条件(1)-(5)成立,则

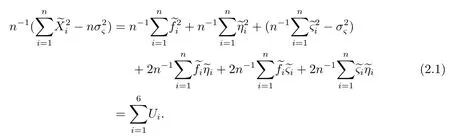
证注意到由引理1可得U1→0.由强大数定理和

(见文献[14]),有

同理,很容易证明U3→0 a.s..使用Cauchy-Schwarz不等式,有

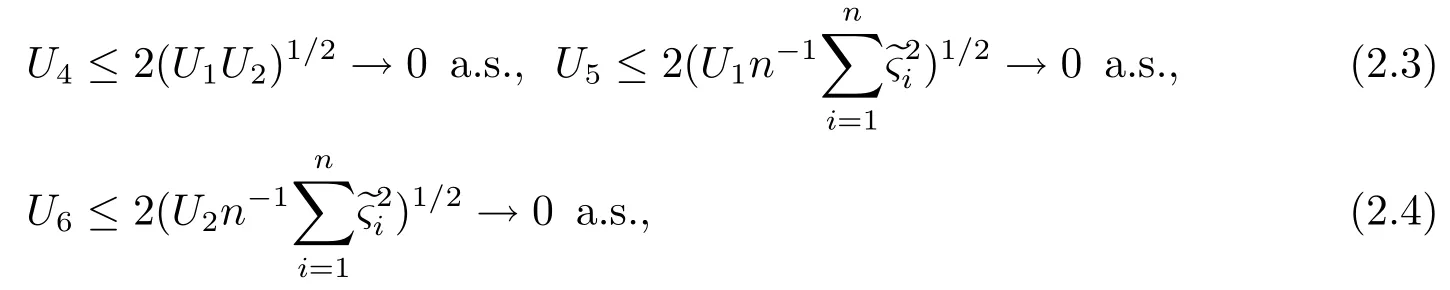
由(2.1)-(2.4)式即得引理3.

引理4[13](1)存在δ＞0,使得Eei=0且E|ei|2+δ＜∞,则

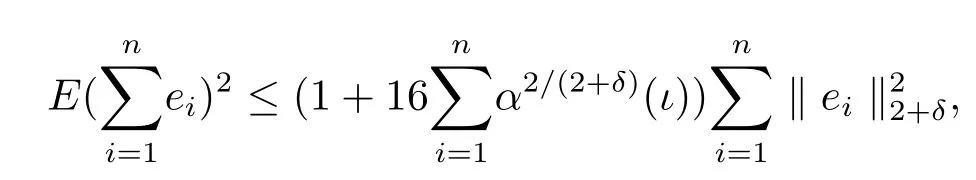
其中 ‖ei‖2+δ=(E|ei|2+δ)1/(2+δ).

(2)存在r＞2,δ＞0,λ＞和α(n)=o(n-λ),使得Eei=0且E|ei|r+δ＜∞,则∀ε＞0,存在正整数c=c(k,r,δ,λ),有

引理5[15]如果{Xk}是数学期望为0的独立r.v.序列,那么对r≥2,

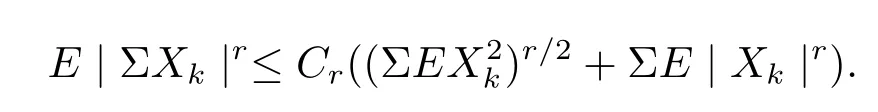
引理6如果{ξi,i≥1}是α-混合的随机变量,{ζi,i≥1}是独立的随机变量,那么{ξiζi,i≥1}也是α-混合的随机变量.

证令表示包含ξι,ξι+1,···,ξm,ι≤m的σ-代数;

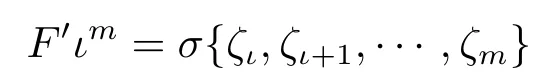
表示包含ζι,ζι+1,···,ζm,ι≤m的σ-代数;

表示包含ιm=σ{ξιζι,ξι+1ζι+1,···,ξmζm},ι≤m的σ-代数.,有

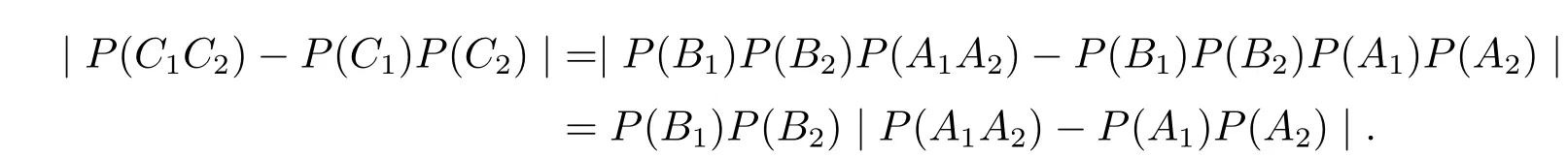
因为{ξi,i≥1}是α-混合的随机变量,所以{ξiζi,i≥1}也是α-混合的随机变量.

3 主要结果及证明

定理1若本文假设(1)-(5)成立,且存在r＞2,δ＞0,λ＞和α(n)=o(n-λ),使得,且满足

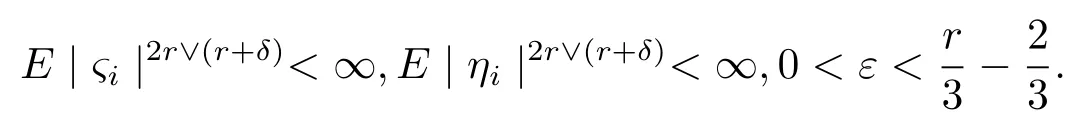
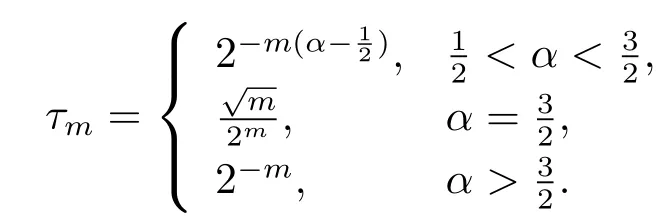
则

由Cr不等式,引理3,引理5和Cauchy-Schwarz不等式有

由Cr不等式,引理1,引理3和引理5,有

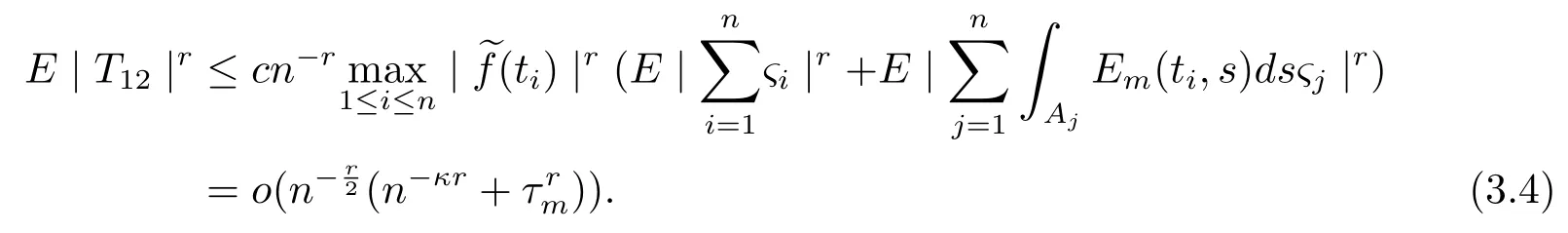
由Cr不等式,引理3和引理5,有

由Cr不等式,引理1,引理3和引理5,有

由Cr不等式,引理3,引理4,引理5和引理6,有

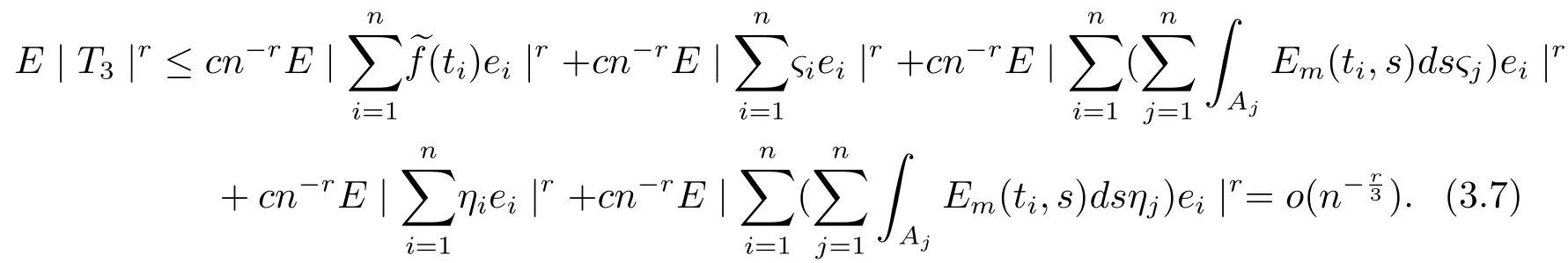
由Cr不等式,引理1,引理3和引理4,有

由Cr不等式,(3.1)-(3.8)式,得

定理1得证.

定理2若本文假设(1)-(5)成立,且存在r＞2,δ＞0,λ＞和α(n)=o(n-λ),使得,且满足

证注意到

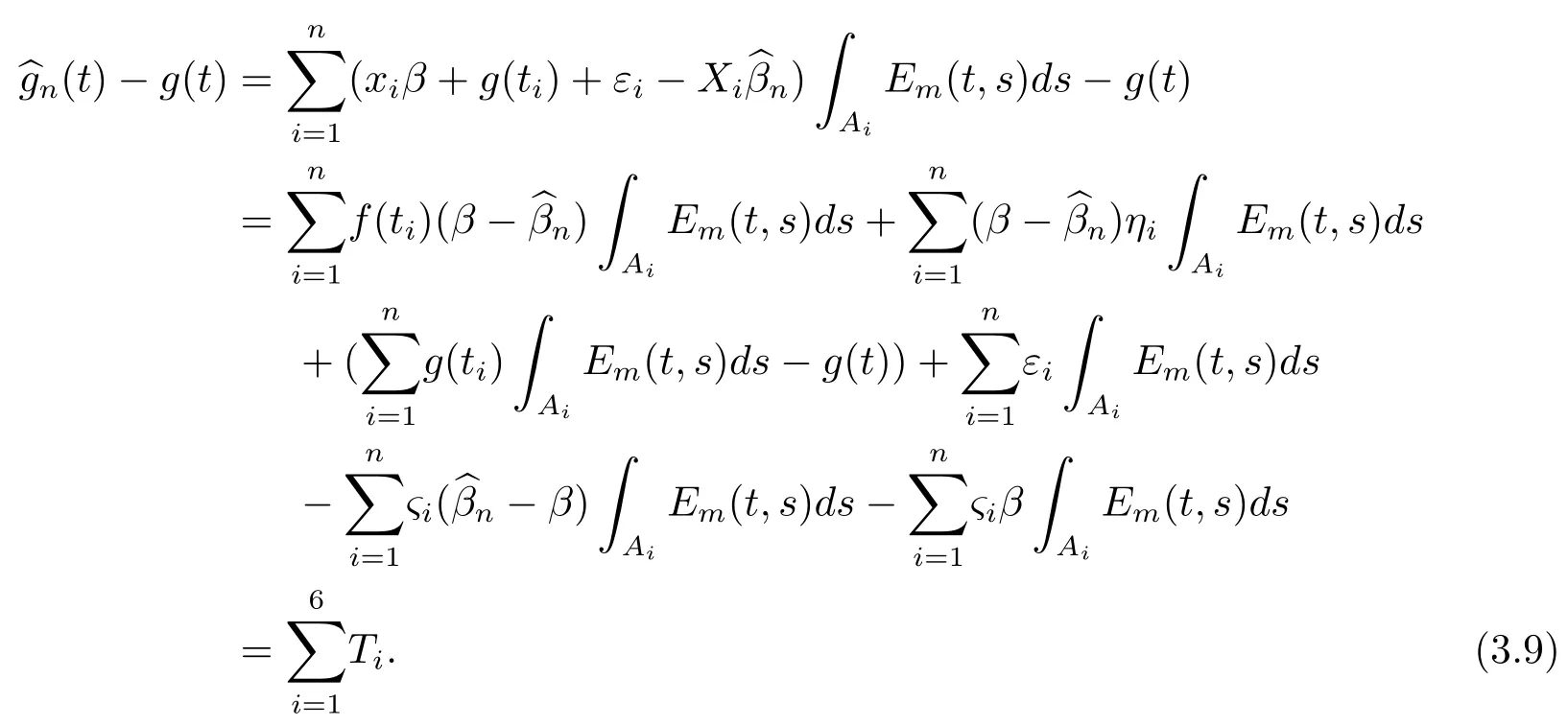
由引理2,有

由Cauchy-Schwarz不等式和引理5,有

由引理1,可得

由引理4,有

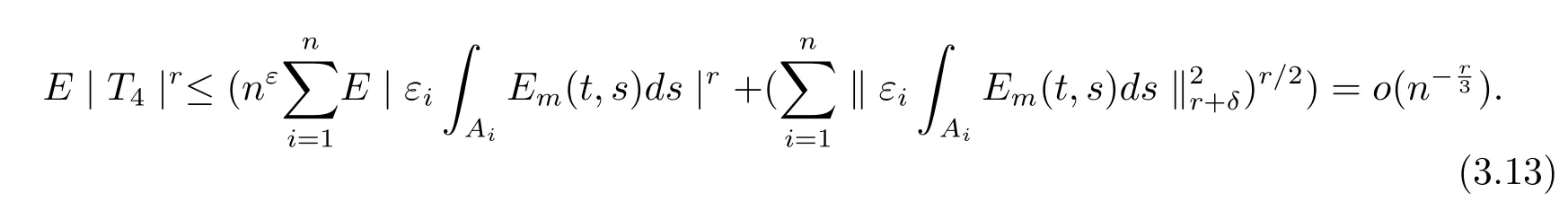
由Cauchy-Schwarz不等式和引理5,有

由引理5,有

由Cr不等式和(3.10)-(3.15)式,有

定理2得证.

注2当ςi=0时,模型(1.1)退化为一般的部分线性回归模型,因此模型(1.1)是一般的部分线性模型的推广.文献[4]要求ei独立而本文只需ei是α-混合,在条件比文献[4]弱的情况下,由定理1和定理2可以直接得到文献[4]相应的结论.进一步,当β=0时模型(1.1)退化为非线性模型,在文献[7]中要求ei是φ-混合,而模型(1.1)是α-混合比文献[7]的条件弱,因此文献[7]的结论是定理2的推论.

[1]Fan J,Yao Q.Nonlinear time series：nonparametric and parametric methods[M].Berlin：Springer-Verlag,2003.

[2]Zhang J J,Liang H Y.Berry-Esseen type bounds in heteroscedastic semiparametric model[J].J.Stat.Plan.Infer.,2011,141：3447-3462.

[3]Zhang W W,Li G R,Xue L G.Po fi le interence on partially linear varing-coefficent errors-in-variables models under restricted condition[J].Comp.Stat.Data Anal.,2011,55：3027-3040.

[4]胡舒合.一类半参数回归模型的估计问题[J].数学物理学报,1999,19(5)：541-549.

[5]Zhou X C,Liu X S,Hu S H.Moment consistency of estimators in partially linear models under NA samples[J].Metrika,2010,72：415-432.

[6]胡宏昌,胡迪鹤.鞅差时间序列半参数回归模型的小波估计[J].数学进展,2010,39(1)：23-30.

[7]薛留根.混合误差下回归函数小波估计的一致收敛速度[J].数学物理学报,2002,22A(4)：528-535.

[8]Liang H,Hardle W,Carrool R J.Estimation in a semiparametric partially linear errors-in-variables model[J].Ann.Stat.,1999,27：1519-1535.

[9]Antoniads A,Gregorie G,Mckeague I W.Wavelet methods for curve estimation[J].J.Amer.Stat.Assoc.,1994,89：1340-1353.

[10]Hu H C,Wu L.Convergence rates of wavelet estimators in a semiparametric regression models under NA samples[J].Chinese Ann.Math.,2012,33(4)：609-624.

[11]Zhou X,You J H.Wavelet estimation in varying-coefficient partially linear regression models[J].Stat.Prob.Lett.,2004,68：91-104.

[12]胡宏昌,胡迪鹤.半参数回归模型小波估计的强相合性[J].数学学报,2006,49(6)：1417-1424.

[13]Qian W M,Cai G X.Strong approximability of wavelet estimate in semiparametric regression models[J].Sci.China(Ser.A),1999,29：233-240.

[14]Hu H C.Convergence rates of wavelet estimators in semiparametric regression models with martingale di ff erence error[J].J.Math.Sci.：Adv.Appl.,2009,3：4-19.

[15]林正炎,白志东.概率不等式[M].北京：科学出版社,2005：104.

[16]方连娣,胡凤霞.核实数据下非线性EV模型中经验似然降维推断[J].数学杂志,2012,32(1)：113-120.

THE MOMENT CONVERGENCE RATES OF PARTLY LINEAR ERRORS-IN-VARIABLES MODEL WITH α-MIXING ERRORS

JIN Li-hong

(Department of Basic,College of City,Wuhan University of Science and Technology,Wuhan 430083,China)

In this paper,we discuss the moment convergence rates of partly linear errorsin-variables model.Using wavelet smoothing and modi fi ed least-squares methods,we investigate a partly linear errors-in-variables model withα-mixing sequence,the wavelet estimators of the parametric parts and nonparametric parts are given.We obtain the moment convergence rates of wavelet estimators,which extend some present conclusions.

α-mixing;partly linear errors-in-variables model;wavelet estimation;modi fi ed least-squares;moment convergence rate

on：62J05

O212.1

A

0255-7797(2017)04-0797-08

2016-12-21接收日期：2016-12-22

国家自然科学基金资助(40974002;41374017;11471105).

金丽宏(1976-),女,汉,湖北仙桃,副教授,主要研究方向：测量数据的处理与应用的研究.