复线性微分方程解的增长性的几个结果

龙见仁

(北京邮电大学计算机学院;理学院,北京 100876)(贵州师范大学数学科学学院,贵州贵阳 550001)

复线性微分方程解的增长性的几个结果

龙见仁

(北京邮电大学计算机学院;理学院,北京 100876)(贵州师范大学数学科学学院,贵州贵阳 550001)

本文研究了复线性微分方程解的增长性问题.利用两类具有某种渐进增长性质的函数作为线性微分方程的系数,讨论了两类二阶线性微分方程解的增长性,获得了方程解为无穷级.这些结果推广了先前的一些结果.

复微分方程;整函数;无穷级;下级;渐进增长

1 引言及主要结果

对复平面C上的亚纯函数f,其级与下级分别定义为

和

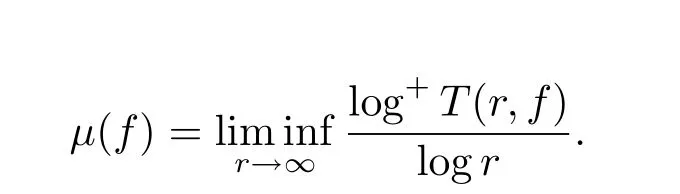
如果f是整函数,则上述定义中的Nevanlinna特征函数T(r,f)可以被logM(r,f)所替代,其中

.从定义容易看到有µ(f)≤ρ(f),并且严格不等式也是可能的,参见文献[1-3].在这篇文章里,我们假设读者熟悉亚纯函数值分布理论的基本记号与主要的结果,例如T(r,f),m(r,f),N(r,f)等,更多的细节参看文献[4-6].

为了陈述下面的结果,先回忆几个记号.集合E⊂[0,∞)的Lebesgue线性测度是,其上、下线性密度分别是

集合F⊂[1,∞)的对数测度是,其上、下对数密度分别是

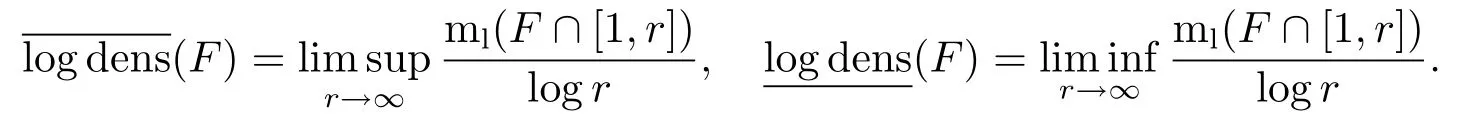
从文献[14,p.121]容易看到,对任意集合F⊂[1,∞),

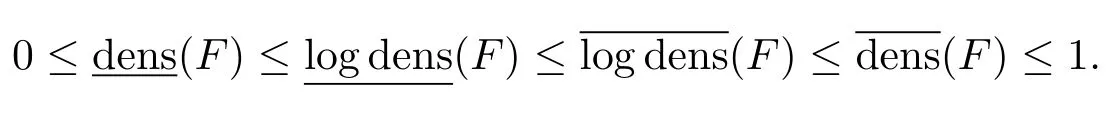
在文献[15]中,Laine-Wu利用系数是具有某种渐进增长性质的整函数去研究复线性微分方程解的增长性,并获得了

定理A设A(z)和B(z)是两个满足ρ(B)＜ρ(A)＜∞的整函数.设A(z)满足

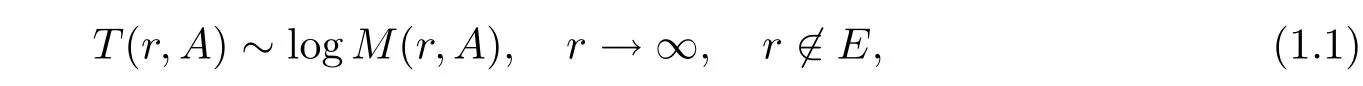
其中ml(E)＜∞,则线性微分方程

的所有非平凡解都是无穷级.

(1.1)式意味着下面极限

在除去一个对数测度有限的r值例外集合上成立.

Kwon和Kim在文献[16]推广了定理A,通过系数A(z)允许除去一个更大的r值例外集使得条件(1.1)成立.

定理B设A(z)和B(z)是两个满足ρ(B)＜ρ(A)＜∞的整函数.设A(z)在除去r值例外集E上满足条件(1.1),其中.则微分方程(1.2)的所有非平凡解都是无穷级.

这里考虑系数的下级对微分方程(1.2)解的快速增长的影响,将定理A、B中系数A(z)和B(z)的级用其下级代替,获得了下面的结果.我们的证明不同于定理A、B,使用了一个来自于Miles-Rossi的结果(见文献[17,定理1]),关于对数导数的反面估计,这个估计在定理A、B的证明中没有使用.

定理1设A(z)和B(z)是两个满足µ(B)＜µ(A)＜∞的整函数.设A(z)在除去r值例外集E上满足条件(1.1),其中则微分方程(1.2)的所有非平凡解都是无穷级.

本文的第二个结果,利用一种新的研究思路去研究线性微分方程解的增长性,即方程(1.2)的系数A(z)是另一个二阶线性微分方程

的非平凡解,其中P(z)=anzn+···+a1z+a0,an/0.众所周知,方程(1.3)的任何非平凡解的增长级为.关于方程(1.3)解的更多的性质,参看文献[7-8,18].Hille[19]利用他的方法刻画了方程(1.3)解的渐进增长.本文的第二结果就是利用方程(1.3)解的渐进性质去研究方程(1.2)解的增长性,获得了

定理2设A(z)是方程(1.3)的一个非平凡解,B(z)是一个ρ(B)/ρ(A)的超越整函数,且

本文的第三个结果涉及到另一类二阶线性微分方程

其中Q(z)是整函数.为此先回顾方程(1.5)解的一些性质.对于Q(z)是多项式的情形,在以往的文献中,可以发现很多关于方程(1.5)解的结论,例如文献[20-23].对于Q(z)是超越整函数,有两个结果值得注意,一个是Gundersen[24]证明了如果Q(z)是超越整函数并且ρ(Q)/1,则方程(1.5)的所有非平凡解都是无穷级.另一个是Chen[25]证明了如果Q(z)=h(z)ebz,其中h(z)是一个非零多项式,b/-1,则方程(1.5)的所有非平凡解都是无穷级.从Chen的结果可以看出当系数Q(z)的增长级等于1时,方程(1.5)有无穷级解.在文献[26]中,Li-Wang讨论了方程(1.5)解的增长性.他们证明了如果Q(z)=h(z)ebz,h(z)是一个级小于的超越整函数,b是一个实常数.则方程(1.5)的所有非平凡解都是无穷级.针对整函数Q(z)级为1的情形,Wang-Laine[27]考虑了线性微分方程

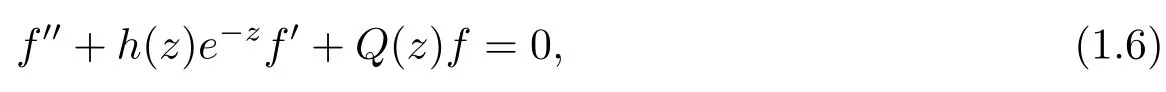
其中h(z)是一个满足ρ(h)＜ρ(Q)=1的整函数.他们假定系数Q(z)具有某一个渐进增长条件时,研究了方程(1.6)解的增长性.

定理C设Q(z)和h(z)是两个满足ρ(h)＜ρ(Q)=1的整函数.设Q(z)满足

相比定理C,这里利用另一类具有某种渐进性质的整函数去研究微分方程(1.6)解的增长性.即对于常数α∈(0,1),如果Q(z)在一个足够大的r值集合上满足

定理3设Q(z)和h(z)是两个满足ρ(h)＜ρ(Q)=1的整函数.设Q(z)在除去一个上对数密度为0的r值集合上对α∈(,1)满足条件(1.7).则微分方程(1.6)的所有非平凡解都是无穷级.

提出条件(1.7)是很自然的,有很多的函数在除去一个适当的r值例外集上满足条件(1.7).一个简单的例子就是Q(z)=ez,条件(1.7)对成立,没有例外集.下面稍微复杂一点的例子可以在文献[28,p.158]中找到.

例1设Q(z)=(1-3eiz)ez2-ze-iz2,则条件(1.7)对成立,没有例外集.

相比例1,更一般的例子就是形如Q(z)=P1(z)eQ1(z)+···+Pn(z)eQn(z)的指数多项式,其中Pj(z),Qj(z)(j=1,···,n)是多项式,参见文献[28].根据定义,容易证明Q(z)是完全正规增长的函数(见文献[29,p.6]).于是有下面的例子.

例2如果Q(z)是上面形式的指数多项式,则根据文献[29,定理1.2.1],有

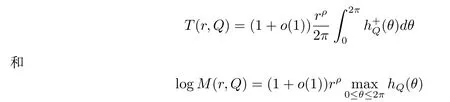
对所有的[0,1]∪E成立,其中(因此所以条件(1.7)在除去一个上对数密度为0的r值例外集上对

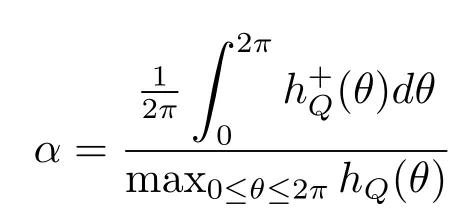
成立.

2 引理

为了证明上述定理,需要如下的几个引理.

引理2.1[30]假设f是一个有穷级超越亚纯函数,k,j是两个满足k＞j≥0的整数.则对任意给定的常数ε＞0,下列三个结论成立.

(1)存在一个集合E1⊂[0,2π),m(E1)=0,使得如果ψ0∈([0,2π)-E1),则存在常数R0=R0(ψ0)＞1,使得对所有满足argz=ψ0,|z|≥R0的z,有

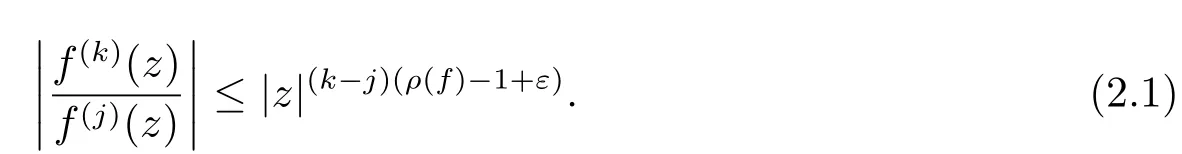
(2)存在一个集合E2⊂(1,∞),ml(E2)＜∞,使得对所有满足|(E2∪[0,1])的z,不等式(2.1)成立.

(3)存在一个集合E3⊂[0,∞),m(E3)＜∞,使得对所有满足|3的z,有

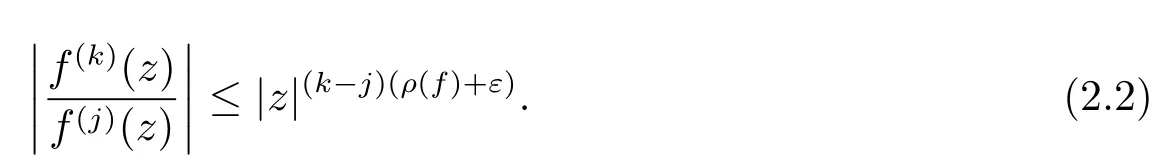
下面的结果是文献[17,定理1]的一个简单形式,但足够本文使用.

引理2.2假设f是一个级为ρ(＜∞)的非常数整函数.对β∈(0,1)及r＞0,令

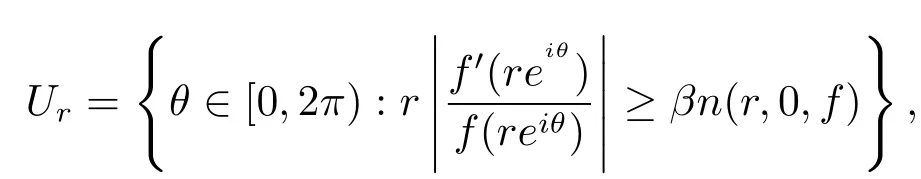
则对M(＞3)存在一个集合EM⊂[1,∞),,使得对所有的r∈EM,

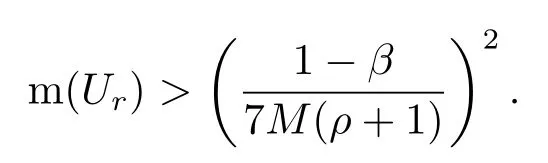
为了介绍Hille关于方程(1.3)解的渐进增长性质,需要一些记号.假设α,β是两个常数满足β-α＜2π及α＜β,对任意r＞0,定义

假设f是一个级为ρ∈(0,∞)的整函数,为了叙述方便,令.如果对任意θ∈(α,β),有

则称f在S内以指数增长趋于无穷;如果对任意θ∈(α,β),有

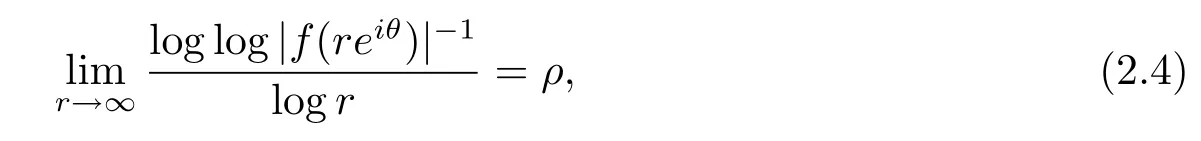
则称f在S内以指数增长趋于零.

下面的结果源自文献[19,第7.4节],也可以在文献[31]找到它的陈述.

引理2.3假设w是方程(1.3)的一个非平凡解,其中P(z)=anzn+···+a1z+a0,an0. 令,Sj=S(θj,θj+1),j=0,1,2,···,n+1,其中θn+2=θ0+2π. 则w具有下面的性质.

(1)在每一个角域Sj,w或者以指数增长趋于无穷,或者以指数增长趋于零.

(2)对某个j,如果w在Sj以指数增长趋于零,则w在Sj+1和Sj-1必须以指数增长趋于无穷.但是w在几个相邻角域以指数增长趋于无穷是可能的.

(3)如果w在Sj以指数增长趋于零,则w在至多有有穷多个零点.

(4)如果w在Sj和Sj-1以指数增长趋于无穷,则对任意给定的ε＞0,w在内有无穷多个零点.进一步有,当r→∞,

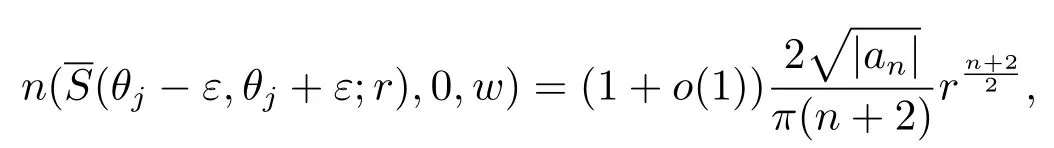
引理2.4[27]设f是级为ρ(＜∞)的整函数,对每一个r＞0,令M(r,f)=f(reiθr).对

给定的ζ＞0和0＜C(ρ,ζ)＜1,则存在一个常数和一个集合,使得对所有充分大的r∈Eζ及所有满足|θ-θr|≤l0的θ,

在文献[32,定理3],Gundersen证明了下面的结果.

引理2.5设A(z)和B(z)(0)是两个整函数,对实数α,β,θ1,θ2,其中α＞0,β＞0及θ1＜ θ2,当z→ ∞,(θ1,θ2)={z：θ1≤argz≤θ2},有

和

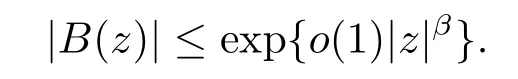
对任意给定的ε＞0,令如果f是方程(1.2)的级为ρ(f)(＜∞)的非平凡解.则下列结论成立.

(1)存在一个常数b(/=0)使得当z→ ∞,(θ1+ε,θ2-ε),f(z)→b. 进一步有当z→ ∞,(θ1+ε,θ2-ε),

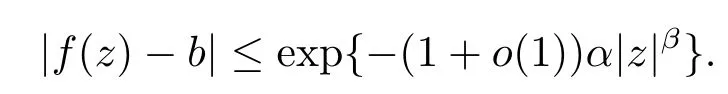
(2)对每一个k＞1,当z→ ∞,(θ1+ε,θ2-ε),有

下面的引理描述了函数eP(z)的性质,其中P(z)是一个线性多项式.关于这类函数更一般的性质参看文献[33,p.254].

引理2.6设P(z)=(α+iβ)z,其中α,β是两个实数满足 |α|+|0.假设A(z)(0)是一个级小于1的亚纯函数.令g(z)=A(z)eP(z),δ(P,θ)=αcosθ-βsinθ,其中z=reiθ,则对任意给定的ε＞0,存在一个集合E⊂(1,∞),m(E)＜∞,使得对任意的θ∈[0,2π)-H,有一个实数R＞0,使得对所有满足|z|=r＞R及的z,有

(1) 如果δ(P,θ)＞0,则

(2) 如果δ(P,θ)＜0,则

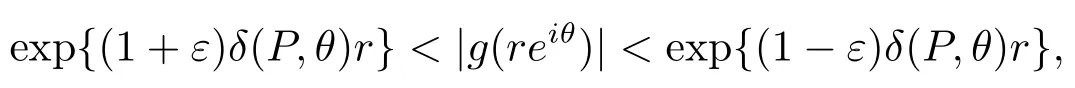
其中H={θ∈[0,2π)：δ(P,θ)=0}.

3 定理的证明

定理1的证明假设方程(1.2)有一个级为ϱ(f)(＜∞)的非平凡解f,将看到一个矛盾.对于给定的常数,定义

因为A(z)在|z|=上满足条件(1.1),其中.所以不难知道存在一个集合F1⊂[1,∞),,使得

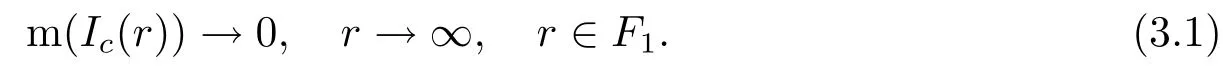
其中

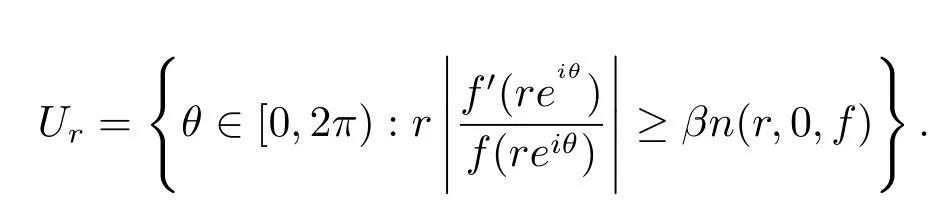
结合(3.1)和(3.2)式,存在θ0∈Ur-Ic(r),对充分大的r∈F1∩F2,有

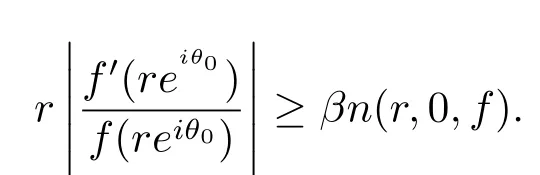
使用类似于文献[32,p.426]的推导,不难得到方程(1.2)的任何非平凡解至少存在一个零点.因此对θ0∈Ur-Ic(r),及充分大的r∈F1∩F2,有

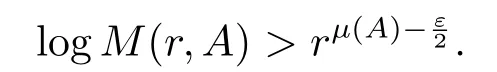
于是对θ0∈Ur-Ic(r),r∈F1∩{r：r≥r0},

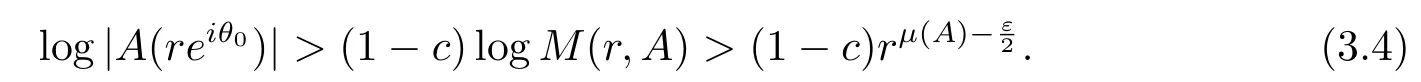
对于B(z),存在一个无穷序列(rn),当n→∞,rn→∞,使得

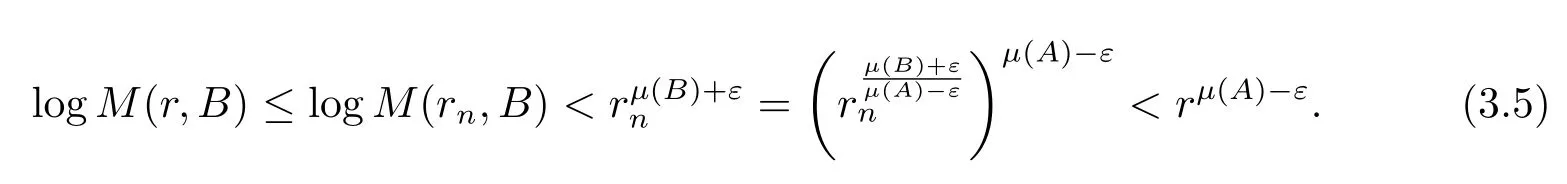
应用引理2.1,存在一个集合F4∈(1,∞),ml(F4)＜∞,使得对所有满足|z|=(F4∪[0,1])的z,有

令F=F1∩{r：r≥r0}∩F2∩F3.通过计算知

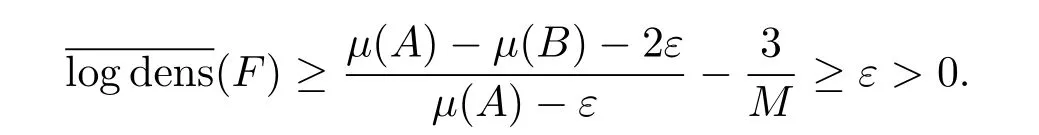
所以在集合F-(F4∪[0,1])中存在一个无穷数列(tj),当j→∞,tj→∞,使得(3.3)-(3.6)式成立.于是结合方程(1.2),有

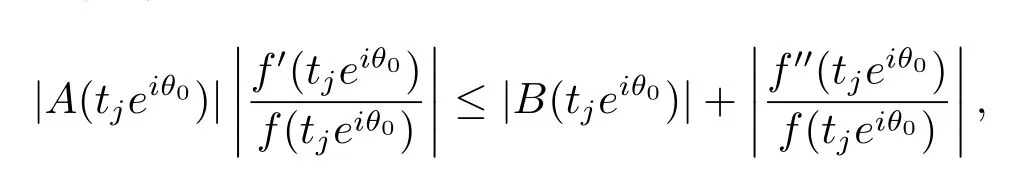
从而有

显然对充分大的j,这是一个矛盾,所以定理得证.

定理2的证明如果ρ(A)＜ρ(B),则定理的结论已被Gundersen证明文献[32,定理2].因此假定ρ(A)＞ρ(B).假设方程(1.2)有一个级为ρ(f)(＜∞)的非平凡解f,将得到一个矛盾.由定理条件知A(z)是方程(1.3)的一个非平凡解,其中P(z)=anzn+···+a1z+a0,an0. 令及Sj={z：θj＜argz＜θj+1}(j=0,1,2,···,n+1),其中θn+2=θ0+2π.依据引理2.3分两种情形证明.

(1)假设A(z)在所有的Sj(j=0,1,···,n+1)里都以指数增长趋于无穷,即对任意的θ∈(θj,θj+1),有

和

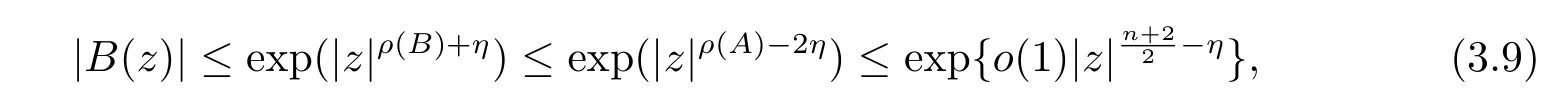
其中α是一个依赖于ε的正常数.结合(3.8),(3.9)式和引理2.5,存在一个相应的常数bj/0,使得当z→∞,z∈Sj(ε)(j=0,1,···,n+1),

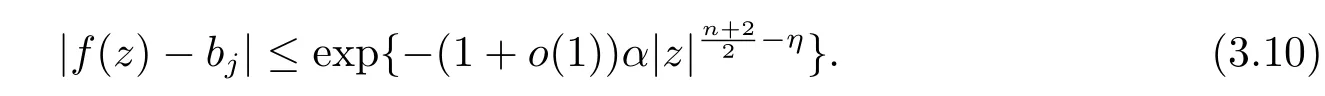
(2)假设在n+2个角域Sj(0≤j0≤n+1)里至少存在一个角域使得A(z)以指数增长趋于零,不妨假设是Sj0={z：θj0＜argz＜θj0+1}(0≤j0≤n+1).这就意味着对任意的θ∈(θj0,θj0+1),有

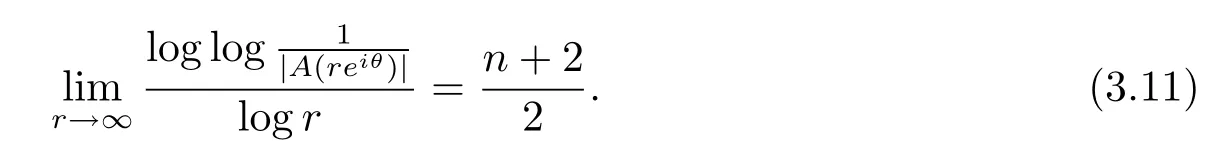
因为在集合E上B(z)满足条件(1.4),令.所以不难看到当r→∞且r∈E,有m(Id(r))→0.利用引理2.1和引理2.4,可以挑选一个无穷点列zn=rneiθ0,当n→∞,zn→∞,且θ0∈(θj0,θj0+1)-Id(r),使得zn满足(2.1),(3.11)式和

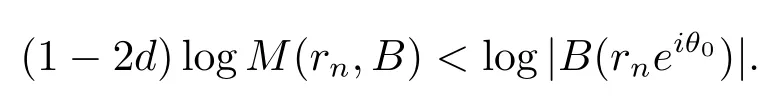
结合上式与(1.2),(2.1),(3.11)式,有

定理3的证明假设方程(1.6)有一个级为ρ(f)(＜∞)的非平凡解f,将看到一个矛盾.对给定的0＜l＜1,定义

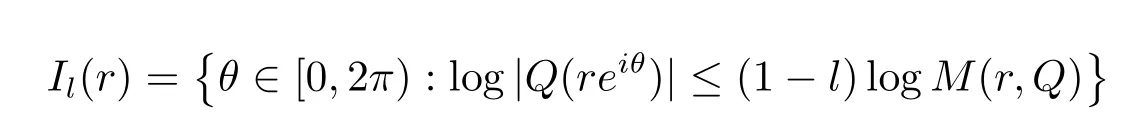
因为在上Q(z)对所有的满足条件(1.7),其中.所以不难看到对任意给定的ε＞0,当r→∞且r/∈E,有.因此对l∈(0,1)充分接近1,则存在一个集合F1⊂[1,∞),使得m(Il(r))＜π,r∈F1.结合引理2.1,存在一个无穷点列zn=rneiθ0,当n→∞,zn→∞且θ0(r),使得(2.1)式和

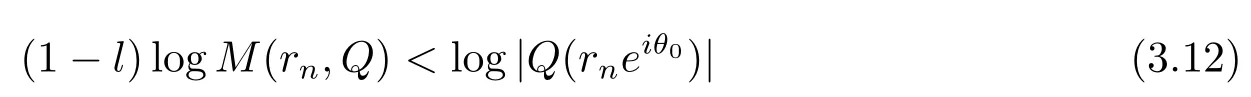
成立,同时δ(-z,θ0)＜0,利用引理2.6,

结合(1.6),(2.1),(3.12)和(3.13)式,对充分大的n,有

因此对充分大的n,有

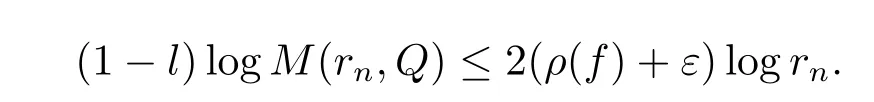
这与Q(z)是超越整函数矛盾,所以方程(1.6)的所有非平凡解都是无穷级.

[1]Edrei A.Locally tauberian theorems for meromorphic functions of lower order less than one[J].Trans.Amer.Math.Soc.,1969,140：309-332.

[2]Edrei A.Solution of the de fi ciency problem for functions of small lower order[J].Proc.London Math.Soc.,1973,26(3)：435-445.

[3]Kobayashi T.On the lower order of an entire function[J].Kodai Math.Sem.Rep.,1976,27：484-495.

[4]Hayman W K.Meromorphic functions[M].Oxford：Clarendon Press,1964.

[5]Yang L.Value distribution theory[M].Berlin：Springer-Verlag,1993.

[6]Zhang G H.Theory of entire and meromorphic functions-de fi cient values,asymptotic values and singular directions[M].Berlin：Springer-Verlag,1993.

[7]Laine I.Nevanlinna theory and complex di ff erential equations[M].New York：Walter de Gruyter Berlin,1993.

[8]Laine I.Complex di ff erential equations[M].Handbook of Di ff erential Equations,Ordinary Di ff erential Equations,Vol.4,Amsterdam：Elsevier,2008.

[9]Long J R,Qiu K E.On the growth of solutions of a class of second order complex linear di ff erential equations(in Chinese)[J].Math.Pract.The.,2015,45(2)：243-247.

[10]Wu P C,Zhu J.On the growth of solutions of the complex di ff erential equationf′′+Af′+Bf=0[J].Sci.China Ser.A,2011,54(5)：939-947.

[11]Wu X B,Long J R,Heittokangas J,Qiu K E.On second order complex linear di ff erential equations with special functions or extremal functions as coefficients[J].Elec.J.Di ff er.Equ.,2015,2015(143)：1-15.

[12]Long J R.Growth of solutions of higher order complex linear di ff erential equaitons in an angular domain(in Chinese)[J].J.Math.,2015,35(6)：1533-1540.

[13]Long J R,Wu P C,Zhang Z.On the growth of solutions of second order linear di ff erential equations with extremal coefficiencts[J].Acta Math.Sin.(Eng.Ser.),2013,29(2)：365-372.

[14]Tsuji M.Potential theory in modern function theory(2nd ed.)[M].Tokyo：Maruzen,1959.

[15]Laine I,Wu P C.Growth of solutions of second order linear di ff erential equations[J].Proc.Amer.Math.Soc.,2000,128(9)：2693-2703.

[16]Kwon K,Kim J.Maximum modulus,characteristic,de fi ciency and growth of solutions of second order linear di ff erential equation[J].Kodai Math.J.,2001,24(3)：344-351.

[17]Miles J,Rossi J.Linear combinations of logarithmic derivatives of entire functions with applications to di ff erential equations[J].Paci fi c J.Math.,1996,174(1)：195-214.

[18]Bank S,Laine I.On the oscillation theory off′′+Af=0 whereAis entire[J].Trans.Amer.Math.Soc.,1982,273(1)：351-363.

[19]Hille E.Lectures On ordinary di ff erential equations[M].California,London,Don Mills,Ontario：Addison-Wesley Publiching Company,1969.

[20]Amemiya I,Ozawa M.Non-existence of fi nite order solutions ofw′′+e-zw′+Q(z)w=0[J].Hokkaido Math.J.,1981,10：1-17.

[22]Langley J.On complex oscillation and a problem of Ozawa[J].Kodai Math.J.,1986,9：430-439.

[23]Ozawa M.On a solution ofw′′+e-zw′+(az+b)w=0[J].Kodai Math.J.,1980,3：295-309.

[24]Gundersen G G.On the question of whetherf′′+e-zf′+B(z)f=0 can admit a solution0 of fi nite order[J].Proc.Roy.Soc.Edinburgh Sect.A,1986,102：9-17.

[25]Chen Z X.The growth of solutions off′′+e-zf′+Q(z)f=0 where the order(Q)=1[J].Sci.China Ser.A.,2002,45(3)：290-300.

[26]Li Y Z,Wang J.Oscillation of solutions of linear di ff erential equations[J].Acta Math.Sin.(Eng.Ser.),2008,24(1)：167-176.

[27]Wang J,Laine I.Growth of solutions of second order linear di ff erential equations[J].J.Math.Anal.Appl.,2008,342：39-51.

[28]Steinmetz N.Zur wertverteilung von exponentialpolynomen[J].Manuscripta Math.,1978,26(1-2)：155-167.

[29]Ronkin L I.Functions of completely regular growth[M].Translated from the Russian by Ronkin A and Yedvabnik I.Math.Appl.(Soviet Ser.),81.Dordrecht：Kluwer Academic Publishers Group,1992.

[30]Gundersen G G.Estimates for the logarithmic derivative of a meromorphic function,plus similar estimates[J].J.London Math.Soc.(2),1988,37(1)：88-104.

[31]Shin K C.New polynomialsPfor whichf′′+P(z)f=0 has a solution with almost all real zeros[J].Ann.Acad.Sci.Fenn.Math.,2002,27：491-498.

[32]Gundersen G G.Finite order solutions of second order linear di ff erential equations[J].Trans.Amer.Math.Soc.,1988,305(1)：415-429.

[33]Markushevich A.Theory of functions of a complex variable[M].Vol.II,New York：Chelsea Publ.,1985.

SOME RESULTS ON THE GROWTH OF SOLUTIONS OF COMPLEX LINEAR DIFFERENTIAL EQUATIONS

LONG Jian-ren
(School of Computer Science;School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China)(School of Mathematical Science,Guizhou Normal University,Guiyang 550001,China)

In this paper,we study the growth problem of solutions of two classes of second order linear di ff erential equations.By assuming their coefficients which have the properties of asymptotic growth,we obtain that all nontrivial solutions are of in fi nite order,which improves and extends previous results.

complex di ff erential equations;entire functions;in fi nite order;lower order;asymptotic growth

on：34M10;30D35

O174.5

A

0255-7797(2017)04-0781-11

2016-03-03接收日期：2016-04-19

国家自然科学基金资助(11501142);贵州省科学技术基金资助(黔科合J字[2015]2112号);贵州师范大学2016年博士科研启动项目资助.

龙见仁(1981-),男,苗族,贵州锦屏,副教授,主要研究方向：复分析.