码头-缆绳-动力定位船舶耦合系统的时频特性分析
2017-07-18朱克强包雄关张大朋
刘 建,朱克强,包雄关,张大朋
(宁波大学 海运学院,浙江 宁波 315211)
码头-缆绳-动力定位船舶耦合系统的时频特性分析
刘 建,朱克强*,包雄关,张大朋
(宁波大学 海运学院,浙江 宁波 315211)
为研究系泊状态下动力定位船舶与码头及缆绳间的耦合作用,采取凝集质量法计算系泊缆索有效张力,设置弹簧阻尼单元用以计算码头碰垫间的非线性反力,应用比例-积分-微分控制系统(PID)进行推力控制。在系泊状态下,以动力定位船舶和无动力定位船舶为研究对象,分析了耦合系统中侧推器对消除因一阶波浪载荷而引起的船舶运动影响的作用;针对动力定位船舶,讨论了码头-缆绳及目标位置两个因素对动力定位船舶的定位能力及侧推器性能的影响。结果表明,在选取合理目标位置的情况下,耦合系统中的侧推器性能及动力定位船舶的定位能力均得到了有效提高。
动力定位;一阶波浪载荷;耦合系统;时频特性
0 引言
随着海洋开发不断向深海拓展,传统的船舶固定方式已经不能满足当前工程作业的需要,动力定位船舶由于机动性能好,定位精度高,且不受水深限制等优点已经得到了广泛的研究和应用[1-2]。
TANNNURI et al[3]针对动力定位系统作用下穿梭油轮的卸载工况响应进行了研究。WICHERS et al[4]对动力辅助定位在深水FPSO上的应用进行了相关探索,完善了动力辅助锚泊定位系统的设计思路。ZHU et al[5]对采用锚泊辅助动力定位的半潜船进行了相关分析,探究了单缆断裂对整体系统的影响。张大朋 等[6]利用水动力分析软件OrcaFlex对不同浪向下船舶的动力定位情况进行了有关动力学分析。宋林峰 等[7]对S型铺管船的铺管工况进行了耦合运动分析,阐明了在低频波浪条件下,耦合作用力是不容忽视的。孙丽萍 等[8]在前人的基础上,对S型铺管船做了全耦合动力定位时域分析,研究中对数值模拟的PID控制方法进行了改进,并采用序列二次规划法分配推进器的推力,论述了垂荡和首摇所引发的耦合作用力会对动力定位系统的性能产生重大影响。
系泊状态下的船舶与码头、缆索、水体等一起组成了复杂的弹性结构体系,其中缆索的张力与系泊船舶的运动紧密相联,在风、浪、流的联合作用下,由于系泊缆索施加的强制约束,形成了环境-船舶-缆索-码头的复杂耦合响应[9]。在此期间,船舶会与码头发生周期性的碰撞,如果撞击载荷过大,将会导致船体及码头的剧烈振动,严重影响船舶结构的安全。
动力定位船舶依靠主推进器、舵和侧推器的作用,使自身的水平三自由度保持在预定的目标位置[10]。一般情况下,动力定位船舶会受到风、浪、流等干扰力的联合作用,其中缓慢变化的水流作用力、风力以及二阶波浪力使船舶产生低频运动,一阶波浪力使船产生高频运动,由于后者以较高的频率周期性地变化[11],动力定位系统将无法消除这部分运动,从而使得外载荷中的波浪力对动力定位船舶的影响最为复杂。
本文针对系泊状态下的动力定位船舶(DP Vessel),结合系统水动力性能的计算结果,阐述了在波浪力、水流作用力、风力、系泊缆绳回复力和动力定位侧推力等外载荷的联合作用下,动力定位船舶-缆绳-码头耦合系统在各方面的时频特性。
1 基本理论
1.1 环境载荷
1.1.1 波浪理论
工程上经常以Skjelbreia和Hendrickson提出的Stokes 5th 波理论为参照标准,将ak以幂级数的形式进行展开(其中a为无量纲振幅,k=2π/L表示波数)的方法由于在陡波条件下无法收敛,故本文采用FENTON[12]给出的基于对kH/2进行幂级数展开的Stokes 5th波理论,经数学证明其精确性要优于前一种方法。
1.1.2 风、流作用力和力矩
风力和流力的计算方式是由特定的模型试验得到的无量纲系数结合石油公司国际海事论坛(OCIMF)给出的公式确定的。
风作用于船上的力和力矩可用式(1)~(3)计算:

(1)

(2)

(3)
式中:Cxw为无量纲纵向风力系数;Cyw为无量纲横向风力系数;Cxyw为无量纲风的摇摆力矩系数;ρw为20 ℃时空气的密度,取1.223 kg/m3;Vw为10 m高处的平均风速,kn;AT为船体水面上横向受风面积,m2;AL为船体水面上纵向受风面积,m2;LBP为船舶两柱间长,m;Fxw为风作用于船体上的纵向力,kN;Fyw为风作用在船体上的横向力,kN;Mxyw为风作用于船体上的横摇力矩,kN·m。
流作用于船上的力和力矩可用式(4)~(6)计算。
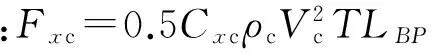
(4)

(5)
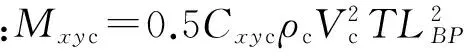
(6)
式中:Cxc为无量纲纵向流力系数;Cyc为无量纲横向流力系数;Cxyc为无量纲流的摇摆力矩系数;ρc为20 ℃时流的密度,取1 025 kg /m3;Vc为平均流速,kn;T为船舶吃水,m;Fxc为流作用于船体上的纵向力,kN;Fyc为流作用在船体上的横向力,kN;Mxyc为流作用于船体上的横摇力矩,kN·m。
公式(1)~(6)中出现的x,y是按照船舶的连体坐标系O-xyz来确定的,其中O为该坐标系的原点,x轴沿船长方向向前,y轴沿船宽方向指向右舷,z轴垂直于xy平面且方向向下。
1.2 动力定位控制方程
作为一种面向对象的动态脚本语言,Python在访问OrcaFlexAPI(application programming interface,应用程序接口)时不需要任何编译器或者链接步骤,由于Python在处理数据类型时的灵活性,设计Python接口作为封装器来访问OrcaFlexDll的内部函数,可以更好地提高程序性能。同时OrcaFlex中的对象数据名称可以完整地复制到Python接口的对象中,以上这些优点使得Python在结合OrcaFlexAPI编写PID动力定位控制系统程序时成为首选语言。
控制系统通过外部函数将动力定位船舶的横荡、纵荡及船舶艏摇与目标值进行比较,经过控制方程的计算,得到DP Vessel所需的回复反力及反力矩,根据推力分配相关原则进行推力分配。推力指令如下:
Fx,y=f(ex,y)
(7)
Mz=f(eθ)
(8)
f(ex,y,θ)=Kpe+KI∫edt+KDde/dt+Fw(aw,vw)
(9)
式中:Fx,y包含有Fx和Fy,分别表示船舶纵荡和横荡方向的回复反力;Mz为船舶艏摇的回复反力矩;ex,ey,eθ分别表示横荡、纵荡、船舶艏摇角和目标值之间的差值;Kp为比例增益;KI为积分增益;KD为微分增益;aw为风向角;vw为风速;Fw为风在该自由度上的反力或反力矩。
1.3 船舶与码头接触碰撞力的计算
由于船体模型在OrcaFlex中被作为刚体处理,因此需要在船体周围覆盖一层弹塑性固体以计算船舶与码头间的碰撞力,进而建立船舶与码头的弹塑性变形动力分析模型,根据弹塑性固体的变形量计算出相应的碰撞力:
Fc=KAcd
(10)
式中:K为弹塑性固体的法向刚度,算例中取为20 000 kN/m3;Ac为碰撞时接触面积,m2,;d为发生碰撞时弹塑性固体垂直方向的变形量,m。
2 动力定位船舶-码头-缆绳计算模型
动力定位船舶的船型参数如表1所示。

表1 动力定位船舶参数
动力定位船舶-码头-缆绳计算模型如图1所示。其中G-xyz为全局坐标系,G为全局坐标系原点,Gx、Gy、Gz分别表示x轴、y轴及z轴,风、浪、流等环境外载荷的方向是相对于G坐标系而言的,并且下文中出现的x,y方向均为该坐标系所描述。

图1 模型示意图Fig.1 Schematic diagram of model
图1中,Link单元作为弹簧阻尼器与6D浮标相连,用来模拟码头碰垫。船舶与码头之间发生碰撞时,碰垫能起到一定的缓冲作用。为使模型更加接近现实,在计算张力时Link单元采用非线性刚度,当船舶与码头距离小于一定值时,碰垫的反力呈非线性增加,其他情况下Link单元的作用力可以忽略不计。
碰垫的非线性张力T为:
T=k(L-L0)
(11)
式中:L0表示Link的原长,处于L0长度下的Link模块张力为零,L表示Link模块的实际长度。当0≤L≤0.7时,k=10/L;当0.7 环境载荷参数如表2所示。 其中环境载荷方向以E为000°,按照逆时针方向旋转至N为090°。 表2 环境载荷参数 3.1 系泊状态下无动力定位船舶和动力定位船舶数值结果对比 图2中动力定位船舶的目标位置为(67.5,95),观察船舶各自由度的运动可以发现,动力定位船舶的位置和艏摇角波动极小,无动力定位船舶由于未受到船舶侧推器的约束,表现在水平三自由度上运动幅度较大且各自由度之间的耦合作用明显高于系泊状态下的动力定位船舶。x轴方向,由于码头及系泊缆的弹性约束,使得动力定位船舶最终稳定在67±0.05 m处;无动力定位船舶在风、浪、流等外界载荷的作用下,x轴方向位移27次达到58 m(与码头共计发生27次碰撞)。在y轴方向,风、流以及一阶波浪载荷对动力定位船舶的船体作用力为零,动力定位船舶在侧推器的作用下,有效克服了二阶波浪漂移力对船体造成的偏移,因此动力定位船舶最终稳定在95±0.003 m处;无动力定位船舶由于在x轴方向大范围运动,导致了系泊缆有效张力在y轴方向上的不均衡分布,这种有效张力的不均衡加大了x,y轴方向运动的耦合程度,进而造成了包含艏摇角在内的船舶整体运动的不稳定。 图2 系泊状态下船舶水平三自由度运动Fig.2 Vessel horizontal degree of freedom motion under mooring condition 图3为船舶水平三自由度谱密度曲线,对比图中各自由度的谱密度值可知,动力定位船舶的运动谱密度均小于无动力定位船舶。在x轴方向上,无动力定位船舶横荡谱密度的3个峰值呈递增趋势,低频峰值主要分布在0.02 Hz及0.04 Hz,码头-系泊缆对船舶横荡运动的限制,二阶波浪漂移力及风、流载荷是这些低频分量产生的主要原因;而由一阶波浪力(T=12 s)引起的高频峰值位于0.08 Hz处。相比之下,动力定位船舶的横荡谱密度峰值仅位于0.02 Hz一处,且其谱密度远小于对应频率下的无动力定位船舶,这说明在侧推器的作用下,系泊动力定位船舶能够很好地消除横荡方向上由一阶波浪力引起的运动分量。在y轴方向上,无动力定位船舶纵荡谱密度远高于x轴方向的船舶横荡谱密度,且在0.025 Hz处达到峰值,由此可以看出,在二阶波浪力等外界载荷的影响下,不同方向间的运动有着强烈耦合作用,且表现在y轴方向上最为明显。在船舶艏摇谱密度图中,无动力定位船舶分别在0.045 Hz及0.08 Hz处取得峰值,且低频峰值明显大于高频峰值;相比之下,动力定位船舶在该自由度上的谱密度基本为零,由此可见码头-系泊缆及侧推器反力能提供良好的船舶艏摇约束。 图3 系泊状态下船舶水平三自由度谱密度Fig.3 Spectral density of vessel horizontal degree of freedom under mooring condition 图1中,系泊缆绳在几何形状上呈对称分布,其末端有效张力有一定的相似性,因此,这里以船舶尾缆为例,对其末端有效张力的时频特性进行简要分析(图4)。 时域中,无动力定位船舶尾缆末端有效张力呈现出不规则的剧烈变化趋势,这种变化增大了系泊缆绳因张力的突变而断裂的可能性;相比之下,由于侧推器的反向推力作用,使得动力定位船舶尾缆能够保持一定程度的张紧,这种预张力的出现有效地克服了因一阶波浪力而引起的船舶运动。当波浪力(包括二阶慢漂力)与尾缆末端有效张力反向时,尾缆末端有效张力缓慢增加;波浪力与尾缆末端有效张力同向时,尾缆末端有效张力缓慢降低。在0~800 s期间,如图2和图3中所示,动力定位船舶在水平三自由度的运动均保持在极小范围内,这说明通过侧推器的反向推力把船舶在水平三自由度的不规则运动转化为系泊缆绳有效张力在时域内的规则变化。 频域中,无动力定位船舶尾缆末端有效张力谱密度在0.0~0.3 Hz范围内均匀分布,其运动频率组成较为复杂;而动力定位船舶尾缆末端有效张力峰值位于0.08 Hz处,这与波浪频率完全一致。该现象表明,通过侧推器对系泊缆绳施加的预张力有效地抵消了一阶波浪载荷对船体的作用力,从而使得船体的水平三自由度保持在极小的变化范围内。 图4 系泊状态下尾缆有效张力及其谱密度Fig.4 Effective tension and its spectral density of stern line under mooring condition 3.2 系泊动力定位船舶和非系泊动力定位船舶数值结果对比 图5a表示系泊状态下xy平面内动力定位船舶的运动轨迹,其目标位置为(67.5,95),23 s后船舶运动轨迹趋于稳定,箭头表示船舶从-10 s到23 s期间船舶相应时刻下的运动方向,最终稳定在(67.5±0.05,95±0.003)处。图5b同样表示系泊状态下xy平面内动力定位船舶的运动轨迹,但其目标位置设为(64,95),相比于图5a,该状态下船舶趋于稳定状态的时间晚了5 s并最终稳定在(64±2.15,95±0.29)处。图5c表示非系泊状态下xy平面内动力定位船舶的运动轨迹,其目标位置为(67.5,95),相比于系泊状态下动力定位船舶进入稳定状态的时间较晚,其中粗实线部分表示28 s后船舶的运动轨迹,船体位置最终稳定在(67.5±2.9,95±0.09)处。 图5 t=-10 ~800 s期间船舶运动轨迹Fig.5 Trajectory of vessel during t=-10 s to 800 s 图6表示相同环境载荷作用下,动力定位船舶的艏摇角时间曲线。从图6a至6c船舶艏摇角幅度呈递增趋势,对比系泊状态下动力定位船舶和非系泊状态下动力定位船舶的艏摇角可以看出,由于系泊缆索对船舶艏摇方向的约束,使得其角度变化要明显小于非系泊动力定位船舶。 图7为不同系泊状态、不同目标定位点动力定位船舶的运动谱密度曲线。在船舶横荡谱密度曲线中,非系泊动力定位船舶TP(67.5,95)与系泊动力定位船舶TP(64,95)谱密度值基本一致,均在波浪载荷频率处取得峰值,相比之下系泊动力定位船舶TP(67.5,95)的横荡谱密度峰值对应频率大大降低。在船舶纵荡谱密度和艏摇谱密度曲线中,可以清楚地看到系泊动力定位船舶TP(64,95)的谱密度值较高,这说明处于该状态下的船舶在水平三自由度上的运动仍然具有较高的耦合程度,而其余两种状态下的船舶各自由度之间运动的耦合程度较小,由此可知码头-系泊缆对于动力定位船舶的定位性能具有一定的改善能力,但前提是确定优良的目标位置。 图6 不同系泊状态及目标定位点的船舶艏摇角时间曲线Fig.6 Time curve of vessel’s yaw angle under different mooring conditions and target positions 图7 不同系泊状态及目标定位点的船舶水平三自由度运动谱密度Fig.7 Spectral density of vessel horizontal degree of freedom under different mooring conditions and target positions 图8为系泊状态下动力定位船舶尾缆有效张力的时间变化图像及其谱密度曲线,相比于图4中无动力定位船舶,动力定位船舶TP(64,95)的尾缆末端有效张力突变虽有一定程度的改善,其谱密度分布仍然占据较大的频率范围(图8b)。在该状态下的船舶,由于其目标位置选取得不合理,导致系泊缆绳无法时刻保持张紧状态,当波浪载荷将船舶推向码头时,系泊缆中没有足够的预张力抵消波浪对船体的作用力;当波浪载荷、码头碰撞力等外载荷将船舶推离码头时,由于距系泊缆有较大的加速位移,导致缆绳必须产生突变的张力以克服船体的运动。因此合理的目标位置能保证系泊缆的有效张力谱密度峰值分布在接近波浪外载荷频率处。 图8 系泊状态下动力定位船舶尾缆有效张力及其谱密度Fig.8 Effective tension and its spectral density of DP vessel stern line under mooring condition 对比图9中各图可知,非系泊状态动力定位船舶 TP(67.5,95)和系泊状态动力定位船舶 TP(64,95)的船舶侧推器载荷随时间分布基本一致,且载荷变化周期较短。由于控制策略中并未包含限制侧推器最大功率的程序,因此在系泊状态动力定位船舶 TP(67.5,95)的船舶侧推器载荷随时间呈上升趋势。结合图5a分析可知,处于该状态下的船舶于23 s时达到稳定状态,且运动幅度极小,可以预见,若在控制策略中加入最大功率限制,也不会对图5中结果造成任何影响。对比各图可以发现系泊动力定位船舶TP(67.5,95)的侧推器推力变化幅度最小,且在加入功率限制后能保证推力处于一定范围内。 图9 船舶侧推器载荷时间曲线Fig.9 Time curve of vessel’s side thruster load 图10a和10b中,非系泊状态动力定位船舶 TP(67.5,95)和系泊状态动力定位船舶 TP(64,95)的船舶侧推器载荷谱密度峰值均分布在频率较高处,相比之下,图10c中的侧推器载荷谱密度峰值则对应于较低的频率。工程实践中,过高频率的侧推器载荷变化将会给包括侧推器在内的动力定位系统整体带来无法预计的严重损害。因此,从频域方面来说系泊动力定位船舶TP(67.5,95)能降低船舶侧推器的推力变化频率。 图10 船舶侧推器载荷谱密度Fig.10 The spectrum density of vessel’s side thruster load 利用OrcaFlex中弹塑性固体、非线性弹簧阻尼器及凝集质量缆等模块建立了动力定位船舶-码头-缆绳的耦合模型。通过控制算例中研究对象是否为动力定位船舶以及控制研究对象是否处于系泊状态,得出以下结论: (1)系泊状态下,无动力定位船舶各自由度之间的耦合程度较大,频域中水平三自由度运动的谱密度值较高,系泊缆末端有效张力在时域中突变,其谱密度在频域中分布均匀;动力定位船舶系泊缆内的预张力对船舶所受的一阶波浪载荷起到了很好的吸收作用,使得动力定位船舶的不规则运动转化成了系泊缆有效张力的规则变化。 (2)从船舶的定位性能方面来说,系泊动力定位船舶的定位能力并不一定完全优于非系泊动力定位船舶,当目标位置选取不合理时,码头系泊缆预张力的大小无法达到吸收船舶所受的一阶波浪载荷的要求。 (3)在侧推器所受影响方面,对于系泊状态下的动力定位船舶,合理的目标位置将会极大地降低侧推器载荷变化的频率,提高了动力定位船舶侧推器的工作效率,对于耦合系统整体安全能起到一定的积极作用。 [1] ZOU Gang, WANG Lei, LIU Han-lin. Research on the heading control mode of the thruster-assisted mooring system[J]. The Ocean Engineering,2013,31(5):11-17. 邹刚,王磊,刘翰林.锚泊辅助动力定位系统艏向控制模式研究[J].海洋工程,2013,31(5):11-17. [2] ZHANG Bing-fu. Design of combinational station keeping system of mooring and DP position for deep water platform[D].Dalian:Dalian University of Technology,2009. 张炳夫.深水动力辅助锚泊系统联合定位设计研究[D].大连:大连理工大学,2009. [3] TANNURI E A,SAAD A C,MORISHITA H M.Offloading operation with a DP shuttle tanker: comparison between full scale measurements and numerical simulation results[C]//Proceedings of the 8th IFAC conference on manoeuvring and control of marine craft,2009:249-254. [4] WICHERS J, DIJK V. Benefits of using assisted DP for deepwater mooring systems[C]//Offshore Technology Conference,1996. [5] ZHU Jian-xun, SUN Li-ping, LIU Sheng-nan, et al. Time domain simulation of a one line failure for a DP-assisted mooring system[J]. Journal of Marine Science and Application,2014,13(3):321-326. [6] ZHANG Da-peng, ZHU Ke-qiang, YAN Xin-kuan, et al.Dynamic analysis of dynamic positioning system of vessel under different wave directions[J].Journal of Waterway and Harbor,2015,36(4);313-317. 张大朋,朱克强,严心宽,等.不同浪向下船舶动力定位的动力学分析[J].水道港口,2015,36(4):313-317. [7] SONG Lin-feng, SUN Li-Ping, WANG De-Jun. Coupling analysis of stinger-lay barge-pipeline of S-lay installation in deep water[J].Journal of Harbin Engineering University,2013,34(4):415-433. 宋林峰,孙丽萍,王德军.深水S型铺管托管架-船体-管线耦合分析[J].哈尔滨工程大学学报,2013,34(4):415-433. [8] SUN Li-ping, ZHU Jian-xun, AI Shang-mao, et al. Coupling time-domain analysis of dynamic position during S-lay operations[J].The Ocean Engineering,2015,33(4);1-10. 孙丽萍,朱建勋,艾尚茂,等.全耦合S型铺管动力定位时域分析[J].海洋工程,2015,33(4);1-10. [9] ZHANG Da-peng, ZHU Ke-qiang. Dynamic analysis of large ships berthing under combined action of wind, waves and current[J].Navigation of China,2015,38(2):48-52. 张大朋,朱克强.风浪流联合作用下大型船舶靠泊过程动力学分析[J].中国航海,2015,38(2);48-52. [10] CHRIS J. Mixing dynamic positioning with moorings[C]. Dynamic Positioning Conference,2005. [11] DAI Jie, PENG Liang, LI Xi-bin, et al. Determination research on longitudinal wave frequency movement of ship[J].YINGYONG KEJI,1995(4):14-18. 戴捷,彭良,李喜彬,等.船舶纵向波频运动的测定研究[J].应用科技,1995(4):14-18. [12] FENTON J D. A high-order cnoidal wave theory[J].J Fluid Mech,1979,94(1):129-161. Time-frequency analysis of wharf-cables-DP vessel coupling system LIU Jian, ZHU Ke-qiang*, BAO Xiong-guan, ZHANG Da-peng (FacultyofMaritimeandTransportation,NingboUniversity,Ningbo315211,China) In order to research the coupling interaction among mooring dynamic positioning vessel, wharf and cables, lumped mass method was used to calculate the effective tension, and nonlinear reaction force of dock fenders was simulated by Link unit in OrcaFlex. The thrust allocation of thrusters was based on PID control system. Under mooring conditions, with the comparison the difference in horizontal degree of freedom motion and cable’s effective tension between general vessel and dynamic positioning vessel, the effect of thrusters on eliminating ship movement caused by first order wave loads has been explained. According to the results of mooring DP vessel and DP vessel in the same environment load, the influence of wharf-cable and target position on side thrusters and positioning ability were discussed. The results show that the performance of the side thrusters and vessel’s positioning capability can be improved effectively under the reasonable selection of target position. dynamic positioning; first-order wave load; coupling system; time-frequency characteristics 10.3969/j.issn.1001-909X.2017.02.005. 2016-04-29 2017-01-20 国家自然科学基金项目资助(11272160);浙江省自然科学基金项目资助(LY13A020006);国家自然科学基金青年项目资助(51309133) 刘建(1991-),男,安徽亳州市人,助理研究员,主要从事船舶与海洋工程结构物动态响应方面的研究。E-mail:275645569@qq.com *通讯作者:朱克强(1956-),男,教授,主要从事船舶与海洋工程结构物动态响应方面的研究。E-mail: zhukeqiang@nbu.edu.cn U664.82 A 1001-909X(2017)02-0044-09 10.3969/j.issn.1001-909X.2017.02.005 刘建,朱克强,包雄关,等.码头-缆绳-动力定位船舶耦合系统的时频特性分析[J].海洋学研究,2017,35(2):44-52, LIU Jian, ZHU Ke-qiang, BAO Xiong-guan, et al. Time-frequency analysis of wharf-cables-DP vessel coupling system[J].Journal of Marine Sciences,2017,35(2):44-52,doi:10.3969/j.issn.1001-909X.2017.02.005.3 数值结果与分析
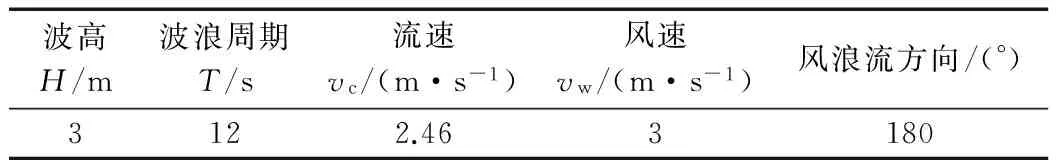
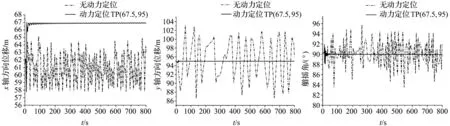





4 结论
