带干扰的切换双机电力系统鲁棒控制器设计

陈胜泉，孙丽颖

（辽宁工业大学 电气工程学院，辽宁 锦州121001）

带干扰的切换双机电力系统鲁棒控制器设计

陈胜泉，孙丽颖

（辽宁工业大学 电气工程学院，辽宁 锦州121001）

针对带干扰及系统参数不确定励磁控制的切换双机电力系统的鲁棒控制器设计问题,首先建立系统的数学模型，然后利用公共Lyapunov函数方法和H∞控制，实现系统切换控制器的设计,得到了带干扰切换双机电力系统在任意切换下的渐近稳定性的结果。因而，电力系统中遇到紧急情况需要退出或者增加1台发电机时，该切换过程系统都保持稳定，并通过仿真进行了验证。

双机电力系统；切换系统；公共Lyapunov函数；H∞控制

电力系统是由发电机组、变电所、电力负荷、输电线路以及不同等级的电力网络所组成的十分庞大而复杂的动力学系统。而切换系统也是动态系统中极其重要的一种类型，在电力系统中，引入切换控制既实现系统的稳定性又改善了系统的暂态响应。文献[1-2]针对多机电力系统，应用非线性鲁棒控制原理设计控制器，从而实现多机电力系统的分散协调控制。文献[3-4]利用发电机组的励磁和汽门系统相结合,加大系统的阻尼系数,减少系统的振荡次数,设计出最优控制器。文献[5]针对参数确定和参数不确定的切换双机电力系统进行了稳定性分析，通过公共Lyapunov函数方法验证了其稳定性。文献[6]建立了IEEE三机互联电力系统的切换控制数学模型，通过预置状态反馈完成了系统的耗散Hamilton函数[3]，实现并设计了切换励磁控制器，并利用多Lyapunov函数证明了闭环系统在任意切换路径下的渐近稳定性。文献[7-8]基于切换控制率，建立一个切换双机系统，将系统转化为切换Hamilton系统，对系统进行分析，从而使系统达到稳定。文献[9-10]利用模糊控制方法对切换动态系统进行了鲁棒性分析，得出在任意切换下的系统都是稳定的。

但是上述文献都没有考虑有干扰的情况,在电力系统中必不可少地存在电磁干扰和机械干扰，因此考虑了带干扰的情况，更精确地联系了实际情况。首先对带参数不确定的切换双机电力系统建立数学模型，利用公用Lyapunov函数方法[11]，给出切换双机电力系统的切换率，结合自适应逆推方法设计控制器，设计的控制器满足闭环系统在任意切换路径下的渐近稳定，最后仿真结果验证所设计的控制器的有效性。

1 切换双机电力系统的动态模型

针对由2台发电机组组成的电力系统，图1为切换双机电力系统结构图[12]。

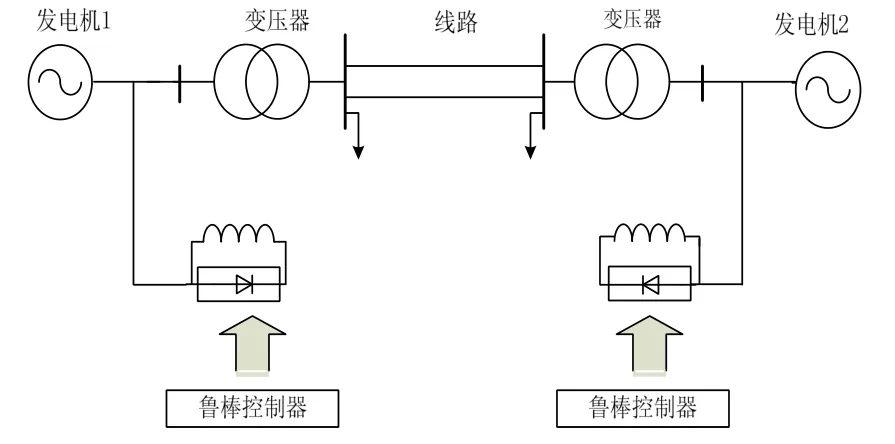
图1 切换双机电力系统

则可建立具有励磁控制的双机电力系统的数学模型[4]：

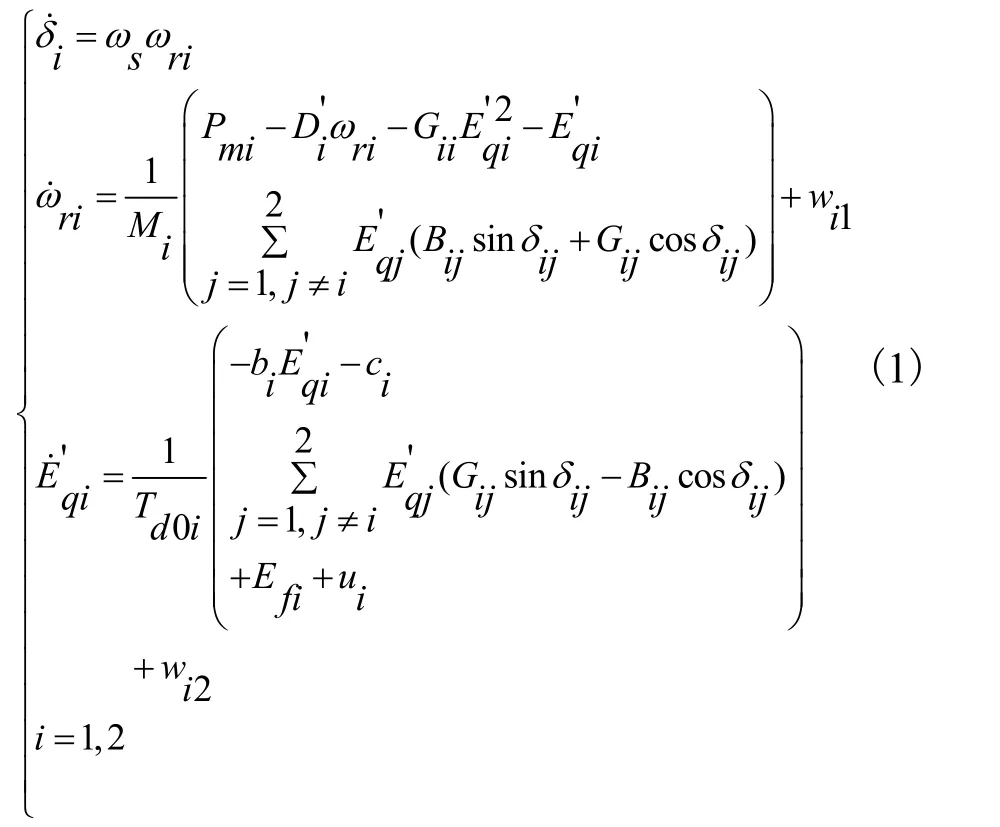
其中：

针对图1所示的双机电力系统，当遇到紧急情况时，需要退出或者增加1台发电机来平衡系统的有功、无功以及电压，使整个双机电力系统都在稳定运行状态。首先，建立双机电力系统的切换模型，根据上述紧急控制原理，设计切换率，得到3个子系统模型[5]。

子系统1，当2号发电机从系统退出时：

子系统2，当1号发电机从系统退出时：

子系统3，当1，2号发电机同时运行时：

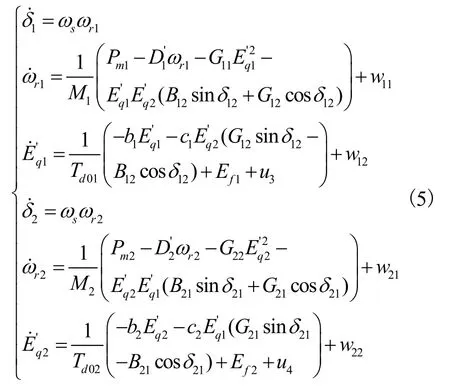
2 控制器设计

首先对子系统1、2、3构造如下形式的公共Lyapunov函数：

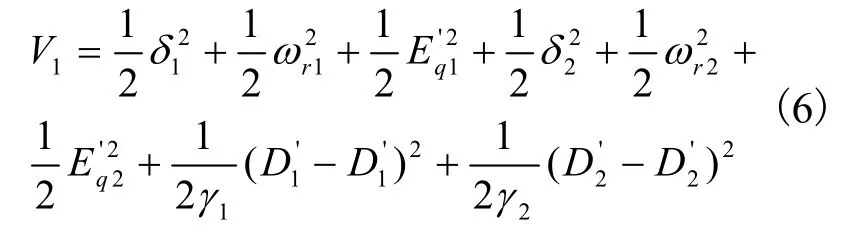
对于子系统1，V对时间的导数：

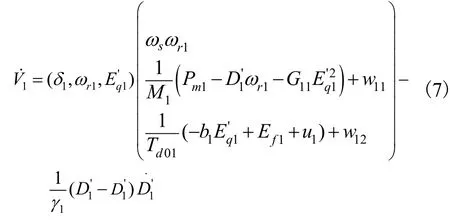
将子系统1选择调节输出：

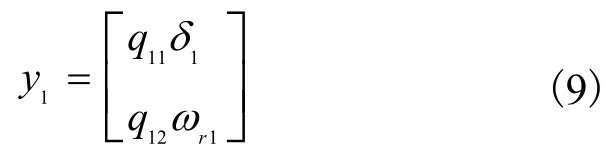
则子系统1的状态方程可描叙为：

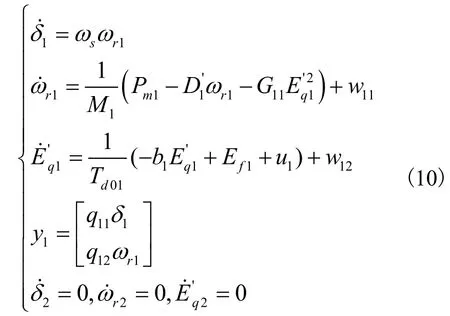
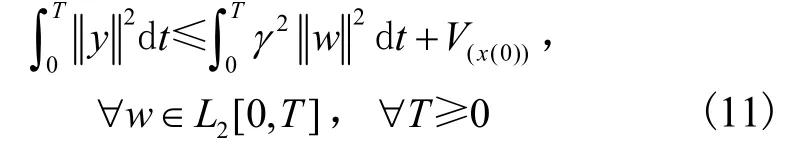
其中，V(⋅)是需要构造的系统能量存储函数，x(0)是初始状态，是外部干扰[14]。对式(7)求导得到函数：

定义函数：

控制目标在考虑外部干扰的情况下将自适应控制与H∞控制方法结合对切换双机电力系统的励磁设计鲁棒H∞控制器，设计过程中通过构造系统的存储函数V(x)推导出耗散不等式：

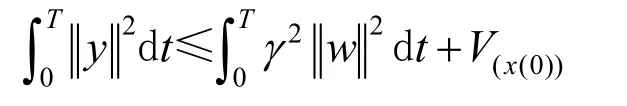
成立，得到系统的干扰对输出的影响小于干扰衰减常数γ[15]。

对于子系统1，定义函数H1，只要满足H1≤0，则耗散不等式成立。

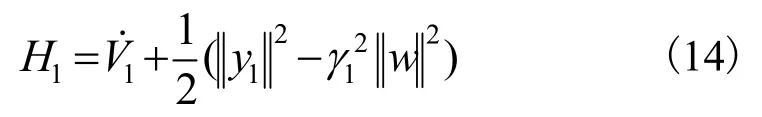
当

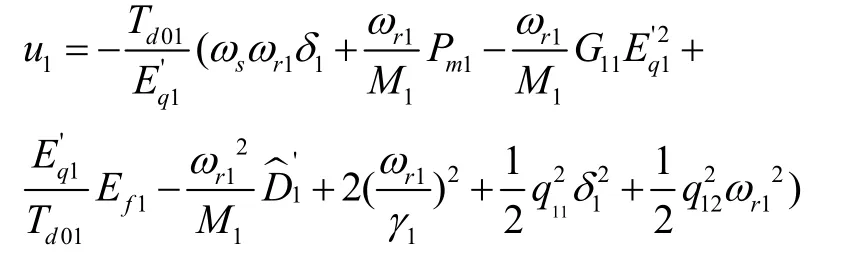
时，将u1带入式(14)中得：

此时子系统1存储函数V(x)最终推导出耗散不等式：

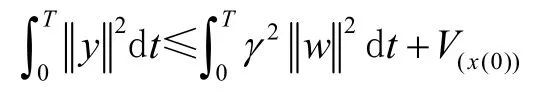
成立，得到系统的干扰对输出的影响小于干扰衰减常数γ。使得双机电力系统的状态变量最终收敛到一个很小的领域内，从而使系统达到稳定的状态。

同样，对于子系统2，选择调节输出：

对于子系统3，选择调节输出：

其中q31≥0，q32≥0，q33≥0，q34≥0，同样也要满足。分别使H2≤0，H3≤0。

由子系统1、2、3的存储函数V(x)最终推导出耗散不等式：

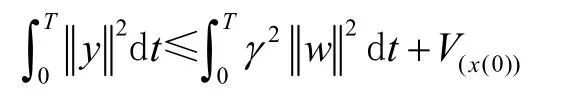
成立，得到系统的干扰对输出的影响小于干扰衰减常数γ。使得双机电力系统的状态变量δ、ω、最终收敛到一个很小的领域内，从而使系统达到稳定的状态。

3 切换律设计

为实现系统在任意时刻的切换，对本系统控制率进行了设计。系统在前25 s是正常运行，25 s时系统发生紧急故障，需要增加1台发电机才能使系统达到平衡。在50 s后系统故障切除，运行1台发电机。这种情况也适用于当1台发电机需要检修而又不影响供电时的情况。则切换控制率如下：

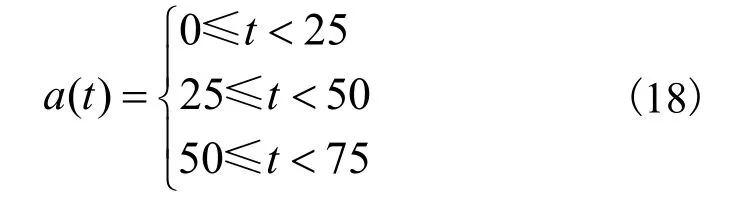
4 仿真研究

对切换双机电力系统进行Matlab仿真分析。

发电机G-1参数：

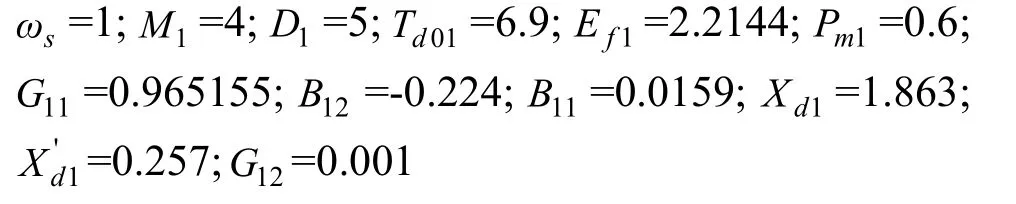
发电机G-2参数：

根据上述控制律设计的仿真如图2、图3所示。

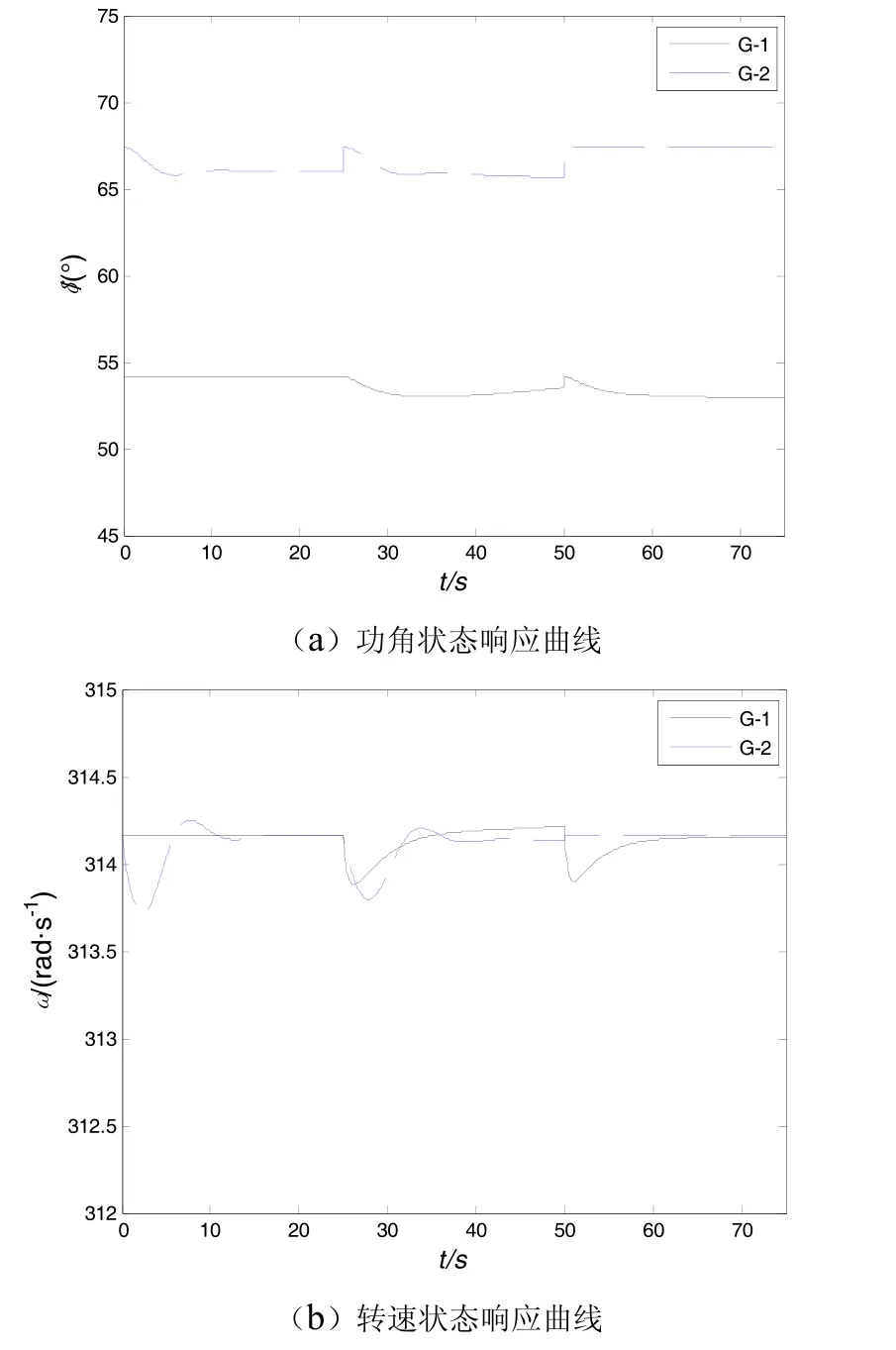
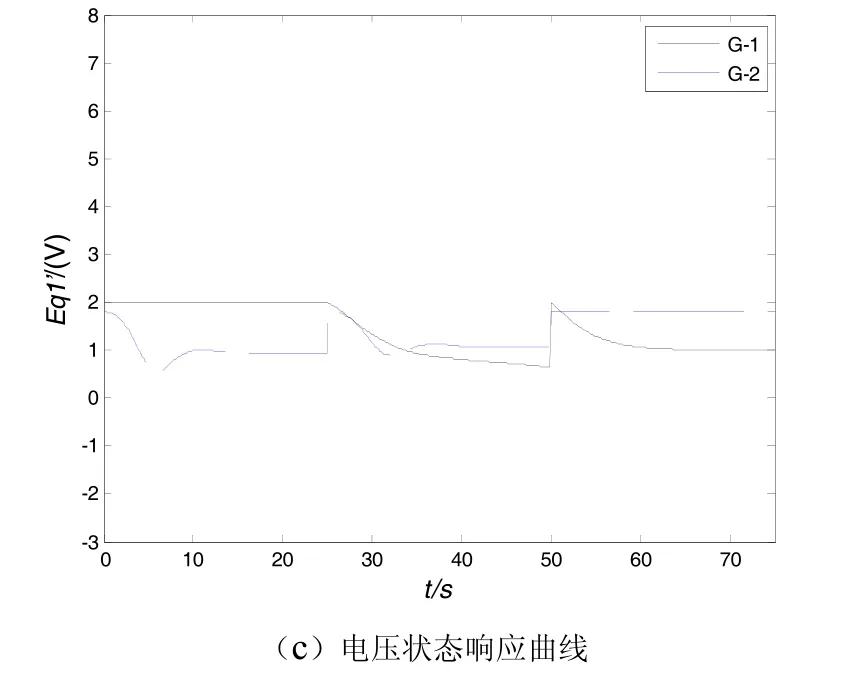
图2 切换双机电力系统发电机的状态响应曲线

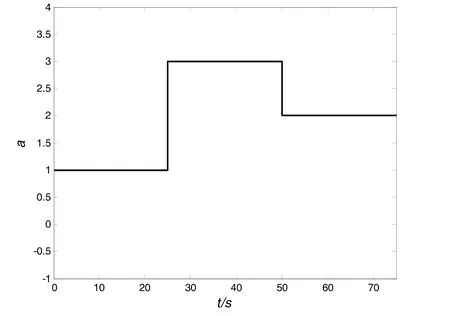
图3 切换信号

5 总结

本文考虑了带干扰下的双机电力系统的稳定性分析，主要研究在故障情况下双机电力系统的切换稳定问题，结合切换控制规则，利用公共Lyapunov函数使切换双机电力系统达到稳定，通过H∞控制使系统的控制目标δ,ω,收敛于一个很小的领域内，仿真分析证明了结果的可行性。

[1]严姝,孙元章,黎雄.多机电力系统分散鲁棒励磁控制器的研究[J].电力系统自动化,2004,24(22):21-38.

[2]蔡静雯,孙丽颖.多机电力系统汽门开度直接模糊Backstepping控制[J].辽宁工业大学学报:自然科学版, 2014,34(6):351-355.

[3]刘梦欣.多机电力系统励磁和广义Hamilton实现控制方法与应用[D].上海:上海交通大学,2008.

[4]林丽君.汽轮发电机励磁与汽门协调控制器设计[D].保定:华北电力大学,2012.

[5]冯泉.切换双机电力系统的稳定性研究[D].沈阳:东北大学,2009.

[6]徐利梅,王玉,曹纪烈.切换双机电力系统的鲁棒控制器设计[J].西南民族大学学报:自然科学版,2014, 40(1):115-119.

[7]ZHU Li-ying,WANG Yu-zhen.Study on the stability of switched dissipative Hamiltonian systems[J].Science in China,2006,49(5):578-591.

[8]Zhu L,Wang Y.On the modeling and stability analysis of switched two-machine power systems[C].Intelligent Control and Automation,2008.WCICA 2008.7th World Congress on.IEEE,2008:719-7197

[9]景丽,高立群,刘罗曼.基于模糊方法的切换系统稳定性研究[J].自动化技术与应用,2007,26(10):1-3.

[10]Sun Z,Ge S S.Stability Theory of Switched Dynamical Systems[M].London:Springer-Verlag,2011.

[11]马国梁,陈庆伟,胡维礼.基于公共Lyapunov函数的一类切换系统H∞鲁棒控制[J].系统工程与电子技术,2006(7): 1043-1045.

[12]卢强,梅生伟,孙元章.电力系统非线性控制[M].北京:清华大学出版社,2008.

[13]兰洲,甘德强,倪以信.电力系统非线性鲁棒自适应分散励磁控制设计[J].中国电机工程学报,2006,26(17):1-5.

[14]梅生伟,申铁龙,刘康志.现代鲁棒控制理论与应用[M].北京:清华大学出版社,2008

[15]滕波.电力系统自适应鲁棒H∞控制[D].沈阳:东北大学, 2009.

责任编校：孙 林

Robust Controller Design for Switched Two-machine Power System with Disturbance

CHEN Sheng-quan,SUN li-ying

（Electrical Engineering College,Liaoning University of Technology,Jinzhou 121001,China）

For systems with uncertain parameters with interference and robust controller design problem excitation control switch dual-power system,first,the mathematical model is established,and then,by using public Lyapunov function andH∞control,the result of the asymptotic stability of the switched two-machine power system with the disturbance is obtained.Thus,when to exit is needed or a generator is added in the event of an emergency situation in the power system,the whole switching system is stable and it is verified by simulation.

two-machine power system;switching system;public Lyapunov function;H∞control

TM761

A

1674-3261(2017)01-0006-04

2015-11-12

辽宁省自然科学基金项目(2015020076)

陈胜泉(1989-)，男，湖南湘潭人，硕士生。

孙丽颖(1972-)，女，辽宁抚顺人，教授，博士。

10.15916/j.issn1674-3261.2017.01.002