基于backstepping的多机电力系统SVC自适应滑模控制

赵 岩，孙丽颖

（辽宁工业大学 电气工程学院，辽宁 锦州121001）

基于backstepping的多机电力系统SVC自适应滑模控制

赵 岩，孙丽颖

（辽宁工业大学 电气工程学院，辽宁 锦州121001）

针对含SVC的两区域互联多机电力系统，将其等值为两机系统，基于backstepping方法，结合自适应控制和滑模控制，设计一种非线性鲁棒SVC控制器。在backstepping的每一步都设计范数型滑模项补偿不确定性，并采用自适应控制对未知上界进行估计，从而有效地避免了“系数膨胀”问题。同时，考虑系统受到的外部扰动，用自适应控制实现对扰动上界的估计，使控制器具有强鲁棒性。仿真结果表明，所设计的SVC控制器明显提高了跨区域互联电力系统的稳定性。

自适应控制；backstepping方法；滑模控制；SVC；多机电力系统

全国电网互联虽然带来了许多好处，但是由于输电网络的不断扩大，以及输电容量、电压等级的不断提高，电力系统的稳定运行问题也日益严重[1]。随着电力电子技术的快速发展，静止无功补偿器（SVC）已经在电力系统中广泛使用。因此，设计一种更合理且有效的SVC控制器，把它应用在电力系统稳定控制中，是一个值得研究的课题。近年来，许多控制方法被应用于设计SVC控制器，主要集中于构造Hamilton函数方法[2-3]、L2增益干扰抑制[4-5]、backstepping[6-7]、滑模控制[8]等。

Backstepping方法是一种逆向递推设计的控制理论，通过反步递推每个子系统相对应的反馈控制律，实现对整个非线性系统的镇定。因为电力系统中含有不确定参数，需要设计具有自适应功能的控制器，所以把自适应控制和backstepping方法相结合设计控制器。文献[4,6-7]基于自适应backstepping方法设计SVC控制器，但是，都忽略了backstepping方法的“系数膨胀”问题。为解决“系数膨胀”问题，学者们也做了很多研究，包括动态面控制[9-10]、采用非线性跟踪微分器[11-12]、自适应滑模控制[13-14]等。其中，文献[13]提出的自适应滑模控制方法具有很大优势，不仅控制器设计过程简单，而且鲁棒性强。

本文针对含SVC的多机电力系统，在考虑阻尼系数的不确定性和系统受到外部扰动的条件下，基于backstepping方法，结合自适应控制和滑模控制，设计SVC的非线性鲁棒控制器。在设计过程中，设计了阻尼和外部扰动上界的自适应估计律，使控制器具有强鲁棒性。最后，选择两区域4机电力系统[15]进行仿真，仿真结果展示了所设计的控制器的有效性和优越性。

1 系统模型

装有SVC的两区域互联电力系统如图1所示，SVC装在联络线的中间位置，这样可以最大程度地发挥SVC的控制效果[8]。为了研究方便，可以像文献[16]一样，将其等值为两机系统（如图2所示），图中G1、G2为等值发电机。

图1 含SVC的两区域互联系统

图2 含SVC的等值两机系统

发电机采用暂态电抗使暂态电势恒定，并令输入机械功率不变，考虑系统阻尼，则系统的数学模型为：

式中：i=1,2；δi为等值发电机的转子运行角，rad；ωi为等值发电机的转子角速度，rad/s；Hi为等值发电机的转动惯量，s；Di为等值发电机的阻尼系数；Pmi为原动机输入机械功率；Pei为等值发电机的电磁功率；ωi为等值发电机的额定转子角速度，rad/s；其他无特殊说明的单位均为标幺值。

在不考虑负荷的功率以及线路的损耗时，发电机的电磁功率为：

其中，Xac为交流联络线上的总电抗，BSVC是SVC的电纳，

将SVC等效为一阶惯性环节，则SVC数学模型为：

其中，BSVC0为SVC的电纳初始值，T为SVC惯性时间常数，u为SVC的控制量。

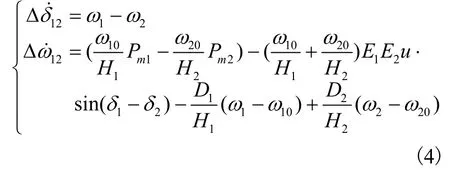
假设系统阻尼是均匀的[17]，令，则系统(4)中的不确定部分转化为：

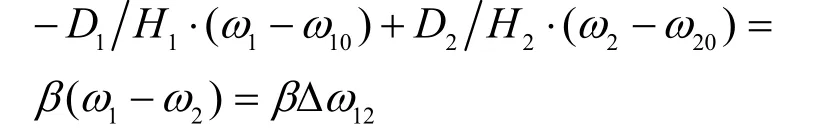
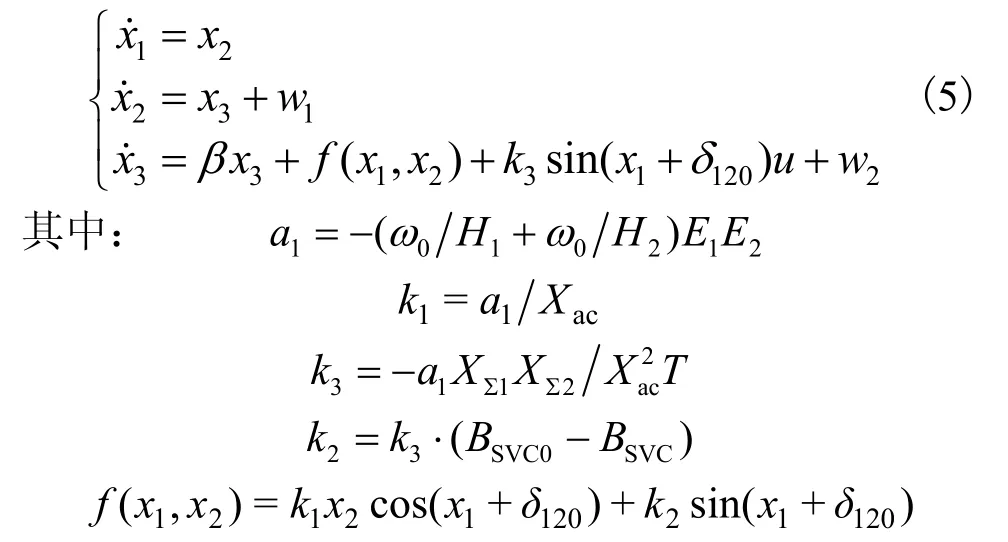
控制目标：综合考虑阻尼系数的不确定性和不确定未知外部干扰，设计SVC的非线性鲁棒控制规律，以调节发电机的相对功角和相对转速在稳定状态运行。

2 控制器设计

对于系统(5)，其中包含不确定参数和外部扰动，基于backstepping方法进行控制器的设计。因为系统(5)是一个三阶的系统模型，所以控制器设计分3步进行。

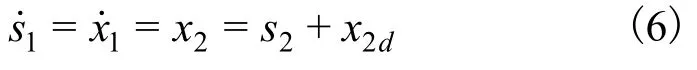
把x2视为虚拟控制量，取镇定函数为：

由式(6)可知，s2与状态变量x2有关，不容易计算，根据文献[13]把s2看作不确定项，并做假设如下。

假设1[13]令，其中α1是未知且有界的正常数。

为补偿s2的不确定性，设计函数为：

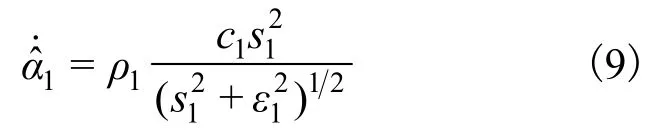
取第一阶的Lyapunov函数为：

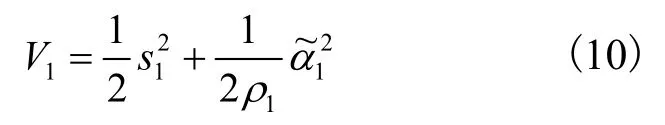
则V1关于时间的导数为：

当s1满足时，有：

由式(12)可以看出，该式中不含有耦合项s1s2，从而避免了“系数膨胀”。

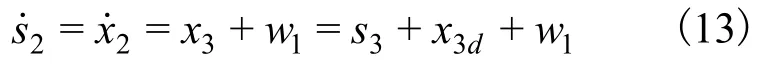
把x3视为虚拟控制量，取镇定函数为：

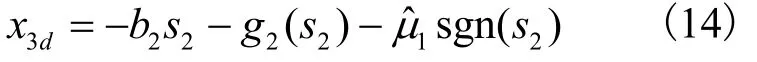
由式(13)可知，s3与状态变量x3有关，同理做假设如下。

假设2[13]令，其中α2是未知且有界的正常数。

为补偿s3的不确定性，设计函数为：

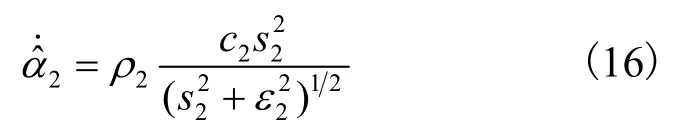
因式(13)中包含外部干扰w1，设计其上界μ1的自适应估计律为：

增广V1，形成前两阶的Lyapunov函数为：

则，V2关于时间的导数为：

当滑模面s2满足时，有：

同理，式（20）中也不含有耦合项s2s3，避免了“系数膨胀”。

第三步：针对系统（5）的第三阶。首先，对s3的求导为：

假设3[13]令，其中α3是未知且有界的正常数。

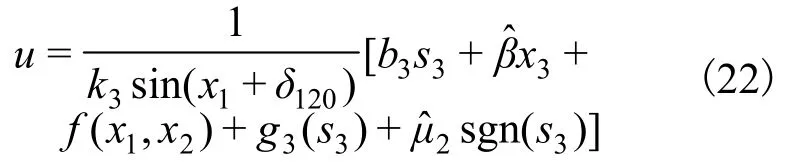
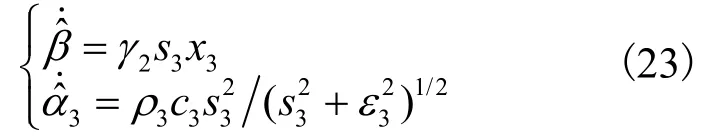
因式(21)中包含外部干扰w2，设计其上界μ2的自适应估计律为：

增广V2，得到全系统的Lyapunov函数为：

则，V关于时间的导数为：

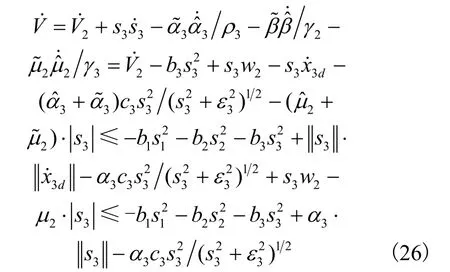
当滑模面s3满足时，有：

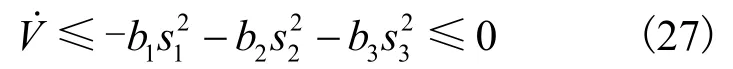
因此，在反馈控制律(22)作用下，闭环系统的误差滑模面动态为：

由LaSalle’s定理[18]可知：对于系统(5)，在反馈控制律(22)和自适应估计律(9)、(16)、(17)、(23)和(24)共同作用下，闭环系统(28)在平衡点附近是渐近稳定的，即。当t→∞时，，，，。由x1，x2，x3，x2d，的定义可知，，x3也是有界的。

3 仿真研究

针对图3所示的两区域四机电力系统[15]，使用MATLAB软件进行仿真。发电机的参数见文献[15]，仿真参数为：δ130=15°，c1=c2=c3=2，b1=b2=b3=2，ρ3=15，γ1=γ2=γ3=ρ1=ρ2=1，ε1=ε2=ε3=0.05。

图3 含SVC的两区域四机系统

仿真情况1：假设在t=0 s时，系统功角差偏离平衡点5°，此时功角差的初始值为20°。仿真结果见图4和图5。

仿真情况2：假设系统在t=0～0.5 s处于稳定运行状态，突然在t=0.5 s时，输电线路上发生三相短路故障，在t=0.6 s时，切除故障。仿真结果见图6和图7。

图中，实线是本文控制方法(AbSM)所得波形，虚线是自适应backstepping方法(Ab)所得波形。

因为SVC被装于Area1和Area2之间的联络线上，并且发电机G1和G2以及G3和G4的参数一样，所以G2相对于G4的响应曲线与图4～图7类似，在此不再给出。

从图4和图5可以看出，当系统功角差偏离平衡点5°时，采用本文的控制策略(AbSM)时，发电机G1和G3的相对功角和相对转速在1.5 s左右就能恢复稳定状态。相比之下，当采用自适应backstepping方法(Ab)时，系统恢复稳定的速度较慢，需要的时间较长，大约需要2.5 s左右。

从图6和图7可以看出，在0.5 s时，输电线路突然发生三相短路故障，所设计的SVC控制器立刻对系统进行操作，在2 s时，系统回到了原来的稳定状态。相对于自适应backstepping方法(Ab)，本文方法可以使系统快速切除故障，振荡范围小，暂态性能较好。

图4G1相对于G3功角响应曲线

图5G1相对于G3转速响应曲线

图6G1相对于G3功角响应曲线

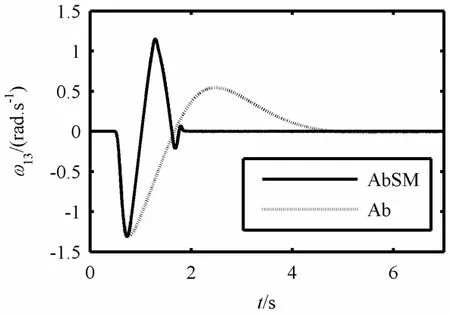
图7G1相对于G3转速响应曲线

4 结论

针对含SVC的两区域互联多机电力系统，对其进行简化，等值为两机系统。在综合考虑系统受到内外部干扰的情况下，基于backstepping方法，结合自适应控制和滑模控制，设计一种非线性鲁棒SVC控制器。在backstepping设计过程中，采用自适应控制和滑模控制避免“系数膨胀”问题。对于阻尼系数，用自适应控制设计其自适应估计律，使其具有自适应能力。对于外部扰动，采用滑模控制设计不连续滑模项对其进行补偿，并结合自适应控制实现对滑模项参数的实时估计。仿真结果表明，所设计的SVC控制器具有强鲁棒性，明显改善了跨区域互联电力系统的稳定性。

[1]邹强,李兴源.基于最优变目标策略的励磁系统与SVC协调控制[J].电网技术,2006,30(10):24-28.

[2]刘孙贤,张敏,钟义长,等.基于Hamilton能量函数含SVC的电力系统非线性控制[J].电力系统及其自动化学报,2006,18(4):24-28.

[3]刘艳红,宋伟华,王杰.包含SVC和非线性负荷的电力系统耗散实现与控制[J].控制理论与应用,2010,27(1): 47-52.

[4]陈娇英,李啸骢,李文涛,等.基于自适应Backstepping的SVC鲁棒L2性能控制设计[J].电力系统保护与控制, 2011,39(17):40-44,69.

[5]张蕾,张爱民,韩九强,等.基于系统浸入和流形不变自适应方法的静止无功补偿器非线性鲁棒自适应控制方法[J].控制理论与应用,2013,30(1):1-7.

[6]付俊,赵军,乔治·迪米罗夫斯基.静态无功补偿器鲁棒控制的一种新自适应逆推方法[J].中国电机工程学报, 2006,26(10):7-11.

[7]SunLiying,TongShaocheng,LiuYi.Adaptive Backstepping Sliding ModeH∞Controlof Static Var Compensator[J].IEEE Transactions on Control system Technology,2011,19(5):1178-1185.

[8]王曦,王渝红,李兴源,等.考虑模型不确定性和时延的静止无功补偿器自适应滑膜控制器设计[J].物理学报, 2014,63(23):428-435.

[9]周丽,姜长生.改进的非线性鲁棒自适应动态面控制[J].控制与决策,2008,23(8):938-943.

[10]方一鸣,许衍泽,李建雄.具有输入饱和的电液伺服位置系统自适应动态面控制[J].控制理论与应用,2014, 31(4):511-518.

[11]胡云安,晋玉强,查旭,等.BTT导弹块模型的鲁棒自适应设计[J].宇航学报,2004,25(2):225-230.

[12]甄红涛,齐晓慧,夏明旗,等.四旋翼无人机鲁棒自适应姿态控制[J].控制工程,2013,20(5):915-919.

[13]朱凯,齐乃明,秦昌茂.BTT导弹的自适应滑模反演控制设计[J].宇航学报,2010,31(3):769-773.

[14]王芳,宗群,田栢苓,等.基于鲁棒自适应反步的可重复使用飞行器再入姿态控制[J].控制与决策,2014, 29(1):12-18.

[15]Kunder P.Power system stability and control[M].New York:McGraw-Hill,1994.

[16]赵振元,陈维荣,戴朝华,等.系统惯性时间常数对互联电网暂态稳定水平的影响[J].电网技术,2012,36(1): 102-107.

[17]倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.

[18]Khalil H K.Nonlinear system[M].Third Edition.Beijing: Publishing House of Electronic Industry,2011.

责任编校：孙 林

Adaptive Sliding Mode Control for Multi-machine Power System SVC Based on Backstepping

ZHAO Yan,SUN Li-ying
（Electrical Engineering College,Liaoning University of Technology,Jinzhou 121001,China）

For the Multi-Machine power system with SVC,it is equivalent to the two-machine system.Based on the backstepping methods and combination of the adaptive control and the sliding mode control,a novel nonlinear robust controller is designed.In each step of the backstepping method, a norm sliding mode term is designed to compensate for the uncertainties of the system.The adaptive control is used to estimate the unknown upper bound.In this way,the problem of“coefficient expansion”is avoided effectively.At the same time,considering the external disturbance of the system, the estimation of the upper bound of the disturbance is realized by the adaptive control,which makes the controller have strong robustness.The simulation results show that the designed SVC controller can improve the stability of the interconnected power system.

adaptive control;backstepping method;sliding mode control;SVC; multi-machine power system

TP311

A

1674-3261(2017)01-0001-05

2016-04-20

辽宁省自然科学基金项目(2015020076)

赵 岩(1992-)，男，河北迁安人，硕士生。

孙丽颖(1972-)，女，辽宁抚顺人，教授，博士。

10.15916/j.issn1674-3261.2017.01.001