基于CFD的转轮叶片对虹吸式水轮机水力性能的影响分析

俞芸芸,秦战生,周大庆,刘 敏

(河海大学能源与电气学院,江苏 南京 210098)

基于CFD的转轮叶片对虹吸式水轮机水力性能的影响分析

俞芸芸,秦战生,周大庆,刘 敏

(河海大学能源与电气学院,江苏 南京 210098)

为了更加高效地利用超低水头水力资源,设计了一种采用虹吸式出水流道的轴流式水轮机。针对这一形式的水轮机,在设计水头和额定转速下采用CFD进行三维数值模拟,计算各过流部件的水力损失,研究水轮机的水力性能。通过改变转轮叶片出水边翼形,对比分析转轮出口水流流态与虹吸式出水流道水头损失的关系,研究不同叶片对虹吸式水轮机水力性能的影响。结果表明,在水头、转速和导叶开度相同的情况下,各修改方案中叶片3使得出水流道水头损失较小,其对应的平均涡角为13.26°,出水流道水头损失为0.135 m,水轮机的效率也较高(为89.33%)。此外,选取效率较高的叶片,改变叶片数量,分析其对虹吸式水轮机水力性能的影响。

虹吸式水轮机;出水流道;叶片;涡角;水力损失

我国拥有丰富的水力资源,其中高水头水力资源主要集中分布于西南等偏远地区。在华东、中南等沿海地区,工农业生产发达,用电需求量增长较快,该地区中、高水头水力资源已开发殆尽[1],而低水头水力资源较为丰富,电力输送具有不可比拟的优越性,其开发价值更具吸引力[2]。目前低水头电站开发面临的最大问题是相同出力下机组尺寸较大,土建工程量大,单位造价高。从运行角度看,目前大多采用的全贯流水轮机和灯泡贯流水轮机机组并不完全适用于超低水头段运行,勉强使用会带来运行效率低、噪音大、易气蚀、寿命短等问题[3]。因此,为了解决我国水力资源开发面临的问题,开发建设投资少、工期短、水力资源分散的低水头小尺寸水轮机成为可再生能源开发利用的重点[4]。

传统水电站的出水流道常采用弯肘型和直锥型尾水管,这2种尾水管都属于尾水管下置的配置方式,常伴随着较大的土建开挖量,需要较大的前期投资[5]。笔者利用虹吸原理设计了虹吸式出水流道[6],并将其安装于已有挡水建筑物外侧,可以使水轮机结构简单,尺寸较小,安装方便,能较好地保证水流流态,有效利用低水头资源,减少不必要的土建投资,避免厂房的大量建设投入。

我国已建的大型泵站中不少采用了虹吸式出水流道[7-8],但将其应用在水轮机上的研究相对较少。笔者采用CFD数值模拟设计了一种效率较高的设计水头为2 m的虹吸式水轮机,分析转轮出口水流流态对出水流道及水轮机水力性能的影响,对比确定了较优的叶片,得到效率较高的虹吸式水轮机装置,实现了低水头水力资源的高效利用,为今后类似水轮机的设计和优化提供参考。

1 数值计算模型和方法

1.1 模型基本参数

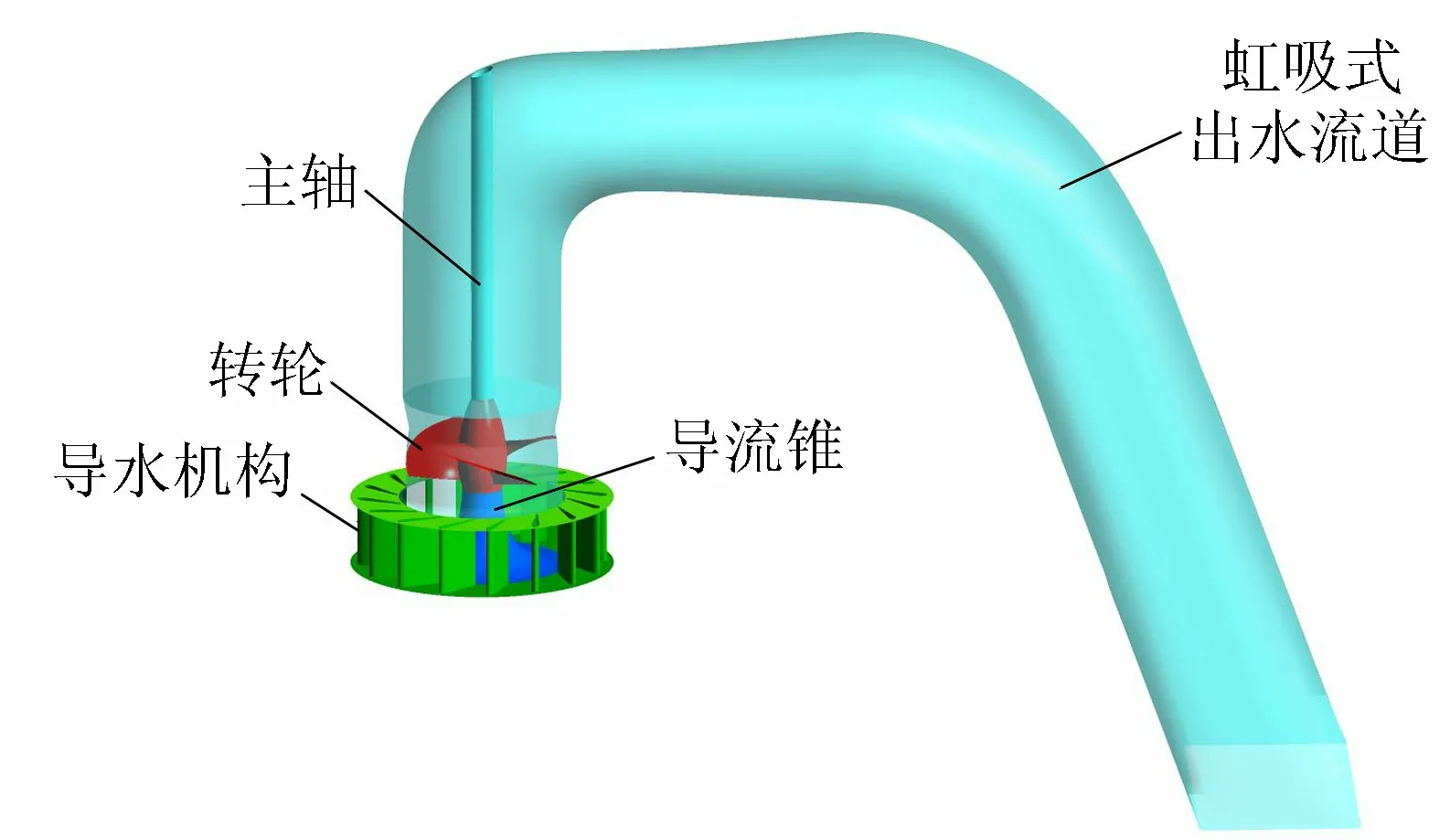
图1 虹吸轴流式水轮机模型Fig.1 Siphon axial-flow turbine model

虹吸轴流式水轮机由含有16个活动导叶的导水机构、3个叶片的转轮和虹吸式出水流道构成,模型的主要参数如下:转轮直径D=1.0 m,设计水头Hr=2.0 m,转速n=195 r/min。图1为开发设计的虹吸轴流式水轮机模型。

1.2 计算方法

虹吸轴流式水轮机的内部是介质为水、不可压缩的黏性湍流流动,数值计算控制方程采用不可压缩的连续方程和三维定常雷诺时均Navier-Stokes方程[9]求解,方程如下:

(1)

(2)

式中:ui——i方向流速的瞬时值;xi——坐标;ρ——流体密度;p——流体压力;Fi——质量力在i方向的分量;μ——运动黏度。

湍流模型采用Spalart-Allmaras模型,该模型属于一方程模型,计算量较小、计算精度较高,克服了两方程模型计算量大且收敛困难的问题[10],能更好地模拟虹吸式水轮机内的复杂流场。为提高计算精度和稳定性,计算中对流项采取二阶迎风格式[11],隐式求解,压力项和扩散项采用中心差分格式。湍流流场的压力-速度耦合方程求解采用SIMPLEC算法,此算法较SIMPLE算法收敛更快[12]。计算过程中通过监测残差值是否达到设定精度和监控转矩是否稳定平衡来判断其收敛性。

1.3 计算域及网格划分

虹吸式水轮机计算域包括导水机构、导流锥、转轮和出水流道4个部分,为了保证模型数值模拟的精确性,对初始模型多次用Gambit和ICEM进行非结构化和结构化网格划分,通过FLUENT计算得到结果,验证网格无关性,选取网格单元数量分别为109.5×104个、81.3×104个、60.7×104个、14.1×104个,共计265.6×104个。其中转轮区域流体采用相对旋转坐标系的方法,其他区域流体定义在静止坐标系下。在计算过程中,壁面处的流速、压力等物理量变化较剧烈,对边界层网格进行了多层次划分,将固壁边界设定为绝热无滑移边界条件[13],计算区域采用交界面interface连接。因转轮和导叶部分结构较复杂,对这两部分网格进行局部加密以提高计算精度。忽略转轮室与转轮叶片缘之间的间隙流动,将进水流道的进口设置为压力进口,总压设为19 620 Pa,给定出水流道的出口相对静压为0 Pa。

2 虹吸式水轮机数值模拟计算

2.1 初始模型计算

对初始虹吸式水轮机模型进行数值模拟计算,流量为2.745 m3/s,出力为41.45 kW,水轮机效率为81.19%。对模型各部件的水力损失进行计算,导水机构的水头损失为0.013 m,导流锥的水头损失为0.019 m,转轮的水头损失为0.121 m,出水流道的水头损失为0.201 m。

根据计算结果可知,水轮机的转轮和出水流道部分水力损失较大,需要分析虹吸式这一特殊出水流道内的水流流态,以及转轮出口水流对出水流道损失的影响,改变出水流道的进口水流流态来降低其水力损失,提高水轮机的效率。

2.2 转轮叶片设计及对比分析

2.1.1 叶片翼形优化

由于水轮机的出水流道部分损失较大,需通过改变出水流道进口水流的流态,减小该部分损失,而其流态与转轮出口水流相关,因此对初始叶片的出水边进行改造设计,分析转轮出口水流流态对出水流道水力损失的影响。

利用BladeGen软件对初始叶片(叶片0)的出水边与轮毂截面处翼形进行设计,选取其中5种叶片(叶片编号1、2、3、4、5)。各叶片的翼形参数表达如下:每个转轮叶片均由空间截面Span=0、0.25、0.5、0.75、1.0处的5个不同翼形拟合而成,其中Span=0为轮毂处截面,Span=1.0为轮缘处截面。选取其中Span=0、0.5、1.0进行参数表达,假设每个叶片的翼形中心线角度为γ,γ满足的方程见表1。

表1 各叶片的翼形中心线角度满足的方程

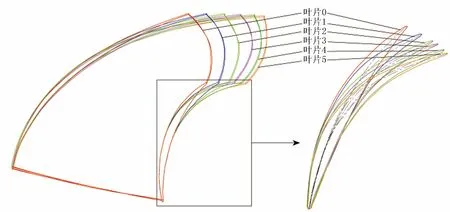
图2 转轮叶片及叶片轮毂处翼形放大示意图Fig.2 Runner blades and enlarged blade airfoils on hub

通过改变表1中翼形中心线角度曲线来调节叶片的出水边位置,在相同水头、转速和导叶开度的条件下进行数值模拟计算,以求获得损失较小的叶片模型,提高此水轮机的效率。转轮叶片及叶片轮毂截面处翼形见图2。

2.2.2 不同叶片外特性对比分析

分别将优化前的叶片(叶片0)和优化后的叶片(叶片1、2、3、4、5)在设计水头为2 m、额定转速为195 r/min下进行数值模拟计算。表2为不同叶片时水轮机的外特性参数计算结果。

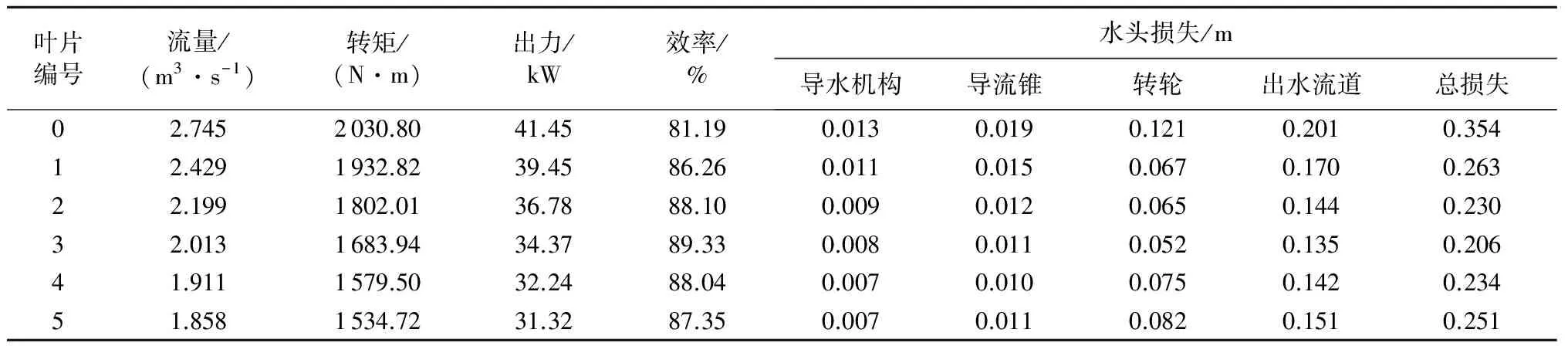
表2 不同叶片出水边形状对虹吸水轮机外特性参数的影响

由表2可以看出,通过改变转轮叶片出水边能够有效地提高虹吸式水轮机的效率,选用叶片1到叶片3时转轮和出水流道的水头损失逐渐减小,水轮机效率逐渐提高,其中叶片3的水头损失最小,水轮机效率最高。继续改变叶片出水边翼形时,即叶片4和叶片5,模型出水流道水头损失增加,效率下降,因此需要进一步分析转轮出口水流流态对出水流道水头损失的影响。

2.3 叶片出水边对出水流道损失的影响分析

虹吸式出水流道的进口边界流态对其水力性能有着不可避免的影响,而出水流道的进口边界取决于转轮出口的水流流态。一般情况下,转轮出口的水流具有一定的剩余环量,呈螺旋状进入出水流道。根据表2结果分析转轮出口水流对出水流道水力损失的影响,其流态由出口处水流的切向速度和轴向速度决定,根据涡角[14]的概念可定量表达转轮出口的水流流态,引用平均涡角[15]分析不同叶片对虹吸式出水流道水头损失的影响,平均涡角的定义为

(3)

图3 转轮出口水流平均涡角与出水流道水力损失的关系Fig.3 Relationship between average swirl angle at runner outlet and hydraulic loss in outlet conduit

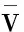
根据式(3)计算装置不同叶片时转轮出口水流的平均涡角,并将转轮出口水流平均涡角和出水流道水头损失两者的关系绘制成曲线图,见图3。

根据图3可知,装置不同叶片时的转轮出口水流对出水流道的影响也不同,为了更深入地分析这两者之间的关系,将装置不同叶片时出水流道内水流的流态进行对比。图4显示的是装置叶片0、1、2、3、4、5时虹吸式出水流道内水流的流线。

从图4可以看出,水流流经转轮时由于受到转轮旋转的影响,在进入出水流道时具有一定惯性,此时水流呈螺旋状流动,在出水流道内易形成涡流区,从而影响出水流道的水力性能,增加出水流道的水力损失(如叶片0、1)。由于出水流道内的水流在流道弯角和流道扩散段易形成脱流,转轮出口水流具有一定的涡角能对水流起到夹持作用,使水流紧贴出水流道管壁而避免脱流现象的扩大,改善了出水流道水平段部分的水流流态,反而会使水轮机效率有所提高(如叶片2、3)。但是,当转轮出口水流涡角继续增大时,水流在出水流道入口处的撞击增大,并且主轴周围的绕流严重,撞击损失和涡流损失增大[16],使其在进入水平段部分时出现较大程度的偏流,偏心涡流对管壁产生撞击,加速形成螺旋涡带,水流流态恶化,水头损失增大(如叶片4、5)。

图4 配置不同叶片时虹吸式出水流道内水流的流线Fig.4 Flow streamlines in siphon outlet conduit with different blades

上述结果表明,通过改变叶片出水边进而改变出水流道入口水流流态可以有效减小出水流道的水头损失,其中损失最小的叶片3所对应的平均涡角是13.26°。在水头和导叶开度不变的情况下,改变转轮出口水流流态以提高水轮机效率时,效率较高的叶片所形成的涡角与其他叶片相比较,更有利于出水流道内水流的平顺流动,水头损失亦较低,其值为0.135 m,在此叶片下转轮出口的水流使得出水流道内流态较好,水力性能较优,水轮机效率较高,能将其值从81.19%提高到89.33%。

2.4 叶片数量对虹吸式水轮机性能的影响分析

从2.3节可知,在不改变水头、转速、导叶开度的情况下,装置叶片3时水轮机的水头损失较小,效率较高,因此利用叶片3分析改变叶片数量对此水轮机性能的影响。为了避免不同叶片翼形对结果产生影响,直接在转轮上增加几何参数相同的叶片。表3是不同叶片数量时水轮机的外特性参数计算结果。

表3 不同叶片数量对虹吸式水轮机外特性参数的影响

将优化后的叶片数量增加至4和5时,减小了过水断面积,致使水轮机的流量和出力有所减小,转轮效率下降较多,水头损失增大,水轮机整体效率下降。但是在叶片厚度和长度不变的条件下,增加叶片数可增加转轮的强度和刚度,当此水轮机应用水头提高时可选用叶片增加的模型。

3 结 论

a. 开发了设计水头为2 m的虹吸式水轮机,采用CFD软件进行数值模拟,对转轮叶片出水边及轮毂截面处翼形进行分析比选,最终选取效率较高的叶片3,该模型在设计工况下最高效率达到89.33%。

b. 通过改变转轮叶片翼形中心线角度方程对叶片出水边翼形进行了改造对比,运用涡角的概念描述转轮出口水流的流态,绘制转轮出口水流平均涡角与出水流道水头损失的关系曲线,并分析转轮出口水流流态对出水流道水头损失的影响,其中装置叶片3时的水头损失较小(为0.135 m),所对应的平均涡角为13.26°。

c. 改造设计后的5种叶片中叶片3的过流量和出力较初始叶片有所下降,但是其转轮和出水流道的损失减小,效率较高,水轮机内水流流态良好,更有利于虹吸式水轮机的高效稳定运行。因此,当流量受限时,叶片3是最适合于此虹吸式水轮机的叶片翼形。

d. 对虹吸式水轮机的叶片数进行设计分析,结果表明,在不改变叶片几何形状和尺寸的条件下,增加叶片数会减小过流量,并且在转速和水头不变的工况下运行时效率有所下降,但是有利于增加转轮的强度和刚度。

[ 1 ] 刘敏,周大庆,吴国颖,等. 超低水头轴流式水轮机CFD优化及流动特性研究[J].水电能源科学,2016,34(1):150-153.(LIU Min, ZHOU Daqing, WU Guoying, et al. CFD optimization and study of flow characteristics of axial flow turbine with ultra-low head[J].Water Resources and Power, 2016,34(1):150-153. (in Chinese))

[ 2 ] 周大庆,陈世凡,李超. 低水头贯流式水轮机运行特性数值仿真[J].排灌机械工程学报,2013,31(10):856-861.(ZHOU Daqing, CHEN Shifan, LI Chao. Numerical simulation on running characteristics of low head pit turbine[J]. Journal of Drainage and Irrigation Machinery Engineering(JDIME), 2013,31(10):856-861. (in Chinese))

[ 3 ] 程夏蕾,赵建达. 超低水头小型水电站技术发展[J].小水电,2009(2):3-5.(CHENG Xialei, ZHAO Jianda. Small hydropower station technology development with low head[J].Small Hydro Power,2009(2):3-5.(in Chinese))

[ 4 ] 沈萍菲,周大庆,陈会向.基于CFD的微水头双向水轮机叶片比选及整机性能分析[J].水电能源科学,2014,32(11):150-154. (SHEN Pingfei, ZHOU Daqing, CHEN Huixiang. Blade comparison and selection and performance analysis of micro-head bidirectional turbine based on CFD[J]. Water Resources and Power,2014,32(11):150-154.(in Chinese))

[ 5 ] 郭中兴. 水电站尾水管经济尺寸的选择[J].水力发电,1957,4(6):26-28.(GUO Zhongxing. Choice of the economic size of the tail pipe of the hydropower station [J].Water Power, 1957,4(6):26-28.(in Chinese))

[ 6 ] 李海峰,何明辉,潘再兵.虹吸式出水流道虹吸形成过程数值模拟[J].排灌机械工程学报,2015,33(11):932-939. (LI Haifeng, HE Minghui, PAN Zaibing. Numerical simulation of siphon formation in siphon discharge passage[J]. Journal of Drainage and Irrigation Machinery Engineering(JDIME),2015,33(11): 932-939. (in Chinese))

[ 7 ] 杨帆,刘超,孙丹丹,等. 轴流泵装置虹吸式出水流道内流机理数值分析[J].农业机械学报,2015,46(6):60-65.(YANG Fan, LIU Chao, SUN Dandan, et al. Numerical investigation of internal flow mechanisms of siphon outlet passage in pumping system[J]. Transactions of the Chinese Society for Agricultural Machinery,2015,46(6):60-65.(in Chinese))

[ 8 ] 杲东彦.虹吸式出水流道三维紊流数值模拟及优化实验研究[D].江苏:扬州大学,2003:1-76.

[ 9 ] GOTTLIEB S, TONE F, WANG C, et al. Long time stability of a classical efficient scheme for two-dimensional Navier-Stokes equations[J].SIAM Journal on Numerical Analysis,2012,50(1):126-150.

[10] ZHOU Xiaoquan, CAO Shuyou, QU Lunfu, et al. Periodic boundary condition in simulation of turbulent flow[J]. Journal of Hydrodynamics (Ser B),2012,14(3):111-116.

[11] 陈国谦,杨志峰. 对流扩散方程的二阶紧凑迎风差分格式[J].水动力学研究与进展,1993,8(增刊1):499-507. (CHEN Guoquan, YANG Zhifeng. The compact second-order upwind finite difference schemes for the convection-diffusion equations[J]. Journal of Hydrodynamics, 1993,8(Sup1):499-507. (in Chinese))

[12] LIU Yangwei, LU Lipeng, FANG Le, et al. Modification of spalart-allmaras model with consideration of turbulence energy backscatter using velocity helicity[J].Physics Letters A,2012,375(24):2377-2381.

[13] 成立,刘超. 基于CFD技术的泵站进水池水力性能研究[J].河海大学学报(自然科学版), 2009,37(1):52-56. (CHEN Li, LIU Chao. Hydraulic performance of pump sumps based on CFD approach[J]. Journal of Hohai University(Natural Sciences). 2009,37(1):52-56. (in Chinese))

[14] American hydraulic institute. American national standard for pump intake design:ANSI/Ⅲ 9.8-1998[S].Washington:American National Standards Institute, 1998.

[15] 梁金栋,陆林广,徐磊,等. 轴流泵装置导叶出口水流速度环量对出水流道水力损失的影响[J].农业工程学报,2012,28(1):55-59.(LIANG Jindong, LU Linguang, XU Lei, et al. Influence of flow velocity circulation at guide vane outlet of axial-flow pump on hydraulic loss in outlet conduit[J]. Transactions of the CSAE, 2012,28(1):55-59. (in Chinese))

[16] 郑源,陈德新. 水轮机[M]. 北京:中国水利水电出版社,2011:48-50.

Influence of runner blade on hydraulic performance of siphon turbine based on CFD

YU Yunyun, QIN Zhansheng, ZHOU Daqing, LIU Min

(CollegeofEnergyandElectricalEngineering,HohaiUniversity,Nanjing210098,China)

In order to efficiently utilize the ultra-low head water resources, an axial flow turbine with a siphon outlet conduit was designed, and three-dimensional CFD numerical simulations were conducted with the design head and rated runner speed. The hydraulic loss of each flow passage component was calculated to study the hydraulic performance of the siphon turbine. The relationship between the flow regime at the runner outlet and the head loss of the outlet conduit was analyzed by changing the runner blade airfoil, and the influence of different runner blades on the hydraulic performance of the siphon turbine was studied. The results show that, with a constant water head, runner speed, and guide vane opening, the head loss in the outlet conduit of the turbine in the modified scheme with the third blade is at a minimal value of 0.135 m, the corresponding average swirl angle is 13.26o, and the turbine efficiency is at the maximum (89.33%). In addition, the influence of the number of blades on the hydraulic performance of the siphon turbine was analyzed through selection of the blade with the maximum efficiency.

siphon turbine; outlet conduit; blade; swirl angle; hydraulic loss

10.3876/j.issn.1000-1980.2017.04.003

2016-07-22

国家自然科学基金(51339005)

俞芸芸(1992—),女,江苏南京人,硕士研究生,主要从事水力机械研究。E-mail:yuyunyunhhu@163.com

周大庆,副教授。 E-mail:zhoudaqing@hhu.edu.cn

TV734.1;TK733+.3

A

1000-1980(2017)04-0298-06