基于模糊PID的山地果园运输机动力稳定系统的设计与试验

吴伟斌，张成，洪添胜*，杨晓彬，张伟，冯灼峰

(1.国家柑橘产业技术体系机械研究室，广东 广州 510642；2.南方农业机械与装备关键技术教育部重点实验室，广东 广州 510642；3.广东省山地果园机械创新工程技术研究中心，广东 广州 510642；4.华南农业大学工程学院，广东 广州 510642)

基于模糊PID的山地果园运输机动力稳定系统的设计与试验

吴伟斌1,2,3,4，张成4，洪添胜1,2,3,4*，杨晓彬4，张伟4，冯灼峰4

(1.国家柑橘产业技术体系机械研究室，广东 广州 510642；2.南方农业机械与装备关键技术教育部重点实验室，广东 广州 510642；3.广东省山地果园机械创新工程技术研究中心，广东 广州 510642；4.华南农业大学工程学院，广东 广州 510642)

以提高华南农业大学研制的山地果园轻简化轮式运输机作业动力控制稳定性为目标，设计加装了一种成本较低的动力稳定系统。系统由制动手柄、电推杆、电磁阀、制动油泵、制动钳组成。根据控制策略在Simulink中建立动力独立控制模型，经过仿真分析，在稳态之后非受控的动力轮速度与受控动力轮的速度相等，整车驱动力增大，提高了运输机在路况参数多变路面的通过性，并在动力稳定系统的基础上加入了自适应模糊PID速度控制器，对其进行了仿真分析。结果表明, 在3.5 s时，两侧动力轮纵向速度之差进入稳定响应，稳态绝对误差绝对值最大值为0.422 2，最小值为0.004 7，响应到达并保持在终值±5%误差内所需的最短时间为3.0 s，稳态条件下(t→∞)的误差为 0，加快了系统响应速度，提高了调节精度与稳定性。对运输机实车测试，受控后稳态车轮速度的绝对误差为0.178 1～0.396 1 km/h，相对误差为0.71%～5.27%，与仿真结果一致。

山地果园运输机；Matlab；动力稳定控制；模糊PID；仿真

山地果园运输机主要用于生产过程的运输[1]，对降低劳动强度与生产成本，提升运输效率具有重要意义。山地果园大多路况复杂，路面不平整，附着系数与坡度不均一[2-3]，对果园运输机加装多功能的动力控制系统虽能提高安全系数，但令运输成本增加，因而有必要研制低成本的动力控制系统，以提高作业的安全系数与运输效率。

DOUMIATI等[4]利用监测车辆轮速、制动、转向、车速，分析车辆行驶轨迹偏差与驱动力分配状况，建立闭环监控系统对车辆进行驱动力分配控制，在干、湿路面上进行车辆偏航试验，降低翻车几率。颜娟娟等[5]在 Matlab/Simulink中建立了“魔术公式”轮胎模型和8自由度整车动力学模型，针对ESP系统的非线性时变特性，设计了基于横摆角速度和质心侧偏角的联合模糊控制器, 提出了附加横摆力矩的转矩主动分配策略,并在易于失稳的湿滑路面上进行了典型工况的仿真。赵方庚等[6]通过各类传感器监测各车轮转速、转向角度、制动位置与发动机节气门开度，制定车辆差速器锁止机构自动控制系统(vehicle differential lock system，VDLS)的控制策略，提高越野车在复杂路况下的通过性，解决动力轮陷坑、转向侧向不稳定、附着力低等问题，但专用于农用运输机动力控制技术的研究鲜有报道。笔者针对现有果园运输机的动力稳定性较差，而加装市面上多功能动力控制装置将增加运输成本的问题，为华南农业大学研制的山地果园轻简化轮式运输机设计加装了一种低成本的动力稳定系统，根据控制策略在Simulink中建立动力独立控制模型，在动力稳定系统的基础上加入了模糊PID速度控制器控制速度，以提高运输机的动力稳定性。

1 山地轮式运输机的结构参数

华南农业大学研制的轻简化轮式运输机主要由发动机总成、变速器、减速器、差速器和车轮组成，如图1所示。运输机最大爬坡角度为15°，最小转弯半径为2.74 m，空载质量为330 kg，平地最大装载质量能达到250 kg，最高车速为13.5 km/h，整车尺寸为1 690 mm×1 170 mm×300 mm，前轮轮距为870 mm，后轮轮距为955 mm，车轮半径为300 mm。

图1 山地果园轻简化轮式运输机的结构Fig.1 Structure of simple wheeled transporter in hill orchard

2 运输机动力稳定系统总体设计

运输机的后桥采用没有限滑装置的圆锥齿轮式差速器，若运输机一侧动力轮陷入泥坑，则另一侧动力轮所受行驶阻力将加大，差速器将分配更多的扭矩到陷入坑中的动力轮，造成行驶通过性下降。该运输机原动力系统中的两侧动力轮由一个制动手柄压缩制动油泵进行制动，使两侧制动钳在制动液的压力加大情况下，同时压紧两侧制动盘，使两侧动力轮同时制动。

如图2所示，动力稳定系统由制动手柄、电推杆、电磁阀、制动油泵、制动钳组成。在其原动力系统上，每侧制动控制增加了电推杆控制制动油泵，利用电磁阀实现制动手柄与电推杆的控制分离，检测数据由单片机分析、处理后，再对电磁阀与电推杆实施控制。

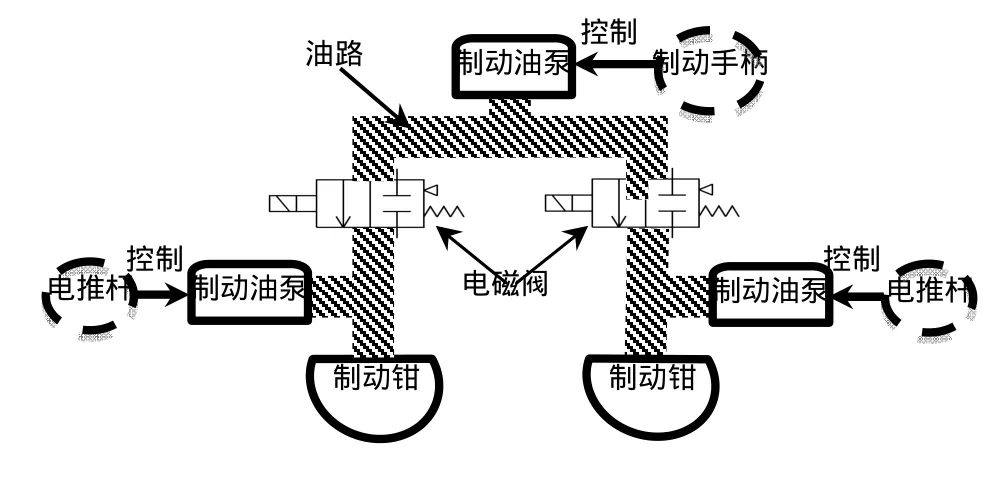
图2 动力稳定系统的组成Fig.2 Composition of dynamic stabilization system

动力稳定系统先通过轮速传感器与转向角度传感器采集运输机行驶工况参数，并由微控制器分析数据，计算动力轮滑移率，判断运输机动力轮滑移率是否超过极限滑移率，即是否处于陷入泥坑状态，若判断结果为是，则对陷入泥坑的动力轮提供相应阻力，即施加独立制动力，令其滑移率达到目标值，而阻力由丝杆步进电机控制制动器的制动油泵产生，丝杆步进电机受微控制器控制。

3 运输机动力系统模型的建立

根据研究目标，构建自由度数适中的7自由度运输机动力系统模型和Magic Formula轮胎模型。7自由度模型，包括了运输机纵向、侧向、横摆运动以及4个车轮的回转运动的7个自由度[7-9]。模型中，忽略运输机的垂直方向运动以及运输机的俯仰及侧倾运动，并假设左右车轮转向角一致，各轮胎的特性相同。

3.1 运输机整车运动模型方程

1) 对纵向方向运动，有

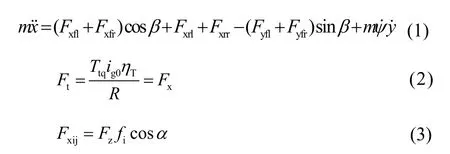
2) 对横向方向运动，有

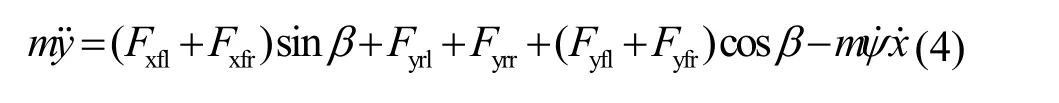
3) 对横摆运动，有

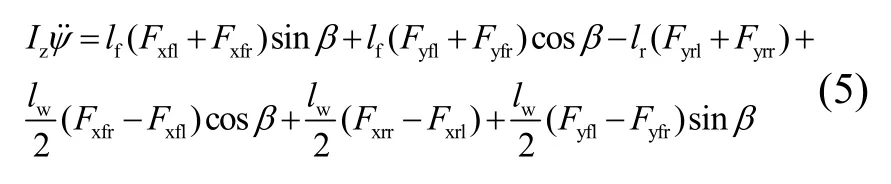
式中：Iz为橫摆转动惯量；lf为质心到前车轴的距离；lr为质心到后车轴的距离；lw为左右两侧车轮的距离。

车轮动力学模型

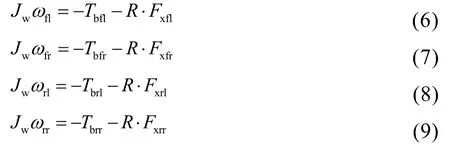
式中：Jw为车轮转动惯量；Tbij为各车轮的制动力矩；uxij为车轮中心沿轮胎运动平面的纵向速度；ωij为车轮绕其中心轴的回旋角速度。

依据文献[10]，各个车轮中心沿轮胎运动平面的纵向速度与功率的关系为

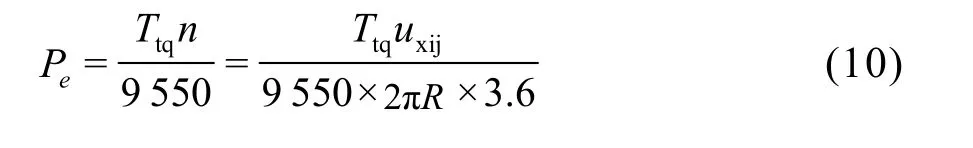
4 运输机动力稳定系统仿真模型构建与分析

4.1 仿真工况参数设置

仿真中运输机的相关参数设置：整车满载质量m为510 kg，车轮滚动半径R为 0.3 m，固定功率Pe为10 kW，单个动力轮的垂直载荷Fz为1 400 N，单个从动轮的垂直载荷Fzf为1 150 N。

仿真中路面附着系数的设置：在干燥的土路附着系数为 0.5～0.6，湿土路面为 0.2～0.4[10]，假定左侧与右侧的路面附着系数分别为0.1与0.7，则假运输机左动力轮陷入泥泞土坑中，泥泞土路的车轮滚动阻力系数为 0.10～0.25，泥泞土路湿度越高，车轮滚动阻力系数越大[11-12]，因此仿真中左侧与右侧的车轮滚动阻力系数分别为0.25与0.10。

4.2 运输机动力系统仿真模型的建立与分析

对运输机的发动机到车轮的动力传动进行建模，以运输机两侧路面附着系数为自变量，在发动机提供额定功率以及差速器作用下计算出实际车速与目标车速，最后以滑移率作为因变量输出结果，观察滑移率的变化。

1) 车轮纵向驱动力的计算。运输机在仿真中被假定为只沿直线运动，根据公式(11)，同时在Simulink中建立模型。

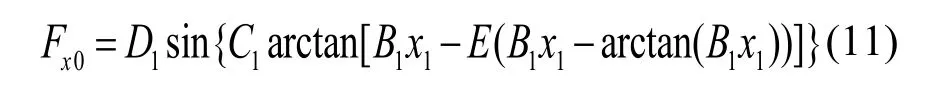
式中：x1为纵向滑移率，即x1=λ；B1为刚度因子，；C1为曲线形状因子，纵向力计算，即令；D1为峰值因子，表示曲线的最大值，即为纵向力零点处的纵向刚度，即E1为曲率因子，表示曲线最大值附近曲线形状，即

2) 车轮行驶阻力的计算。直线行驶中，从动轮与地面的摩擦力以及各车轮的滚动阻力构成了运输机的行驶阻力∑fF(行驶坡度约等于 0，忽略空气阻力)[12-14]。利用公式(12)计算可得出行驶阻力，其中2个从动轮的摩擦阻力相等，车轮滚动阻力系数相等。在Simulink中建立相应的计算模型。

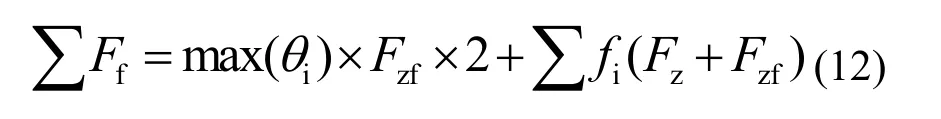
3) 滑移率计算模块。滑移率是在车轮运动中滑动成分所占的比例，取值范围为0～100%，计算公式(13)如下，同时在Simulink中建立模型。

4) 运输机动力系统仿真结果。图 3-a为 10 s内滑移率的变化，由于左侧路面附着系数小于右侧路面附着系数，使得左侧动力轮在额定功率下转速高于右侧动力轮，所以左侧滑移率大于右侧滑移率，当滑移率高于0.14时，运输机车轮的地面附着力将相应地下降。

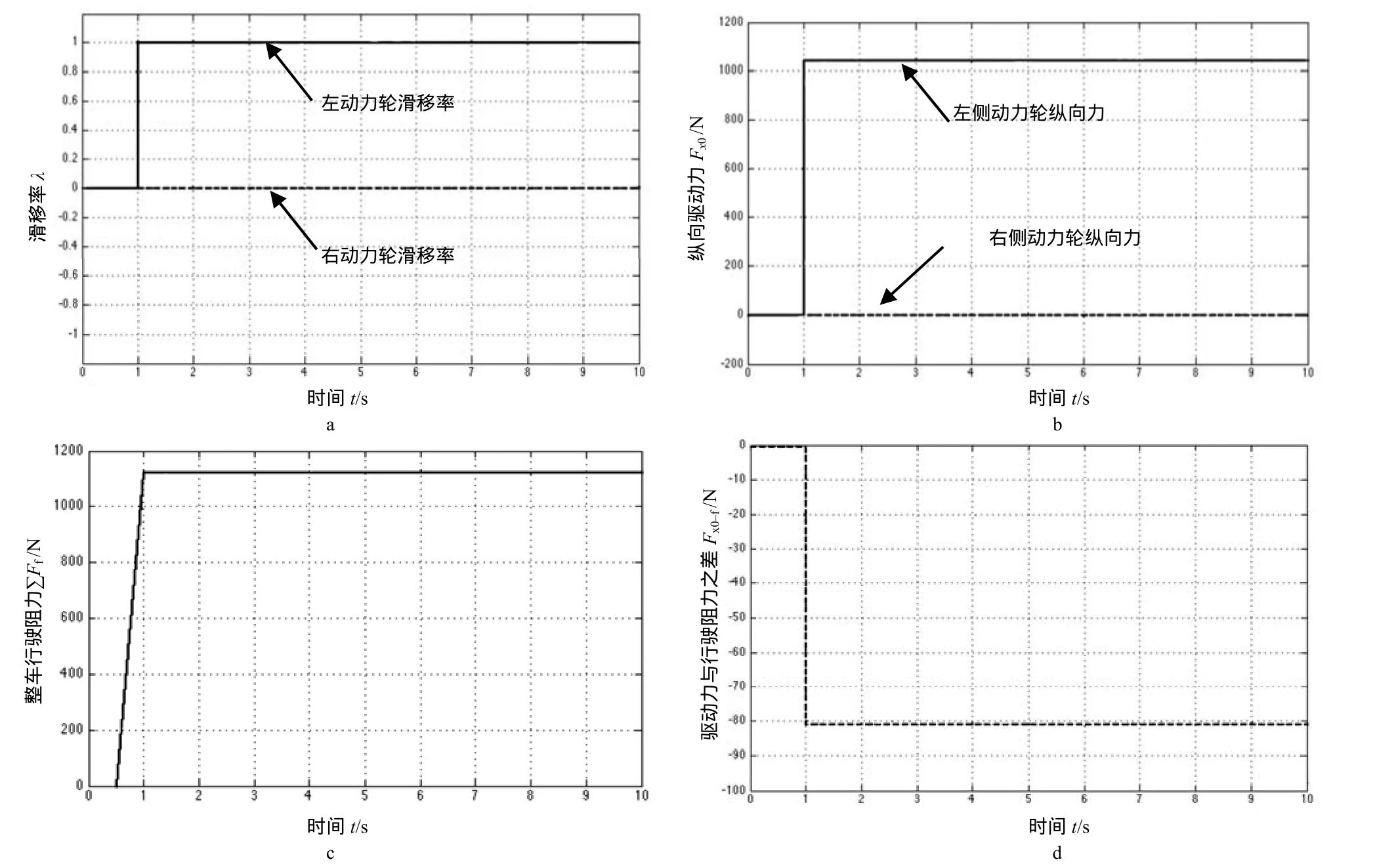
图3 山地果园轮式运输机动力系统仿真结果Fig.3 Simulation results of dynamic system of wheeled transporter in hill orchard

图3-b为左侧与右侧动力轮纵向力的仿真结果，从图中可以看出, 左侧动力轮纵向驱动力Fx0l远大于右侧动力轮纵向驱动力Fx0r，且右侧动力轮纵向力为0，则右侧动力轮没有受到前进的推力。

图3-c为运输机整车行驶阻力仿真结果。

从以上仿真结果得出，在假定运输机左侧动力轮陷入泥泞土坑时，由于差速器的作用，在发动机功率固定的条件下，右侧动力轮速度为 0、滑移率为0、驱动力为0，左侧动力轮速度大于0、滑移率为100%、驱动力大于0。尽管车轮总驱动力大于0，但由从动轮引起的摩擦阻力与各车轮的滚动阻力组成的车体行驶阻力大于车轮总驱动力，使得左侧动力轮空转于泥泞土坑中，而车体速度为 0，运输机稳定性与通过性降低，无法按照驾驶员意愿直线前进。

4.3 运输机动力稳定系统仿真模型的建立与分析

在运输机动力系统基础上，加入制动扭矩，以控制动力轮纵向方向的速度，建立运输机动力稳定系统仿真模型。对失稳的动力轮加以控制，以保证运输机行驶的稳定性与通过性，对失稳的动力轮控制主要体现在控制动力轮的滑移率达到目标值。

1) 动力稳定控制模块。设定目标滑移率=14%，极限滑移率=20%。在运输机动力系统的仿真结果中，若令大于20%的滑移率降至14%，需要向滑移率大于20%的动力轮施加制动力Fbki。所施加的制动力Fbki等于非陷坑动力轮摩擦阻力与陷坑动力轮摩擦阻力的差值，可由公式(14)计算得到，式中假定动力轮处于陷坑状态。在Simulink中建立的仿真模型如图4所示，系统中独立施加的制动力由电推杆控制油泵产生液压力挤压制动钳与制动盘而产生，每0.5 s能产生100 N的制动力。

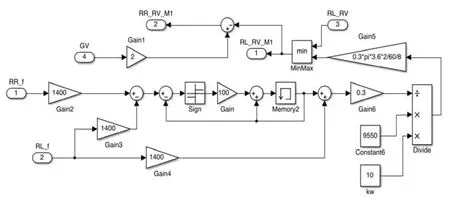
图4 受控动力轮速度制动模型Fig.4 Speed brake model of managed power wheel

2) 车体纵向速度计算模块。利用所建立的驱动力模型与行驶阻力模型，得出ΣFX0与ΣFf，导入公式(15)，可得到车体纵向瞬时速度uTt。将uTt作为理论车速带入滑移率的计算模块中，得出2动力轮的滑移率，再由轮胎模型重新计算，形成闭环系统仿真。同时在Simulink中建立仿真模型。

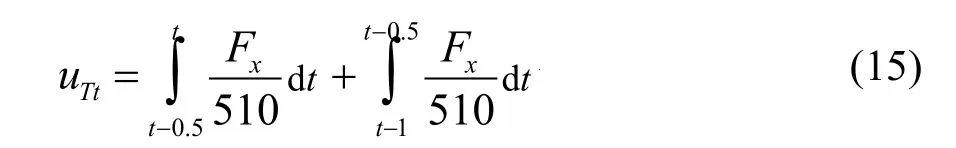
3) 运输机动力稳定系统仿真结果。当系统检测出动力轮滑移率高于20%时，便对该动力轮持续施加制动力，令2动力轮纵向速度趋于相等，如图5-a所示。图5-b为左侧与右侧动力轮受动力稳定模块控制后，仿真所得的滑移率变化情况。计算滑移率的目标车速由车体纵向速度来决定，在2.5 s前右侧动力轮的滑移率为0。从1 s开始，左侧动力轮受到系统对其施加的制动力，在差速器的作用下，右侧动力轮车轮纵向速度逐渐增大，当2动力轮速度相等时，系统的制动力不再增加并维持在固定值。2动力轮的滑移率在4.5 s后趋于相等，在5.5 s后两侧动力轮的滑移率逐渐趋于 0。另外，在图中可以看出，电推杆控制从响应到车轮速度达到稳态所需时间约为3.5 s。

如图5-c所示，在动力稳定模块控制下，2.5 s后车体纵向驱动力逐渐上升，在各车轮的路面附着系数与行驶阻力系数不变的条件下，两侧动力轮纵向速度与车体纵向速度逐渐趋于相等，在5.5 s后接近相等，同时车体纵向驱动力大小在一定范围内往复变化，从而维持速度不变，达到运输机按驾驶者意愿直线行驶的控制目标。

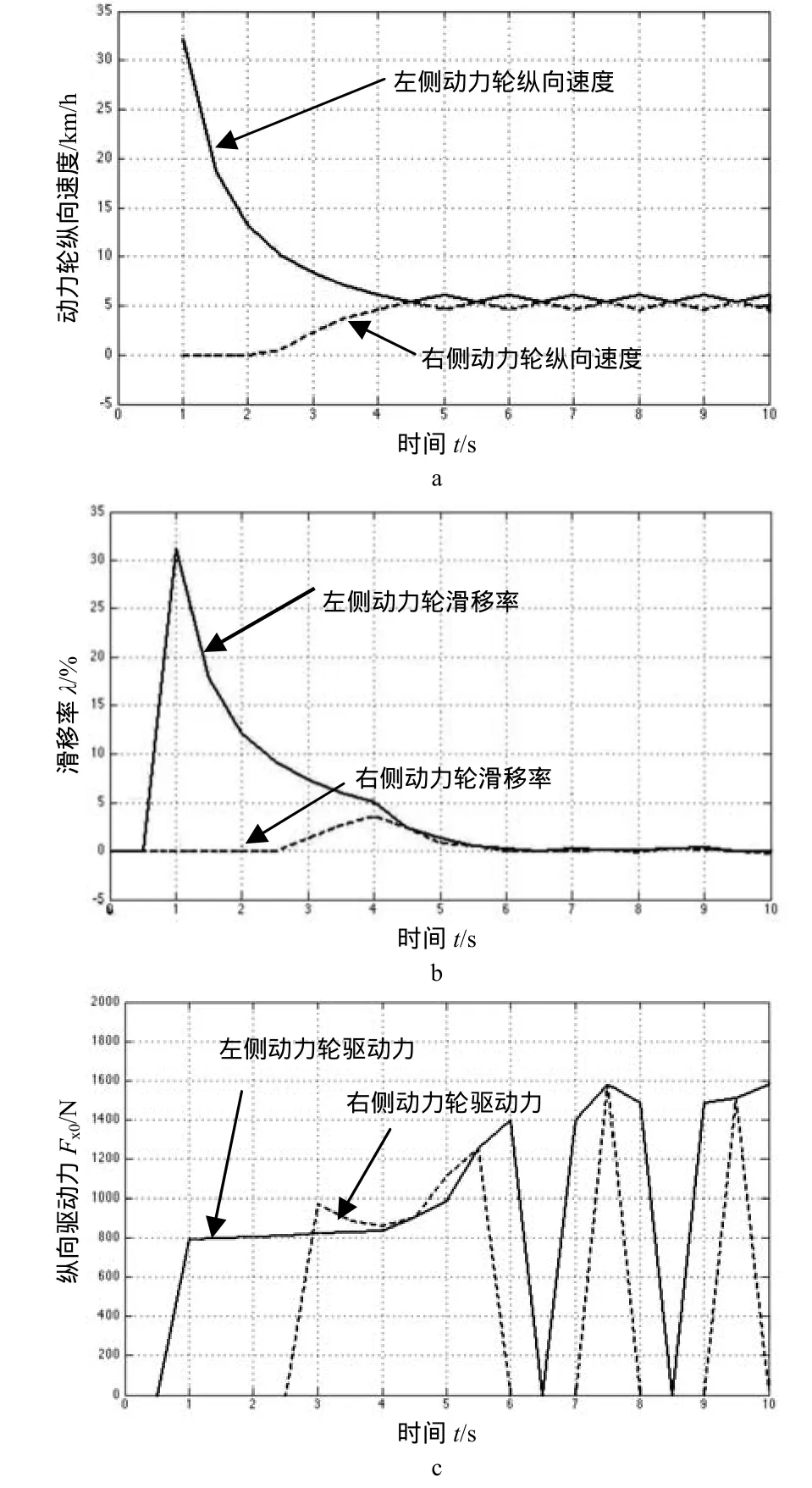
图5 山地果园轮式运输机动力稳定系统仿真结果Fig.5 Simulation results of dy namic stabilization of w heeled transporter in hill orchard

4.4 模糊PID速度控制器的应用

在动力稳定模块施加制动力至受控动力轮，在使其纵向速度与另一侧动力轮的纵向速度达到相等的过程中，电推杆压缩制动泵对受控动力轮施加制动力，由于电推杆均匀压缩制动泵产生非线性油压，因此施加的制动力呈非线性增大，加之制动盘和制动钳表面摩擦系数不均、制动过程中温度上升等因素的变化都可能改变制动力，使受控动力轮速度不稳。这些因素共同作用使得动力稳定控制过程相当复杂。从控制理论上讲，动力稳定控制的工作过程具有明显的非线性、时变性和不确定性[12-15]，因此，很难建立精确的数学模型。为解决此问题，在该动力稳定系统中加入模糊PID速度控制器模块。

利用试凑法[16-19]对PID参数进行整定，整定过程中，比例系数kp以超调量最大为选取标准，选取kp0=1.5；积分作用系数ki以稳态时间最短为选取标准，选取ki0=0.1；微分作用系数kd以稳态时间最短与稳态误差最小为选取标准，选取kd0=0.015。依据模糊PID控制器的控制规律以及经典PID的控制方法[20-21]，将模糊控制与传统PID控制相结合的模糊自适应PID，使得系统具有模糊控制的灵活性和适应性强，又有PID精度高的优点。将输入的误差(e)和误差微分(ec)分为7个模糊集：NB(负大)，NM(负中)，NS(负小)，ZO(零)，PS(正小)，PM(正中)，PB(正大)，即模糊子集为 e，ec={NB，NM，NS，ZO，PS，PM，PB}。将输出的 Δkp、Δki、Δkd也分为 7个模糊集：NB(负大)，NM(负中)，NS(负小)，ZO(零)，PS(正小)，PM(正中)，PB(正大)，即模糊子集为 Δkp，Δki，Δkd=｛NB，NM，NS，ZO，PS，PM，PB｝。根据控制要求，确定误差e、误差微分ec及控制量Δkp、Δki、Δkd的模糊集和论域，对模糊变量选定隶属函数，建立模糊规则。

在Simulink中建立的模糊PID控制器仿真模型如图6所示。

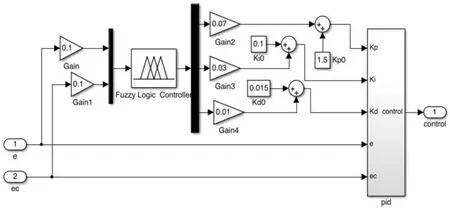
图6 模糊PID控制器仿真模型Fig.6 Fuzzy PID controller of simulation model

将模糊PID速度控制器模块加入到所建立的动力稳定系统模块中进行仿真，结果如图7所示。结合Matlab/Worksapce中的仿真数据，在3.5 s时，两侧动力轮纵向速度之差进入稳定响应，稳态绝对误差绝对值最大值为0.422 2，最小值为0.004 7。对比图5-a中的仿真结果，表明响应到达并保持在终值±5%误差内所需的最短时间为3.0 s，稳态条件下(t→∞)的误差为 0，模糊 PID控制器令系统的响应速度加快。

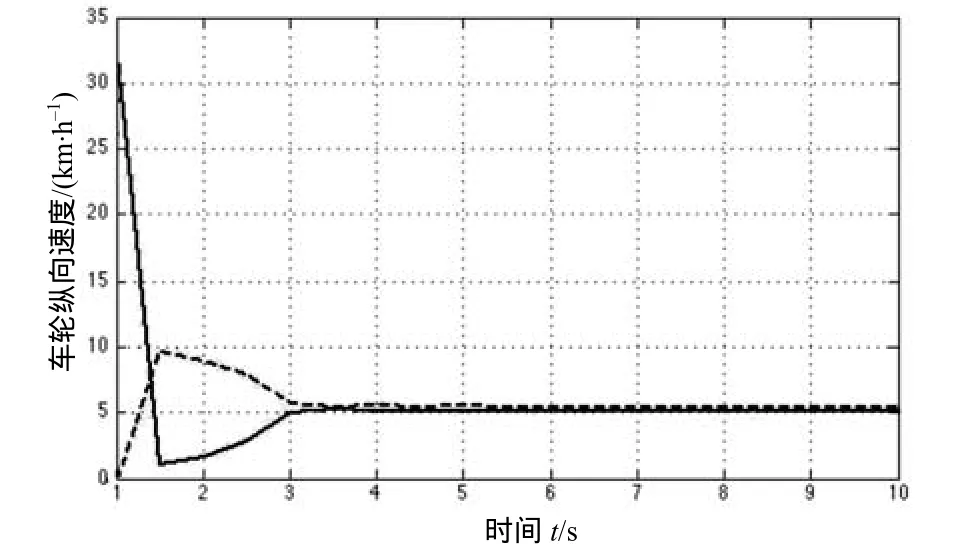
图7 基于模糊PID控制器的两侧动力轮速度变化仿真结果Fig 7 Simulation results of the speed variation of the dynamic wheel on both sides controlled by fuzzy PID controller

5 验证试验

为了验证动力稳定系统的效果，进行了运输机实车试验。

试验采用Arduino公司的Mega2560单片机进行数据采集与I / O输出控制，通过USB接口与笔记本电脑连接，采用Arduino IDE软件中的Serial Monitor采集数据并记录。试验前对发动机节气门开度、车轮转向角度、制动油泵活塞行程进行标定，将山地果园轮式运输机动力轮悬架于试验台架的滚轮上进行试验。

以2个动力轮速度中的最小值为目标速度，控制非陷坑的动力轮达到目标速度，陷坑的动力轮出坑后系统不再加以控制，2动力轮速度达到相等值为最终控制目标，验证系统可行性。试验中节气门开度为怠速至40%之间，转向角度为0°，车轮速度稳定后开始对车轮速度进行控制。受控后车轮速度误差列于表 1，按照控制策略，以两侧动力轮中速度最小的作为系统控制下速度的标定值，另一侧为测量值。

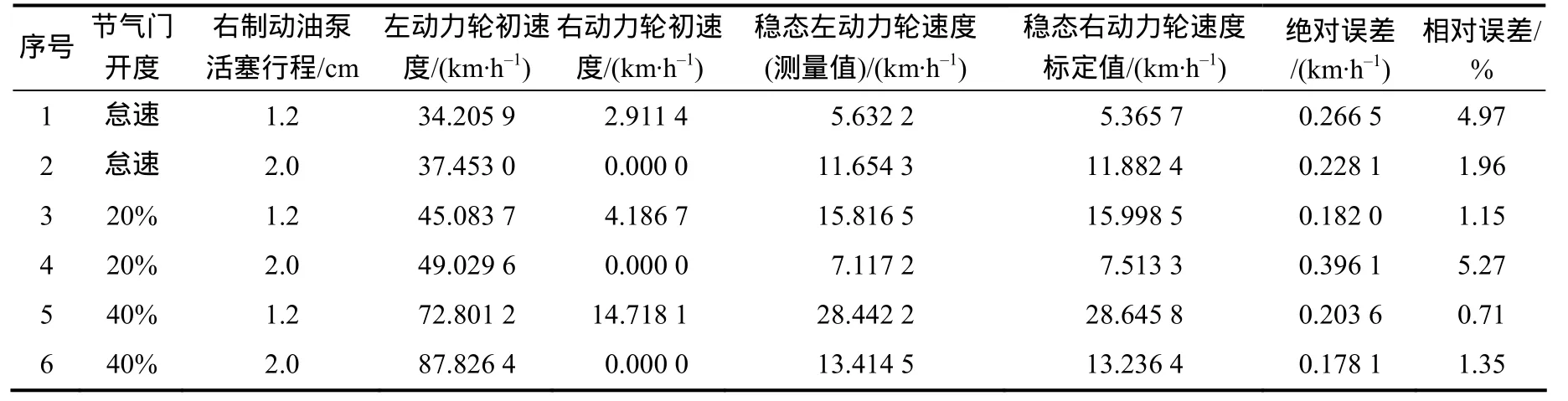
表1 车轮速度误差分析结果Table 1 Error analysis of wheel speed

试验结果表明：所设计的控制系统能有效地降低陷坑后两侧动力轮之间的速度差，并使两侧动力轮的速度逐渐趋于相等。电推杆控制制动泵产生独立制动力来使两侧动力轮所受到的行驶阻力相等，控制时间只需1～2 s。受控后稳态车轮速度的绝对误差为 0.178 1～0.396 1 km/h，相对误差范围为0.71%～5.27%，试验结果与仿真结果一致。

6 结论

本研究以华南农业大学研制的轻简化轮式运输机为研究对象，对其原有的动力控制系统进行了改进设计，在 7自由度模型和轮胎模型的基础上，推导出车辆纵向方向上的动力学模型，以滑移率控制为目标，设计运输机动力独立控制的控制策略，并在Simulink建模，进行了仿真分析。从仿真结果可以看出，华南农业大学研制的山地果园轻简化轮式运输机动力控制系统效果较差，在运输机动力轮遇到特殊情况如陷入泥泞土坑时，稳定性与通过性降低，运输机无法正常行驶，而在改进设计后的动力稳定控制系统中，由于每侧制动控制增加了电推杆控制制动油泵，对动力轮进行制动二次控制，运输机的稳定性与通过性大大增强；在动力稳定系统中加入模糊PID速度控制器后，两侧动力轮纵向速度之差进入稳定响应所需时间提高14.3%，从而提高了系统响应速度与稳定性。实车试验结果表明，所设计的控制系统能有效地降低陷坑后两侧动力轮之间的速度差，并使两侧动力轮的速度逐渐趋于相等，控制时间仅需 1～2 s。受控后稳态车轮速度的绝对误差范围为0.178 1～0.396 1 km/h，相对误差范围为0.71%～5.27%，试验结果与仿真结果一致。

由于模型的仿真采用Matlab/Simulink软件，在仿真过程中设定的路面属性参数单一，不能对运输机在不同路面同时进行综合分析，因此，为提升仿真结果的精确性，可考虑用Adams软件建立路谱，将路面属性的仿真参数输入到Matlab/Simulnk中，再对动力独立控制系统进行仿真，从而使仿真结果更加全面可靠。

[1] 洪添胜，张衍林，宋淑然，等．山地果园运输与喷雾机械的研究与应用[J]．现代农业装备，2014(5)：21-27．

[2] 洪添胜，张衍林，杨洲，等．果园机械与设施[M]．北京：中国农业出版社，2012：143-147．

[3] 吴伟斌，赵奔，朱余清，等．丘陵山地果园运输机的研究进展[J]．华中农业大学学报，2013，32(4)：135-142．

[4] DOUMIATI M，SENAME O，DUGARD L，et al.Integrated vehicle dynamics control via coordination of active front steering and rear braking[J]．European Journal of Control，2013，19(2)：121-143．

[5] 颜娟娟，夏长高．汽车ESP系统控制策略的仿真研究[J]．汽车工程，2014，36(8)：989-993．

[6] 赵方庚，姜丁，朱先民，等．越野汽车差速锁止机构自动控制系统控制策略研究[J]．汽车工程，2005，27(1)：97-99．

[7] 马晓．不同轮胎模型对重型载货汽车整车性能仿真的影响分析[D]．长春：吉林大学，2013．

[8] 王娟，李同杰，孟令启，等．基于七自由度整车模型的汽车振动特性分析[J]．安徽科技学院学报，2013，27(1)：72-76．

[9] 时培成，王立涛，高洪，等．基于四轮独立制动及整车模型的 VSC系统仿真[J]．农业机械学报，2007，38(6)：14-19．

[10] 余志生．汽车理论[M]．3版．北京：机械工业出版社，2009．

[11] 李亮，贾钢，宋健，等．汽车动力学稳定性控制研究进展[J]．机械工程学报，2013，49(24)：95-107．

[12] 张丽霞，孙杨，潘福全，等．汽车ESP系统联合控制仿真研究[J]．农业装备与车辆工程，2013，51(8)：39-42．

[13] 杨世勇，徐国林．模糊控制与PID控制的对比及其复合控制[J]．自动化技术与应用，2011，30(11)：8-11．

[14] 靳立强，宋传学，王云成．基于主动安全的轮间电控限滑差速器控制方法研究[J]．汽车工程，2015，27(3)：347-349．

[15] CHOUINARD A，LÉCUYER J F．A study of the effectiveness of electronic stability control in Canada[J].Accident Analysis & Prevention，2011，43(1)：451-460．

[16] 王述彦，师宇，冯忠绪．基于模糊 PID 控制器的控制方法研究[J]．机械科学与技术，2011，30(1)：167-171．

[17] 张丽霞，孙杨，潘福全，等．基于模糊自适应 PID 的汽车驾驶机器人的车速控制[J]．汽车工程，2012，34(6)：512-516．

[18] 谢文云．电控限滑差速器限滑转矩与整车性能匹配的仿真研究[D]．长春：吉林大学，2012．

[19] 叶阳，刘昭度，裴晓飞，等．基于联合控制的汽车驱动防滑系统[J]．沈阳工业大学学报，2012，33(6)：672-677．

[20] TOIMIL D，GÓMEZ A，ANDRÉS S M．Data-driven ESP modelling and optimisation[J]．Journal of Aerosol Science，2014，70：59-66．

[21] CHU L，GAO X，GUO J，et al．Coordinated control of electronic stability program and active front steering[J].Procedia Environmental Sciences，2012，12：1379-1386．

[22] 韩伟．基于限滑差速器的汽车性能仿真与试验研究[D]．长春：吉林大学，2013．

责任编辑：罗慧敏

英文编辑：吴志立

Design and experimental of dynamic stability system for mountain orchard transporter based on the self-tuning fuzzy PID controller

WU Weibin1,2,3,4, ZHANG Cheng4, HONG Tiansheng1,2,3,4*, YANG Xiaobin4, ZHANG Wei4, FENG Zhuofeng4
(1.Division of Citrus Machinery, China Agriculture Research System, Guangzhou 510642,China; 2. Key Laboratory of Key Technology on Agricultural Machine and Equipment, Ministry of Education, Guangzhou 510642, China;3.Guangdong E & T Research Center for Mountainous Orchard Machinery, Guangzhou 510642, China; 4.College of Engineering, South China Agricultural University, Guangzhou 510642, China)

To improve the control stability of mountain orchard transporter designed by South China Agricultural University, a power stabilization system with low cost was designed and installed. The system consists mainly of brake handle, electric push rod, electromagnetic valve, brake oil pump, and brake clamp etc. According to the control strategy,power independently control model is established in Simulink. Through the simulation analysis, the speed of uncontrolled power wheel equals the speed of controlled power wheel and vehicle driving force increases under steady state, to improve passing ability of the transporter under the changeable road condition. Furthermore, the adaptive fuzzy PID speed controller is joined to the system. The simulation results show that the stable response was started at 3.5 s for the difference between the longitudinal velocity of momentum wheel on both sides with the maximum absolute error of 0.422 2 and the minimum value of 0.004 7. Response to reach and maintain the final value error of plus or minus 5%within the shortest time of 3.0 s. Under the condition of the steady state (t→∞), the error is 0, increasing the systemresponse speed and improving the accuracy and stability. The results of test in vehicle showed that the absolute error of controlled post-steady wheel speed range of 0.178 1-0.396 1 km/h and the relative error range of 0.71%-5.27%, which was consistent with the simulation results.

mountain orchard wheeled transporter; Matlab; dynamic stability control; PID; simulation

S237；TP274.2

A

1007-1032(2017)04-0443-08

2016-12-29

2017-03-10

公益性行业(农业)科研专项(201203016，201403036)；现代农业产业技术体系建设专项(CARS-27)；“十二·五”农村领域国家科技计划课题(2014BAD16B0103)；广东省科技计划项目(2014A070713032)

吴伟斌(1978—)，男，广东中山人，博士，教授，主要从事农业工程、机电一体化和信息技术应用研究，wuweibin@scau.edu.cn；*通信作者，洪添胜，博士，教授，主要从事农业工程、机电一体化和信息技术应用研究，tshong@scau.edu.cn