基于桥系数的分裂社区检测算法研究

2017-07-18冀庆斌李德玉王素格

中文信息学报 2017年3期

关键词：复杂度系数强度

冀庆斌，康茜，李德玉，王素格

(山西大学计算机与信息技术学院, 山西太原 030051)

基于桥系数的分裂社区检测算法研究

冀庆斌，康茜，李德玉，王素格

(山西大学计算机与信息技术学院, 山西太原 030051)

研究社区结构有助于揭示网络结构和功能之间的关系，而社区检测是社区结构研究的基础和核心。该文定义了一种聚集度桥系数，将其应用到社区检测中，设计出一种分裂社区检测方法，包括分裂和合并两个算法。分裂算法使用桥系数识别社区间边，通过迭代删除社区间边分解网络，从而发现网络中的社区结构；合并算法根据社区连接强度合并社区，可以揭示社区结构中的分层嵌套的现象。在六个社会网络数据集上的实验表明，本文算法可以有效的将网络分裂为有意义的社区，并且准确性接近或超过经典的社区检测算法。

社区检测；分裂算法；桥系数

1 引言

现实世界中的许多系统，如朋友网、协作网和Internet等都可以抽象成复杂网络[1]，这些网络都具有社区结构的特征，即网络中的节点可以自然形成节点组，同一个节点组内的节点的连接具有稠密性，而不同节点组间的节点的连接具有稀疏性[2]。研究社区结构有助于分析网络的特性[3]，而社区检测是社区结构研究的基础和核心[4]，通过网络拓扑信息，识别网络中连接稠密的节点组[5]用于社区的发现。

为了获得复杂网络中的社区结构，学者们从不同的角度提出了许多社区检测方法，主要有：相似度方法[6]、模块度方法[7]、谱方法[8]、派系过滤方法[9]、块模型方法[10]、标签传播方法[11]和分裂方法[12]等。其中，分裂方法是较早开始研究的一类社区检测方法，其核心问题是社区间边的识别。通过迭代删除社区间边，分裂方法用于分解网络，从而获得网络中的社区结构。

GN算法[13]使用边介数识别社区间边，是一种典型的分裂方法，其计算边介数的时间复杂度为O(mn)[14]，而整个算法的时间复杂度为O(n3)。为了提高边介数的计算效率，Tyler等[15]采用抽样的方法降低边介数的计算复杂度，Green等[16]使用并行技术提高边介数的计算效率。然而抽样需要网络的统计信息，难以普遍推广，而并行计算仅提高了计算速度，时间复杂度问题没有得到很好的解决。文献[17]利用节点相似度将无权网络映射为加权网络，通过边的权重识别社区间边，但映射过程需要邻接矩阵的乘法运算，使得整个算法的时间复杂度大于O(n3)。

Radicchi等[18]认为使用局部指标识别社区间边可降低分裂算法的时间复杂度。目前，这类局部指标主要有边聚类系数[18]和最大团桥系数[19]，但当边聚类系数的阶数较大时就不再是局部指标[5]。文献[20]利用文献[19]的桥系数，认为桥系数大的边更可能是社区间边，提出了一个凝聚算法。最大团桥系数直接用于分裂社区检测有两点不足：(1)求解最大团算法的时间复杂度大于O(n2)[21]，因此直接引入最大团桥系数不能降低分裂算法的时间复杂度；(2)文献[19]提出最大团桥系数的目的是加速网络分解，而网络分解与社区检测的要求并不相同[22]。本文从网络中节点局部聚集的角度，定义了基于局部聚集度的桥系数，以有效识别社区间边，进而以桥系数为基础设计了社区检测算法，用于降低分裂算法的时间复杂度，提高分裂算法的效率。

BGLL算法[23]使用模块度作为度量，采用逐步合并的方法合并社区，从而得到了社区的层次关系。但是已有研究[24,25]发现，模块度方法存在分辨率限制，使用模块度评价社区划分质量不一定能够得到真实的社区结构[2,26]，为此Chertkov等人[27]使用p-强社区来评价社区的质量。本文借鉴BGLL算法[23]和p-强社区[27]的思想，设计了社区合并算法，可以揭示社区的层次结构。

2 聚集度桥系数和社区强度的定义

2.1 最大团桥系数

为了量化网络中边的连接强度，Cheng等[19]提出了最大团桥系数的概念，定义如下：

其中，x和y是边e的两个端点，Sx、Sy和Se分别是包含节点x、y和边e的最大团的规模。

网络中的团可以刻画节点的局部聚集特性[28]，因而最大团桥系数本质上是一种对节点局部聚集度的度量。

2.2 聚集度桥系数

在网络分析中，一般使用聚类系数度量节点的局部聚集程度[29]；同时文献[30]指出，偏好依赖是现实网络的一大特点，因此节点的度也是度量节点聚集程度的重要指标。由此，给出本文聚集度桥系数的定义。

给定无向网络G=(V, E)，V={x}表示网络中n个节点的集合，E={(x, y)}表示网络中m条边的集合。对于节点x，记N(x)为其近邻，N[x]={x}∪N(x)为其闭合近邻[31]，GV′为节点集V′对G的导出子图。对于子网络G′和其中的一个节点x，x在G′中的聚类系数记为Cx|G′，x在G′中的度记为dx|G′。

定义1对于边(x,y)，聚集度桥系数定义为

其中，N[x]-{y}表示删除边(x, y)后节点x的闭合近邻。

式(2)可以表示如下的意义：如果一条边的两个端点的共同邻居较少，而且删除边后各自聚集邻居的程度较强，则这条边连接其端点的能力就较弱。

由于分子上的阶数并不改变其单调性，因此，式(2)可以改写为式(3)。

2.3 社区强度

为了评价社区的质量，Chertkov等人[27]提出了p-强社区的概念，要求社区满足以下条件：

将公式(4)改写，给出社区强度的形式化定义。

定义2社区强度定义为

可知，社区强度表示内部度大于外部度的节点数在整个社区中所占的比例。对于式(5)，有p∈[0～1]，p越大，表示社区越强；当p=1时，社区成为强社区。

社区合并的过程中，应该首先合并连接最紧密的社区。为此，本文使用社区连接强度来度量社区连接的紧密程度。

定义3两个社区的连接强度定义为

其中，Sc1表示社区c1内部边的数量，ωc1,c2表示社区c1和c2之间边的数量。T越大，表示两个社区之间的连接越强，越有可能合并为一个社区。

3 基于桥系数的分裂社区检测算法

为了检测出网络中的社区结构，本节给出基于桥系数的分裂社区检测方法(bridgeness index algorithm，BI算法)。首先使用桥系数将网络分解为多个小社区，然后根据社区连接强度合并小社区。BI算法包括分裂网络、合并社区两个算法。

3.1 使用桥系数分裂网络算法

基本思想：利用桥系数作为移除边的标准，不断重复删除桥系数最大的边，直到桥系数均为零或社区划分的模块度不再增加为止。

算法1Splitting(G)，使用桥系数分裂网络算法。

输入：网络G (V, E)。

输出：初始社区划分P。

Begin

(1) 初始化模块度Q=0，社区数C=1；

(2) 计算所有的桥系数bi；

(3) while(True)

(4) 找出最大桥系数bix,y；

(5) 如果 bix,y=0，跳到步骤(11)；

(6) 删除边(x,y)；

(7) 重新计算CC和Q；

(8) 如果CC增大而Q不再增大，跳到步骤(11)；

(9) 更新节点x和y的邻接边的桥系数；

(10) end；

(11) 返回社区划分P。

End

利用算法1，可将桥系数最大的边识别为社区间边。在计算一条边的桥系数时，需要遍历两个端点的邻居和二步邻居[32]一次即可，由此可以看出，聚集度桥系数是一个典型的局部指数。

3.2 使用社区连接强度合并社区算法

基本思想：根据社区连接强度逐层合并社区，直到合并后的社区强度不再增加为止。

算法2Merging (G, P)，使用社区连接强度合并网络算法。

输入：网络G (V, E)，初始划分P。

输出：包含层次关系的社区划分Pc。

Begin

(1) 初始化, 计算P包含的社区数CC；

(2) while(True)

(3) 计算所有社区间的连接强度Tc1,c2；

(4) 找出连接强度最大的两个社区i和j；

(5) 计算合并前的社区强度pi和pj，以及合并后的社区强度p；

(6) 如果 p < sqrt(pi, pi)，跳到步骤(9)；

(7) 合并社区i和j，并更新P和T；

(8) end；

(9) 返回包含层次关系的社区划分Pc。

End

算法2的合并过程可以看成是社区间逐渐吸引的过程，用于发现重叠的社区结构。当整个网络作为一个社区时，社区连接强度不再有意义，由此算法2至少可以得到两个社区。

3.3 BI算法时间复杂度分析

在BI算法中，计算最耗时的部分是算法1中对桥系数的计算。

(1) 计算整个网络的桥系数的复杂度：计算一条边的桥系数需要计算两个点聚类系数和一条边聚类系数，而计算一个节点和一条边的聚类系数的复杂度均为O(k2)，因此，计算整个网络的桥系数的复杂度为O(3mk2)。

(2) 迭代过程的复杂度：当删除一条边后，需要更新两个端点的邻接边的桥系数，而更新过程的复杂度为O(2k·3k2)。在最差情况下，需要删除m条边，整个迭代过程的复杂度为O(2mk·3k2)。

综上所述，整个算法的时间复杂度为O(3mk2+2mk·3k2)，即在稀疏网络中的时间复杂度近似于O(nk3)。

4 实验结果及分析

本节将在六个真实的社会网络数据集上测试BI算法的有效性。同时，与其他几个具有代表性的社区发现算法GN算法[13]、CNM算法[7]、BGLL算法[13]和LPA算法[11]进行比较。

4.1 实验数据集

本文使用的六个社会网络数据集如下。

(1) Zachary’s Karate Club (简称Karate)，是二十世纪七十年代一所美国大学的空手道俱乐部的34名成员间的朋友网[33]，真实网络拥有两个社区。

(2) Dolphin Social Network (简称Dolphins)，是生活在新西兰Doubtful Sound海湾的一群62只海豚间的接触网[34]，真实网络拥有两个社区。

(3) Books about US Politics(简称PolBooks)，是亚马逊网上书店售卖的关于2004年美国总统选举的政治图书间的关系网，真实网络拥有三个社区。

(4) American College Football(简称Football)，是根据2000年美国高校美式足球秋季常规赛季的分组比赛情况形成的网络，真实网络拥有12个社区。

(5) Jazz Musicians Network (简称Jazz)，是根据1912～1940年之间的198个爵士乐乐队之间的合作关系形成的网络。Gleiser等[35]最早研究了这个网络，指出Jazz网络大致包括两个社区。

(6) General Relativity and Quantum Cosmology Network[36](简称GR-QC)，是电子预印本文库中1993年1月至2003年4月之间关于广义相对论和量子宇宙论范畴论文作者之间的科学合作网。

这六个数据集的基本统计性质如表1所示。

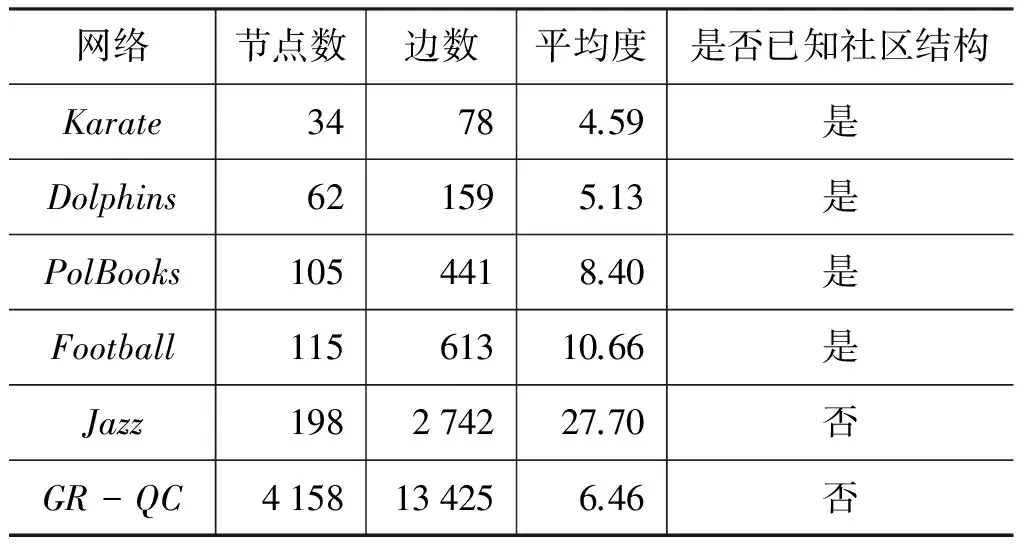
表1 本文使用数据集的基本统计性质

4.2 评价指标

本文使用以下三个指标评价社区划分的质量：

(1) FVIC(fraction of vertices identified correctly)，正确划分的节点总数占所有节点数的比率。对于已知社区结构的网络，给出社区划分后，即可计算有多少比例节点的划分是正确的。

(2) 归一化互信息(NMI)[37]。算法发现的社区个数与真实社区个数并一定相等，这种情况下可以使用基于信息论的NMI对划分结果进行评价。NMI定义为

其中，N为混淆矩阵；Ni,j表示“真实”社区i和发现的社区j重合的节点个数；Ni.为矩阵第i行的元素之和；N.i为矩阵第j列的元素之和；CR表示“真实”社区的个数；CF表示发现的社区个数；R表示“真实”社区；F表示发现的社区。

(3) 模块度[2,7]。它是一个衡量社区划分质量的客观的指标。对于未知社区结构的两个网络，可以使用模块度检测算法结果的有效性。

4.3 实验结果及分析

实验1使用BI算法检测Karate网络中的社区结构

在Karate网络上运行BI算法，其中算法1将Karate网络划分为四个社区，分别用三角形、菱形、正方形、圆形代表；算法2根据社区连接强度将四个社区合并为两个社区，结果如图1所示，两个社区以虚线分隔。真实的社区结构如图2所示。

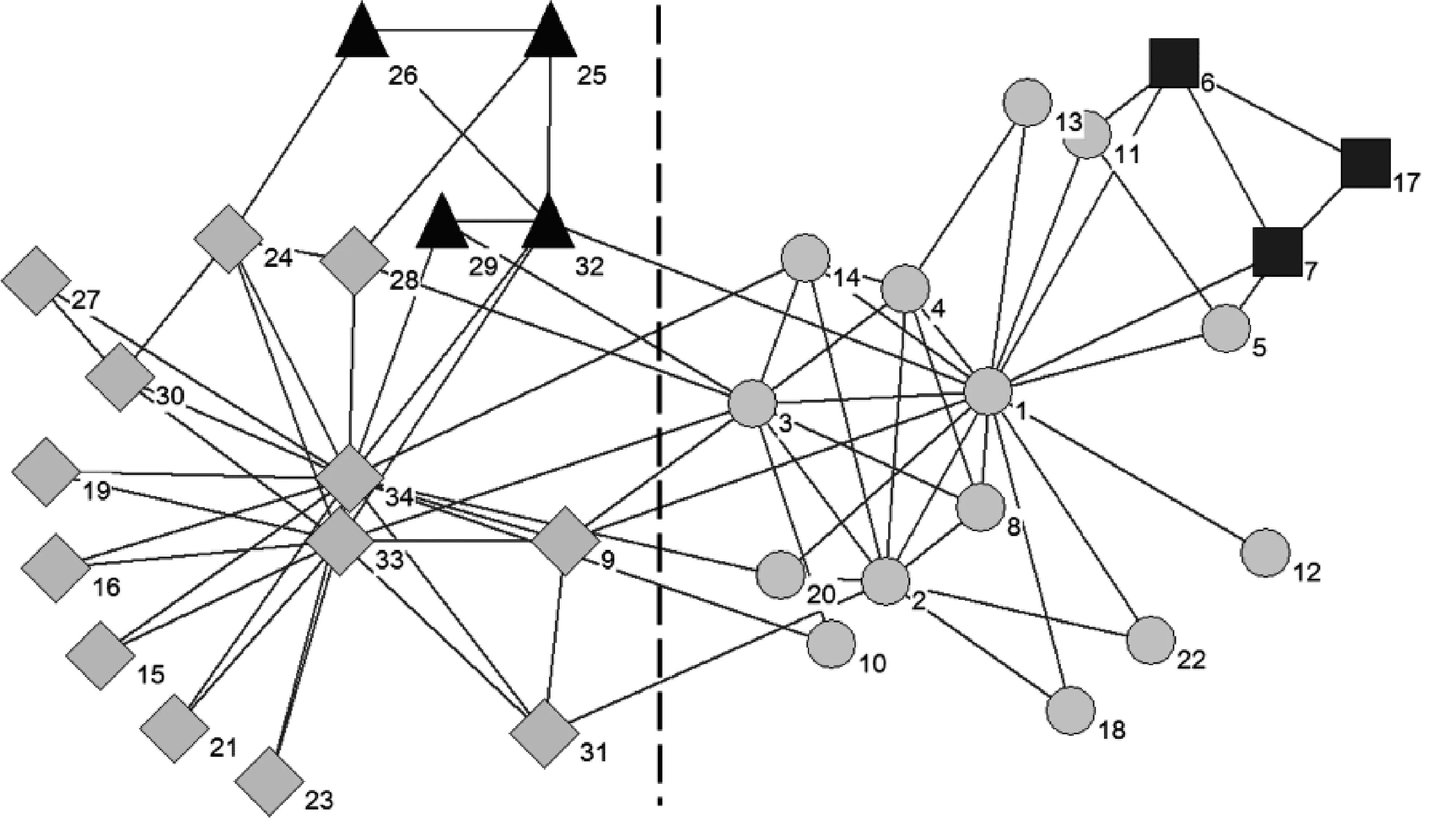
图1 BI算法在Karate网络上发现的社区结构

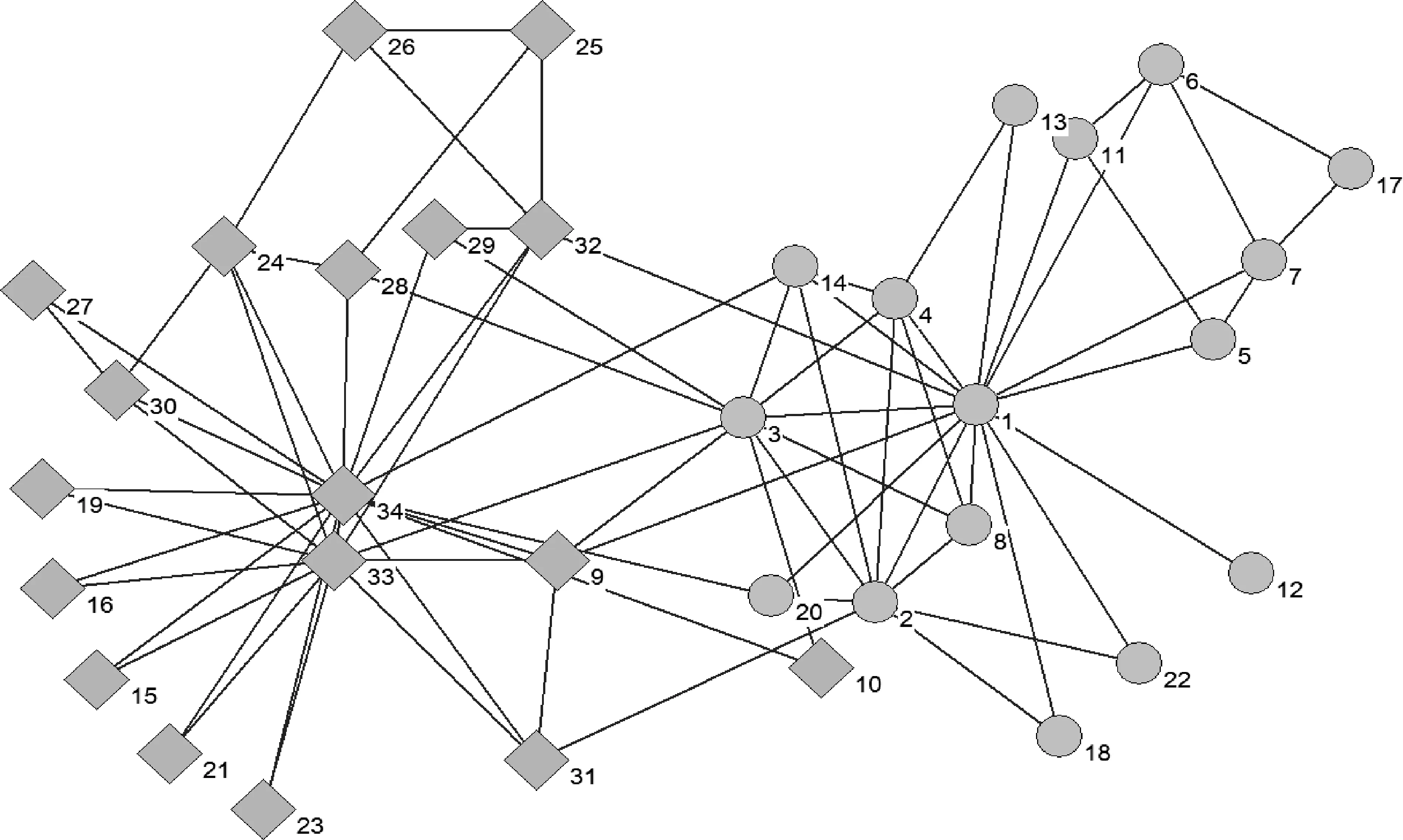
图2 Karate网络上真实的社区结构

由图1和图2可以看出，BI算法得到的社区结构与真实的社区结构几乎一致，除了一个节点10被错误划分。事实上，节点10与两个社区联系的紧密程度差不多。因此，BI算法可以发现Karate网络中真实的社区结构，并能检测到网络中的重叠社区。

实验2使用BI算法检测Dolphins网络中的社区结构

在Dolphins网络上运行BI算法。算法1在Dolphins网络中发现了六个小社区(分别使用不同颜色和形状代表)，并且得到了最大的模块度值Q=0.433 7；算法2根据社区间的连接强度将六个社区合并为两个社区，如图3所示，两个社区之间以虚线分隔。真实的社区结构如图4所示。

图3 BI算法在Dolphins网络得到的社区结构

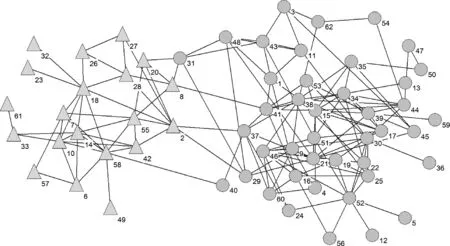
图4 Dolphins网络上真实的社区结构

由图3和图4可以看出，BI算法的结果与真实的社区结构几乎一致，仅有一个节点31划分错误。这说明BI算法能够有效的发现Dolphins网中的社区结构。

实验3比较BI算法和GN算法对PolBooks网络的划分结果

本实验在PolBooks网络上同时运行BI算法和GN算法，实验结果如表2所示。

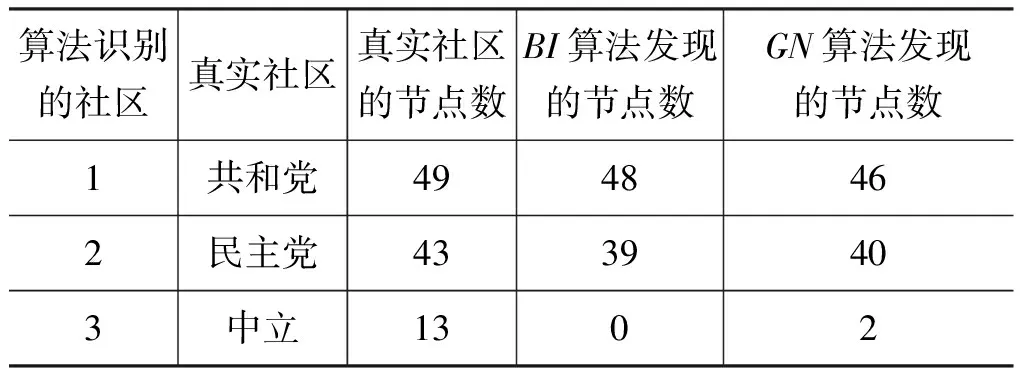
表2 BI算法和GN算法对于PolBooks网络的划分结果分析

由表2可以看出，虽然BI算法仅得到两个社区，但基本分开了“共和党”和“民主党”两个社区，正确率为82.86%，略低于GN算法的83.81%；虽然GN算法可以识别出“中立”社区，但正确率只有15.38%。这个结果是可以接受的，有以下原因：由于美国两党之间的政治主张明显对立，中立政客在所有议题上也不可能都中立，因此仅使用拓扑结构很难识别出“中立”社区。这说明，BI算法能够在PolBooks网络上以很高的准确率发现真实的社区结构。

实验4在四个已知社区结构网络上，比较BI算法与其他算法的社区划分质量

本实验将测试BI算法与其他四个常用算法的社区划分质量。为了客观的比较不同算法，实验在四个已知社区结构网络上进行，使用FVIC和NMI指标比较社区划分的准确性。同时，实验做了以下设定：(1) 限定了GN、CNM算法得到的社区数；(2) 由于BGLL算法不能限定社区数，因此不比较BGLL算法的FVIC值；(3) LPA算法得到的结果很不稳定，取五次结果的平均值。实验结果见表3。

从表3可以看出，在四个网络中BI算法都能够以接近最高的准确度检测出真实的社区结构，算法的准确性接近或超过其他算法，表明了BI算法能够有效的发现真实的社区结构。

实验5测试BI算法分裂网络的有效性

本实验将在Jazz和GR-QC两个未知社区结构的网络上运行算法1，检验算法1是否可以有效的分裂网络。模块度可以客观的评价社区划分质量，因此通过考查网络分裂过程中模块度的变化趋势，可以评价算法能否有效的分裂网络。实验结果如图5、图6所示。

表3 BI算法与其他常用算法在已知社区结构网络上的比较

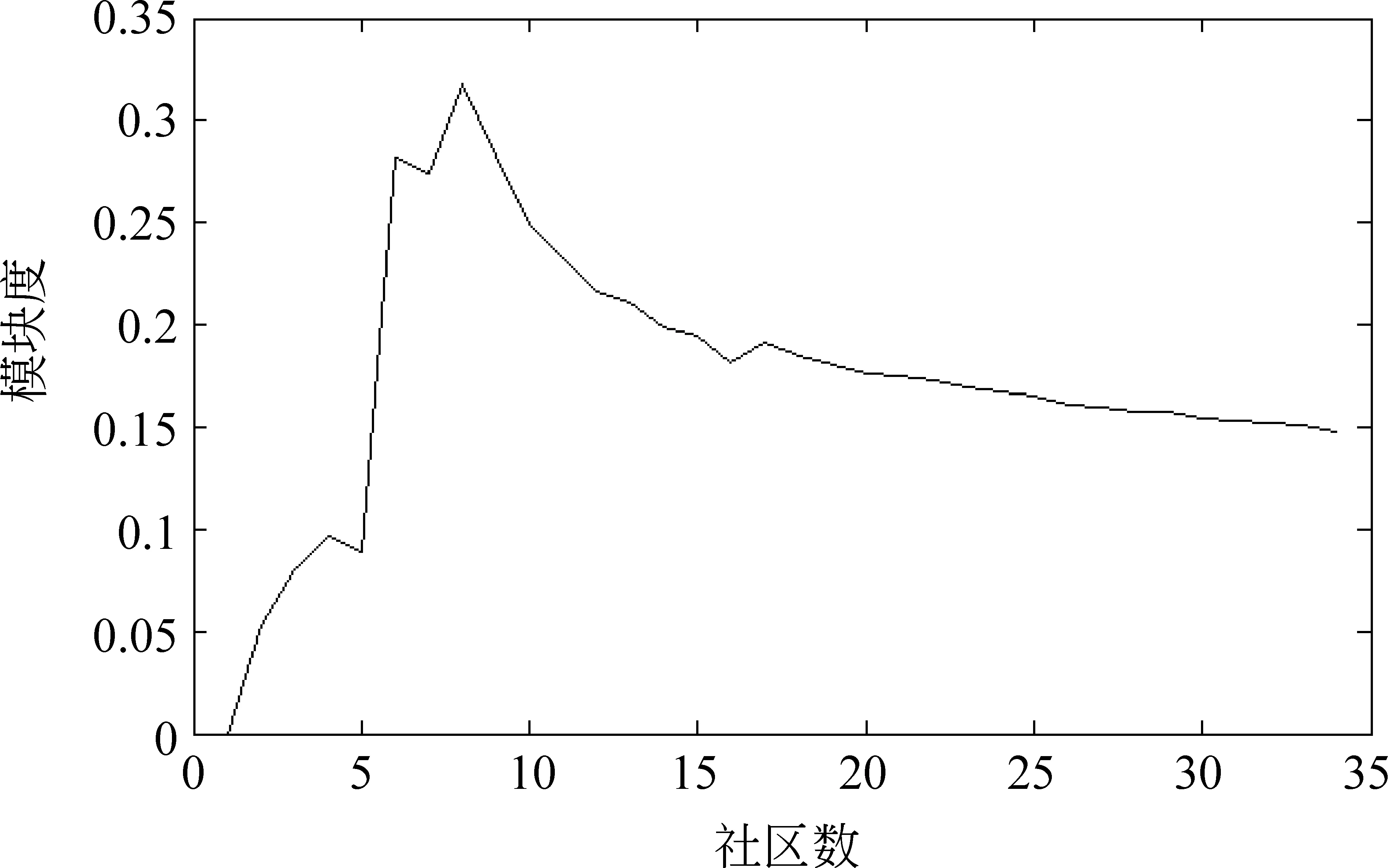
图5 BI算法在分裂Jazz网络时模块度的变化

图6 BI算法在分裂GR-QC网络时模块度的变化

从图5、图6可以看出，随着网络的分解，社区划分的模块度逐渐增加，从而得到局部最大值。这与GN算法、CNM算法中模块度的变化趋势一致。这个实验说明，BI算法分裂网络的方向是正确的，算法可以将网络分裂为有意义的社区。

实验6比较BI算法和BGLL算法对Jazz网络的划分结果

本实验将在未知社区结构的Jazz网络上同时运行BI算法和BGLL算法。BI算法在Jazz网络上得到两个社区，模块度为0.289，与最早研究Jazz网络的文献的研究结果一致。BGLL算法在Jazz网络上得到四个社区，模块度为0.445；在BGLL算法的结果上运行算法2，能够得到两个社区。结果如图7、图8所示。

从图7、图8可以看出，尽管BGLL算法可以得到更大的模块度和更多的社区，但图8中的三角形、正方形和圆形代表的三个社区连接比较紧密，通过算法2可以合并为一个社区。执行算法2后，BI和BGLL算法的划分结果仅有两个节点不同。这说明，BI算法与BGLL算法的结果具有一定的相似性，但BI算法的结果能够更好的反映真实的社区结构。

图7 BI算法在Jazz网络上的结果

图8 BGLL算法在Jazz网络上的结果

实验7检测BI算法能够是否能够克服分辨率限制

本实验将在未知社区结构的GR-QC网络运行BI算法和BGLL算法，并从BGLL算法的社区划分中选择最大的一个社区，来检测BI算法是否能够克服BGLL算法的分辨率限制。取BGLL算法在GR-QC网络上发现的最大社区，以不同的颜色代表BI算法在其中检测到的社区，结果如图9所示。

从图9中可以看到，对于箭头所指的3个节点组①②③来说，内部连接非常紧密，而与外界仅有一条或两条边相连，因此可以认为这三个节点组是社区。BI算法能够识别这些规模很小的社区，而BGLL算法不能识别这些小社区。这说明，BI算法能够在大网络上识别出小的社区，在社区分辨率上优于基于模块度优化的方法。

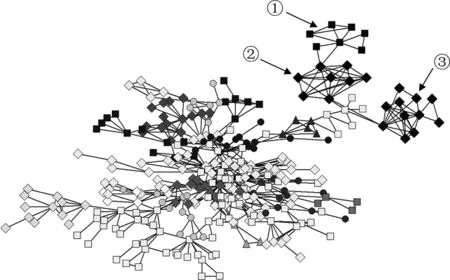
图9 BGLL算法在GR-QC网络上发现的最大社区，但BI算法能够在其中发现更小的社区

5 结束语

为了降低分裂社区发现算法的计算复杂度，本文定义了一种基于聚集度的桥系数，能够量化网络中边的连接强度。在此基础上，提出了“分裂—合并”两步实现的BI算法，计算的时间复杂度为O(nk3)，优于已有的社区分裂算法。在六个真实社会网络上的实验表明，BI算法可有效的识别真实网络中的社区结构。

随着网络的规模不断增大，往往只能得到网络的部分结构，而桥系数是局部指数，可以在部分网络中发现有意义的社区结构。同时，现实中的网络结构是不断变化的，节点之间联系会中断或产生，节点也会产生或消失，桥系数也可用于这类动态网络的社区检测。

[1] Strogatz S H. Exploring complex networks[J]. Nature, 2001, (410): 268-276.

[2] Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69(2): 026113.

[3] Cheng X Q, Shen H W. Uncovering the community structure associated with the diffusion dynamics on networks[J]. Journal of Statistical Mechanics Theory & Experiment, 2010, 33(2):147-167.

[4] 程学旗, 沈华伟. 复杂网络的社区结构[J]. 复杂系统与复杂性科学, 2011, 08(1):57-70.

[5] Fortunato S. Community detection in graphs[J]. Physics Reports, 2010, 486(3-5):75-174.

[6] 闵亮，邵良棚，赵永刚. 基于节点相似度的社团检测[J]. 计算机工程与应用，2015，51(9),77-81.

[7] Clauset A, Newman M E J, Moore C. Finding community structure in very large networks[J]. Physical Review E, 2004, 70(6)： 264-277.

[8] Nascimento M C V. Community detection in networks via a spectral heuristic based on the clustering coefficient[J]. Discrete Applied Mathematics, 2014, 176(3):89-99.

[9] Palla G, Derényi I, Farkas I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, (435): 814-818.

[10] Karrer B, Newman M E J. Stochastic block models and community structure in networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2011, 83(1 Pt 2):211-222.

[11] Nandini R Usha, Réka A, Soundar K. Near linear time algorithm to detect community structures in large-scale networks[J]. Physical Review E, 2007, 76(3):036106.

[12] Sun P G, Yang Y. Methods to find community based on edge centrality[J]. Physical A Statistical Mechanics & Its Applications, 2013, 392(9):1977-1988.

[13] Girvan M, Newman M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences, 2002, (12): 7821-7826.

[14] Sun P G, Yang Y. Methods to find community based on edge centrality[J]. Physical A Statistical Mechanics & Its Applications, 2013, 392(9):1977-1988.

[15] Tyler J R, Wilkinson D M, Huberman B A. Email as spectroscopy: Automated discovery of community structure within organizations[J]. The Information Society, 2003, 21(2): 143-153.

[16] Green O, Bader D A. Faster betweenness centrality based on data structure experimentation[J]. Procedia Computer Science, 2013, 18(1):399-408.

[17] Li L, Li S H, Li H J, et al. A community divisive algorithm based on local weak edges[J]. Journal of Information & Computational Science, 2014, 11(11):3727-3737.

[18] Radicchi F, Castellano C, Cecconi F, et al. Defining and identifying communities in networks[J]. Proceedings of the National Academy of Sciences, 2004, (101): 2658-2663.

[19] Cheng X Q, Ren F X, Shen H W, et al. Bridgeness: a local index on edge significance in maintaining global connectivity[J]. Journal of Statistical Mechanics: Theory and Experiment, 2010, 2010(10): P10011.

[20] 王玙, 高琳. 动态网络桥系数增量聚类算法[J]. 西安电子科技大学学报(自然科学版), 2013, 40(1): 30-35.

[21] 胡新, 王丽珍, 何瓦特,等. 度数法求解最大团问题[J]. Journal of Frontiers of Computer Science & Technology, 2013, 7(3):262-271.

[22] Ding Z, Zhang X, Sun D, et al. Overlapping community detection based on network decomposition[J]. Scientific Reports, 2016, (6)：24115.

[23] Blondel V D, Guillaume J L, Lambiotte R, et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics Theory and Experiment. 2008, 30(2): 155-168.

[24] Fortunato S, Barthélemy M. Resolution limit in community detection[J]. Proceedings of the National Academy of Sciences, 2007, 104(1): 36-41.

[25] Lancichinetti A, Fortunato S. Limits of modularity maximization in community detection[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2011, 84(84):2184-2188.

[26] 沈华伟, 程学旗, 陈海强, 等. 基于信息瓶颈的社区发现[J]. 计算机学报, 2008, 31(4): 677-686.

[27] Chertkov M，Chernyak V Y， Teodorescu R. Evaluating local community methods in networks[J]. Journal of Statistical Mechanics: Theory and Experiment, 2008, 49(5): P05001.

[28] Cheng X, Ren F, Zhou S, et al. Triangular clustering in document networks[J]. New Journal of Physics, 2009, 11(3):033019.

[29] Watts D J, Strogatz S H. Collective dynamics of “small-world” networks[J]. Nature, 1998, 393:440-442.

[30] Amaral L A N, Scala A, Barthélémy M, et al. Classes of small-world networks[J]. Proceedings of the National Academy of Sciences, 2000, (97): 11149-11152.

[31] Kulli V R, Warad N S. On the total closed neighbourhood graph of a graph[J]. Journal of Discrete Mathematical Sciences & Cryptography, 2001, 4(2):109-114.

[32] Newman M E J. Networks: an introduction[M]. OUP Oxford, 2010.

[33] Zachary W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research. 1977, (33): 452-473.

[34] Lusseau D, Schneider K, Boisseau O J, et al. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations: Can geographic isolation explain this unique trait[J]. Behavioral Ecology and Sociobiology. 2003, 54(4): 396-405.

[35] Gleiser P M, Danon L. Community structure in jazz[J]. Advances in Complex Systems, 2003, 6(4):565-573.

[36] Leskovec J, Lang K J, Dasgupta A, et al. Community structure in large networks: natural cluster sizes and the absence of large well-defined clusters[J]. Internet Mathematics, 2009, 6(1):29-123.

[37] L Danon, A Díaz-Guilera , J Duch , et al. Comparing community structure identification[J]. Journal of Statistical Mechanics: Theory and Experiment, 2005, 2005(09):09008.

ACommunityDetectionAlgorithmBasedonBridgeness

JI Qingbin, KANG Qian, LI Deyu, WANG Suge

(School of Computer & Information Technology, Shanxi University, Taiyuan, Shanxi 030051, China)

Study of community structure is of help to reveal the relationship between network structure and function, and community detection is essential to the community structure research. A bridgeness index based on clustering degree is defined in this paper, and applied to the community detection. The proposed algorithm includes two parts splitting and merging. The splitting algorithm identifies inter-community by bridgeness, and decomposes network by iterative removing inter-community edges until the community structure is discovered; The merging algorithm merges communities according to the community connection strength, so that the hierarchical nesting in community is revealed. Experiments on six social networks show that the proposed algorithm can effectively detect interesting communities for the whole network, and the accuracy is close to or even better than the classical algorithms.

community detection; divisive algorithm; bridgeness index