基于形态优化滤波和最小二乘支持向量机的轴承故障分析

饶 杰，张绍旺，徐光荣，张 勇

（云南省计量测试技术研究院，云南 昆明 650228）

基于形态优化滤波和最小二乘支持向量机的轴承故障分析

饶 杰，张绍旺，徐光荣，张 勇

（云南省计量测试技术研究院，云南 昆明 650228）

为实现滚动轴承故障分析，提出基于形态优化滤波和最小二乘支持向量机的轴承故障分析方法。首先，通过判别指标最大化原则确定最佳形态滤波算子；然后，用最佳形态滤波算子对滚动轴承实例故障信号进行降噪分析；最后，利用粒子群对模型参数进行寻优，利用最小二乘支持向量机建立轴承故障分析模型，并对模型效果进行评价。实验结果表明：该方法从模型稳定性、预测准确度、模型复杂度3个方面考虑，故障分析结果较优，能够更好地提取轴承故障特征信息。

滚动轴承；特征提取；形态滤波；最小二乘支持向量机；故障诊断

0 引 言

滚动轴承被称为“工业的关节”，广泛应用于铁路、汽车、轮船、航空航天、机械等领域，其检测技术的高低直接影响机械等产业的发展水平。轴承运行过程中发生故障时，各零件发生碰撞表现为非线性、非稳定性、复杂性的振动信号，而机械故障特征往往被包含在这些复杂的信号中。长期以来，从非线性、非稳定性的信号中提取机械故障特征信号的研究一直备受关注，因此旋转机械轴承故障特征提取和状态监测一直是工业界热点研究课题。随着信号降噪和分析能力的提高，利用信号降噪分析方法提取故障特征频率实现故障检测和诊断研究成为一个重要课题。

目前旋转机械故障诊断较为常见方法有时域方法、频域方法、小波分析[1-2]、经验模式分解[3]、包络解调、奇异值分解[4]、形态滤波分析等。通过振动信号的小波降噪与反向传播神经网络（back propagation neural network，BPNN）相结合可对滚动轴承的状态、故障及模式特征进行详细的分析与研究[5]。林近山等[6]将多重分形去趋势波动分析方法运用到轴承等旋转机械故障特征提取和识别应用中，研究表明该方法对旋转机械故障状态的变化较敏感，能够有效地将故障模式分离。YANG J等[7]将数学形态学与传统神经网络相结合，提出了形态学神经网络。这些方法虽取得一定效果，但由于轴承故障信号和噪声在频带上往往相互重叠，且淹没在其中，使处理具有较大难度，导致获取的故障信息包含故障特征冲击信号并伴有干扰信号。

数学形态学最早被用于二值图像处理，从集合的角度对二维信号进行分析，与几何关系相当密切[8]。吴小涛等[9-10]将形态学推广到多值函数的信号领域，通过本影变换将一般函数转换为集合，再运用二值形态学进行处理。针对形态滤波中结构元素尺度难以确定的问题，本文设计一种新的最优尺度判定指标以确定最优滤波算子。在确定形态优化滤波算子的基础上，考虑到轴承冲击信号分布在不同尺度中，将数学形态滤波结合粒子群最小二乘支持向量机（least square-support vector machines，LS-SVM），建立轴承故障识别分类模型，以期为旋转机械轴承质量安全检测提供一种有效的技术方法。

1 基本原理与方法

1.1 LS-SVM原理

LS-SVM建模基本思路：假设存在训练样本集D={（xi，yi）|i=1，2，3，…，n}，其中 xi∈Rn为输入数据，yi∈{-1，1}为输出数据。利用一非线性映射 φ（°）将样本数据投射到高维特征空间得到映射函数φ（x），通过结构风险最小化原则构造最优决策函数y=ωTφ（x）+β，其中 ω、β 为模型参数[11-12]。

利用结构风险最小化原则将求解ω、β模型参数问题转化为求解最优函数，可联立如下方程：

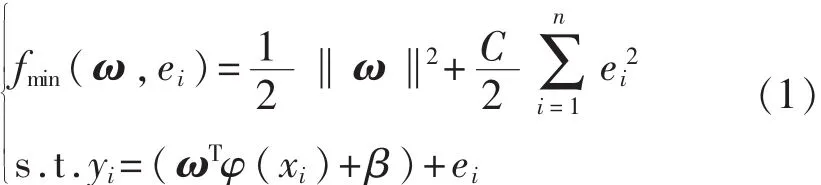
式中：ω——权向量；

β——偏差量；

ei——误差变量；

C——正规化参数；

φ（xi）——输入数据xi映射到高维特征空间对应的映射函数，i=1，2，…，n。

为求解ω、β，对上述方程式建立拉格朗日方程：

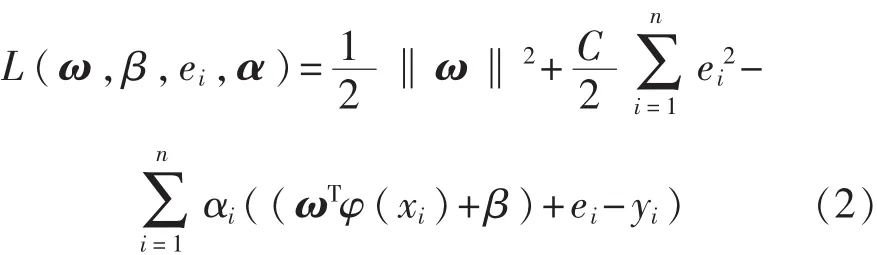
分别对 ω、β、ei、α 求偏导，式中 αi∈R 为 Lagrange乘子，可得线性系统：

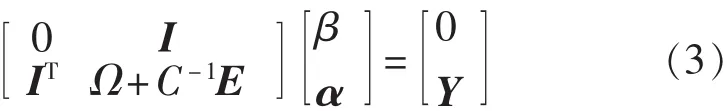
式中 I=[1，1，…，1]1×n，Y=[y1，y2，…，yn]T，α=[α1，α2，…，αn]，Ω={Ωi，j}=φ（xi）·φ（xj），Ei×j为单位矩阵。 定义核函数 K（xi，xj）=（φ（xi），φ（xj）），已知训练样本集 D={（xi，yi）|i=1，2，3，…，n}，由式（3）得 α、β，将 α 代入式（1），可得模型参数ω、β，求得决策函数为

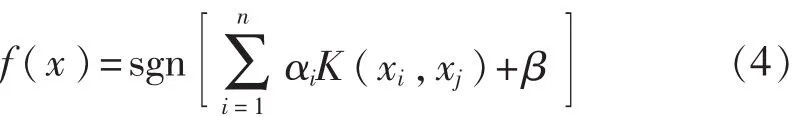
1.2 故障分析步骤

本次研究以自主搭建的轴承检测实验平台为基础，利用加速度传感器采集滚动轴承加速度信号，先对采集的原始信号进行预处理，再通过形态滤波优化算法对预处理信号进行降噪分析，然后将降噪后的信号分为训练样本和检验样本两部分，利用最小二乘支持向量机预测建模，最后通过计算预测均方误差值完成模型效果评价。轴承故障分析步骤如图1所示，主要包括信号采集阶段、滤波阶段、模型预测和模型效果评价4个部分组成。

在信号采集阶段，本文轴承实验样本由研究人员精心挑选，将各类故障样本分装入筒并贴上对应标签。轴承信号采集实验平台由轴承振动测试仪、采集卡、数据处理器和PC机构成。将轴承安装在测试仪上，主轴转动的同时传感器完成不间断采样，信号经过转换电路进入采集卡，再将信号输入数据处理器，PC机显示实时动态数据，利用LabVIEW编写的程序可以完成数据显示、保存和预处理。

在滤波阶段，采用形态滤波对振动信号进行降噪分析。针对传统形态滤波分析方法存在结构元素尺度自适应差的问题，本文选取峭度和偏斜度这两个对冲击信号较为敏感的变量，并定义判别指标J具体计算公式如下式所示，作为选取形态滤波结构元素尺度的依据：

式中 i=1，2， …，32，j=1，2， …，6，ki,j表示 i个尺度下，j类形态滤波算子所求得的峭度；li，j表示 i个尺度下，j类形态滤波算子所求得的偏斜度。

在确定形态滤波器种类的之前，首先拟定一系列结构元素尺度，以判别指标最大为选择标准。

预测建模过程中，为了体现本文方法的优越性，特选取支持向量机、反向传播神经网络和最小二乘支持向量机分别对原始信号、滤波信号进行预测建模，对模型预测结果进行统计分析。为了更加客观评价模型预测效果，采用计算预测均方误差和r2统计量标准对模型预测结果进行评价。

2 测试实例

2.1 信号采集

信号采集主要由两个部分实现：1）基于加速度传感器的原始信号采样模块；2）基于PC主机的信号分析模块。振动信号采集的基本流程如图2所示，基于加速度传感器的原始信号采样模块利用I/O传输采样原始信号，将振动信号经过测试放大器处理后，然后经过数据采集系统输入到PC机进行数据分析处理，主机接收并对信号进行分析，执行程序判断并下达操作指令。

2.2 滤波降噪分析

轴承外圈故障表现为外圈发生局部点蚀，将会导致滚动体每经过一次故障部位就产生振动冲击，从而引起外圈故障频率，相对其他故障类型轴承外圈故障样本表现类型较多。本文以轴承外圈故障为样本，利用自主搭建的轴承振动测振仪采集振动信号，然后利用判别指标最大选取的形态开-闭梯度滤波算子对原始振动信号进行降噪分析。

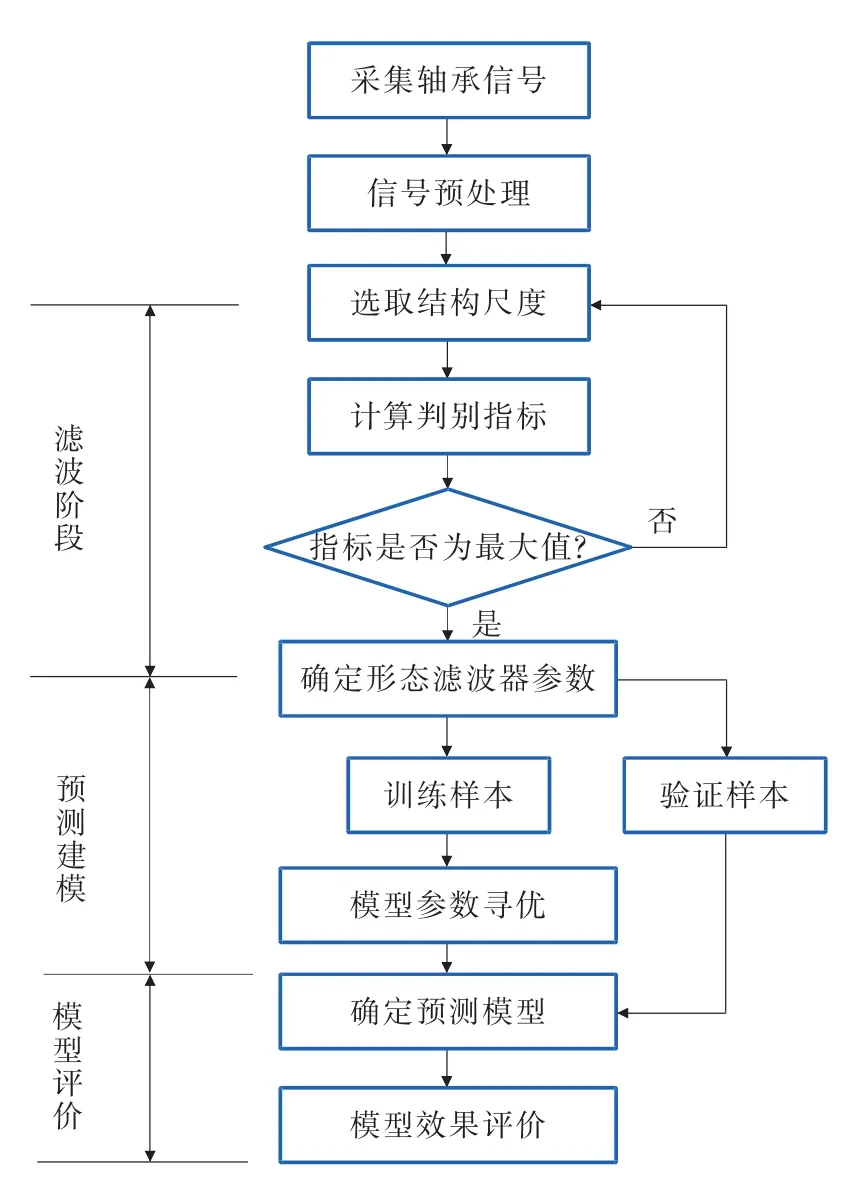
图1 轴承故障分析步骤图

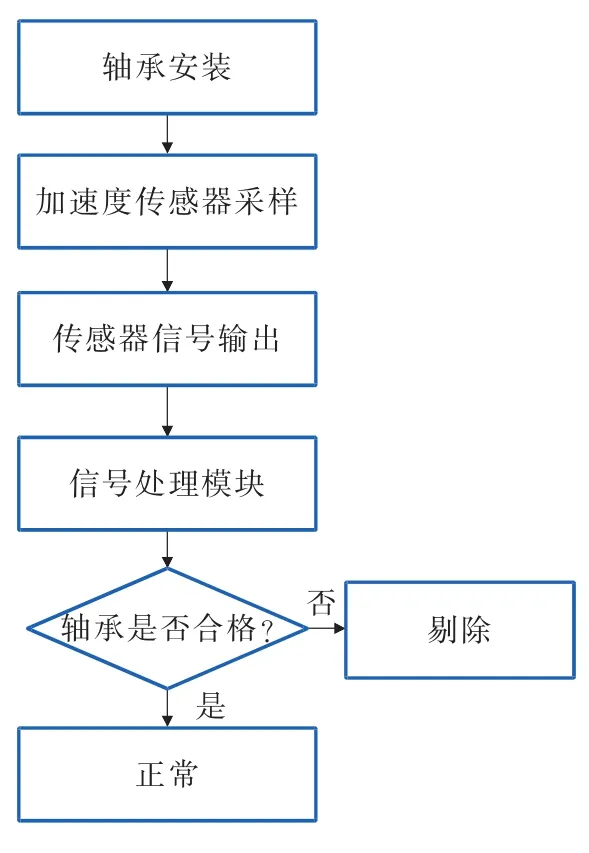
图2 信号采集流程图

原始轴承故障信号时域波形及频谱见图3。利用最优形态滤波算子对轴承外圈故障滤波分析频谱图见图4。从图3可以看出，轴承原始振动信号受噪声污染严重，无法直观从时域或者频域波形图中得到的故障频率。对比图3与图4，从时域上看，图4利用形态开-闭滤波时域波形轮廓更加清晰，抑噪效果更强。从频域来看，图4频谱图上低频段只保留了固有频率和特征频率及其倍频，并且冲击特征被增强，并且频谱图中特征频率及其倍频是连续的，抑噪效果明显[13]。

2.3 预测建模

形态滤波降噪分析可以有效抑制噪声，对于轴承故障明显的样本，也可以从故障频率识别轴承故障类型，但是对于微小故障样本，无法完成故障识别，故采用支持向量机（support vector machines，SVM）、LS-SVM和BPNN对滤波后的信号进行故障识别，并对各类预测模型结果分类讨论。为了验证本文方法的优越性，特选取包络解调分析、形态滤波分析和未处理的原始信号分别与3种建模方法组合，分类讨论3种建模方法在泛化能力、模型稳定性等方面的优缺点。

实验将150组轴承外圈故障振动信号分为两部分，一部分为训练集100组，其余为验证集。LS-SVM建模过程中，选取Gauss径向基核函数，大量研究表明，Gauss径向基核函数的SVM可以获得较好的稳定性和推广性[14]。再利用粒子群算法对C和σ进行参数寻优，得到C=76.21，σ=1.674，使用该参数进行轴承故障分类。

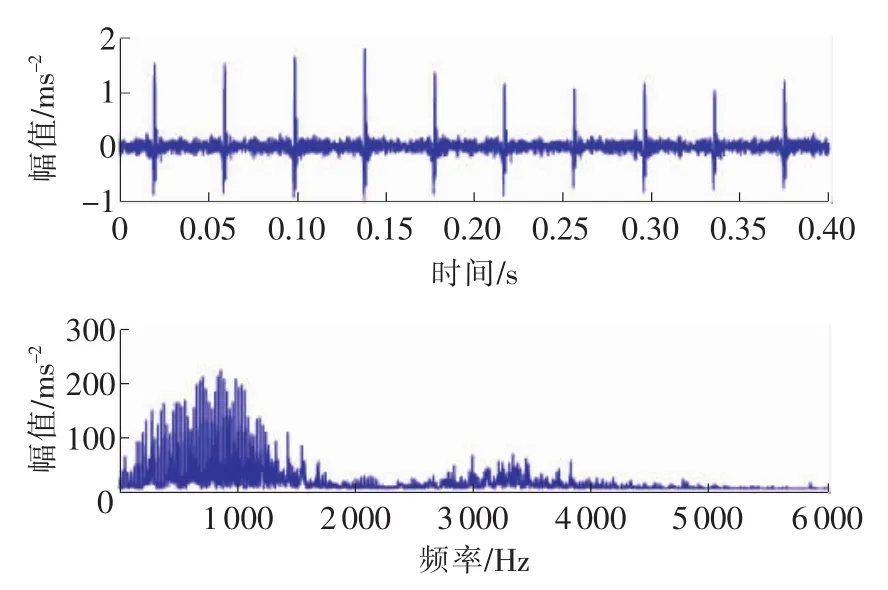
图3 原始轴承故障信号时域波形及频谱图

图4 形态优化滤波分析时域波形及频谱图

实验结果对比情况如表1所示。由表可得：采用形态滤波降噪分析时，LS-SVM方法对轴承外圈故障识别效果最优；通过包络解调降噪处理时，SVM故障识别结果最优；但是各降噪分析方法与BPNN组合，获得的诊断结果都不是很理想，主要是由于BPNN通过计算测试样本与训练样本之间的欧式距离来确定样本是否存在故障，容易造成数据误判。因此，LS-SVM和形态滤波组合、SVM和包络解调组合与其他故障诊断组合相比，故障识别准确率最高，但是LS-SVM和形态滤波组合相对于SVM和包络解调组合而言，支持向量机的个数较少，LS-SVM利用一组线性方程组求解，优于SVM复杂的二次线性方程求解，因此通过LS-SVM获得的模型稳定性更高，复杂度较低，使模型具有更好的泛化能力。

2.4 模型评估

预测建模的结果可以从预测准确度、模型稳定性以及模型泛化能力3个方面体现出来。为了更为客观地评估3种模型的预测结果，通过计算均方误差RMSE和r2统计量分别对3种模型预测结果进行定量分析，3种建模方法对比情况如表2所示。

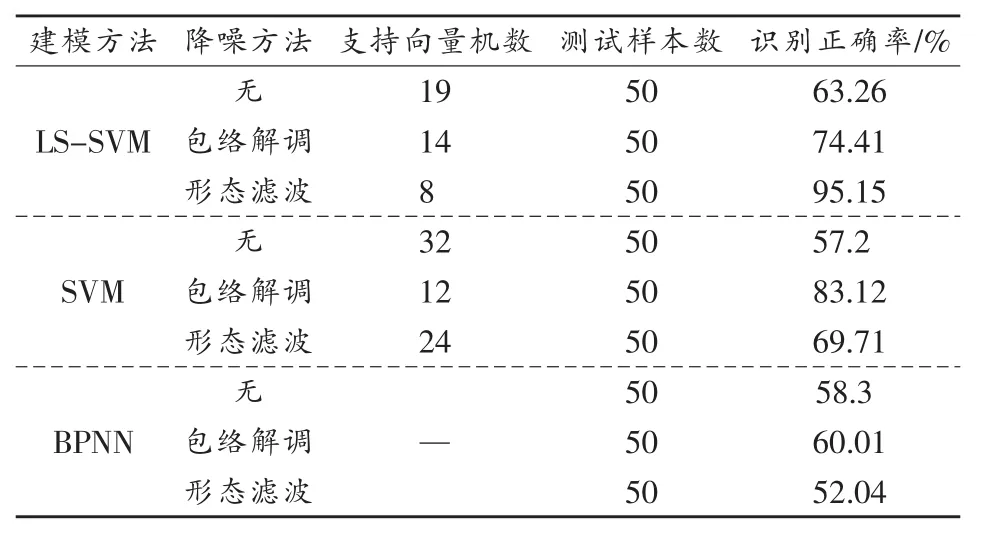
表1 不同降噪方法对轴承外圈故障诊断结果的对比情况

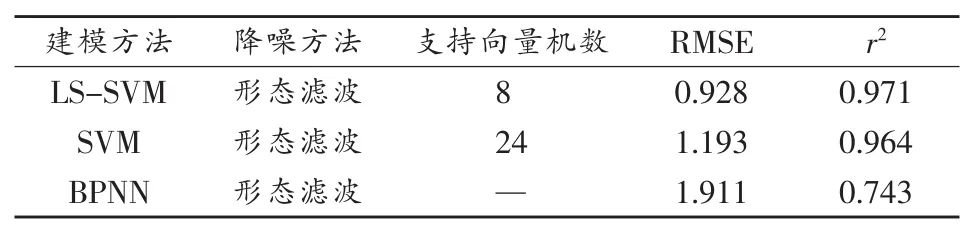
表2 3种建模方法RMSE和r2比较

从预测准确度、模型稳定性角度来看，SVM和LS-SVM模型预测结果不分上下，但是从模型复杂度的角度来看，LS-SVM模型更优，计算时间更短，从而简化模型复杂度，也有利于提高模型泛化能力。综合考虑，LS-SVM与形态滤波结合建模效果最理想，更适用于轴承振动故障分析。值得注意的是，上述形态滤波方法结合建模分析适用于滚动轴承应用分析，是否具有普遍实用价值还有待进一步讨论分析。

3 结束语

将本文将数学形态分析结合粒子群LS-SVM运用到轴承外圈故障信号中，实验结果表明：基于形态优化滤波的LS-SVM模型具有较好的稳定性、准确性，更具有模型结构简单等优点。与其他传统方法相比，形态优化滤波算法具有更好的噪声抑制功能，故障特征提取效果明显，LS-SVM模型泛化能力较佳，能够更好的实现轴承故障的准确诊断。

[1]毕艳兰，任小娜，彭丹，等.粒子群最小二乘支持向量机结合偏最小二乘法用于芝麻油质量的鉴别[J].分析化学，2013，41（9）：1366-1372.

[2]周绍磊，廖剑，史贤俊.RBF-SVM核参数选择方法及其在故障诊断中的应用[J].电子测量与仪器学报，2014，28（3）：240-246.

[3]陈绍炜，柳光峰，冶帅，等.基于蝙蝠算法优化ELM的模拟电路故障诊断研究[J].电子测量技术，2015，38（2）：138-141.

[4]DJURDJANOVIC D， NIJ， LEE J.Time-frequency based sensor fusion in the assessment and monitoring of machineperformancedegradation [C]∥New Orleans：American Society of Mechanical Engineers，2002：12-15.

[5]叶慧，罗秋凤，李勇.小波和多核SVM方法在UVA传感器故障诊断中的应用[J].电子测量技术，2014，37（1）：112-116.

[6]林近山，陈前.多重分形去趋势波动分析在滚动轴承损失程度识别中的应用[J].中国机械工程，2014，25（13）：1760-1765.

[7]YANG J， LI X， GUO W.A recognition of vehicle plate with mathematical morphology and neural networks[J].JournalofWuhan University ofTechnology，2001，25（3）：371-374.

[8]宋平岗，周军.基于形态滤波优化算法的滚动轴承故障特征提取方法[J].科学技术与工程，2014，14（2）：85-89.

[9]吴小涛，杨锰，袁晓辉，等.基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J].振动与冲击，2015（2）：38-44.

[10]汤井田，李晋，肖晓，等.基于数学形态滤波的大地电磁强干扰分离方法[J].中南大学学报（自然科学版），2012（6）：2215-2221.

[11]王建国，杨云中，秦波，等.基于峭度与IMF能量融合特征和LS-SVM的齿轮故障诊断研究[J].中国测试，2016，42（4）：93-97.

[12]顾燕萍，赵文杰，吴占松.最小二乘支持向量机的算法研究[J].北京：清华大学学报，2010，50（7）：1063-1066.

[13]桑迎平，蔡晋辉，曾九孙，等.基于形态优化滤波的轴承故障特征提取方法[J].电子测量与仪器学报，2016，30（5）：757-763.

[14]桑迎平.滚动轴承出厂检测与故障诊断研究[D].杭州：中国计量学院，2015.

（编辑：刘杨）

Bearing failure analysis based on improved morphological filtering and least square-support vector machine

RAO Jie，ZHANG Shaowang，XU Guangrong，ZHANG Yong
（Yunnan Institute of Measuring and Testing Techology，Kunming 650228，China）

In order to realize rolling bearing failure analysis，a method for diagnosis based on improved morphological filtering and least square-support vector machine is proposed.Firstly，confirm the optimal morphological filter by the maximum principle；then，the method is applied to bearing fault diagnosis by using optimalmorphologicalfilter； finally， using PSO-LSSVM to establish the model of bearing fault analysis.From the aspects of model stability，prediction accuracy and model complexity，the method has better experiment results.The results show that the method can effectively extract the bearing fault feature information.

rolling bearing；feature extraction；morphological filtering；least square-support vector machine；failure diagnosis

A

1674-5124（2017）04-0110-04

10.11857/j.issn.1674-5124.2017.04.023

2016-11-10；

2016-12-25

饶 杰（1963-），男，云南武定县人，高级工程师，主要从事计量检测相关工作。