基于FOA-GRNN的纳米铁粉分解炉温度预测
2017-07-18王盛慧秦石凌
王盛慧,秦石凌
(长春工业大学电气与电子工程学院,吉林 长春 130012)
基于FOA-GRNN的纳米铁粉分解炉温度预测
王盛慧,秦石凌
(长春工业大学电气与电子工程学院,吉林 长春 130012)
为提高纳米铁粉的制备工艺,实现纳米铁粉分解炉温度的精确控制,提出一种基于果蝇优化算法和广义回归神经网络的纳米铁粉分解炉温度预测方法。该方法采用现场采集数据,选取进液量和各个温区加热装置的开度因素来预测待预测温区温度。通过广义回归神经网络,建立温度预测模型,并利用果蝇优化算法对光滑因子进行动态寻优。选取不同种群规模对建立模型进行验证,并将该文建立模型与普通广义神经网络和粒子群算法优化的广义神经网络模型的预测效果进行对比。验证表明:该文建立模型平均相对误差为0.43%,且能够排除人为设置参数的干扰,具有较好的准确性与稳定性,可进一步用于分解炉温度控制的研究。
纳米铁粉;温度预测;果蝇优化算法;广义神经网络;光滑因子
0 引 言
纳米铁粉是一种新型纳米材料,在制造磁质材料、微波吸收材料以及医学等领域被广泛应用[1-2]。目前,工业生产纳米铁粉的主要手段为热解羰基铁法[3-4],其生产工艺要求非常苛刻,分解炉温度会直接影响分解炉的正常运行和纳米铁粉的最终品质[5]。
目前,国内关于热解羰基铁制备纳米铁粉的研究仍停留在原理与生产工艺上,并没有开展探究纳米铁粉分解炉温度预测模型这方面的研究[6-7]。因此,本文结合纳米铁粉生产过程中的分解运行参数,建立了纳米铁粉分解炉温度预测模型,为进一步实施系统优化控制奠定了理论基础。
广义回归神经网络模型(general regression neural network,GRNN)已成功用于其他模型的建立当中,并表现出较为精确的预测效果[8-9]。因此,本文引入GRNN对纳米铁粉分解炉温度进行预测,并引入果蝇优化算法(fruit fly optimization algorithm,FOA)对 GRNN模型进行改进。首先,分析并选择影响纳米铁粉分解炉温度的主要因素,采用吉恩镍业公司纳米铁粉生产线的现场数据,利用GRNN建立温度预测模型。然后为降低人为因素对预测结果的影响,利用FOA对GRNN的输入参数进行动态寻优。最后为验证模型的稳定性与准确性,将FOA-GRNN模型与普通GRNN模型和粒子群算法(particle swarm optimization,PSO)优化的GRNN模型预测结果进行对比。
1 算法原理与步骤
1.1 GRNN模型
GRNN是由美国研究员Donald F.Specht[10]提出的一种基于非线性回归理论的神经网络模型。GRNN容错性高,拟合效果好,非线性映射能力强,因此适用于非线性模型的建立[11]。
GRNN网络结构由输入层、模式层、求和层和输出层构成。输入层用来接收输入变量 X=(x1,x2,…,xn)T。模式层接收输入层信息后,将信息通过传递函数Pi转换并传递至求和层,其传递函数Pi为
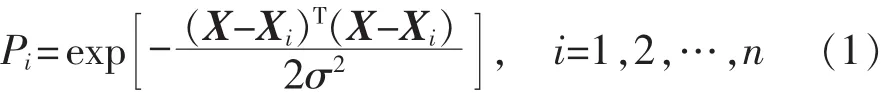
式中:n——训练样本个数;
σ——光滑因子。
求和层接收由模式层经过式(1)转换的输入信息,并对神经元进行两类求和。
一类神经元的求和公式为
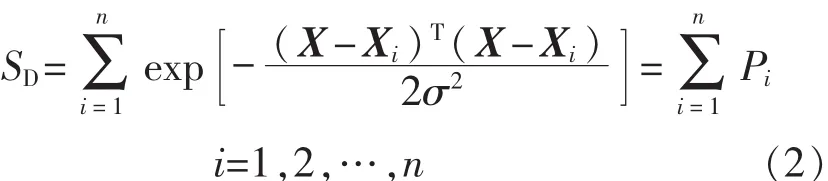
另一类神经元的求和公式为
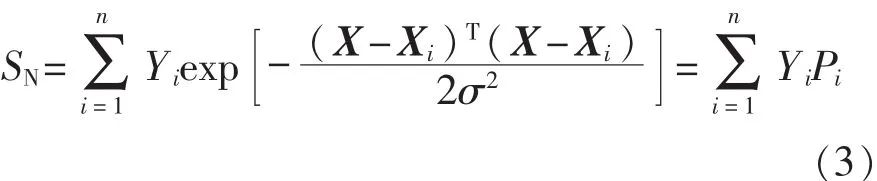
式中Yi为第i个神经元基于输入Xi的实际值。
输出层接收求和层传递的两类神经元求和,并输出最终数学期望:

GRNN模型结构简单,学习样本确定的情况下只有一个参数,即光滑因子σ需要人为确定。因此,GRNN模型很大程度上减少了人为因素带来的影响。一般而言,当光滑因子σ较大时,GRNN模型拟合效果较好,但此时需要较多的神经元来确保适应函数快速变化的准确性,也就意味着需要更多的学习样本。当光滑因子σ较小,甚至趋近于0时,GRNN的泛化能力将大幅下降,导致预测结果不理想。目前光滑因子σ的选取采用随机初始化后手工调整的方法,收敛速度慢且精度较差。本文采用FOA对光滑因子σ进行动态调整,避免人工误差,从而优化了GRNN模型。
1.2 FOA-GRNN模型
果蝇优化算法是我国台湾潘文超教授[12-13]在2011年提出,通过模拟果蝇觅食行为,推导出寻求全局最优解的进化算法。果蝇能够嗅到食物源,FOA算法实现简单,收敛速度快,精准度高,因此,本文采用FOA动态调整GRNN中的光滑因子σ,从而优化传统的GRNN模型,取得了更好的预测效果[14-15]。
FOA优化的实质就是各个果蝇搜寻最佳味道浓度,并通过迭代寻找到全局最优味道浓度。每个果蝇个体都有自己对应的坐标值(X,Y),表示该果蝇个体的飞行方向和距离,其味道浓度判定值S:

将味道浓度判定值S代入判定函数可以得到该果蝇个体的味道浓度,并与最佳值比对进行迭代。整个迭代过程通过两种最佳味道浓度来更新,一种为个体最佳味道浓度,即果蝇个体在某一次迭代中能够找到的最佳味道浓度;另一种为全局最佳果蝇个体,即整个果蝇群体能够找到的最佳味道浓度。
果蝇个体位置的更新公式为

式中:Xi、Yi——第i个果蝇个体的飞行方向与距离;
X、Y——之前迭代寻找到的最佳味道浓度对应的果蝇坐标;
RV——随机值。
本文利用FOA对GRNN的模型参数,即光滑因子σ进行动态寻优,并在4折交叉验证的基础上,采用训练样本误差的均方差均值作为寻优适应度值。FOA优化GRNN的适应度函数Function的Matlab伪代码如下:
1)初始化交叉验证分组,每次交叉验证获得的误差均方差以及4折交叉验证后的均方差均值:
2)训练样本输入数据与预测数据归一化:
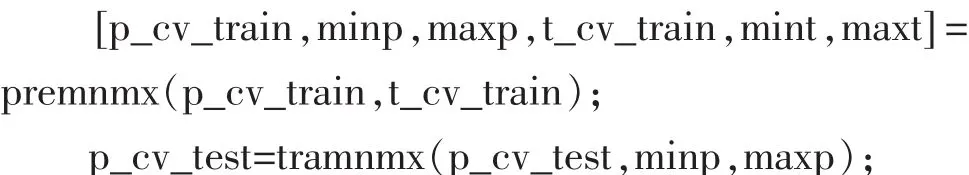
3)将归一化后的样本输入和主程序传递的光滑因子值代入GRNN计算预测输出:
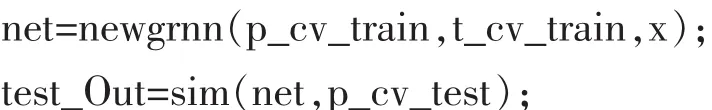
4)训练集集样本反归一化:
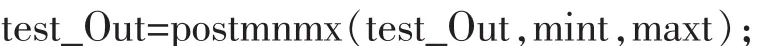
5)计算预测数据与实际输出的误差及误差均方差:

6)计算4组交叉验证训练样本的平均均方差,并返回给主函数:
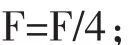
2 结果与分析
2.1 纳米铁粉分解炉结构
纳米铁粉分解炉结构如图1所示,由4段温区级联而成,每段温区都要求在合适的指标范围内。不同温区的温度会产生耦合,因此,在预测某一温区温度时,需考虑其他温区的即时温度。基于以上分析,本文以预测第1段温区温度为例,选择羰基铁液体进液量 (liquid flow rate,LR)、4段加热装置的开度与其他温区的温度,利用FOA-GRNN来建立纳米铁粉分解炉温度预测模型。
2.2 模型验证
为测试本文建立模型的准确性,选取吉恩镍业公司工程实际的36组数据作为模型的学习样本进行验证。根据进液量 LR(30,40,50 L·h-1)将数据分为3类,每类随机选取8组数据共24组数据作为训练样本,剩余每类4组共12组数据作为测试样本。
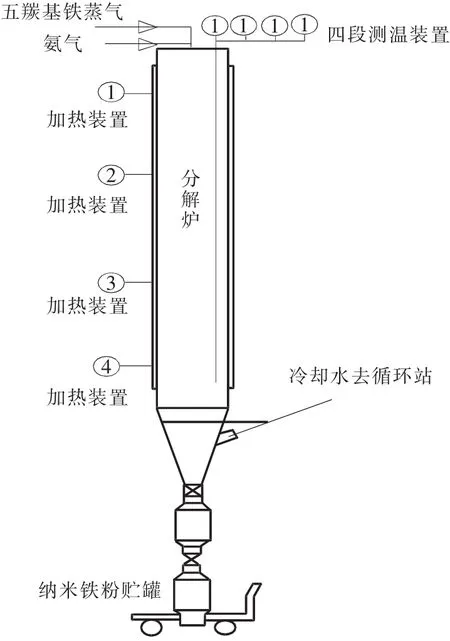
图1 纳米铁粉分解炉结构图
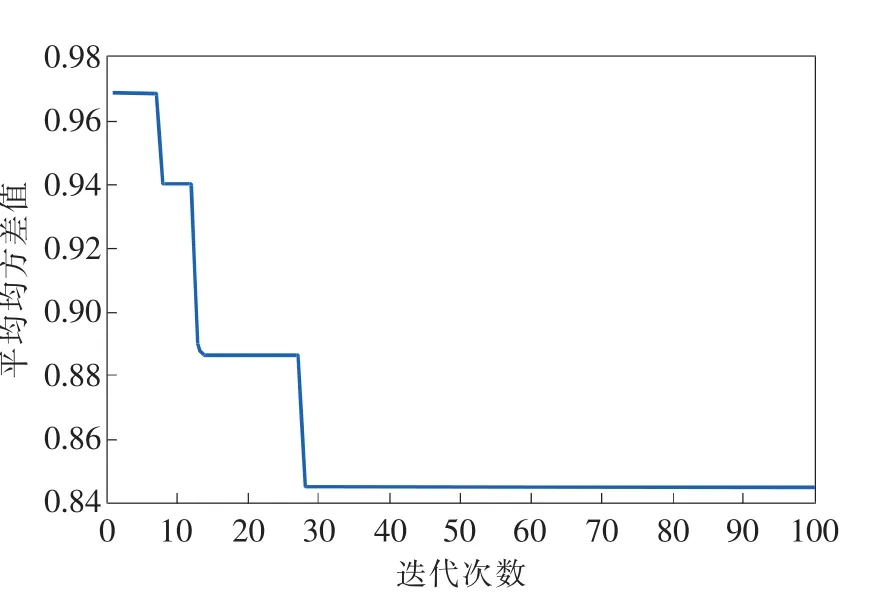
图2 FOA-GRNN收敛曲线图
设置迭代参数为 100,种群规模为 20,进行FOA-GRNN模型训练,并以训练集进行4折交叉验证得到的误差平均均方差值最为适应度函数来寻找最优光滑因子σ,FOA-GRNN寻优的收敛曲线如图2所示。
FOA-GRNN搜寻到的最低平均均方差值为0.8451,此时最佳光滑因子σ为0.4737。
以FOA-GRNN搜寻到的最佳光滑因子σ与12组测试样本中的进液量LR,4段温区电加热装置的开度O1、O2、O3和O4以及其他温区温度 T2、T3和T4作为GRNN模型的输入向量,来预测T1的温度,预测结果见表1。由表中结果可见,本文采用的FOA-GRNN模型能够较为准确地预测纳米铁粉分解炉温度,其最大绝对误差为-1.84℃,最大相对误差为0.71%,平均相对误差为0.43%,低于国内羰基铁热解温度控制精度要求,且温度预测稳定性较强,显示了较好的预测效果。
为验证种群规模对FOA-GRNN优化结果的影响,本文另选取种群规模为40和60时进行仿真,预测纳米铁粉分解炉温度预测,FOA-GRNN搜寻到的最佳光滑因子σ、对应的训练样本平均均方差值、搜寻到最佳光滑因子σ时的迭代步数以及预测结果平均相对误差见表2。
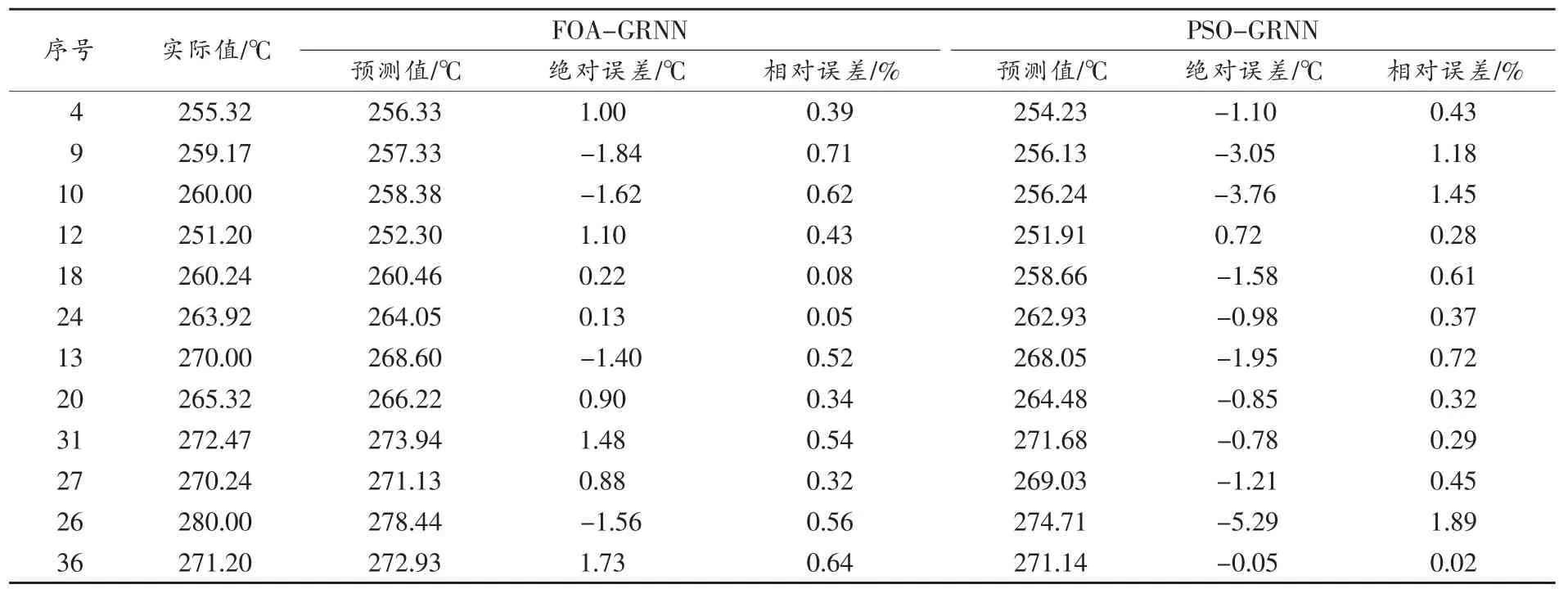
表1 FOA-GRNN和PSO-GRNN纳米铁粉分解炉温度预测结果对比
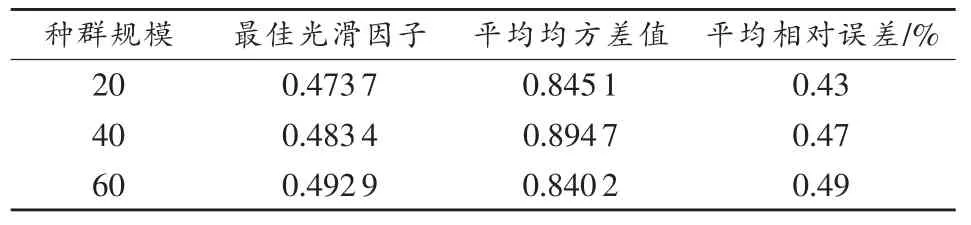
表2 不同种群规模对FOA-GRNN模型的影响
将表中结果对比可见,FOA-GRNN的初始参数种群规模对结果的影响很小,基于FOA-GRNN的纳米铁粉分解炉温度预测较为准确,对FOA的初始参数设置并不敏感。
2.3 FOA-GRNN模型与其他模型对比
本文选用FOA-GRNN建立纳米铁粉分解炉温度预测模型,为验证模型的优越性,选取普通GRNN模型和PSO-GRNN模型与本文建立模型进行对比。为体现模型优劣对比的公平性,在模型建立时,选取与建立FOA-GRNN温度预测模型时相同的训练集与预测集。

表3 普通GRNN温度预测结果
首先,由于普通GRNN模型的光滑因子σ需要人为确定,因此建立模型时选取如表3所示σ作为普通GRNN的光滑因子σ值,构建普通GRNN模型,其预测结果见表3。
由表中结果可见,使用普通GRNN建立纳米铁粉分解炉温度预测模型,由于光滑因子σ无法确定,温度预测结果不准确,误差偏大。而本文采用FOA对GRNN的光滑因子σ进行动态寻优,能够准确搜寻到最佳光滑因子σ,从而实现准确预测,提高了模型的稳定性。
最后,选取PSO-GRNN模型与本文所建立模型进行对比。设置迭代参数为100,种群规模为20,学习因子为1.5,并以训练集进行4折交叉验证得到的误差均方差平均值作为适应度函数来寻找最优光滑因子σ,PSO-GRNN寻优的收敛曲线如图3所示。
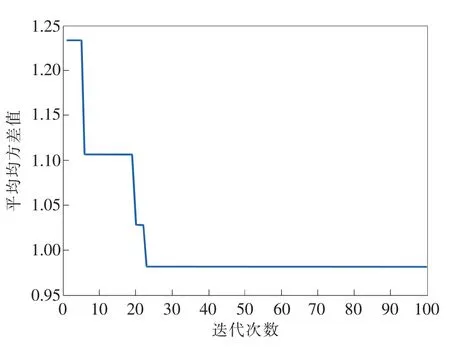
图3 PSO-GRNN收敛曲线图
PSO-GRNN搜寻到的最低平均均方差值为0.9817,此时最佳光滑因子σ为0.7563。与本文采用的FOA-GRNN相比,搜寻到的最低均方差均值较大,收敛精度较低。PSO-GRNN预测结果见表1,由表中结果可见,选取PSO-GRNN建立纳米铁粉分解炉温度模型,其最大误差为-5.29℃,最大相对误差为1.89%,平均相对误差为0.67%,最大绝对误差和最大相对误差约为FOA-GRNN模型的3倍,预测稳定性较差,且误差偏高,预测结果较差。
3 结束语
1)本文介绍了纳米铁粉分解炉的工作流程,并以预测一段分区温度为例,选取羰基铁液体进液量LR、各分段温区电加热装置的开度、其他分段温区的温度作为GRNN的输入变量,建立了纳米铁粉分解炉温度预测模型。
2)以训练样本进行4折交叉验证后神经网络输出与实际值误差的平均均方差值为适应度函数,采用FOA对光滑因子σ进行动态寻优,能够排除人为选取光滑因子σ的随意性,降低了人为因素对温度预测效果的干扰。实验验证表明,基于本文建立模型的纳米铁粉分解炉温度预测平均相对误差可以达到0.43%,而最大绝对误差为1.84℃,远低于业界标准。
3)选取不同种群规模构造FOA-GRNN模型,实验表明,采用20,40,60作为种群规模初始值时,平均相对误差分别为0.43,0.47,0.49,显示模型对初始参数并不敏感,体现了模型的稳定性。将本文建立的基于FOA-GRNN的纳米铁粉分解炉温度预测模型与普通GRNN模型及PSO-GRNN模型的预测效果进行对比。GRNN的σ值需要人为选定,受人因素干扰较大,且无法准确找到最佳值。PSO-GRNN的平均相对误差为0.67%,高于FOA-GRNN模型,表明FOA-GRNN温度预测模型具有更好的稳定性与准确性。
[1]秦明礼,黄敏,曲选辉,等.一种制备纳米铁粉的方法:201410785486.4[P].2014-12-17[2016-07-05].
[2]SURHONE L M, TENNOE M T, HENSSONOW S F,et al.Nano Iron Powder[M].Betascript Publishing,2011:97-105.
[3]穆冀里,蒋武锋,董建君,等.纳米铁粉的制备方法研究[J].粉末冶金工业,2014,24(2):33-37.
[4]李永军,张强林,谭世雄,等.一种纳米铁粉的生产方法:200610145351.7[P].2006-11-24[2016-07-05].
[5]赵东龙.羰基铁电热分解器温度控制系统研究[D].长春:长春工业大学,2015.
[6]吴栋,韦建军,唐永建,等.纳米铁粉制备方法的研究[J].四川大学学报(自然科学版),2008,45(2):352-356.
[7]何叶.纳米铁粉制备方法研究及应用[D].广州:广东工业大学,2009.
[8]黄鑫,赵捍东.基于广义回归神经网络的弹丸落点预报方法[J].测试科学与仪器(英文版),2016,7(1):7-12.
[9]ROOKI R.Application of general regression neural network (GRNN) for indirect measuring pressure loss of Herschel-Bulkley drilling fluids in oil drilling[J].Measurement,2016(85):184-191.
[10]SPECHT D F.A general regression neural network[J].IEEE Transactions on Neural Networks,1991,2(6):568-576.
[11]王小川.Matlab神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013:57-63.
[12]潘文超.果蝇最佳化演算法[M].台北:沧海书局,2011:25-28.
[13]XING B, GAO W J.Fruit fly optimization algorithm[M]∥Innovative Computational Intelligence:A Rough Guide to 134 Clever Algorithms.Berlin:Springer International Publishing,2014:167-170.
[14]PAN W C.A new fruit fly optimization algorithm:taking the financial distress model as an example[J].J Knowledge-Based System,2012,26(3):69-74.
[15]LIN S M.Analysis of service satisfaction in web auction logistics service using a combination of fruit fly optimization algorithm and general regression neural network[J].Neural Computing&Applications,2013,22(3-4):783-791.
(编辑:刘杨)
Temperature prediction of nano-iron powder decomposing furnace based on FOA-GRNN
WANG Shenghui,QIN Shiling
(School of Electrical and Electronic Engineering,Changchun University of Technology,Changchun 130012,China)
A new method based on fruit fly optimization algorithm (FOA) and generalized regression neural network(GRNN) is put forward in this paper to improve the manufacturing technologyofnano-iron powderand realizetheaccurate controlofthe nano-iron powder decomposing furnace temperature.Field data like liquid flow rate and opening value of each temperature zone are selected to predict the temperature based on GRNN.The smooth factor of which is dynamically optimized with FOA,and the temperature prediction model is set up.The model with different population sizes is validated by field data in this paper and its predication performance is compared with GRNN and PSO-GRNN.The experiments show that the average relative error is 0.43%and the interference of setting parameters can be excluded which shows the accuracy and stability of FOA-GRNN model.The model can be further used in the study of nano-iron powder decomposing furnace temperature control.
nano-iron powder; temperature prediction; fruit fly optimization algorithm; general regression neural network;smooth factor
A
1674-5124(2017)04-0100-05
10.11857/j.issn.1674-5124.2017.04.021
2016-08-19;
2016-09-25
吉林省重点科技攻关项目(20140204024GX)
王盛慧(1976-),女,吉林吉林市人,副教授,硕士,研究方向为电力系统故障检测、数字传动与电力节能技术。
