一种计算三芯电力电缆表面磁场的解析方法

李世松，袁燕岭，董 杰，甘景福，黄松岭，赵 伟

（1.清华大学电机系，北京 100084；2.国网唐山供电公司，河北 唐山 063000）

一种计算三芯电力电缆表面磁场的解析方法

李世松1，袁燕岭2，董 杰2，甘景福2，黄松岭1，赵 伟1

（1.清华大学电机系，北京 100084；2.国网唐山供电公司，河北 唐山 063000）

因三芯电力电缆稳态运行时传输的三相电流之和为0，以传统的电流互感器无法测量出其中各芯线即各相电流，该文从表征通流状态下三芯电力电缆中各处电磁特性的电磁场方程出发，提出一种三芯电力电缆表面磁场的解析计算方法，其不仅适用于对称三芯电缆，还适用于其他电缆三芯任意分布的情形。基于该解析算法，通过测量三芯电缆表面的磁场，就可以较准确地实现对三芯电力电缆各芯线电流的测量。以该解析模型进行计算和采用有限元仿真模型计算的结果均表明，所提出解析算法具有较好的准确性，对构建新型电缆在线监测系统具有理论指导价值。

电力电缆；磁场计算；解析模型；电流测量

0 引 言

近年来，随着电缆制作工艺的不断进步，电缆输配电工程获得了长足发展[1]。一般地，35 kV以上的三相电力系统电缆输配电工程多采用单芯电缆，而35kV以下的三相电力系统电缆输配电工程则多采用三芯电缆[2]。由于电缆运行环境复杂，发生故障后很难及时排查和检修，因此，电力电缆运行的安全性越来越受到重视[3]。

为确保电力电缆供电的可靠性，十分需要对电力电缆的运行状态实施在线监测。但目前国内外已有的电力电缆在线监测方法，大多是通过测量间接反映电缆运行特性的相关参数实现的，例如对电缆温度、老化等参数进行在线测量等[4-11]。间接测量往往存在较大延迟，且大多数间接测量方法不能确诊电缆运行故障的位置和类型，存在较大局限性。

为了更直接地实现对三芯电力电缆运行状态的监测，一种较为可靠的方法，是对实际运行中电缆各芯线的电流即三相系统的各相电流进行测量。对单芯电缆，相电流测量原理与一般的穿心电流互感器无异。但对于三芯电缆而言，其在稳态运行时，三相电流之和为零，因而穿过电缆表面任意横截面的总磁通也为零，故不能用传统感应式方法测量相电流。

为了解决以传统感应式电流测量装置无法测量出三芯电力电缆各相电流的难题，文献[12]提出了一种基于磁传感器测量对称三芯电缆相电流的新方法，即通过测量三芯电力电缆表面周向磁场的变化来实现对对称三芯电力电缆中各相电流的有效测量。但文献[12]仅给出了电缆中三根芯线对称的情形，而实际输电工程应用中的三芯电缆，三芯分布受电缆类型、电缆加工工艺水平等影响，未必满足三芯对称的条件。电缆三芯非对称情况若仍采用文献[12]中的模型，势必会造成测量结果的不准确。鉴于此，本文试提出一种更为普遍的三芯电力电缆表面磁场解析模型及其计算方法，旨在将文献[12]中论及的电缆三芯对称的情形推广至三芯任意分布的情形。如此，可更普遍地指导基于磁传感器的三芯电力电缆相电流的测量。

1 三芯电缆表面磁场计算解析模型

建立解析模型所使用的三芯电缆的结构见图1，其中，电缆中心为O，A、B、C分别是电缆各芯线的位置，电缆中心到A、B、C芯线的距离分别为r1、r2和r3。不失一般性，可设y轴与OA重合，则A点的坐标为（0，r1）。 电缆中心到 B、C两芯线的矢量，即OB、OC与x轴的夹角分别为α、β，故B点的坐标为（r2cosα，r2sinα），C 点的坐标为（r3cosβ，r3sinβ）。

计算时，A、B、C 三相电流分别为 IA、IB和 IC。SA、SB、SC分别为OA、OB、OC延长线与电缆表面的交点，亦即磁传感器的安装位置。SA、SB、SC到电缆中心的半径为R。根据安培环路定理，A相电流IA在SA处产生的磁感应强度为

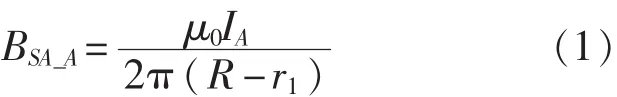
其中μ0为真空磁导率。

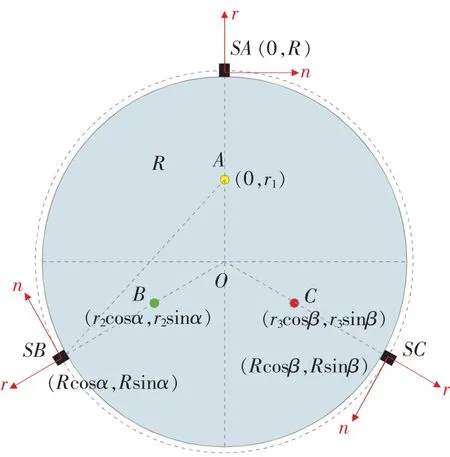
图1 三芯电力电缆结构及各相电流的测量原理示意

方便起见，定义磁传感器沿圆周方向为n，沿径向方向为r，如图1所示。显然，式（1）中的磁场方向全部为n分量。类似地，B相电流IB在SA处产生的磁感应强度为

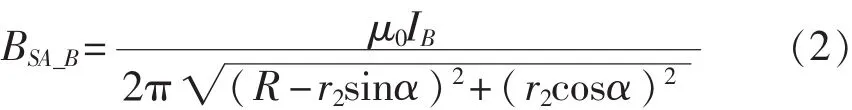
式（2）所示的磁感应强度BSA-B的方向为

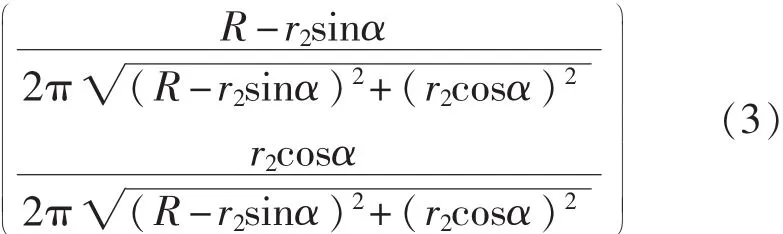
故BSA-B沿n方向和r方向的分量分别为

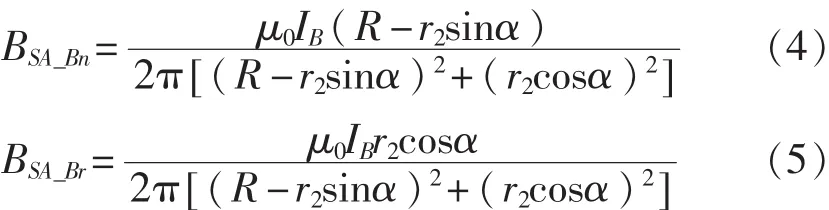
同理，C相电流IC在SA处产生的磁感应强度为

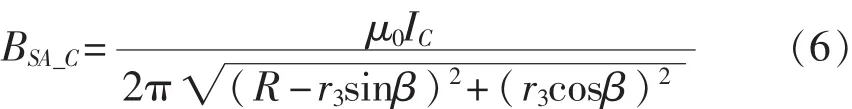
BSA-C沿n方向和r方向的分量分别为

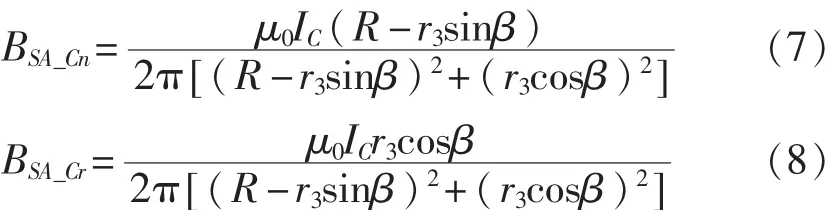
联立式（1）、式（4）和式（7），可得 SA 处磁感应强度沿n方向的分量为

联立式（5）和式（8），可得SA处磁感应强度沿r方向的分量为

在求解SB、SC处的磁感应强度时，可将x和y坐标轴进行旋转。例如求解SB处的磁感应强度时，将y轴旋转至与OB重合。此情况下，OC、OA与x轴的夹角分别为 β-α+90°、180°-α。用 β-α+90°、180°-α分别替代式（9）和式（10）中的α和β，并轮换相应的相电流和 ri（i=1，2，3），可得到 SB 处的磁感应强度沿n方向和r方向的分量分别为

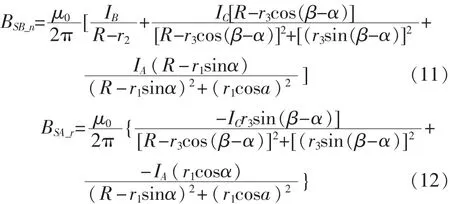
同理，计算SC处的磁感应强度时，将y轴旋转至与OC重合，OA、OB与x轴的夹角分别为180°-β、α-β+90°。 用 180°-β、α-β+90°分别替代式（9）和式（10）中的 α 和 β，并轮换相应的相电流和 ri（i=1，2，3），可得SC处磁感应强度沿n方向和r方向的分量分别为

2 模型仿真验证

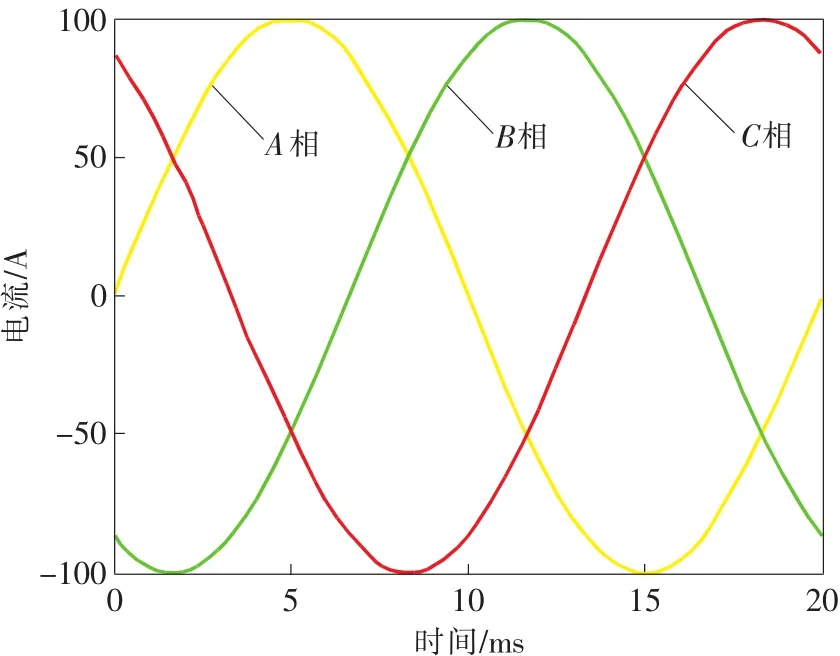
图2 计算实例1中A、B、C三相电流的波形

图3 计算实例1中SA、SB、SC处以解析模型计算出的磁感应强度与有限元仿真计算结果的对比

图4 计算实例1中SA、SB、SC处以解析模型计算出的磁感应强度沿电缆表面切向分量与有限元仿真计算结果的对比

为验证所构建解析模型的正确性，采用两个计算实例，并将所建立的解析模型与有限元仿真计算结果进行比对。计算实例1为对称模型，参数设置如下：R=45 mm，r1=r2=r3=20 mm，IA=IB=IC=100 A，α=210°，β=330°；A、B、C 三相芯线的半径均为 12.5mm。

图2为A、B、C三相工频正弦电流的波形；图3为SA、SB、SC 3个磁场极值点处的磁感应强度解析模型与有限元仿真计算的结果对比；图4为SA、SB、SC 3个磁场极值点处的磁感应强度沿电缆表面切向即n方向分量的解析模型与有限元仿真计算的结果对比；图5为SA、SB、SC 3个磁场极值点处的磁感应强度沿电缆表面垂直方向即r方向分量的解析模型与有限元仿真计算的结果对比。

从图3～图5不难看出，计算实例1中，解析模型与有限元仿真的计算结果非常一致，很好地验证了所构建的解析模型在电力电缆三芯对称情况下的准确性。

为定量说明计算实例1中解析算法的准确性，表1给出本文解析算法与有限元仿真模型的计算结果（SA、SB、SC处磁感应强度及其沿电缆表面的切向和垂直分量）之间最大差量的绝对值。可见，采用本文提出的解析计算模型与有限元仿真模型计算所得三芯电缆表面磁场最大差量的绝对值均小于0.03mT，完全满足三芯电缆在线监测的准确性要求。

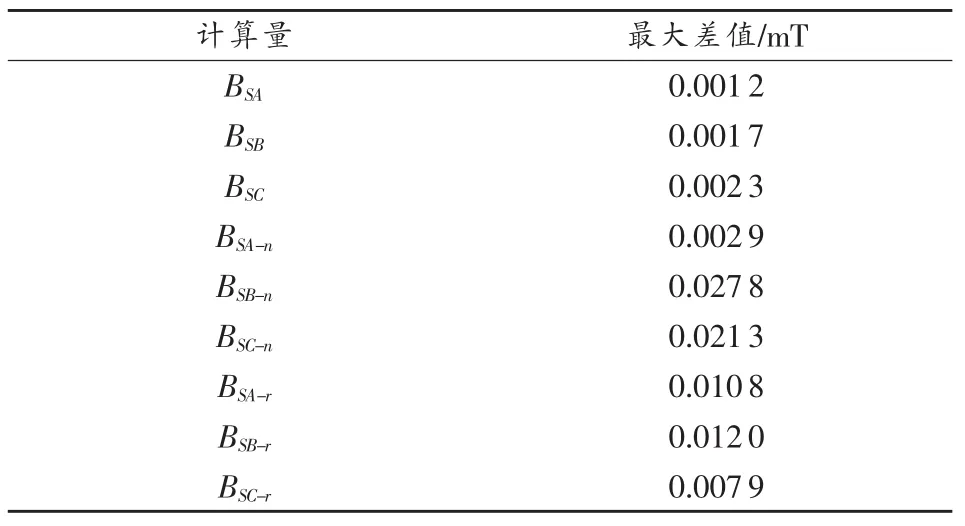
表1 计算实例1的解析算法与有限元仿真模型的计算结果之间最大差量的绝对值

计算实例2为非对称模型，具体参数设置如下：R=45mm，r1=20mm，r2=28.28 mm，r3=25 mm，IA=IB=IC=100A，α=225°，β=323.13°；A、B、C 三相芯线半径均为12.5mm。

图6 计算实例2中SA、SB、SC处以解析模型计算出的磁感应强度与有限元仿真计算结果的对比

图7 计算实例2中SA、SB、SC处以解析模型计算出的磁感应强度沿电缆表面切向分量与有限元仿真计算结果的对比

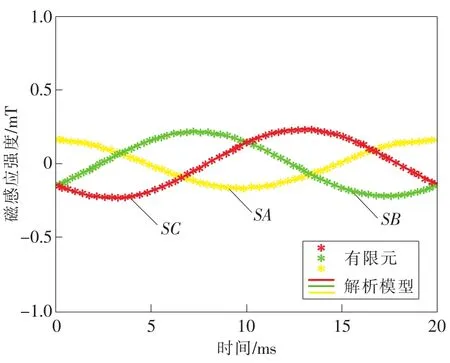
图8 计算实例2中SA、SB、SC处以解析模型计算出的磁感应强度沿电缆表面垂直分量与有限元仿真计算结果的对比

计算实例2仍采用图2所示的三相工频正弦电流波形；图6为SA、SB、SC 3个磁场极值点处以解析模型计算出的磁感应强度与有限元仿真计算结果的对比；图7为SA、SB、SC 3个磁场极值点处以解析模型计算出的磁感应强度沿电缆表面切向即n方向的分量与有限元仿真计算结果的对比；图8为SA、SB、SC 3个磁场极值点处以解析模型计算出的磁感应强度沿电缆表面垂直方向即r方向的分量与有限元仿真计算结果的对比。

从图6～图8可见，计算实例2中，解析模型与有限元仿真的计算结果也非常一致，如此，就验证了所提出解析模型在电力电缆三芯非对称情况下的正确性。类似地，表2给出了计算实例2中以本文提出的解析算法进行计算，与利用有限元仿真模型计算结果（SA、SB、SC处磁感应强度及其沿电缆表面的切向和垂直分量）之间最大差量的绝对值。可见，两模型计算所得三芯电缆表面磁场的最大差量的绝对值均小于0.02mT，完全满足三芯电缆在线监测的准确性要求。

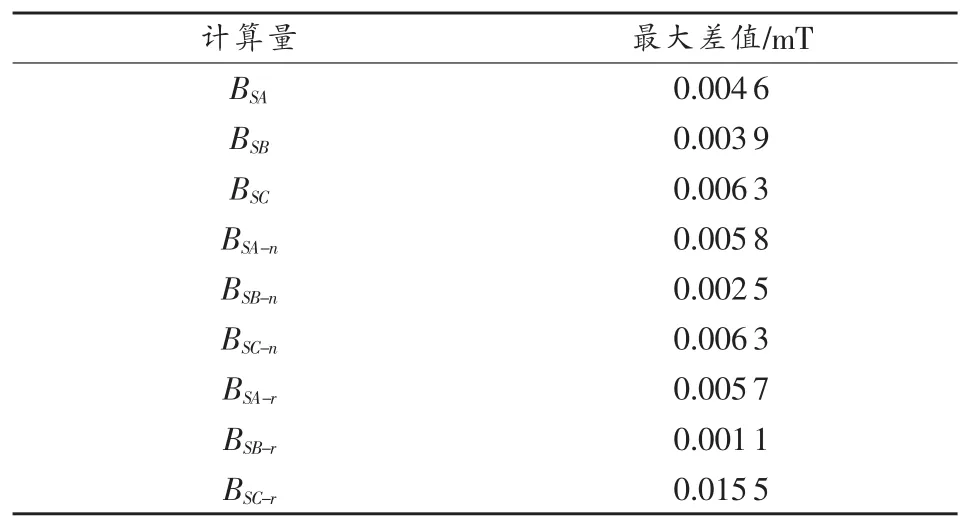
表2 计算实例2以解析算法与有限元仿真模型计算出结果之间最大差量的绝对值

3 结束语

针对文献[12]中基于磁传感器测量三芯电缆相电流法仅适用于电缆三芯对称的情形，本文提出了一种更为普遍适用的三芯电力电缆表面磁场解析计算方法，其可将电缆三芯对称推广至更为普遍的任意分布的情形。通过有限元仿真计算，很好地验证了所建立解析模型的正确性。

所提出的解析模型，明确了磁传感器的输出量与三芯任意分布的电力电缆各芯线电流之间的量值关系，对基于磁传感器原理、芯线非对称分布三芯电力电缆的相电流测量和运行状态监测均具有指导价值。

[1]BARBER K W，MARAZZTO H.Reliable undergrounding of electricity supply in Asia[C]∥Asia Pacific Conference on MV Power Cable Technologies Kuala Lumpur Malaysia，2005：1-5.

[2]韩立奎，王海涛，韩晓冰.电缆设计中三芯与单芯电缆的选择与比较[J].电线电缆，2011，5（5）：15-16.

[3]袁燕岭，李世松，董杰，等.电力电缆诊断检测技术综述[J].电测与仪表，2016（9）：1-7.

[4]OYEGOKE B，HYVONEN P P，ARO M，et al.Application of dielectric response measurement on power ca ble systems[J].IEEE Transactions on Dielectrics and Electrical Insulation，2003（5）：862-873.

[5]JONES S， BUCEA G， MCALPINE A， et al.Condition monitoring system for transGrid 330 kV power cable[C]∥IEEE International Conference on Power System Technology，2004（2）：1282-1287.

[6]彭超，赵健康，苗付贵.分布式光纤测温技术在线监测电缆温度[J].高电压技术，2006，32（8）：43-45.

[7]刘刚，张高言，周凡.基于等温松驰法的110kV高压电缆老化状况评估[J].高电压技术，2014，40（2）：497-504.

[8]郭灿新，张丽，钱勇，等.XLPE电力电缆中局部放电检测及定位技术的研究现状[J].高压电器，2009，45（3）：56-60.

[9]钱勇，黄成军，江秀臣，等.基于超高频法的GIS局部放电在线监测研究现状及展望[J].电网技术，2005，29（1）：40-43.

[10]周远翔，赵健康，刘睿，等.高压/超高压电力电缆关键技术分析及展望[J].高电压技术，2014，40（9）：2593-2612.

[11]杨春宇.电力电缆故障分析与诊断技术的研究[D].大连：大连理工大学，2013.

[12]袁燕岭，李世松，董杰，等.一种用磁传感器测量三芯对称电缆相电流的新方法[J].中国测试，2016，42（8）：29-32.

（编辑：刘杨）

An analytical method for calculating the surface magnetic field for three-core electrical power cables

LI Shisong1，YUAN Yanling2，DONG Jie2，GAN Jingfu2，HUANG Songling1，ZHAO Wei1
（1.Department of Electrical Engineering，Tsinghua University，Beijing 100084，China；2.Tangshan Electrical Power Company，Tangshan 063000，China）

Since the sum currents of three phases in the three-core cable is zero in steady state，traditional inductive current measurement methods， a current transformer， cannot measure the phase current.In order to solve this problem，this paper developed an analytical method for calculating the magnetic field on the surface of a three-core cable based on Maxwell equations which can be used for the generalized core contribution case rather than a symmetrical condition.Based on this analytical method，the phase current of the three-core cable can be represented by measurements of the magnetic field on the cable surface.The finite element simulations show that the presented analytical method has a good accuracy，and can be employed in future to realize an online power cable monitoring system.

electrical power cable；magnetic field calculation；analytical model；current measurement

A

1674-5124（2017）04-0095-05

10.11857/j.issn.1674-5124.2017.04.020

2016-10-13；

2016-11-19

李世松（1987-），男，山东昌乐县人，主要从事现代电磁测量和电磁计量方法研究。