时间序列数据中的干预分析模型及SAS实现

薛芳静 黄 灏 许碧云 张慧敏 陈炳为△



·计算机应用·

时间序列数据中的干预分析模型及SAS实现

薛芳静1黄 灏1许碧云2张慧敏1陈炳为1△

目的 利用干预分析模型从定量分析的角度来评估政策干预或突发事件对时间序列数据的具体影响。方法 本文以2010年1月至2013年5月某医院ICU抗生素多重耐药性的时间序列为例进行干预性分析。利用SAS中的PROC ARIMA程序可定量分析政策法规对抗生素多重耐药性的影响。结果 多重耐药性的干预分析模型中趋势估计参数为-0.00174，抗生素多重耐药性呈下降趋势，干预的MA系数为-0.662，干预变量系数为-0.117，说明限制抗生素使用的政策法规降低了医院抗生素使用量，使抗生素多重耐药性下降11.04%。结论 干预分析模型可以较好地处理“突变性”的时间序列问题，SAS中的PROC ARIMA程序为该模型提供了一种极为方便的实现形式。

干预分析模型 时间序列 抗生素

时间序列预测方法是以惯性原理推测其未来的状态，常见的有指数平滑法、ARIMA方法等[1]。但这些方法不能解决“突变性”的时间序列，如政策的实施或干预，这必将对事件发展过程产生影响，甚至改变事件发展结果。Box和Tiao于1975年提出干预分析模型(intervention analysis model)，较好地解决了这种“突变性”的时间序列。其被广泛用于经济政策的变化或突发事件对经济环境、经济过程或结果的具体影响的定量分析[2-3]。干预分析模型是将干预事件和时间序列模型结合起来进行研究的，它较好地解决了政策的变化或突发事件的影响及影响程度。如Bordet等在德国一家社区医院实施抗生素管理计划后利用干预分析模型得到该医院头孢菌素使用下降了33%，氟喹诺酮类使用下降了31%，证实在干预后头孢菌素类和氟喹诺酮类药物的使用密度趋势有显著的变化，抗生素总使用降低了11%[4]。

由于受到我国开始正式实施《抗菌药物临床应用管理办法》的影响，ICU的抗生素多重耐药性在干预前后发生了变化。本文利用SAS中的ARIMA过程，应用干预分析模型对某医院ICU的抗生素多重耐药性进行分析，以期得到干预前后抗生素多重耐药性的变化情况。

原理与SAS程序

1.干预变量

干预分析模型是在常规时间序列中加入干预变量，干预变量有两种形式[3,5]：一种是持续性的干预变量，即在T时刻发生后一直有影响，这时可以用阶跃函数表示：

第二种是短暂性的干预变量，即在事件发生时刻T有影响，用单位脉冲函数表示：

2.干预事件的形式

对于干预时间序列模型，干预事件按其影响有四种最基本的形式。其他的干预模型，不管是否受到多种干预，也不管这些干预影响有多复杂，都可用这四种形式组合表达[3,5]：

(1)干预事件的影响突然开始并持续

设干预事件在T时刻突然开始，干预对因变量的影响是固定且未知的。这时干预模型可写为：

其中ω表示干预影响程度的未知参数，B为后移算子。当Xt不平稳时，通过差分使序列成为平稳序列；当Xt平稳时，则不需差分。Bb是代表干预事件在b个时期(b=1,2,…)滞后才产生影响。

(2)干预事件的影响逐渐增大且持续

干预事件在T时刻突然发生，但其影响不是立刻全部产生，而是随着时间逐渐增大，这时模型可用下式表达：

(3)干预事件的影响突然开始且暂时性

这类干预现象可以用数学模型描述如下：

当δ=0时，干预的影响只存在一个时期，当δ=1时，干预的影响将长期存在。

(4)干预事件的影响逐渐增大后衰减

干预事件在T时刻突然发生，其影响逐渐增加，在某个时刻到达峰值，然后又逐渐减弱甚至消失，模型可表达为：

3.干预分析模型的构造与干预效应的识别

(1)模型的构造

干预模型主要是为了度量干预效应，剔除了干预影响后的序列可看作普通的序列，进而可以用一般的时间序列分析方法进行拟合。本文以Box-Jenkins的ARIMA模型进行干预模型的构造。

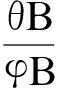
(2)干预效应的识别

根据序列的具体情况和干预变量的性质进行识别。利用干预变量产生影响之前或干预影响之后的净化数据计算出自相关函数与偏自相关函数。首先识别ARIMA模型中的p和q，然后估计出θB、φB中的参数。

(3)模型的判断

模型的拟合采用AIC统计量进行评价，依据AIC最小原则，选出最优ARIMA模型。加入干预变量后通过比较模型参数的t值和P值评价最终模型。

4.SAS软件的实现

本文利用SAS9.3的ARIMA过程步来实现，具体程序如下：

(1)ARIMA模型的识别

建立数据集

data a;

input y @@;

format date monyy.;

date=INTNX(′month′,′01JAN10′d,_N_-1);

x=(date>=′01JUN11′d);

proc gplot data=a;

symbol1 i=spline v=dot c=red;

plot y*date=1;

在DATA步利用INTNX函数生成时间序列，并生成阶梯函数X，利用GPLOT作出序列图。再利用ARIMA过程的identify语句对模型进行初步识别，观察样本自相关系数、偏相关系数及是否具有周期性等问题。

proc arima data=a;

identify var=y(1);

estimate q=(1)method=uls plot;

forecast lead=12 out=b id=date interval=month id=date;

run;

在ARIMA(p,d,q)模型拟合中，identify语句后的y(1)代表进行一阶差分，estimateq=(1)考虑模型中q=1的模型，即此时模型为ARIMA(0,1,1)，同时分别考虑ARIMA(1,1,0)、ARIMA(1,1,1)，从三种模型中选出最优模型。Forecast语句是按月份进行12个月的预测。完成上述三个模型结果，选取AIC最小的模型进行白噪声检验，同时可利用gplot程序作残差序列图，观察残差的特性。

(2)干预变量

proc arima data=a;

identify var=y(1)cross=(x(1));

estimate p=(1)q=(1)input=(x)method=cls;

forecast lead=12 out=a id=date interval=month;

run;

在identify语句中利用cross选项指定协变量x，在estimate利用input语句指定ARIMA模型中加入干预x，input后的变量一定要利用identify语句中的cross选项事先指定。

实例分析

据WHO资料显示，我国门诊感冒患者抗生率使用率为75%、外科手术高达95%、住院患者80%，其中使用广谱抗生素和联合应用的患者占58%，远高于国际上规定的抗生素使用率不超过30%的标准，而且我国每年有8万多人直接或间接死于滥用抗生素，由此造成的机体损伤及病原菌耐药性更是无法估量[6]。滥用抗生素将会使人类为对抗疾病付出越来越高的代价。2012年8月1日，我国正式开始实施《抗菌药物临床应用管理办法》，对抗生素临床使用做了严格规定，此办法的实施必然对我国抗生素的临床使用量产生影响。本文利用干预分析模型对2010年1月至2013年5月某医院ICU的抗生素多重耐药性进行干预前后间的差别分析，干预后的数据从2011年7月到2013年5月，数据见表1。使用上述SAS程序进行分析，首先绘制序列图(图1)，观察到该医院抗生素的多重耐药性从实施干预时开始减少。

随之采用自相关图检验法来检验平稳性，图2是样本自相关系数散点图，自相关系数缓慢趋于零，表明抗生素多重耐药性序列是非平稳的。因为序列是非平稳的，采用一阶差分进行平稳化处理。再次考察自相关系数图，处理后的数据满足平稳性，同时通过白噪声检验，可以进行ARIMA建模。用ARIMA(1,1,0)、ARIMA(1,1,1)、ARIMA(0,1,1)三种模型来进行拟合。

表1 2010年1月至2013年5月某医院ICU的抗生素多重耐药性

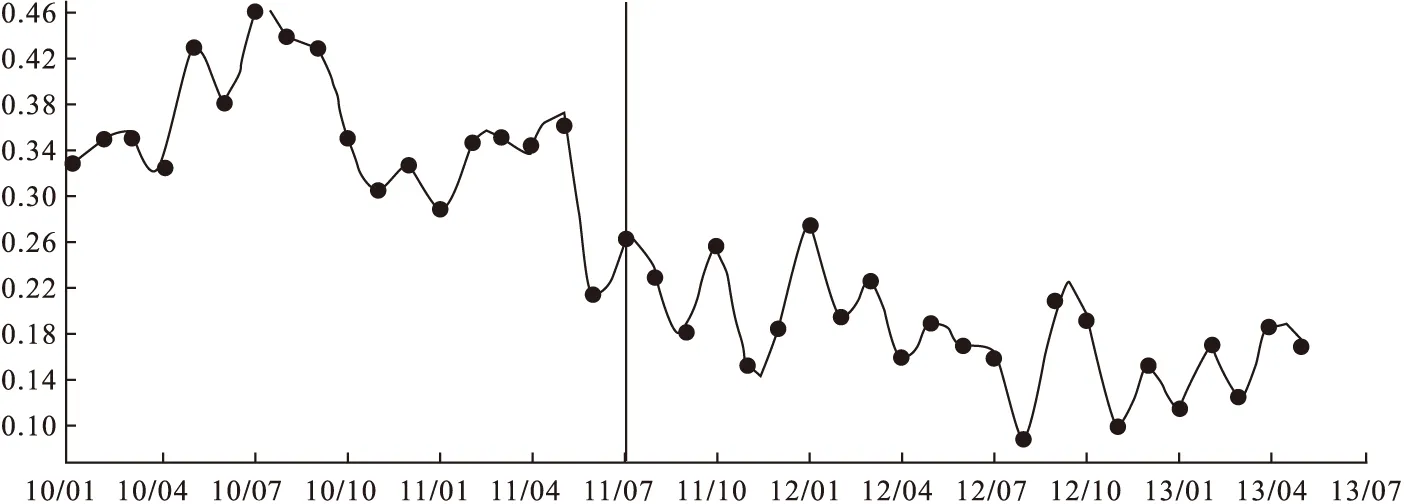
图1 某医院2010年1月至2013年5月ICU的抗生素多重耐药性时间序列图

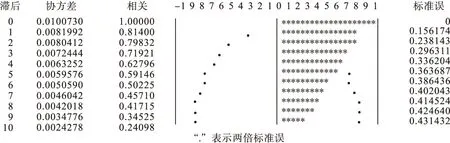
图2 样本自相关系数散点图

模型ARIMA(1,1,0)ARIMA(1,1,1)ARIMA(0,1,1)AIC-125.632-125.029-126.977

表2分别列出了模型的拟合情况。根据AIC最小准则，ARIMA(0,1,1)为最优模型。加入干预变量进行分析，结果见表3。

表3 加入干预变量后的ARIMA模型参数检验结果

多重耐药性的干预分析模型方程为Yt=-0.00174-0.117It+(1-0.662B)at，μ=-0.00174表明多重耐药性呈下降趋势，其下降量为1-e-0.00174=1.70%；干预的MA模型系数为-0.662，P<0.0001；干预变量的系数为-0.117，P=0.0046，说明限制抗生素使用的政策法规降低了医院抗生素多重耐药性，进而使抗生素多重耐药性下降了1-e-0.117=11.04%。

讨 论

延误 ICU抗生素合理用药(对病原体使用敏感药物)与住院死亡率息息相关，抗生素用药史是延误用药的最重要危险因素之一，且抗生素用药时间延长也是危重症患者出现耐药菌感染的最重要诱发因素。因此，ICU临床医生必须权衡两个问题：一是抗生素用药需满足现在所救治患者的需求，二是兼顾 ICU其他患者可能暴露于该抗生素治疗患者诱发的耐药菌感染[7]。在ICU，临床医生常会遇到的棘手问题是使用抗生素治疗危重症严重感染患者的同时，又要尽量减少耐药菌的出现及其传播。

干预分析模型是时间序列分析模型的一种推广,如果不存在干预影响,这两种模型就没有什么差别。干预分析模型可以对具有“突变性”的时间序列进行模拟化处理，定量分析政策干预或突发事件对事件过程结果的具体影响。干预分析模型与其他模型相比，有两个优点[8]：(1)干预事件影响存在，那么对时间序列分析和预测不论是用ARIMA 模型还是MARIMA模型(多变量时间序列的ARIMA模型)其预测精度都比干预分析模型差，也就是干预分析模型更接近实际，分析的结果更为客观。(2)干预分析模型比回归分析模型中加入虚拟量要灵活得多，适应能力强一些，因为干预分析模型能对时间序列的动态特性进行合理的描述,甚至可以对未来的影响做出主观估计，把先验信息反映到模型中。

干预分析模型从其出现时起，主要应用于经济政策的变化或突发事件对经济环境、经济过程或结果的具体影响的定量分析，较少被引入医学领域的研究。SAS中的PROC ARIMA程序为该模型提供了一种极为方便的实现形式。

[1]王涛,苑新海,朱宗龙.ARIMA时间序列在乙肝发病预测中的应用.中国卫生统计,2014,31(4):646-647,650.

[2]Box G,Tiao GC.Intervention Analysis with Applications to Economic and Environmental Problems.Journal of the American Statistical Association,1975,70(349):70-79.

[3]徐国祥.统计预测和决策.第2版.2005:上海财经大学出版社,396.

[4]Borde JP,Litterst S,Ruhnke M,et al.Implementing an intensified antibiotic stewardship programme targeting cephalosporin and fluoroquinolone use in a 200-bed community hospital in Germany.Infection,2015,43(1):45-50.

[5]冯文权,蔡基栋.干预分析模型及其应用.武汉大学学报(自然科学版),1994,33(6):29-35.

[6]胡燕,白继庚,胡先明,等.我国抗生素滥用现状、原因及对策探讨.中国社会医学杂志,2013,30(2):128-130.

[7]Kollef MH,Micek ST.Rational Use of Antibiotics in the ICUBalancing Stewardship and Clinical Outcomes.JAMA,2014，321(14):1403-1404.

[8]冯文权.政策干预或突发事件影响的统计分析模型.统计与决策,1990，(6):8-11.

(责任编辑：刘 壮)

1.东南大学流行病与卫生统计学系(210009)

2.南京大学医学院附属鼓楼医院

△通信作者：陈炳为，E-mail:drchenbw@126.com