不同混杂结构条件下各倾向性评分方法的模拟比较研究*
2017-07-18复旦大学公共卫生学院生物统计学教研室和公共卫生安全教育部重点实验室200032
复旦大学公共卫生学院生物统计学教研室和公共卫生安全教育部重点实验室(200032)
孙 婷 秦国友 武振宇△ 赵耐青
不同混杂结构条件下各倾向性评分方法的模拟比较研究*
复旦大学公共卫生学院生物统计学教研室和公共卫生安全教育部重点实验室(200032)
孙 婷 秦国友 武振宇△赵耐青
目的 通过构建不同混杂结构的处理因素模型和结局模型、不同相关性的协变量,比较多种倾向性评分方法在结局模型为线性回归模型的情况下估计处理效应的优劣。方法 采用Monte Carlo模拟方法,通过构建四种由简单到复杂的不同结构的混杂模型,生成相应的数据集,再分别应用倾向性评分匹配、回归调整、加权以及分层的方法估计处理效应并进行比较。评价指标包括点估计、标准误、相对偏倚、均方误差。结果 在结局模型为线性回归模型情况下,倾向性评分回归调整法估计的相对偏倚最小,稳定性也最好。匹配法卡钳值取0.02较卡钳值取倾向性评分标准差的0.2倍估计的相对偏倚更小。当处理因素模型中含有非线性效应时,用逆概率加权法估计的偏倚较大,并且加权法估计的标准误也最大。倾向性评分分层法在各种情况下估计的相对偏倚都较大。结论 倾向性评分回归调整法能够较好地估计处理效应,并且在各种情况下估计都较为稳健。建议当协变量与处理因素和结局变量的关系无法确定时,这四种方法中可以考虑优先使用回归调整法。
倾向性评分 混杂因素 Monte Carlo模拟 偏倚
随机对照试验(randomized controlled trial,RCT)被认为是评价干预作用设计的金标准,但由于RCT其自身的限制,在很多情况下无法实施[1]。而观察性研究或回顾性电子医疗病历的数据相对较易获得,因此越来越多地被应用于不同干预效果的比较、食品和药物安全研究、药物不良反应监测等。在观察性研究中,受试对象的治疗分组往往不是随机分配的,因此会存在某些重要混杂因素在不同组间分布不均衡,从而无法准确评价干预因素对结局的作用[2]。在不同调整混杂的方法中,由Rosenbaum和Rubin提出的倾向性评分(propensity score,PS)方法逐渐受到重视[3],倾向性评分是指在给定一组协变量的情况下,任意一个研究对象被分到处理组的条件概率,计算PS时不存在未观察到的混杂因素的假设条件下,基于PS的匹配法、分层法、回归调整法均能得到处理效应的相合估计[3]。
目前倾向性评分主要有倾向性评分匹配法、回归调整法、分层法和加权法四种应用方式。有文献总结了2001-2009年高影响力的医学和公共卫生杂志中使用倾向性评分的文献情况,其中匹配法是使用最多的方法,占所有查阅文献的三分之一,其次是回归调整法,约占24%,分层法和加权法分别占22%和18%[4]。评价各种倾向性评分方法估计效果的文献有很多,我们可以看到在估计不同指标的情况下各种估计方法的优劣有所不同[5-9]。在线性回归模型情况下,有文献指出PS回归调整法可以得出相合估计[10]。另外,当结局变量为连续性变量时,基于不同组别的倾向性评分重叠情况,几种不同的PS方法估计的优劣情况也不同[4],当处理组倾向性评分分布被包含在对照组中时,匹配法估计偏倚较小,但如果处理组和对照组倾向性评分分布重叠很小时,回归调整法表现更好。在医学研究中,有很多情况下结局为连续性变量,并且协变量之间存在不同情况的相关性,当协变量与处理因素和结局变量之间的混杂结构不同时,例如协变量与处理因素或结局变量之间不仅含有线性关系,还有非线性关系时,这四种基于PS的方法估计处理效应的偏倚大小和稳定情况还没有明确的结论。因此,本研究通过设置不同混杂结构的模型,在连续性结局变量、不同相关程度自变量的情况下,比较各种倾向性评分方法估计真实处理效应优劣的情况,为不同条件下观察性数据的分析处理提供依据。
原理与方法
倾向性评分是指在给定一组协变量(Xi)条件下,将任意一个研究对象i(i=1,2,…,n)分配到处理组(Zi=1)的条件概率。第i个研究对象被分配到处理组的条件概率可以表示为:
e(Xi)=P(Zi=1|Xi)
(1)
其中,e(Xi)被称为倾向性评分。倾向性评分相同的两个不同组别的研究对象,其拥有的多个协变量整体上分布是相同的[11]。因此,组间协变量的不均衡性对处理效应估计的干扰被消除了。
倾向性评分的基本原理是用一个分值来替代多个协变量,均衡处理组和对照组间协变量的分布。对非随机化研究中的混杂因素进行类似随机化的均衡处理,减少选择偏倚。计算得出PS分值后,可采用匹配、回归调整、加权、分层的方法来均衡各组间协变量的差异,最终估计处理效应。
1.倾向性评分匹配法
倾向性评分匹配是从对照组中选出与处理组中某一个体倾向性评分值相同或相近的个体进行配对,常用的匹配方法有最邻近匹配、卡钳匹配、全局最优匹配等。本研究采用的是最邻近卡钳匹配法,即将处理组和对照组的研究对象分别进行随机排序,然后从处理组中依次选出一个研究对象,从对照组中选出与其最接近的倾向性评分值的研究对象进行匹配。配对时设置两组倾向性评分的差值在一定范围内,即卡钳值(caliper)。根据以往研究建议[12],本研究设置两种卡钳值,分别为0.02和两组倾向性评分标准差的0.2倍。在匹配的过程中一个关键的问题是是否允许放回。有无放回是指配对后的对照组对象是否参加下一组的配对。允许放回在方差估计的过程中需要考虑某一研究对象被多次使用的事实[13]。本研究统一采用无放回匹配。
2.倾向性评分回归调整法
在四种基于倾向性评分的方法中,回归调整法是最直接、使用最为方便的一种方法,因此在临床医学研究中使用也较为广泛[4]。倾向性评分回归调整法是指将估计的倾向性评分值作为一个协变量与处理因素一起纳入到估计处理效应的回归模型中。对于本研究中连续性的结局变量使用线性回归方法,处理效应的估计是调整的均值差。尽管在某些条件下使用PS方法可以得到相应估计,但是当结局变量和PS值之间的线性关系不成立时,用这种方法估计的处理效应可能是有偏的[4]。
3.倾向性评分逆概率加权法(Inverse probability of weighting,IPW)
倾向性评分逆概率加权,是边缘结构模型这类因果推断方法中的一种[14],其基本原理与传统的标准化法类似。根据倾向性评分值赋予每个研究对象一个相应的权重,从而构建出一个虚拟的人群,在这个虚拟人群中,协变量的组间分布没有差异,因此消除了混杂因素的影响。在逆概率加权的方法中,权重被定义为研究对象实际分组情况的概率的倒数,计算如下:
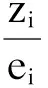
(2)
计算权重后,再应用加权回归的方法估计处理效应。
4.倾向性评分分层法(PS stratification)
分层法是非随机化研究中控制偏倚的重要手段。倾向性评分分层法是指在估计出每个研究对象的倾向性评分值后,根据倾向性评分值将研究对象分为若干层。文献指出,当估计线性处理效应的时候,将倾向性评分值分为五层可以消除组间近90%的混杂偏倚[15]。经过分层后,每一层内处理组与对照组的协变量分布应该是均衡的。分析过程中,先在每一层内估计处理效应,最后将每层的效应整合成总的处理效应。
模拟实验
在之前研究的基础上[16],本研究构建了四种由简单到复杂,不同结构的混杂模型,并且考虑协变量之间不同的相关性,分别使用倾向性评分回归调整、匹配、加权以及分层的方法估计处理效应并通过Monte Carlo模拟方法进行比较。
1.数据集生成和参数设置
(1)生成自变量
本研究共模拟20个协变量,其中X1~X10设置为混杂因素,这10个协变量的产生我们设置了三种不同的情形:
情形I:X1~X5为服从N(0,1)标准正态分布的连续性变量,并且自变量之间相互独立;X6~X10为服从Bern(0.5)分布的二分类变量,且相互独立。
情形II:X1~X5为服从N(0,1)标准正态分布的连续性变量,X1和X2具有相关性,相关系数R12=0.2;X6~X10为服从Bern(0.5)分布的二分类变量,且相互独立。
情形III:X1~X5为服从N(0,1)标准正态分布的连续性变量,X1和X2、X1和X3、X2和X4分别具有相关性,相关系数分别为R12=0.2,R13=0.3,R24=0.4;X6~X10为服从Bern(0.5)分布的二分类变量,且相互独立。
为了模拟实际情况,又生成另外10个相互独立的噪声协变量(X11~X20),与处理因素和结局变量均无关。其中X11~X15为服从N(0,1)标准正态分布的连续性变量,X16~X20为服从Bern(0.5)分布的二分类变量。
(2)生成处理因素和结局变量
为了模拟不同复杂程度的结构,我们设置了四种混杂模型来生成处理因素和结局变量。其中,简单混杂结构中只有线性关系,而复杂混杂结构分别是处理因素模型中含有非线性关系、结局变量模型中含有非线性关系以及两个模型中均含有非线性关系。
简单混杂结构:在这种简单线性情况下,处理因素由公式(3)产生,结局变量由线性回归模型公式(4)产生。其中α、β系数的值均从Unif(-1,1)中随机产生,并且在之后的模拟中固定,αZ为处理因素效应,设为0.5,i~N(0,1)代表随机测量误差。
logit{ei(Xi;θ1)}=β0+β1X1,i+…+β10X10,i
(3)
yi=αzZi+α1X1,i+…+α10X10,i+i,(i=1,…,n)
(4)
复杂混杂结构I:保持公式(4)不变,但处理因素改为由公式(5)生成。在这种情况下,X2和处理因素不仅存在线性关系,还存在二次项关系。
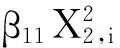
(5)
复杂混杂结构II:保持公式(3)不变,但结局变量由公式(6)生成。在这种情况下,X1与结局变量之间的关系是非线性的。

(6)
复杂混杂结构III:处理因素由公式(5)生成,结局变量由公式(6)生成。在这种情况下,处理因素模型与结局变量模型中均含有非线性关系。
按上述组合,分别生成了样本量为500和2000的数据集。因为实际情况中我们很难准确判断协变量因素与处理因素之间的关系,所以在估计倾向性评分值的过程中,我们将按照通常分析此类数据的做法,线性纳入所有20个协变量,再利用倾向性评分匹配法(两种卡钳值)、回归调整法、逆概率加权法、分层法分别估计处理效应。各种情况下分别重复模拟1000次。
2.评价指标
本研究评价指标包括处理效应的点估计(Average(αZ))及其标准误(SE(αZ))、相对偏倚(RB)、均方误差(MSE)。相对偏倚(RB)是点估计与真实效应之差的绝对值占真实效应的百分比,均方误差为偏倚的平方与标准误平方之和。
3.软件实现
本研究采用R 3.2.3软件进行模拟实验。其中倾向性评分匹配法使用R软件中的MatchIt包实现。下面这段程序可以分别实现本研究中的几种倾向性评分方法:
#估计倾向性评分值
>psfit=glm(treat~x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20,data,family=binomial())
>ps=fitted(psfit)
#倾向性评分回归调整法
>yfit=lm(outcome~treat+ps,data)
>cov.est=coef(summary(yfit))[2,1]
#倾向性评分逆概率加权法
>dataf$wgt=treat/ps+(1-treat)/(1-ps)
>iptw.fit=lm(outcome~treat,data,weights=wgt)
>iptw.est=coef(summary(iptw.fit))[2,1]
#倾向性评分分层法
>quintiles=quantile(data$ps,prob=seq(from=0,to=1,by=0.2),na.rm=T)
>data$pstrata=cut(data$ps,breaks=quintiles,labels=1:5,include.lowest=T)
>stratified=dlply(.data=data,.variables=“pstrata”,.fun=function(DF){lm(outcome~treat,data=DF)})
>sub.est=mean(sapply(stratified,function(mod)mod$coef[“treat”]))
#倾向性评分匹配法
>psmatch=matchit(treat~x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20,distance=“logit”,caliper=0.2,method=“nearest”,data)
>psmatch.data=match.data(psmatch)
>match.fit=lm(outcome~treat,data=psmatch.data)
>match.est=coef(summary(match.fit))[2,1]
4.模拟实验结果
从表1可见,当样本量为500且自变量之间相互独立时,倾向性评分回归调整法在四种不同的方法中估计效果最好,相对偏倚范围在0.17%~0.50%,并且随着模型复杂度的增加,即模型中含有二次项时,这种优势保持不变。匹配法设置了两种卡钳值,其中匹配法-1代表卡钳值为两组倾向性评分标准差的0.2倍,匹配法-2代表卡钳值为0.02。由结果可见,当卡钳值设为0.02时,匹配法估计的较为准确,相对偏倚在2.86%~7.55%,在混杂结构最为复杂的情况下,即处理模型和结局模型均含有二次项时,相对偏倚达到最大(7.55%)。而匹配法-1估计的准确性则较差,相对偏倚均在10%以上,并且随着混杂结构复杂性的增加,相对偏倚也逐渐增加。加权法在仅处理模型中含有非线性关系的情况下,估计情况较差,相对偏倚达到14.73%,在另外三种情况下偏倚相对较小,均保持在10%以内。分层法在各种情况下估计的偏倚较大,其中在复杂混杂结构II情况下偏倚达到了19.78%。在估计的稳定性上,回归调整法也较其他三种方法好,均方误差最小,而加权法标准误和均方误差最大。
当增加了X1与X2之间的相关性,结果见表2,当处理因素模型和结局变量模型中均含有非线性关系时,回归调整法的估计稍有偏倚,相对偏倚为3.58%,其余情况下,回归调整方法仍估计准确,相对偏倚范围为0.31%~0.46%,稳定性也较其他方法好,均方误差最小。匹配法-2在简单混杂结构下,偏倚相对较小,而只要有一个模型中含有非线性关系时,相对偏倚增大,在复杂混杂结构III情况下,相对偏倚达到11.39%。与表1结果相似,匹配法-1估计的偏倚依然较大。仅处理因素模型中含有非线性关系时,逆概率加权法估计的相对偏倚达到13.6%,在其他三种情况下,相对偏倚都较小,但标准误和均方误差在四种方法中为最大。分层法估计的准确性仍旧较差,相对偏倚大部分都在10%以上,标准误相对较小。继续增加自变量之间的相关性,结果见表3,回归调整法在准确性和稳定性方面,表现均最好。匹配法-1估计的相对偏倚随着自变量之间相关性的增加而增大,匹配法-2在简单混杂结构情况下,估计也较前两种情况准确性差。总体来看,随着协变量之间相关性的增加,这四种方法的估计的准确性和稳定性优劣模式差异不大。
当样本量增加(n=2000),回归调整法估计较为准确,匹配法-2表现较匹配法-1好,估计更为准确。加权法在处理因素模型中不含有二次项的情况下估计效果较好,相对偏倚都在1%以下。当处理因素与协变量之间含有非线性关系时,即在复杂混杂结构I和III两种情况下,加权法估计偏倚较大,而且后者相对偏倚较前者小。分层法在样本量增加后估计结果仍不准确。在稳定性上,随着样本量增加,各种方法的标准误和均方误差均减小,回归调整法的标准误最小,均方误差也最小,加权法估计的标准误最大。

表1 不同模型情况下各种倾向性评分方法的估计结果(自变量之间独立)
讨 论
倾向性评分方法作为控制混杂的分析方法在医学研究中应用越来越广泛。本研究的主要目的是在不同混杂结构情况下,比较倾向性评分匹配法、回归调整法、逆概率加权法以及分层法对处理效应的估计优劣。Austin在多篇文献中也比较过这几种倾向性评分方法[7-11],但本研究内容和他之前的文献有所不同。在本研究中我们设置了不同的生成处理因素的模型和结局变量模型,通过加入协变量与处理因素和结局变量的非线性关系逐步增加混杂结构的复杂性,根据文献检索,还没有这方面深入的探讨。另外,还模拟了协变量之间存在相关性的各种不同情况,更加贴近了实际。
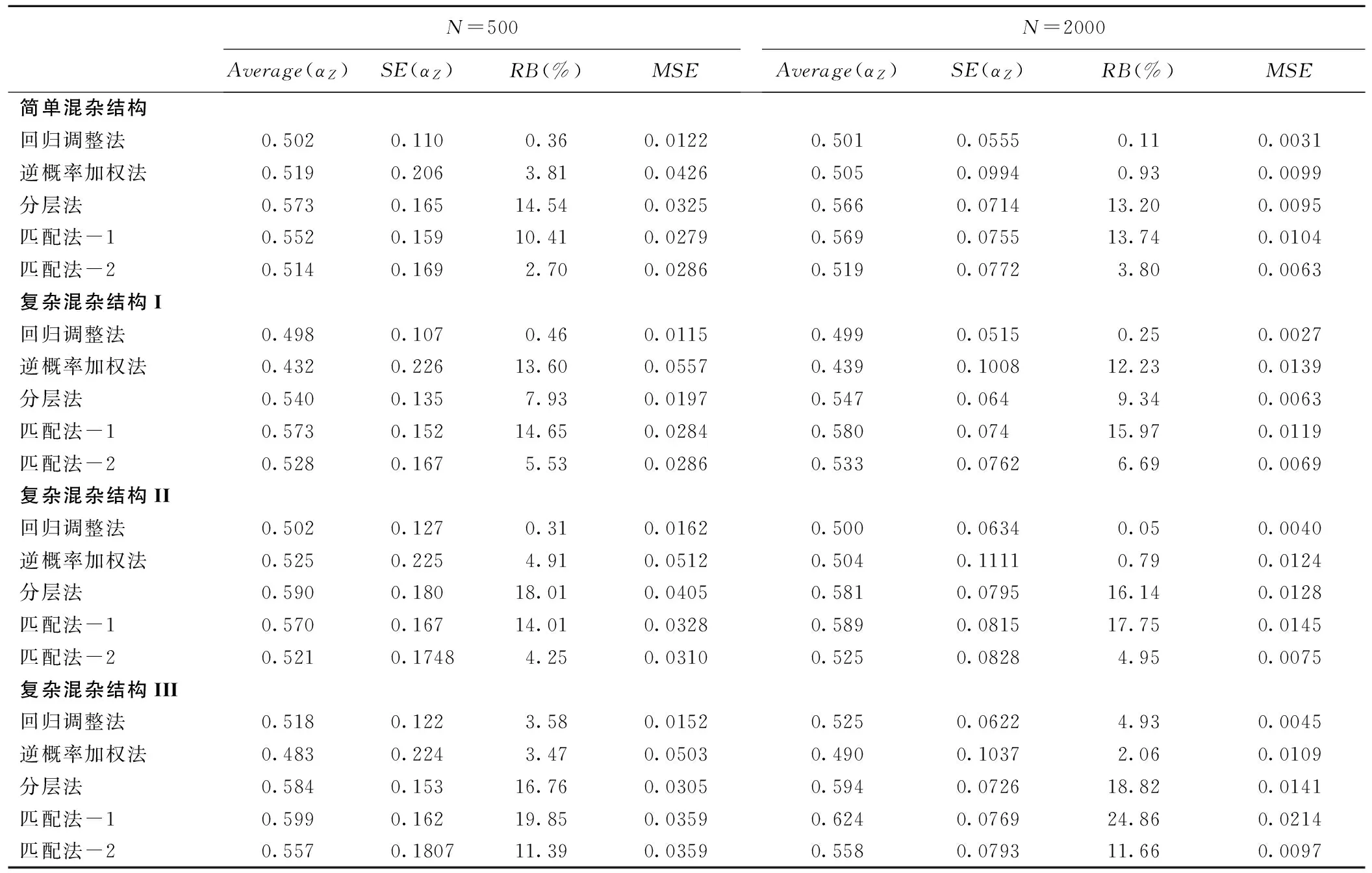
表2 不同模型情况下各种倾向性评分方法的估计结果(R12=0.2)
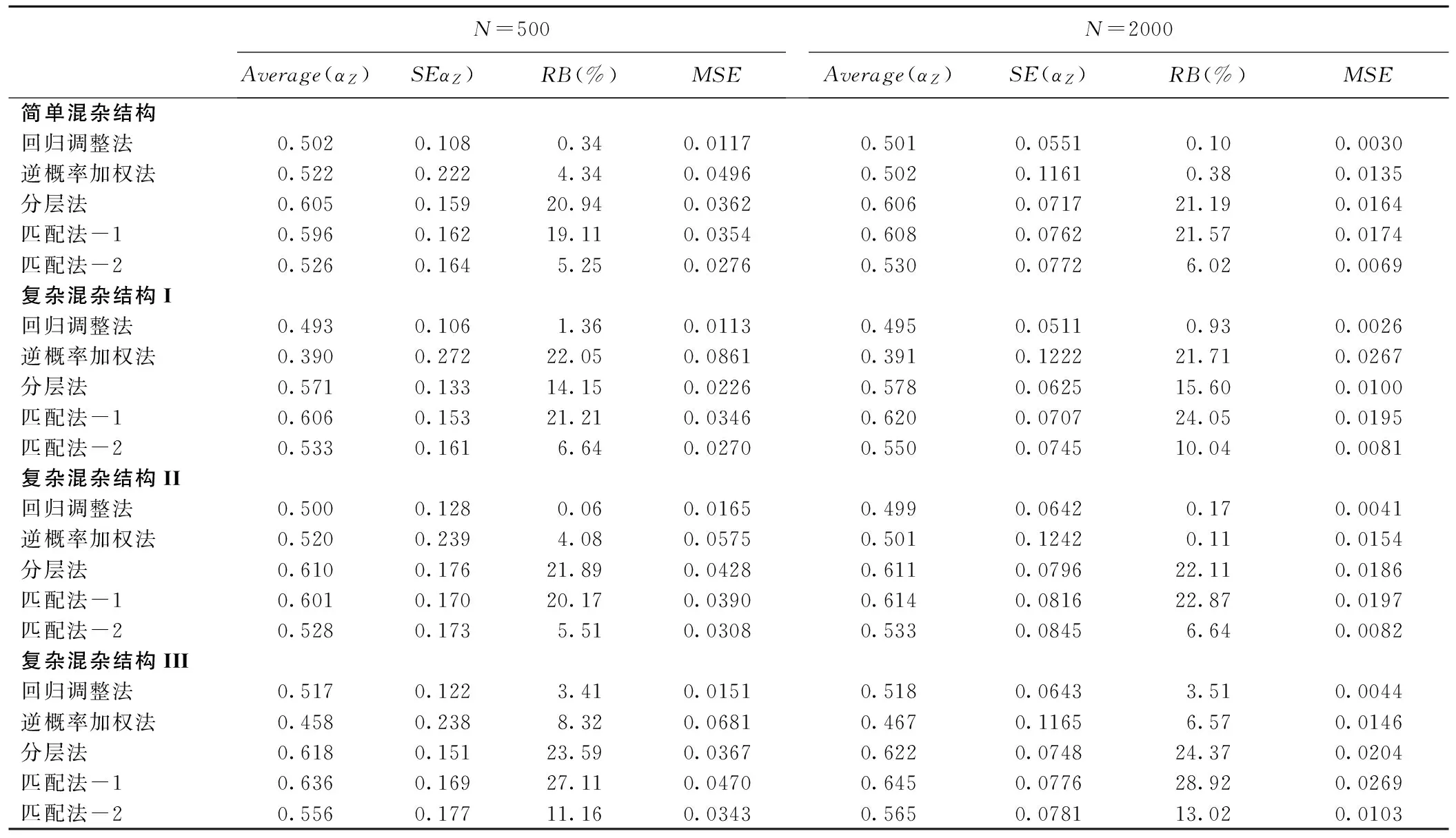
表3 不同模型情况下各种倾向性评分方法的估计结果(R12=0.2,R13=0.3,R24=0.4)
倾向性评分回归调整法在不同的情况下估计的相对偏倚较分层法和加权法都小,并且MSE最小,这与Austin得出的结论也相同[7]。由模拟结果可见,通过设置不同的卡钳值,估计的结果相差较大。卡钳值设为0.02比卡钳值设为倾向性评分标准差的0.2倍准确性好。倾向性评分匹配法是医学文献中应用较多的调整混杂的方法,而卡钳值的选择对结果的估计有很大的影响。本研究采用以往文献中建议的两种卡钳取值分别进行匹配估计,得出的结果相差很大,因此在应用卡钳匹配方法的过程中,卡钳值应当根据实际匹配后组间均衡性来考虑,对于不同的数据集情况下,以往研究建议的参数需要慎重选择。
当处理因素模型中不含有二次项时,即在简单混杂结构和复杂混杂结构II这两种情况下,倾向性评分加权法估计效果较好,并且随着样本量的增加,估计结果更为准确,均方误差也减小。Austin也在文献中提到,应用倾向性评分逆概率加权法可以得到风险差(risk difference,RD)的相合估计[9]。但在复杂混杂结构I、III情况下加权法估计的准确性又较差。在这两种情况下,真实的处理因素模型含有非线性关系,而估计倾向性评分的过程中只纳入了线性关系,因此计算的权重有误,从而导致估计的处理效应偏差较大。Linder等在文献中得出类似结论[17],即使结局模型指定错误,基于PS的逆概率加权方法也可以得出相合估计,而当PS模型指定错误时,基于PS的逆概率加权方法估计结果较差。模拟结果中,分层法估计的相对偏倚在各种情况下均较大,而这也是分层法的一个缺陷,有文献显示其估计的偏倚较其他倾向性评分法更大[18]。
本研究模拟了协变量之间不同相关程度的情况,但在不同的相关性情况下,各种方法的估计优劣情况类似。倾向性评分是将多个协变量的影响综合成一个变量,起到一个“降维”的作用,这也是倾向性评分方法优于传统多元回归方法的一个优点,传统多元回归方法中可能需要考虑协变量之间的相关性、共线性问题,但我们的模拟结果显示在不同协变量相关性情况下使用倾向性评分方法估计的结果似乎差异不大。
总体来说,从估计的相对偏倚大小和稳定性方面考虑,我们认为倾向性评分回归调整法能够更好地估计处理效应,并且在我们设置的各种混杂情况下的估计都较为稳健,因此当协变量数目较多并且协变量与处理因素和结局变量的关系无法确定时,这四种方法中可以考虑优先使用回归调整法。本研究存在的局限性是未考虑结局变量是二分类、计数资料或生存资料的情况下,各种倾向性评分方法估计效果的优劣。此外,值得注意的是,倾向性评分方法一个前提假定就是所有的混杂因素都已经观察到,对于未观察到的重要混杂因素并不能进行均衡,因此在后续研究中可以进一步探索未包含重要混杂协变量时倾向性评分估计的准确性。
[1]Johnston SC,Rootenberg JD,Katrak S,et al.Effect of a US National Institutes of Health programme of clinical trials on public health and costs.Lancet,2006,367(9519):1319-1327.
[2]Sturmer T,Joshi M,Glynn RJ,et al.A review of the application of propensity score methods yielded increasing use,advantages in specific settings,but not substantially different estimates compared with conventional multivariable methods.J Clin Epidemiol,2006,59(5):437-447.
[3]Rosenbaum PR,Rubin DB.The central role of the propensity score in observational studies for causal effects.Biometrika,1983,70(1):41-55.
[4]Hade E M,Lu B.Bias associated with using the estimated propensity score as a regression covariate.Stat Med,2014,33(1):74-87.
[5]Austin PC.The performance of different propensity score methods for estimating marginal odds ratios.Stat Med,2007,26(16):3078-3094.
[6]Austin PC,Grootendorst P,Anderson GM.A comparison of the ability of different propensity score models to balance measured variables between treated and untreated subjects:a Monte Carlo study.Stat Med,2007,26(4):734-753.
[7]Austin PC.The performance of different propensity-score methods for estimating relative risks.J Clin Epidemiol,2008,61(6):537-545.
[8]Austin PC,Grootendorst P,Normand SL,et al.Conditioning on the propensity score can result in biased estimation of common measures of treatment effect:a Monte Carlo study.Stat Med,2007,26(4):754-768.
[9]Austin PC.The performance of different propensity-score methods for estimating differences in proportions(risk differences or absolute risk reductions)in observational studies.Stat Med,2010,29(20):2137-2148.
[10]Pfeiffer RM,Riedl R.On the use and misuse of scalar scores of confounders in design and analysis of observational studies.Stat Med,2015,34(18):2618-2635.
[11]Austin PC.An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies.Multivariate Behav Res,2011,46(3):399-424.
[12]Austin PC.Some methods of propensity-score matching had superior performance to others:results of an empirical investigation and Monte Carlo simulations.Biom J,2009,51(1):171-184.
[13]Hill J,Reiter JP.Interval estimation for treatment effects using propensity score matching.Stat Med,2006,25(13):2230-2256.
[14]Thoemmes FJ,Kim ES.A Systematic Review of Propensity Score Methods in the Social Sciences.Multivariate Behav Res,2011,46(1):90-118.
[15]Rosenbaum PR,Rubin DB.Reducing bias in observational studies using subclassification on the propensity score.Journal of the American Statistical Association,1984,79(387):516-524.
[16]Zou B,Zou F,Shuster JJ,et al.On variance estimate for covariate adjustment by propensity score analysis.Stat Med,2016,35(20):3537-3548.
[17]Linden A,Uysal SD,Ryan A,et al.Estimating causal effects for multivalued treatments:a comparison of approaches.Stat Med,2016,35(4):534-552.
[18]Austin PC.The performance of different propensity score methods for estimating marginal hazard ratios.Stat Med,2013,32(16):2837-2849.
(责任编辑:张 悦)
Comparison of Propensity Score Methods Under Different Confounding Structures:A Simulation Study
Sun Ting,Qin Guoyou,Wu Zhenyu,et al
(DepartmentofBiostatistics,SchoolofPublicHealthandKeyLaboratoryofPublicHealthSafety,MinistryofEducation,FudanUniversity(200032),Shanghai)
Objective The performance of propensity score(PS)methods were compared through constructing different confounding structures and generating covariates with different correlations when the outcome model was linear.Methods Monte Carlo method was used to simulate the datasets by constructing four confounding structures from simple to complex.Then four PS-based methods including PS matching,covariate adjustment,inverse probability of weighting(IPW)and stratification were applied to estimate the treatment effect.The results were compared from different aspects including the point estimate,standard error,relative bias and mean square error.Results When the outcome model was linear,covariate adjustment showed the least biased and stable estimates among the four methods.PS matching with caliper 0.02 performed better than the other matching methods when the caliper is 0.2 of the standard deviation of the PS value.When there were nonlinear relationship in the treatment model,IPW showed biased results and largest standard error.PS stratification resulted in biased estimates in all settings.Conclusion Covariate adjustment by PS is robust to complex confounding structure and achieved the least biased estimates.We propose that when the relationships between confounding factors and treatment or outcome variable cannot be confirmed,using PS covariate adjustment seems a better choice.
Propensity score;Confounding factor;Monte Carlo simulation;Bias
国家自然科学基金(编号:11371100);上海市科研计划项目(编号:13411950406)
△通信作者:武振宇,E-mail:zyw@fudan.edu.cn
