改进的GM(1,1)幂模型在出院人数预测中的应用*

2017-07-18刘雁灵曹文君

中国卫生统计 2017年3期

刘雁灵李菲曹文君

刘雁灵1李菲2曹文君3△

出院人数是医院医疗工作的重要组成部分，是衡量医院工作成果和工作效率的重要指标之一，对其进行科学的预测，可以为医院制定决策、编制工作计划提供依据，依此提高医院各方面的工作效率以满足患者的需求，从而提高医院的社会效益和经济效益[1-2]。本文以改进灰导数的GM(1,1)幂模型为基础，利用傅里叶级数对其残差进行修正，建立改进的GM(1,1)幂

模型，对我校附属医院的出院人数进行预测，以期达到满意的拟合和预测效果。

资料来源与方法

1.资料来源

本研究资料来源于我校附属医院信息科2006-2015年医院医疗质量统计报表，各年份出院人数见表1。

表1 我院2006-2015年出院人数

2.方法

本文以改进灰导数的GM(1,1)幂模型为基础，利用傅里叶级数对其残差进行修正，建立改进的GM(1,1)幂模型，对我院的出院人数进行拟合和预测。

(1)GM(1,1)幂模型

定义1[3]若设X(0)、X(1)、Z(1)如上所述，则称

x(0)(k)+az(1)(k)=b(z(1)(k))γ

(1)

为GM(1,1)幂模型。其中，γ≠1，-a为发展系数，b为灰色作用量。

定义2[3]称

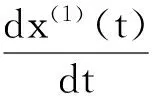
(2)

为GM(1,1)幂模型的白化微分方程。

采用文献[4]的方法得到幂指数γ的估计，再根据(1)式对参数(a,b)T作最小二乘估计：

(a,b)T=(BTB)-1BTY

(3)

其中

①白化微分方程的解也称时间响应函数为

②GM(1,1)幂模型的时间响应序列为

(5)

③还原值为

(6)

(2)改进灰导数的GM(1,1)幂模型

定义3[5]称

2x(0)(t+1)+a(x(1)(t)+x(1)(t+1))=b((x(1)(t))γ+(x(1)(t+1))γ)

(7)

为改进灰导数的GM(1,1)幂模型。

利用最小二乘法原理，得到(a,b)T的估计：

(a,b)T=(B1TB1)-1B1TY

(8)

(3)残差的修正[6]

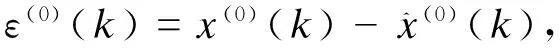
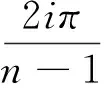
(9)

其中m=[(n-1)/2]-1，k=2,3,…,n。

通过最小二乘法原理推导出参数ai(i=0,1,…,m)和bj(j=1,2,…,m)的估计值：

(a0,a1,b1,…,am,bm)T=(PTP)-1PTE

(10)

其中

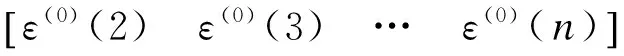
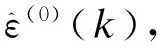
(11)

结果

1.建立GM(1,1)幂模型

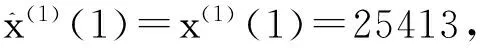
2.建立残差修正的GM(1,1)幂模型

3.建立改进灰导数的GM(1,1)幂模型

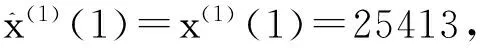
4.建立改进的GM(1,1)幂模型

由表2可以看出，改进的GM(1,1)幂模型所得各年份的相对误差介于0.0208%～3.1489%，且相对误差平均值为1.4382%，是四种方法最小者，说明各年份人数的拟合精度较高，另外，四种方法对2015年出院人数的预测值为46895.8287、45590.2754、46740.2629、45537.3868，相对误差为5.0934%、2.1677%、4.7448%、2.0491%，这也表明了改进的GM(1,1)幂模型的预测精度要高于其它三种方法。

表2 四种方法拟合结果的比较

讨论

灰色GM(1,1)幂模型是一种非线性灰色模型，适用于小样本震荡序列的预测[7]。由于受气候等因素的影响，出院人数是一个含不确定性信息的时间序列，且通过原始数据可发现，出院人数是一个单峰序列，故可采用灰色GM(1,1)幂模型对其进行拟合和预测。为了提高GM(1,1)幂模型的拟合精度，很多文献提出了改进措施[5-10]。本文以改进灰导数的GM(1,1)幂模型为基础，利用傅里叶级数修正残差的方法对我院出院人数进行了拟合和预测。通过四种方法结果的比较，得出本文方法具有较高的拟合和预测精度，故改进的GM(1,1)幂模型可用于出院人数的预测，并可将该法在医学或其它领域推广使用。

[1]关国琼，向德尚，胡传慧.我院出院人数预测模型分析.中国卫生统计，2011，28(6)：712-713.

[2]黄利娟，梁学柱，查君敬.应用自回归移动平均模型预测医院出院人数.中国病案，2014，15(9)：34-36.

[3]党耀国，王正新，钱吴永，等.灰色预测技术方法.北京：科学出版社，2014，83-86.

[4]王正新，党耀国，刘思峰.GM(1,1)幂模型求解方法及其解的性质.系统工程与电子技术，2009，31(10)：2380-2383.

[5]王丰效.改进灰导数的GM(1,1)幂模型.纯粹数学与应用数学，2011，27(2)：148-150，157.

[6]王正新.基于傅里叶级数的小样本振荡序列灰色预测方法.控制与决策，2014，29(2)：270-274.

[7]赵亚琴.傅里叶级数修正的灰色幂模型的小麦蚜虫量预测.统计与决策，2016，21(4)：78-80.

[8]王丰效.改进的GM(1,1)幂模型及其参数优化.纯粹数学与应用数学，2011，27(6)：711-714.

[9]王正新，党耀国，裴玲玲.灰色GM(1,1)幂模型初始条件的组合优化.统计与信息论坛，2012，27(6)：55-59.

[10]王正新，党耀国，赵洁珏.优化GM(1,1)幂模型及其应用.系统工程理论与实践，2012，32(9)：1973-1978.

(责任编辑：张悦)

国家自然科学基金项目(81302518)；山西省软科学研究计划项目(2016041035-3)；长治医学院博士科研启动基金项目(BS15016)