长沙市金属和类金属职业病危害因素检测超标率时间序列分析*

2017-07-18胡平成金若刚李继猛

中国卫生统计 2017年3期

何俊胡平成金若刚罗磊李继猛

何俊1胡平成2金若刚1罗磊1李继猛1

目的了解长沙市金属和类金属职业病危害因素检测超标率变化趋势，建立季节性ARIMA模型进行短期预测，为控制工作场所金属和类金属危害提供措施建议。方法利用2008-2015年检测数据为训练集进行建模，利用2016年上半年数据为验证集检验，并进一步预测2016-2017年的超标率。结果金属和类金属超标率长期趋势为逐年下降，且具有一定的季节效应，其中二、三季度较高，一、四季度较低。建立ARIMA(0,1,1)×(0,1,1)4模型，经检验残差为白噪声序列，预测的平均绝对误差(MAE)为4.54%。结论长沙市金属与类金属危害的控制近年来取得了一定的成效，超标率呈逐年下降趋势。2017年第二季度是金属与类金属危害控制的重点。季节性ARIMA模型在金属与类金属检测超标率预测方面有一定的可行性，今后可以和其他模型联合降低预测误差。

金属与类金属职业病危害因素超标率 ARIMA模型

长沙市工业企业以机械制造、金属加工、汽车制造、电气电子、化工等产业为主导，存在锰、铅、锡、锌、铜、镉、铬、磷、砷等多种金属和类金属职业病危害因素。劳动者在生产过程中可能因意外事故、燃烧或焊接吸入高浓度金属烟雾导致急性中毒，低剂量长时间接触金属和类金属也可引起慢性中毒[1]。预防和控制金属和类金属职业病危害因素对保护劳动者身体健康至关重要。

自回归滑动平均混合模型简称ARIMA模型，目前已在公共卫生领域得到广泛应用，如流感、结核、乙肝、猩红热、甲肝、呼吸道传染病、手足口病、梅毒的发病预测[2-9]，住院人数、门诊量、门诊收入变化趋势的季节调整等方面[10-12]，但在职业卫生领域的应用还鲜有报道。本文通过分析2008-2016年上半年长沙市工业企业金属和类金属职业病危害因素的检测结果，利用季度超标率建立季节性ARIMA模型，对未来金属和类金属危害的变化趋势进行预测，以制定降低工作场所有害物质浓度和保护劳动者健康的策略与措施。

资料与方法

1.资料来源

本研究资料来自2008-2016年上半年长沙市疾病预防控制中心依法对长沙市用人单位每年一次的定期检测，这里对用人单位的定义与《中华人民共和国职业病防治法》的阐述保持一致，即存在粉尘、放射性物质和其他有毒、有害因素的企业、事业单位和个体经济组织。长沙市疾病预防控制中心定期检测的用人单位主要来自职业卫生服务市场化前的主管企业，分布在全市各行业和地区，可基本代表长沙市存在职业病危害因素用人单位的危害状况。

2.分析方法

ARIMA模型是Box-Jenkins方法中成熟的时间序列分析预测方法，模型主要分析时间序列的随机性、平稳性和季节性，根据Akaike′s information Criterion(AIC)和Schwarz′s Bayesian Criterion(BIC)选择合适的参数进行预测，并通过Box-Ljung检验、平均绝对误差(MAE)、平均相对误差(MAPE)对模型进行评价。ARIMA建模主要包括三个内容：自回归、滑动平均、差分求和，季节性模型一般表示为ARIMA(p,d,q)×(P,D,Q)s，其中p、P表示模型的普通、季节自回归阶数，d、D分别表示普通、季节平稳化的差分阶数，q、Q表示普通、季节移动平均阶数[13]。模型公式为：

φ(B)=1-φ1B-φ2B2-…-φpBp

θ(B)=1+θ1B+θ2B2+…+θqBq

ΦP(Bs)=1-Φ1Bs-Φ2B2s-…-ΦPBPs

ΘQ(Bs)=1+Θ1Bs+Θ2B2s+…+ΘQBQs

▽d=(1-B)d

本研究采用excel 2016进行数据录入汇总，利用R(3.3.1)进行ARIMA建模、检验、预测和绘图。

结果

1.金属和类金属超标率序列特征

本研究数据为2008-2016年上半年金属和类金属检测数据，选择2008-2015年数据为训练集，2016年上半年数据为验证集进行建模。对训练集数据用stl函数进行分解，图1展现了原始序列、季节性、长期趋势、不规则变化四个部分，序列长期趋势明显，基本呈下降趋势，且具有一定的季节效应，高峰位于每年的第二、三季度，而第一、四季度较低。

图1 超标率时间序列分解图

2.季节性ARIMA模型的建立

(1)序列平稳化

金属和类金属超标率时间序列有明显的长期趋势，提示可能为非平稳序列，由于原始序列部分季度数据为0，为降低序列波动，采用加1后自然对数变换的方式进行统计变换。对新序列进行普通差分并绘制ACF(自相关系数)图和PACF(偏相关系数)图，其中ACF图显示序列存在一定的周期性，第1、5、9、13阶相关系数显著增大，对序列再进行季节性差分，经ADF单位根检验，统计量为-6.23，P=0.01<0.05，说明两次差分后的序列无单位根，为平稳序列，见图2。

(2)模型的识别与建立

图2两次差分后的序列仍存在一定的周期性，其中ACF图第1、5、13阶相关系数增大，可视为季节性1阶后截尾或拖尾，PACF图第1、4、5、8、9、12、13、16阶显著增大，可视为季节性1阶后截尾、3阶后截尾或拖尾，则P、Q有(0,1)、(1,0)、(1,1)、(3,0)、(3,1)五种可能。

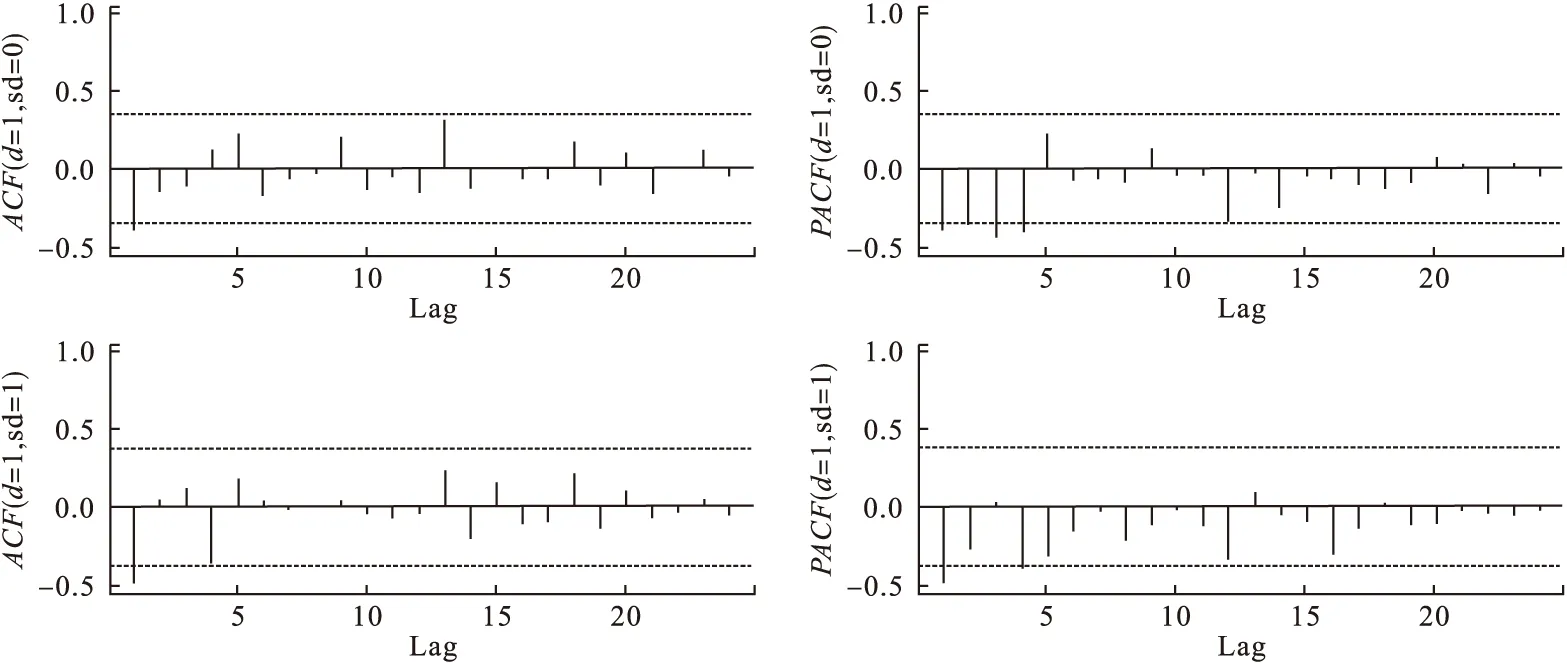
图2 两次差分的ACF图和PACF图

周期内ACF图可看做1阶后截尾或拖尾，PACF图可看做拖尾，则p、q有(0,1)、(1,1)两种可能。利用P、Q、p、q可能的参数组合分别建模，由于是差分序列，各模型均未包含常数项，计算得AIC和BIC值见表1。其中ARIMA(0,1,1)×(0,1,1)4的AIC和BIC值均最小，t检验表明模型参数不为零，ARIMA(0,1,1)×(0,1,1)4为最优模型，表达式为：(1-B4)(1-B)xt=(1-0.68B4)(1-0.95B)wt，各参数见表2。

表1 模型的AIC、BIC值

表2 ARUNA(0,1,1)×(0,1,1)4模型参数

(3)模型的诊断与验证

对ARIMA(0,1,1)×(0,1,1)4模型回归残差进行Ljung-Box检验，滞后3阶到16阶的自相关系数相应Ljung-Box检验统计量的概率值都大于0.05，可以认为模型序列不存在自相关，为白噪声序列，见图3。

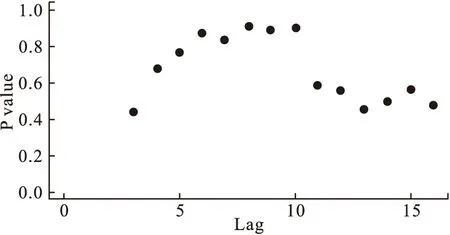
图3 Ljung-Box检验结果

为验证ARIMA(0,1,1)×(0,1,1)4模型的效果，利用模型对长沙市2016年第一、二季度金属类职业病危害因素检测超标率预测，预测结果分别为1.48%、4.89%，实际超标率为0、12.5%，所选模型的平均绝对误差(MAE)为4.54%。

(4)预测

将2016年上半年实际数据加入ARIMA(0,1,1)×(0,1,1)4重新建模，经Box-Ljung检验，3-16阶P值均大于0.05，残差为白噪声序列。利用新模型对2016-2017年长沙市金属类职业病危害因素检测超标率进行预测，6个季度超标率分别为2.63%、1.95%、0、5.89%、0.93%、0.26%，超标率峰值在第二季度，见图4。

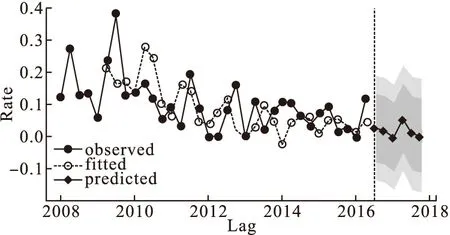
图4 长沙市金属类职业病危害因素检测超标率预测

讨论

金属和类金属是长沙市用人单位存在的主要职业病危害因素之一，控制其工作场所浓度和降低超标率是急慢性中毒类职业病防治的重中之重[15]。本研究采用季节性ARIMA模型对金属和类金属超标率历史数据进行了分析，对短期内超标率进行了预测，旨在发现近年来长沙市金属和类金属职业病危害变化的特点和规律，从而制定有力的控制措施。

时间序列的长期趋势显示检测超标率呈逐年下降趋势，表明长沙市职业病防治工作近年来取得了一定的成效。时间序列同时也存在一定的季节性，二、三季度较一、四季度有更高的超标率，一方面这可能与某些毒物在气温较高时容易挥发和扩散有关，另一方面长沙市疾病预防控中心检测行业的季度分布并不均匀，机械加工和电气电子等金属和类金属工艺较多的用人单位在二、三季度检测较多，从而导致金属类职业病危害超标率更高[15]。

本研究利用长沙市金属与类金属职业病危害因素的季度超标率建立ARIMA(0,1,1)×(0,1,1)4模型，对未来超标率进行了短期预测。模型2016年上半年超标率的验证表明预测值与实际值的发展趋势一致，通过诊断和检验说明该模型对长沙市金属与类金属超标率的预测具有一定的可行性，但2016年第二季度还存在较大预测误差，在以后的研究中可试验ARIMA与其他模型联合提高预测能力。

长沙市金属与类金属类职业病危害因素有较明显的时间趋势和季节趋势，根据序列的规律对未来超标率进行预测，可预先了解金属与类金属类职业病危害情况的发展状况，以提前发现高风险企业，采取适当的控制措施降低金属与类金属对劳动者身体健康的损害。预测显示2017年第二季度金属与类金属的危害较大，提示我们在工作中尤其要关注此时期内检测企业的金属与类金属危害，发现问题需及时向安全生产监管等政府部门进行反馈，密切注意工作场所金属与类金属浓度的变化，从而防患于未然，降低职业性急性金属与类金属中毒的发病率。模型以历史超标率数据建立，在今后的预测中还需加入每年的新数据进行修正，提高金属与类金属超标率预测的准确性[9]。

[1]孙贵范.职业卫生与职业医学.第7版.北京:人民卫生出版社,2012.

[2]Song X,Xiao J,Deng J,et al.Time series analysis of influenza incidence in Chinese provinces from 2004 to 2011.Medicine,2016,95(26):e3929.

[3]Li XX,Wang LX,Zhang H,et al.Seasonal variations in notification of active tuberculosis cases in China,2005-2012.Plos One,2013,8(7):e68102.

[4]陈正利,陈伟,许汴利.应用ARIMA模型对河南省1991-2011年乙型肝炎发病趋势分析.中国卫生统计,2013,30(3):401-402.

[5]朱玉.单纯ARIMA模型和ARIMA-GRNN组合模型在猩红热月发病率中的预测效果比较.合肥:安徽医科大学,2011.

[6]朱奕奕,冯玮,赵琦,等.ARIMA乘积季节模型在上海市甲肝发病预测中的应用.复旦学报(医学版),2012,39(5):460-464.

[7]时照华.探索ARIMA模型在呼吸道传染病疫情预测中的应用.合肥:安徽医科大学,2013.

[8]董晶.长沙市手足口病疫情分布特征及预测模型的建立与评估.长沙:中南大学,2014.

[9]陈伟,陈正利,李少芳,等.ARIMA模型在河南省梅毒月发病率预测中的应用.中国卫生统计,2013,30(4):604-606.

[10]薛允莲,张晋昕,刘贵浩,等.医院住院人数序列的春节效应调整.中国卫生统计,2010,27(5):473-476.

[11]王玖,韩春蕾,栾奕昭.组合预测在医院门诊量预测中的应用.中国卫生统计,2012,29(6):881-883+886.

[12]郭志武,蒲继红,滕国召.基于ARIMA模型的春节因素调整方法研究.中国卫生统计,2009,26(6):573-576+579.