SKAT与惩罚回归模型两阶段策略在基因组关联研究中的应用*
2017-07-18广东药科大学公共卫生学院流行病与卫生统计学系510310
广东药科大学公共卫生学院流行病与卫生统计学系(510310)
张俊国 林志丰 刘 丽 李丽霞 杨 翌 郜艳晖△
SKAT与惩罚回归模型两阶段策略在基因组关联研究中的应用*
广东药科大学公共卫生学院流行病与卫生统计学系(510310)
张俊国 林志丰 刘 丽 李丽霞 杨 翌 郜艳晖△
目的 本研究提出两阶段分析策略,将SKAT与惩罚回归模型联合应用,为遗传关联研究提供方法学选择的依据和指导。方法 本研究使用遗传分析工作组18的数据,分别采用SKAT,LASSO,EN,cMCP,Gel以及两阶段统计分析策略(SKAT+EN,SKAT+LASSO,EN+SKAT,LASSO+SKAT)进行关联性分析。结果 在基因水平,SKAT法的平均灵敏度与约登指数最高。除SKAT法外,其余统计策略的关联基因选出率均与对结局方差解释的比例和基因中包含SNPs的数目存在关联。在SNPs水平,EN法与EN+SKAT的灵敏度与约登指数最高。不同的统计策略均能把对结局效应贡献最大的真关联基因MAP4与SNPs筛选出来。结论 SKAT和EN联合分析策略能够在数百万SNPs中筛选主要的疾病关联基因与SNPs,并在基因水平上统计推断,有着较高灵敏度,同时还能控制严重的假阳性错误,为遗传关联研究提供了一种较为高效的统计分析策略。
SKAT 惩罚回归模型 基因组关联研究
在基因组关联研究中,单位点关联性检验受限于严苛的多重校正显著性水平,其效能极低[1]。基于个体间遗传相似性的方差分量检验SKAT(sequence kernel association test)将多个SNPs(single nucleotide polymorphisms)聚集成组,不仅增加效能,还可处理位点间连锁不平衡及位点效应方向不同等问题[2]。但SKAT只在组水平上进行推断,无法得到单个位点的效应,限制了后续功能学研究的线索。由于基因组关联数据呈现高维、噪音大、连锁不平衡等特征[3],在传统最小二乘与似然估计基础上引入惩罚函数是解决此类问题的有效工具,自1996年Tibshirani提出LASSO(least absolute shrinkage and selection operator)后,惩罚回归模型广受关注,基于惩罚思想发展了许多统计学方法[4],如LASSO和岭回归结合的EN(elastic net)[5],与LASSO都可在大幅降维的同时估计单个变异的效应。考虑到位点间的相互作用和增加效能,也可同时在组水平和位点水平上惩罚,如cMCP(composite minimax concave penalty)[6]和GEL(group exponential lasso)[7]等,但各类方法应用效果仍有待于进一步研究。
本研究基于同时在组水平和位点水平上推断的思路,尝试将SKAT与LASSO和EN联合,应用两阶段策略进行关联性分析,并与单水平及成组惩罚模型(cMCP和GEL)进行比较以评价各类方法的性能,为遗传关联研究方法学选择提供依据和指导。
统计方法原理
假设有n个观测,第i个研究对象的P个SNPs基因型数据表示为xi=(xi1,xi2,…,xiP)T,i=1,2,…,n;其中xip=0,1,2(p=1,2,…,P)分别对应主要等位基因的纯合子、杂合子以及最小等位基因的纯合子,根据生物学先验,将待分析的P个SNPs分成J组(如以基因为组单位),Qj为第j组中的SNPs个数(q=1,2,…,Qj);进一步假设xip已被中心化。每个研究对象有K个人口学、环境或其他混杂因素,用Zi=(zi1,zi2,…ziK)T来表示。第i个研究对象的表型状态为yi∈R。
1.SKAT
SKAT以SNPs集(如基因、通路或ROI)为分析单位,在线性混合效应模型的框架下,通过核函数(kernel function)量化个体间的遗传相似性,并基于得分函数(score function)进行方差成份检验[8],当表型性状为连续型变量时,模型为
yi=β0+β1zi1+…+βKziK+h(xi1,xi2,…xiQj)+εi
(1)
式(1)中β0是截距项,β1,…,βK表示环境或人口学特征等协变量的回归系数,εi为随机误差,服从N(0,σ2)。核函数h(·)综合了集合中所有SNPs的遗传信息,选择不同形式的核函数可拟合集合内SNPs与表型的线性或非线性关联[9-10]。
2.LASSO和EN

(2)
式(2)中λ≥0,为惩罚参数,用于控制压缩程度。
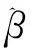
(3)
可看出,式(3)中当α=1时为L2惩罚,即岭估计,当α=0时为L1惩罚,则为LASSO;实际应用中一般α取0.5。λ为调整参数,意义同式(2)[11]。研究显示EN比LASSO可得到更加稳定、精准的预测,适用于基因微阵列等高维且存在共线性的小样本[12]。
3.cMCP和GEL
类似SKAT集合SNPs的思想,有学者提出运用惩罚模型分析SNPs效应时也应考虑组(SNPs集)的选择,即不仅选择重要的成组,同时选择组内重要的变量[13]。Breheny等在2009年提出分层惩罚的结构[6]:
(4)
式(4)中fλ,b与fλ,a分别代表组水平与SNPs水平的惩罚函数。
cMCP在两水平均使用MCP惩罚函数进行筛选,具有无偏性、稀疏性和连续性等性质,其惩罚函数和导函数分别定义为[6,14]:
(5)
式(5)中λ是决定惩罚大小的正则化参数,a是影响惩罚函数应用范围的调节参数,如式(4)中组内和组外调节参数分别为a和b;当结局变量和协变量标准化时,推荐使用a=3[6]。式(4)中的b是组外惩罚的调节参数,为了使组水平的惩罚达到自身的最大值,可设为Qjγa/2。
在分层惩罚结构的基础上,Breheny进一步尝试非凸的指数惩罚函数[7],即:
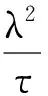
(6)
将式(6)运用于分层惩罚的结构,如式(4)中称为group exponential lasso。可证明当τ趋于0时,式(6)退化为L1惩罚。模拟研究显示,当组外使用指数惩罚函数(经验值τ=1/3),组内使用L1惩罚时(称GEL),该法运用变量的分组信息,同时在组水平和变量水平进行选择,其估计准确性优于成组LASSO和cMCP[7]。
上述惩罚回归模型的拟合均使用坐标下降法(coordinate descent)[15]或由其改进的局部近似坐标下降法(locally approximated coordinate descent)[6]。调整参数的确定则通过K折交叉验证、广义交叉验证、无偏估计的风险分析以及BIC准则等[16]。所有方法均可在R3.2.2软件实现,分别调用软件包SKAT(SKAT)glmnet(LASSO和EN),grpreg(cMCP和GEL)。
模拟实例分析
1.数据来源
本研究数据源于遗传分析工作组18(genetic analysis workshop 18,GAW18)[17],是一个国际上公开的用于研究稀有变异关联方法的模拟数据平台。本文选择性别、年龄和血压均无缺失的849个存在亲缘关系的个体作为研究对象,将3个时间点的舒张压(DBP)均值作为结局变量,选取对DBP方差解释比例最大(7.79%)的3号染色体中SNPs作为自变量。先通过UCSC基因浏览器(http://hgdownload.soe.ucsc.edu/goldenPath/hg19/database/refGene.txt.gz/)对3号染色体的全部SNPs(共1215399个)进行基因标记,基因的范围为最小的转录起始位点到最大的转录结束位点之间;再删除基因间与存在缺失的SNPs后,最终共标记1141个基因的532092个SNPs,其中MAF低于1%的稀有变异占51%。纳入分析的532,092个SNPs中与DBP存在真关联的基因(SNPs)有35(119)个,真关联位点解释DBP的方差比例为7.27%。其中,对DBP效应最大的基因为MAP4,解释的方差比例为6.48%。
2.评价方法及策略
GAW18提供了200个和遗传变异有关联的模拟表型数据集,考虑到计算负担,本研究分析其中50个。对每个数据集,分别采用SKAT,LASSO,EN,cMCP,GEL以及两阶段联合分析策略(SKAT+EN,SKAT+LASSO,EN+SKAT,LASSO+SKAT)进行关联性分析,其中联合策略如SKAT+EN表示先用SKAT筛选,将结果阳性的基因(SNPs)再纳入EN进行分析。由于SKAT只在基因水平上评价,故本研究中SKAT分析时选入的基因及其SNPs均视为阳性。LASSO和EN只在SNPs水平上评价,则模型中系数不为0的SNPs及所属基因均视为阳性。
为评价各统计方法识别真关联基因(SNPs)以及剔除非关联基因的能力;本研究在基因水平和SNPs水平上分别计算50个数据集中各方法的平均灵敏度(%)、特异度(%)和约登指数(%)。其中灵敏度定义为:各方法筛选出的真关联基因(SNP)的数目除以基因组中实际关联基因(SNP)的总数;特异度定义为:各方法剔除的非关联基因(SNP)的数目除以基因组中实际非关联基因(SNP)的总数;约登指数定义为灵敏度+特异度-1。进一步采用Spearman相关系数(rs)评价各方法选入的基因中基因解释DBP方差的比例、基因内包含的真关联SNPs数目与基因选入率(50次运算中某基因选入的比例)的关系。其中SKAT法、cMCP和GEL均以基因作为组水平。因为Bonferroni校正过于苛刻,故SKAT法采用FDR法进行多重校正。惩罚回归中调整参数确定均采用10折交叉验证。所有统计分析中均忽略有亲缘关系个体间的家庭相关。
结 果
GEL在50个数据集中模型均无法收敛,SKAT法只在基因水平上评价,因此后续在基因水平上评价8种方法,在SNPs水平上评价7种方法。
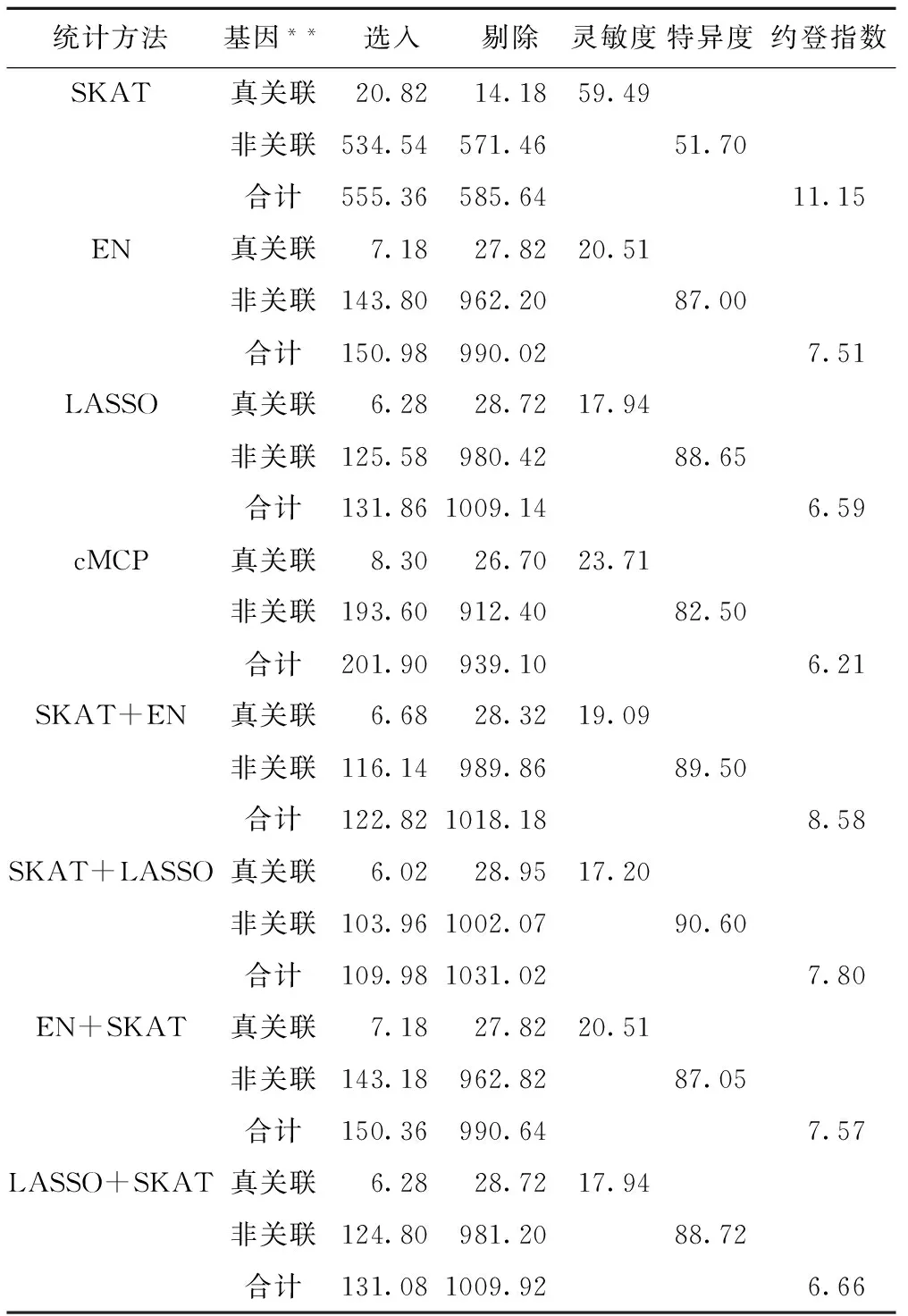
表1 在基因水平上各类方法的平均灵敏度(%)、特异度(%)和约登指数(%)*
*50个模拟数据集分析结果;**真关联和非关联基因数分别为35和1106个。
各方法在基因水平的评价结果见表1。可以看到,SKAT法的平均灵敏度最高,为59.49%;SKAT+LASSO的特异度值最高,为90.60%。SKAT法的平均约登指数最高,为11.15%,其次是SKAT+EN,为8.58%。
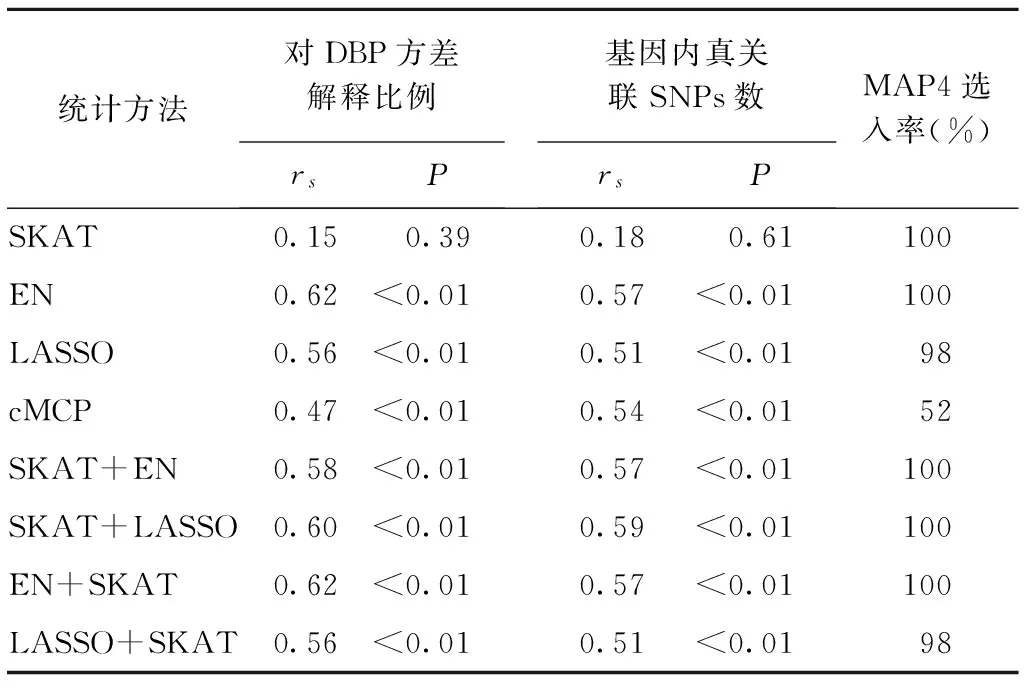
表2 在基因水平上各方法基因选入率与基因效应的关系
如表2所示,除SKAT法外,其余方法基因选入率均与基因效应有关,基因解释DBP方差比例越大、基因内真关联SNPs数越多,则越容易被选入。对DBP效应最大的基因MAP4,除cMCP外,其他方法在50次模拟中选入率均较高(98%~100%)。

表3 在SNPs水平上各类方法的平均灵敏度(%)、特异度(%)和约登指数(%)*
*:50个模拟数据集分析结果;**:真关联和非关联SNPs数分别为119和531971个。
各方法在SNPs水平的评价结果见表3。可知各法灵敏度都较低,特异度均较高。相较之下,EN法与EN+SKAT的平均灵敏度最高。在特异度指标上,LASSO与其两阶段的分析策略最高。约登指数最高的为EN+SKAT与EN。
讨 论
在全基因组关联研究中,从浩瀚如烟的遗传变异中筛选与疾病存在关联的少数病因变异对统计方法提出巨大的挑战。SKAT与惩罚回归模型是近年来热门的遗传统计方法;SKAT理论上有吸引力且计算快捷,在基因水平上灵敏度高,可筛选更多的真关联基因。惩罚回归模型具有良好的预测精度与稳定性,能够在数十万SNPs中大幅度压缩,挑选出与疾病关联性最强的基因与SNPs;但与以往研究[18]一致,单独使用惩罚回归模型仍会产生大量的假阳性,需要在独立人群中进一步验证。本研究将两法结合,结果表明,可将更多真关联基因(SNPs)纳入后续分析(SKAT+LASSO、SKAT+EN)或对结果做进一步筛选(LASSO+SKAT、EN+SKAT)。在基因水平上,SKAT的性能最高,其余方法中两阶段策略的性能略优于单一策略。在SNPs水平上,EN法与EN+SKAT的性能略高于其它策略。
尽管两水平惩罚模型理论合理,但本研究显示在基因组关联研究中,cMCP的性能指标均低于其余统计分析策略,并未表现出优势。该法在SNPs水平上的性能与LASSO相差无几,对变量系数的两次压缩并不能很大程度上减少方差,反而引入不必要的偏差,损失了更多的真关联SNPs[7]。此外,GEL法在本研究所有数据中模型均无法收敛,当变量数远远大于观测数的时候,该法可能无法在较低的β值上实现模型拟合,此时模型无法识别或接近于奇异,系数的路径也不存在。
本研究还显示除SKAT外,各方法中关联基因的选入率均与基因效应有关。MAP4作为效应最大的基因,内含最多的真关联SNPs;除cMCP法外,MAP4在50次试验里几乎均能被选出,系数值前列的SNPs亦是如此。此结果与以往运用GAW18数据评价遗传统计方法的研究结果基本一致[19]。
限于GAW18中非独立个体样本量过低,本文选用了有亲缘关系的研究对象,进一步研究中可在模型中纳入随机效应或采用边际模型以解释家庭成员表型相关。此外,从进化角度而言,稀有变异比常见变异更可能具有较强的生物学功能及遗传效应。如定义稀有变异的阈值并施加一定权重,可能会提高统计分析的效能。
[1]Gang P,Li L,Hoicheong S,et al.Gene and pathway-based second-wave analysis of genome-wide association studies.European Journal of Human Genetics Ejhg,2010,18(1):111-117.
[2]Wu M,Lee S,Cai T,et al.Rare-variant association testing for sequencing data with the sequence kernel association test.American Journal of Human Genetics,2011,89(1):82-93.
[3]张秀秀,王慧,田双双,等.高维数据回归分析中基于LASSO的自变量选择.中国卫生统计,2013,30(6):922-926.
[4]Tibshirani R.Regression Shrinkage and Selection via the Lasso.Journal of the Royal Statistical Society,1996,58(1):267-288.
[5]Zou H,Hastie T.Regularization and variable selection via the elastic net.Journal of the Royal Statistical Society,2005,67(2):301-320.
[6]Breheny P,Huang J.Penalized methods for bi-level variable selection.Statistics & Its Interface,2009,2(3):369-380.
[7]Breheny P.The group exponential lasso for bi-level variable selection.Biometrics,2015,71(3):731-740.
[8]曾平,赵杨,陈峰.新一代测序数据的罕见遗传变异关联性统计方法.中国卫生统计,2015,32(6):1091-1096.
[9]Brown MP,Grundy WN,Lin D,et al.Knowledge-based analysis of microarray gene expression data by using support vector machines.Proceedings of the National Academy of Sciences.2000,97(1):262-267.
[10]Liu D,Ghosh D,Lin X.Estimation and testing for the effect of a genetic pathway on a disease outcome using logistic kernel machine regression via logistic mixed models.Bmc Bioinformatics.2008,9(14):292.
[11]张俊国,刘丽,李丽霞,等.惩罚广义线性模型在遗传关联研究中的应用及R软件实现.中国卫生统计,2016,33(4):582-586.
[12]Hesterberg T,Choi NH,Meier L,et al.Least angle and1 penalized regression:A review.Statistics Surveys.2008,2.
[13]Huang J,Ma S,Xie H,et al.A group bridge approach for variable selection.Biometrika,2009,96(2):339-355.
[14]Zhang CH.Nearly unbiased variable selection under minimax concave penalty.Annals of Statistics,2010,38(2):894-942.
[15]Friedman J,Hastie T,Tibshirani R.Regularization paths for generalized linear models via coordinate descent.Journal of Statistical Software,2009,33(1):1-22.
[16]Fu WJ.Nonlinear GCV and quasi-GCV for shrinkage models.Journal of Statistical Planning & Inference,2005,131(2):333-347.
[17]Laura A,Dyer TD,Peralta JM,et al.Data for Genetic Analysis Workshop 18:human whole genome sequence,blood pressure,and simulated phenotypes in extended pedigrees.Bmc Proceedings,2014,8(1):1-9.
[18]勾建伟.惩罚回归方法的研究及其在后全基因关联研究中的应用.南京医科大学,2014.
[19]Cordell HJ.Summary of Results and Discussions From the Gene-Based Tests Group at Genetic Analysis Workshop 18.Genetic Epidemiology,2014,38 Suppl 1(S1):S44-S48.
(责任编辑:郭海强)
Two-steps Strategies Jointing SKAT with Penalized Regression and their Application in Genome-wide Association Study
Zhang Junguo,Lin Zhifeng,Liu Li,et al
(DepartmentofEpidemiologyandBiostatistics,SchoolofPublicHealth,GuangdongPharmaceuticalUniversity(510310),Guangzhou)
Objective This study proposes two-stage analysis strategy to combine the advantages of two types of methods in order to provide a method guidance for the genetic association study.Methods SKAT,LASSO,EN and two-stage strategies(SKAT+EN,SKAT+LASSO,EN+SKAT,LASSO+SKAT)as well as bi-level variable selection models(cMCP,Gel)are used in the data of the genetic analysis workshop 18 to compare their application performance.Results At the gene level show that the method of SKAT has the highest average sensitivity and average Youden index.The rate of gene of these statistical methods except the method of SKAT are associated with the number of SNPs within the gene and the proportion of explained variance of DBP.The result at the SNP level indicate that the method of EN has highest sensitivity.The highest Youden index is counted by EN+SKAT method and the second is EN method.The gene of MAP4 and SNPs that is the largest contribution to DBP all selected by the various statistical analysis.Conclusion The combination of the methods of EN and SKAT could screen few number variants that associate with phenotypes in big data.This methods not only has high sensitivity but also has restraint false positives,it could provide some clues for the future studies of genetic mechanisms.
SKAT;Penalized regression;Genome-wide association study
国家自然科学基金(81302493);广东省科技厅社会发展基金(2014A020212307);广东省自然科学基金(2016A030313809)
△通信作者:郜艳晖,E-mail:gao_yanhui@163.com。
