基于波束空间的多重信号分类算法
2017-07-18聂益芳重庆工商大学
聂益芳 重庆工商大学
基于波束空间的多重信号分类算法
聂益芳 重庆工商大学
针对在实际应用环境中偏差和扰动不可避免的情况,提出了基于波束空间的多重信号分类算法。通过引入波束空间预处理技术来对误差进行校正,经过理论和仿真分析验证,基于波束空间MUSIC的算法估计方差比经典MUSIC算法大,但是它的信噪比门限明显降低且计算量更小。
谱估计 波束空间 多重信号分类 误差
空间谱估计的目标空间由信号源的参数和复杂的空间环境参数构成,谱估计是用某种特定的方法从目标空间中得出与信号源相关的某些想要知道的参数或者属性。观察空间,物理上是按一定方式排列的阵元,实际应用中通过阵元来接收目标空间的信号源。传统的空间谱估计算法,已经不能再进行有效的测向,出现了计算量小而且便于实现的空间平滑技术,但空间平滑技术是以有效阵元数为代价,对阵列孔径会产生一定的影响,而且它的算法性能在低信噪比的情况下很差。
1 理论模型
基于波束空间的多重信号分类空间谱估计方法(B-MUSIC),先将物理空间的阵元合成为一个或者几个波束,然后再利用合成后的波束数据进行空间谱估计。其原理图如图1。
假设在窄带远场条件下, M元均匀线阵的阵元间距d为半波长,且阵列的导向矢量为




图1 基于波束空间的DOA估计原理

2 性能理论分析
波束形成矩阵的取值不同时对阵列的影响不同,接下来从克拉美—罗界和波束增益两个方面来对波束空间MUSIC算法的性能进行讨论。
2.1 波束增益
波束增益的表达式定义为


结合上述对误差的理论分析,下面通过仿真来验证基于波束空间的多重信号分类算法性能。
3.1 波束增益和方位角之间的关系
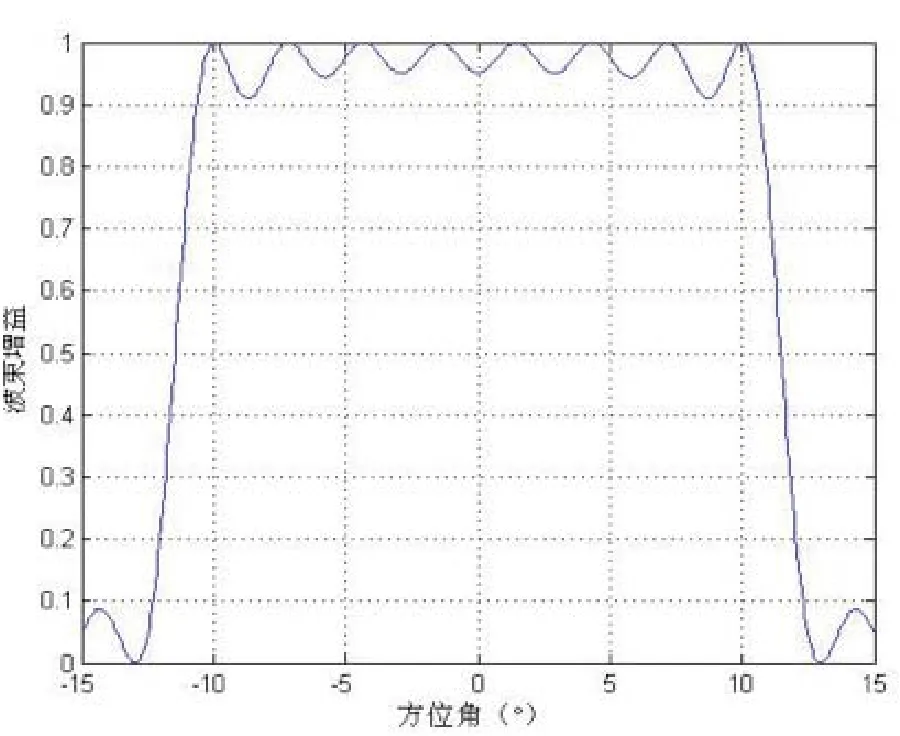
图2 方位角对波束增益的影响
由图2可知当方位角为-10°≤θ≤10°时,虽然波束增益的值一直起伏,始终等于1或者小于且接近于1,满足增益的条件。
3.2 B-MUSIC算法和经典MUSIC算法克拉美—罗限比较
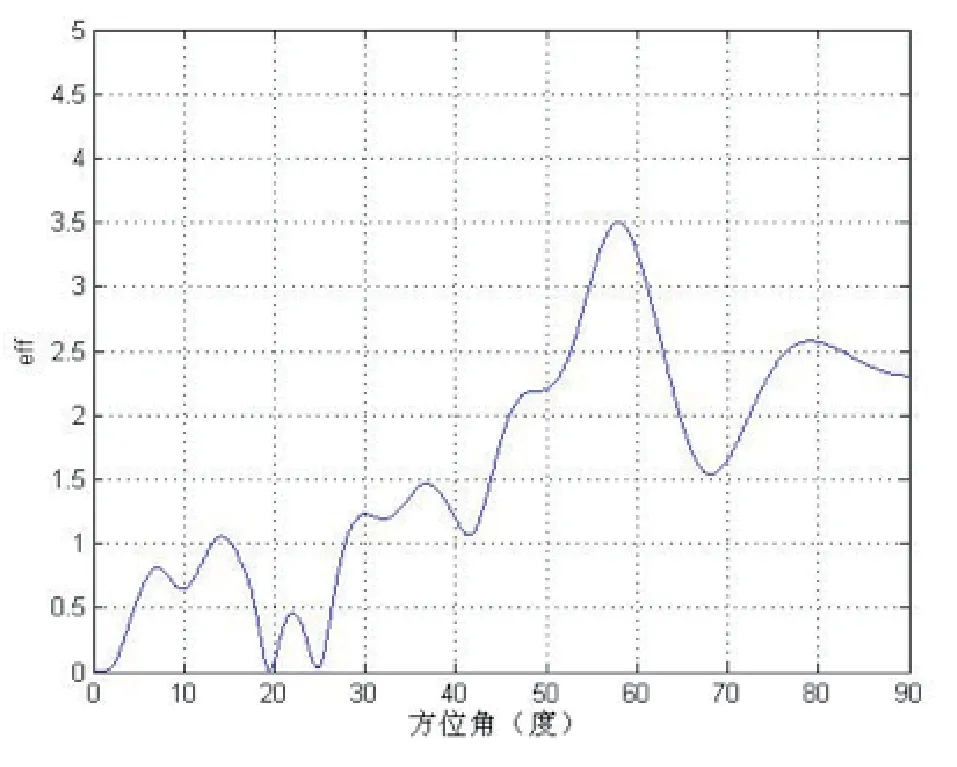
图3 B-MUSIC和经典MUSIC算法性能比较
由图3可知,MUSIC算法的均方误差一般情况下都比B-MUSIC算法的小。因为两个窄带远场信号不相关,又B-MUSIC算法和MUSIC算法在相关系数为0的时候最接近CRB罗界,证明见文献[1]。
4 结束语
存在阵列误差下MUSIC算法的性能严重下降,基于波束空间的空间谱估计方法,先将物理空间的阵元进行合成为一个或者几个波束,然后再利用合成以后的波束数据进行空间谱估计。该算法主要优点是系统复杂度更低。当波束数和阵元数目相等的时候,使用波束预处理技术的算法一般的MUSIC算法的性能相同。
[1]王永良,陈辉,彭应宁,万群.空间谱估计理论与算法[M],北京:清华大学出版社,2004
[2]Weiss A J,Friedlander B.Effects of modeling errors on the resolution threshold of the MUSIC algorithm.IEEE Trans.on SP,1994,42(6):1519-1526
