基于有限元的天平校准系统基座结构优化设计

赵永丰+王均涛

摘要： 在Solidworks环境下建立三维模型，运用有限元软件对基座结构进行动、静态性能分析，得到初始模型的性能参数.以最小质量为目标函数，以刚度、应力和频率为约束条件，建立数学模型.提出一种基于渐进结构优化法的拓扑优化方法，引入过滤函数来解决拓扑优化过程中容易出现的数值不稳定、数值分布呈棋盘模式的现象，保证计算结果的准确性.对拓扑优化后的模型重新分析计算后发现，其性能依然优异，基频提升26.7%，质量减少5.8%.

关键词： 基座； 静力分析； 模态分析； 拓扑优化； 渐进结构优化

中图分类号： TH 715文献标志码： A

Optimization Design of Pedestal Structure of Balance

Calibration System Based on Finite Element Method

ZHAO Yongfeng1，WANG Juntao2

（1.School of Mechanical Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China；

2.Shanghai Machine Tool Works Ltd.， Shanghai 200093， China）

Abstract： The threedimensional model is established in Solidworks，and the static and dynamic performance of the pedestal structure is analyzed by finite element software，which can help to get the performance parameters of the initial model.Based on the minimummass as the objective function，the mathematical model for topology optimization is established with the stiffness，stress and frequency as the constraint condition.For ensuring the accuracy of the calculation results，a method based on evolution structure optimization for topology optimization is presented and a filtering function is introduced in order to solve the numerical instability and checkerboard phenomenon in the topology optimization process.After analyzing the calculation of the topological optimized model，the structure performance is still excellent.As a result，the fundamental frequency increased by 27.6%，and the mass reduced by 5.8%.

Keywords： pedestal； static analysis； modal analysis； topology optimization； evolution structure optimization

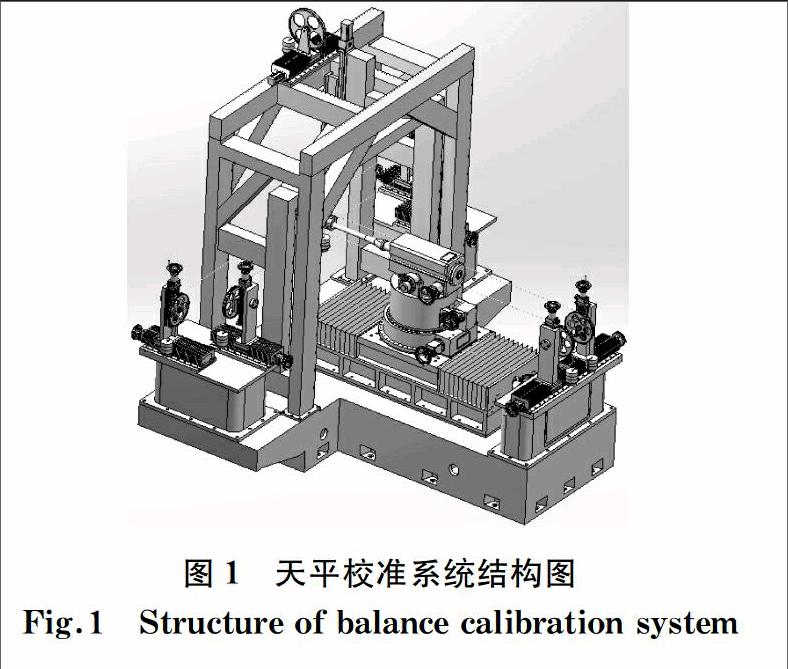
风洞天平校准系统是目前世界各国在各类型气动力测量试验中广泛采用的测量装置，其性能指标直接影响天平校准系统的试验测量数据精度.风洞天平校准装置主要由龙门架、基座和四自由度机械台体组成，其系统结构如图1所示.基座支撑龙门架、加载机构和四自由度机械台等部件，在整个系统中占总质量的44.6%.因此，在保证刚度和强度的情况下，合理设计基座结构，进行拓扑优化，以使基座质量减小，同时降低工艺难度与生产成本，获得良好的经济效益.基座内部的筋板结构和布局在很大程度上決定了基座的动、静态性能[1]，而基座静态特性与动态特性又影响着天平校准系统的测量性能与精度稳定性.低阶模态特性基本决定了产品的动态性能，因此，在基座结构优化过程中也要考虑频率方面的约束[2].对天平校准系统的基座进行静力分析与模态分析，利用渐进结构优化法，以最小质量为目标函数，以刚度、应力和频率为约束条件，引入过滤函数来解决拓扑优化过程中容易出现的数值不稳定现象.最后对基座进行拓扑分析，从满足约束的结构中删除多余的材料，以此来获得最小的基座质量.

1.1模型建立

基座由灰铸铁铸造而成，结构复杂多变，主要由厚度不一、形状各异的筋板，以及铸造岀砂孔构成，根据实际使用情况需要，整体结构形状设计为T型.Solidworks环境下建立的三维模型是有限元分析和结构优化的前提和基础.为了便于有限元分析计算，必须对三维模型进行结构简化，省去倒角、圆角、螺纹孔等细微特征.简化后的模型及有限元模型如图2、图3所示.基座长3 100 mm，两翼宽2 990 mm，中间宽1 260 mm，高520 mm，设定中间筋板厚度25 mm，两翼筋板厚度20 mm，壁厚25 mm.

1.2静力分析

静力分析用于计算在固定不变的载荷作用下结构的效应，它不考虑惯性和阻尼的影响，如结构随时间变化的载荷的情况.其静力学方程为：

[K]{u}={F}（1）

式中：[K]为刚度矩阵；{u}为各节点位移；{F}为静力载荷.

在静态工作环境下，基座主要受到3个相同的侧力加载机构的重力，其值均为9 000 N，四自由度机械台重力约为30 000 N，龙门架及其上的测量架与升力加载机构的重力约为20 000 N.在ANSYS软件中设置材料、划分网格、施加约束和作用力，得到变形与应力分布图，如图4、图5所示.

由图4可知，最大变形为0.015 mm，最大应力为1.47 MPa.最大变形发生于基座两翼部分，此处正是侧力加载机构所处的位置，而这个系统最关键的部分就是此处的侧力加载机构，其精度直接影响测量的准确度.应力范围为0.16～1.47 MPa，远远小于铸铁的极限强度，基座可以进一步减轻质量.

1.3模态分析

模态是结构的一种固有振动特性，是一种研究结构动力特性的方法.每个结构都具有各自的模态参数，而模态参数的识别大致分为两种方法：一是通过计算机的有限元软件进行计算获得；另一种是模态试验的方法，通过试验设备采集到输出信号，经过参数识别从而获得模态参数.本文采用有限元软件进行计算获取模态参数.

自由度的振动系统可表示为[3]：

[M]{x··}+[ξ]{x·}+[K]{x}={f}（2）

式中：[M]，[K]分别为质量和刚度矩阵；{f}为外激励矩阵；{x··}、{x}分别为物理坐标下的位移和加速度矩阵.

当{f}=0时，阻尼ξ=0，式（2）为自由振动方程，其特征方程为：

[K]-ω2[M]=0（3）

解方程式（3）得ω的m个互异正根ω0i（i=1，2，…，m），并按升序排序，0<ω01<ω02<…<ω0m，第i阶固有圆频率

ω0i=kimi或固有频率f0i=12πkimi（4）

各阶固有频率f0i均与kimi成正比，f0i越大，说明单位质量的刚度越高，可作为结构动态设计的一个优化约束条件.在进行动态结构优化时，尽量提高各阶固有频率，避免固有频率与外界激励频率一致引起共振.利用ANSYS软件对基座进行模态分析，分析时采用静力分析模型，对基座底面进行固定约束，不施加任何载荷，由于低阶模态对振动系统影响较大，求得基座的前四阶频率，如表1所示.各阶振型如图5所示.

通过对基座进行自由模态分析，得到了基座的固有频率和固有振型，真实地反映出基座的动态特性.表1和图6表明基座具有良好的振动性能，同时也为后续基座结构优化分析设计做了准备.

2基座的拓扑优化

静力学方面的拓扑优化问题一般可以按两种方式建立优化模型：一是在体积或质量约束下求最小柔度，即最大刚度；二是在刚度（或其他条件）约束下求最小体积或质量[4].本文是在频率、刚度及应力约束下采用渐进结构优化法（evolutionary structural optimization，简称ESO法[5-6]）求解最轻的质量.

所谓ESO法就是预先选取结构设计域和初始域，给定结构所需满足的目标函数和约束条件的贡献度.根据其贡献度大小删除无效的材料，循环该过程，达到终止条件，最终得到最佳拓扑结构.在优化迭代过程中，采用固定的有限元网格，对存在的材料单元，其材料数编号为非零的数，而对不存在的材料单元，其材料数编号为零，通过这种零和非零模式实现结构拓扑优化.该方法具有良好的通用性，能够采用已有的有限元分析软件，通过迭代，在计算机上实现.

2.1静力优化准则

2.1.1应力准则

在某一结构中，如果某一部分的材料没有得到充分的利用，应将其删除或改进，如此反复进行，直至得到最优应力分布[7].基于此原理，通过对基座进行应力分析，确定单元的Von Mises应力σvme与整个结构的最大Von Mises应力σvmmax，然后删除不满足条件的单元，减小基座质量.对于各项同性的材料，其Von Mises应力定义为：

σvm=σ2x+σ2y-σxσy+3τ2xy（5）

式中：σx和σy分别为x和y方向的正应力；τxy为剪应力.

将单元的Von Mises应力σvme与整个结构的最大Von Mises应力σvmmax进行比较，便可确定每个单元的应力水平.在每一次有限元分析后，从模型中删除满足下列条件的所有单元：

σvmeσvmmax

式中，RRi为当前的拒绝率.

采用相同的拒绝率，反复迭代有限元分析和单元删除循环，直至达到稳态，然后引进一个进化率ER，并附加到拒绝率中，即：

RRi+1=RRi+ER， i=0，1，2，…（7）

用这个增加的拒绝率再一次进行有限元分析和单元删除，直至达到一个新的稳态.

2.1.2刚度准则

对基座而言，在改变其结构时，必须保证其刚度，但是部分材料的刚度不会对结构整体产生很大的影响，因此类比于应力准则将没有得到充分利用的材料删除，以此减小基座的质量.根据式（1），结构的平均柔顺度，即刚度的对立量：

C=12[F]T[K]-1[F]（8）

在载荷向量不变的情况下，整体刚度的最大化也就是结构柔顺度的最小化.从结构中删除第i号单元时，式（1）就变为：

（[K]-[Ki1]）·（[u]+Δ[u]）=[F]（9）

式中：[Ki1]為对第i号单元扩维了的刚度矩阵；Δ[u]为位移向量的变化.

用式（1）减去式（9），并忽略式（9）中的高阶量，得到位移的变化量：

Δ[u]=[K]-1[Ki1][u]（10）

将式（10）带入式（8）得：

ΔC=12[F]TΔ[u]=12[F]T[K]-1[Ki1][u]=

12[u]T[Ki1][u]=12[ui]T[Ki][ui]（11）

式中：[Ki]为第i号单元的刚度；[ui]为第i号单元的位移向量.

由此得到第i号单元的灵敏度：

αi=[ui]T[Ki][ui]（12）

式中：αi表示删除第i号单元时的结构柔顺度的变化情况.

优化目标就是寻找刚度约束的最轻结构，给出如下的约束：

C≤C*（13）

式中：C*为C的上限.

为了达到优化结果，在优化过程中删除αi值最小的单元，以使得C的增加量最小.

2.2建立数学模型

根据上述分析，基座具有良好的动态性能，其一阶频率远高于基座上电机的频率（25 Hz），因此限定某一固定频率，以频率、刚度、应力作为约束，最小质量作为目标函数建立如下数学模型：

findMinM

s.t.f=fd

C≤C*

σvmeσvmmax≤1%（14）

式中：M为基座的质量；fd为基座的某一固有频率.

在优化拓扑过程中容易出现数值计算不稳定的情况，产生类似棋盘格的模式.可以通过引入过滤函数[8-11]来抑制棋盘格，对单元的灵敏度进行松弛调整，避免相邻单元灵敏度相差悬殊.将编号为1到j-1的单元灵敏度通过权系数μij加到第j个单元上，即：

u′j=∑i

定义加权系数：

μij=d（i，j）∑Nj=1d（i，j）

定义单元灵敏度：

u′i=∑ji=1d（i，j）ui∑ji=1d（i，j）（15）

式中：d（i，j）=R-D（Ni-Nj）；D（Ni-Nj）为单元i到单元j的距离；R为过滤半径，其值为2倍的网格单元边长.

2.3优化结果分析

依据上述数学模型，设定基座质量下降20%，对基座进行拓扑优化，优化后的拓扑图如图7所示.图7中深黑色材料部分表示应该切除，但是出于实际制造、加工和使用等方面考虑，不是所有的部分都应该完全切除，也可以采取减小厚度的办法，降低基座的质量.另外，图7中认为要保留的部分，出于实际考虑有些部分也应该删除.例如，在铸造时，需要设置铸造出砂孔，就应在内部筋板上合理布置一些岀砂孔，优化后的基座结构如图8所示.

对优化后的基座结构进行有限元分析，优化前后性能参数如表2所示.基座最大应力由原来的1.47 MPa变为2.16 MPa，但仍满足强度要求，最大变形基本无变化，说明整体刚性良好，基频增加了47.8 Hz，质量由原来的5 970 kg减小到5 620 kg，减小了5.8%.

3结论

在正确建立模型结构的基础上，对模型做了静力、模态分析，得到了初始模型的静、动态性能参数，分析了各参数对基座性能的影响.运用ESO法对基座进行拓扑优化，减小了基座质量，且整体刚性良好，基频得到了提升，达到了预期的目标.

參考文献：

[1]陈叶林，丁晓红，郭春星，等.机床床身结构优化设计方法[J].机械设计，2010，27（8）：65-68.

[2]倪晓宇，易红，汤文成，等.机床床身结构的有限元分析与优化[J].制造技术与机床，2005（2）：47-50.

[3]张学玲，徐燕申，钟伟泓.基于有限元分析的数控机床床身结构动态优化设计方法研究[J].机械强度，2005，27（3）：353-357.

[4]焦洪宇，周奇才，李文军，等.基于变密度法的周期性拓扑优化[J].机械工程学报，2013，49（13）：132-138.

[5]林丹益，李芳.基于ANSYS的结构拓扑优化[J].机电工程，2012，29（8）：898-901.

[6]荣见华，葛森，邓果，等.基于位移和应力灵敏度的结构拓扑优化设计[J].力学学报，2009，41（4）：518-529.

[7]荣见华.渐进结构优化方法及其应用研究[D].长沙：国防科学技术大学，2006.

[8]HUANG X D，XIE Y M.Optimal design of periodic structures using evolutionary topology optimization[J].Structural and Multidisciplinary Optimization，2008，36（6）：597-606.

[9]叶红玲，沈静娴，隋允康.过滤函数对应力约束连续体结构拓扑优化的影响分析[J].北京工业大学学报，2013，39（3）：321-330.

[10]叶红玲，李耀明，张颜明，等.基于对数型Heaviside近似函数作为过滤函数的动力响应结构拓扑优化ICM方法[J].工程力学，2014，31（6）：13-20.

[11]尚珍，隋允康.结构拓扑优化中不同过滤函数间关系的探讨[J].力学与实践，2011，33（2）：52-57.有色金属材料与工程第38卷第3期NONFERROUS METAL MATERIALS AND ENGINEERINGVol.38No.32017

文章编号：2096-2983（2017）03-0172-05DOI：10.13258/j.cnki.nmme.2017.03.009