最短路径算法的图示解析

王秋荟+陈继斌

摘要：随着科学技术的发展，最短路问题在生活中应用得越来越广泛，所以研究最短路径问题有非常的重要意义。通过对Dijkstra、Floyd两种最短路算法进行图示解析，能让我们更好地理解算法思想以及求最短路径的过程，进而将其应用在实际工程的优化设计中。

关键词：最短路径；Di]kstra算法；Flovd算法

中图分类号：TP301 文献标识码：A 文章编号：1009-3044（2017）17-0240-02

1概述

最短路径问题在网络理论中应用得比较广泛，许多问题的优化，如厂区选址、火灾救援、交通运输、管道敷设、线路安排等都可转化为最短路径问题来处理。两点之间的最短路径就是两点间的所有路径中边的权值之和为最小的路径，而不是经过边的数目最少的路径。

2 Dijkstra算法

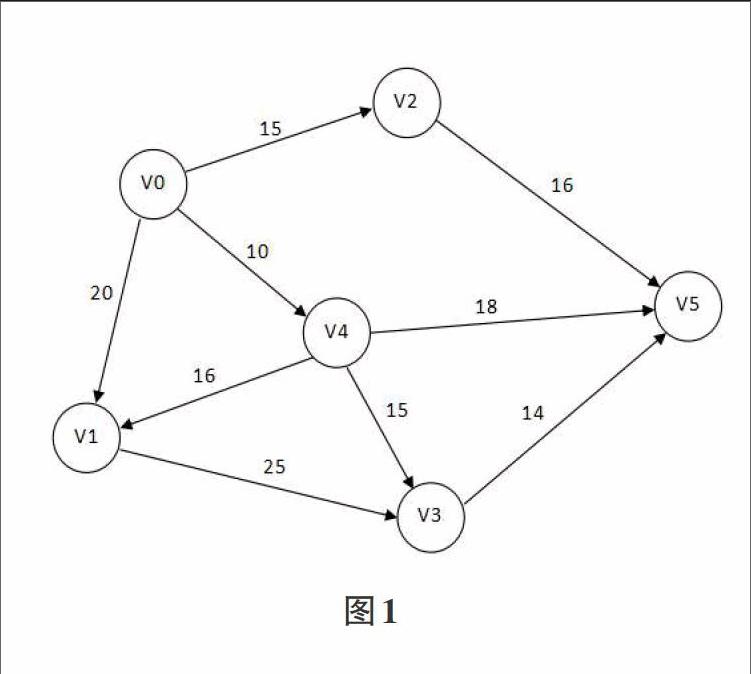
Dijkstra算法的前提条件是整个网络拓扑图，用图中的顶点表示地点，每一条边旁的数字称为权值，权值可以表示费用、距离等，这种算法只适用于求无负权网络图的最短路径；我们结合图1来介绍Dijkstra算法，图中我们要求源点V0到其他任意顶点的最短路径；

4最短路径算法在线路敷设中的应用

线路敷设是建筑工程施工设计中重要的部分，我们通过对敷设线路的优化来达到降低成本、增加可靠性的目的。线路设计的目标是在满足工程要求又符合规范的基础上减少用线缆量，其实这就是一个对线缆走向进行优化设计的问题，故如果我们将工程中需要接线的设备设为网络图的各顶点，设备到设备之间的路线设为无向图的边，这样线路的敷设问题就转化为了最短路径问题，进而我们就可以用最短路径算法找出网络图中最短又合理的路径来实现线路的优化。我们可以用以上的三种算法，根据其处理速度和准确性的比较来选择一种更优的算法。

5结束语

Dijkstra算法和Bellman-ford算法都是求图中源点到其他所有顶点之间最短路径算法，Dijkstra算法求的是单源以及无负权网络图的最短路径，Bellman-ford算法可以求有负权网络图的最短路径，这种算法可以判断是否有负权回路；Dijkstra算法在计算过程中，源点到顶点集S里各顶点的最短路径长度不再改变，改变的只是源点到不在顶点集S里各頂点的最短路径，而Bellman-ford算法在计算过程中，每次循环都要计算源点到各顶点的最短路径长度，直到Bellman-ford算法结束才确定。