基于输出调节及内模原理的无静差跟踪控制

侯 艳，张 武

（1.西安铁路职业技术学院 牵引动力系，陕西 西安 710014；2.西安科技大学 机械工程学院，陕西 西安 710054）

基于输出调节及内模原理的无静差跟踪控制

侯 艳1，张 武2

（1.西安铁路职业技术学院 牵引动力系，陕西 西安 710014；2.西安科技大学 机械工程学院，陕西 西安 710054）

针对工业过程普遍存在的无静差跟踪问题，本文在分析了目前常用的跟踪方法后，重点研究了基于输出调节及内模原理的无静差跟踪控制，分析了其理论方法，通过算例仿真验证了该方法的跟踪效果及特性，结果表明该方法具有很大的优越性。

输出调节；无静差；跟踪；内模原理

近年来，随着我国铁路运输业的发展，尤其是高速列车的迅速兴起，各关键技术在这一领域势必显示出其重要的作用，对于列车的安全有效控制关系着人身财产安全，关系着铁路运输的高效性能，具有举足轻重的意义，其中，高速列车的定点停车[1]、列车运行速度、制动压力的控制等需要高精度的跟踪控制技术，实际的控制系统通常会受到外部持续扰动力的影响，如列车运行过程中的空气阻力，机械旋转部件的周期扰动等，目前对于扰动抑制问题，主要的研究方法有：1）前馈反馈控制[2]，通过在系统的反馈控制回路中引入前馈通道，构成由前馈控制和反馈控制组成的复合控制。对于可量测扰动，可以通过前馈控制进行补偿。一般来说，对于主要扰动可以通过前馈控制进行全部或部分抑制，对于次要扰动可通过反馈控制进行补偿。但该方法只能针对可测量的扰动，具有一定的局限性。2）预测控制[3]，对于扰动未知但可预测的系统可以利用预测控制的滚动优化思想实时优化控制器参数。由于预测控制在每一时段都有一个相对于该时段的性能指标，因此预测控制不能实现全局意义下的最优。3）基于扰动观测器的控制[4]，该方法已经推广到非线性系统，可改善了系统性能，提高控制器对外部噪声及未建模动态的鲁棒性。但是该方法需要将原系统和外系统组合为一个新的增广系统，从而提高了系统的维数，当系统维数较高或子系统较多时计算负载较重。另外，该方法只是实现了对外部扰动的抑制和闭环系统的镇定，并未涉及最优化的思想[5]。

1 设计原理

文中所研究的基于输出调节及内模控制的方法原理是：控制系统的输出，以实现对外部信号的渐近跟踪和扰动抑制，同时保证闭环系统渐近稳定，在伺服补偿器中植入参考输入和扰动信号的共同不稳定模型（内模），依靠内模与不稳定振型的精确对消，从而达到无静差跟踪或扰动抑制的目的[6]。该方法的重要优点是，对除内模以外的受控系统和补偿器参数的变动具有很强的不敏感性。当受控系统和补偿器的参数产生摄动时，即使摄动的范围很大，只要闭环系统保持渐近稳定，控制系统仍然能够实现无静差[7]。基于内模原理的无静差控制的鲁棒性使其在过程控制领域得到了广泛的应用[8]。

2 设计步骤

考虑具有持续扰动的n维控制系统

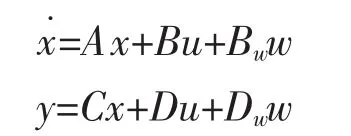
其中，x∈Rn是状态向量，u∈Rp是控制输入，Y∈Rq是输出向量，w∈Rq是外部扰动。假设（A，B）完全能控，（A，C）完全能观。假设控制系统的输出y（t）要跟踪的参考输入为 y0（t），跟踪误差

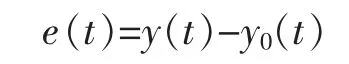
假设 y0（t）和 w（t）都不是渐近稳定的，并且其动态特性已知，其中参考输入y0（t）

由以下具有未知初始条件的模型产生：

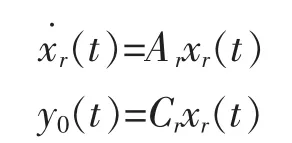
扰动信号由以下未知初始条件的模型产生：

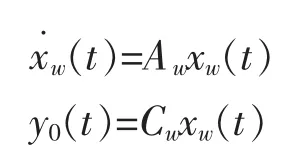
记 Φr（s）和 Φw（s）分别是 Ar和 Aw的最小多项式。要实现无静差控制，即

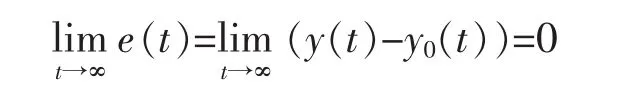
只需要考虑 y0（t）和 w（t）当时不趋于零的部分。表多项式办 Φr（s）和 Φw（s）的位于右半闭 s平面上的根因式的最小公倍式为

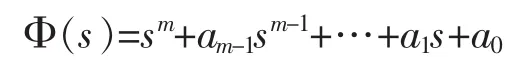
显然Φ（s）=0的所有根均具有非负实部，由Φ-1（s）Iq可导出 y0（t）和 w（t）当 t→∞ 时不趋于零的部分的共同模型，将跟踪误差e作为它的输入，则伺服补偿器可

构造为

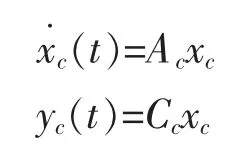
其中Ac∈Rmq*mq和Bc∈Rmq*q分别为下列矩阵

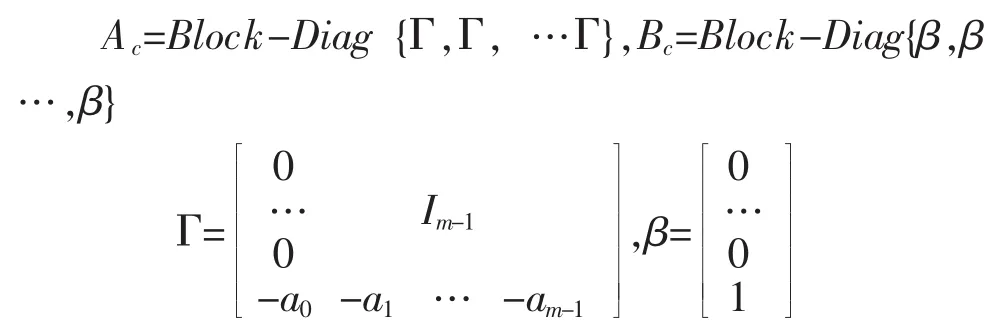
将伺服补偿器与原受控系统串联可得增广系统的状态方程为

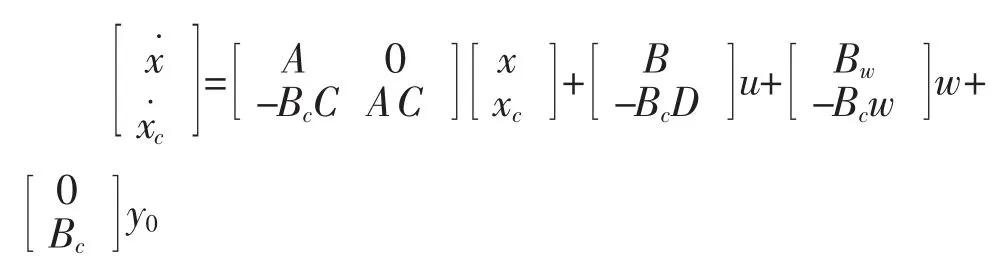
增广系统为完全能控，并能实现无静差控制的一个充分条件为：

1）受控系统的输入维数大于等于输出维数，即dim（u）>=dim（y）；

2）对参考输入和扰动信号共同不稳定代数方程Φ（s）=0 的每个根 λi，成立：

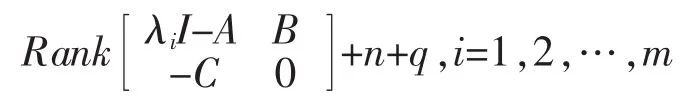
由此可见，无静差控制通过将伺服补偿器与原受控系统串联，从而实现了渐近跟踪和扰动抑制[9-11]。由于内模设计简单，而且能有效地抑制不可测扰动的影响，消除稳态误差，因此己成为一种设计与分析无静差控制系统的有力工具。应用内模原理必须要求外系统模型的动态特性已知，因此对于扰动不确定的情形，需要构造自适应内模来[12-15]。

3 算例仿真

给定一个连续时间线性时不变受控系统：

其中，n=4，p=1，q=1。 给定参考输入 y0（t）和扰动w（t）为阶跃函数。要求综合使系统实现无静差跟踪的镇定补偿器和伺服补偿器[16]。

1）离线计算定出镇定补偿器及伺服补偿器然后用matlab的simulink模块搭建仿真系统（图1），检验跟踪效果（图2）。

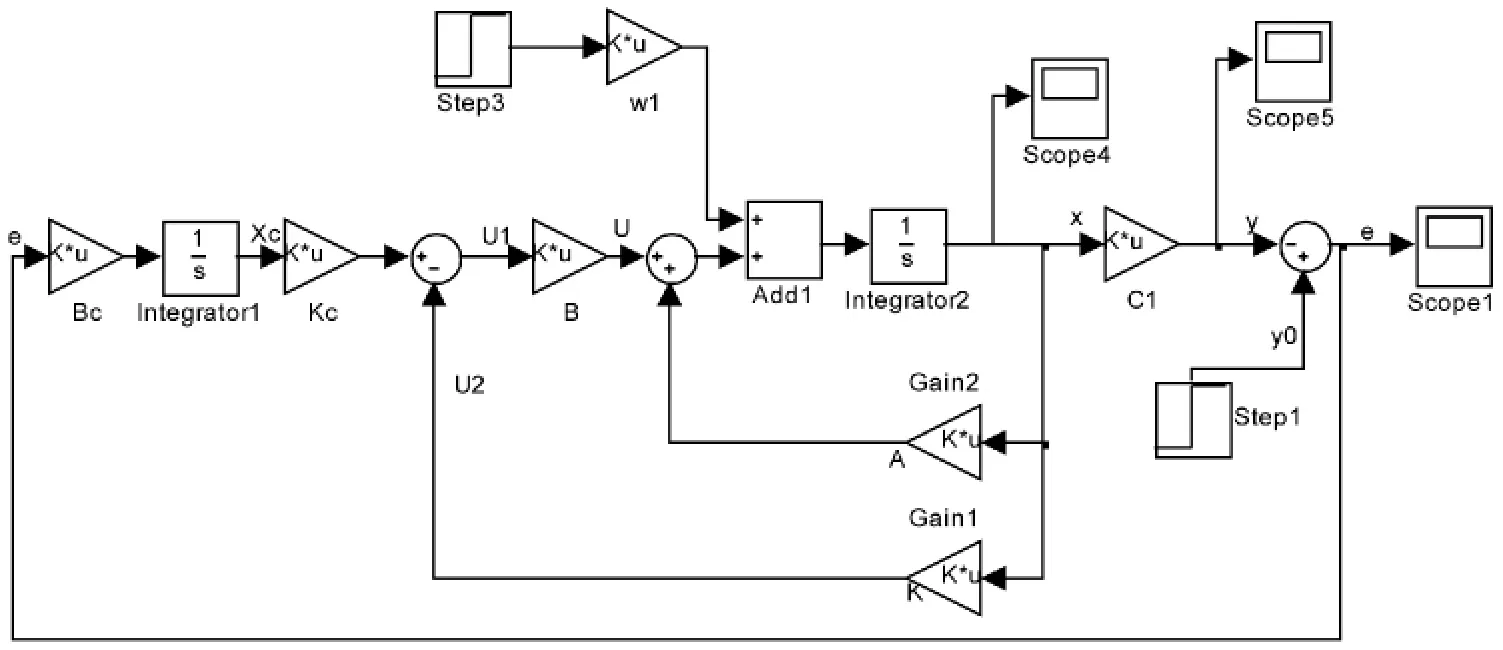
图1 simulink模块仿真系统图

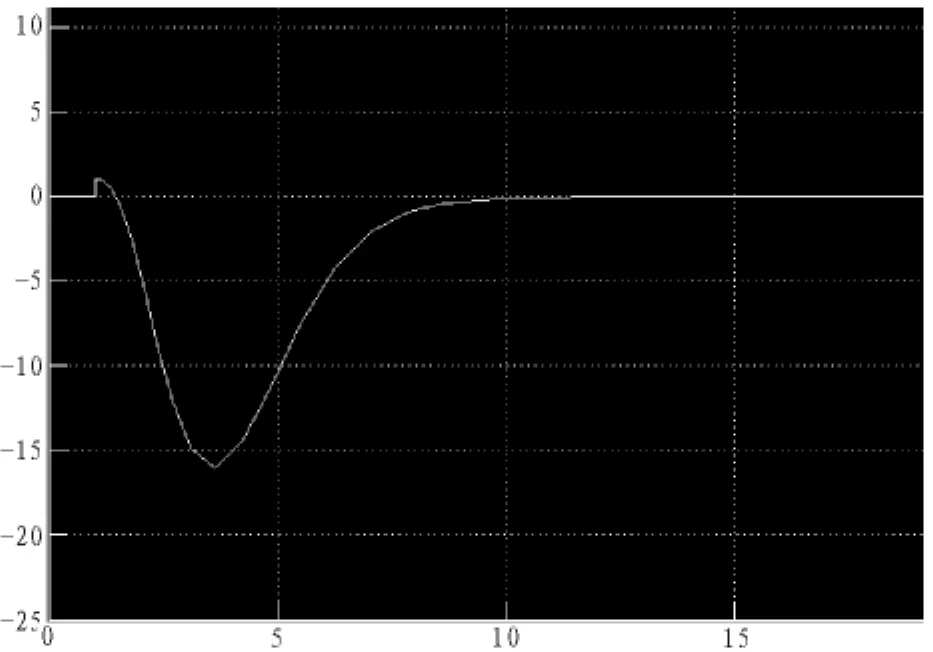
图2 跟踪曲线

由结果可以看出，一段调节时间过后，跟踪误差趋近于0，故表明用该方法得到的镇定补偿器和伺服补偿器有很好的跟踪效果。

2）扰动矩阵由【0 4 0 6】T变为【4 4 0 1】T时，跟踪效果如图3。

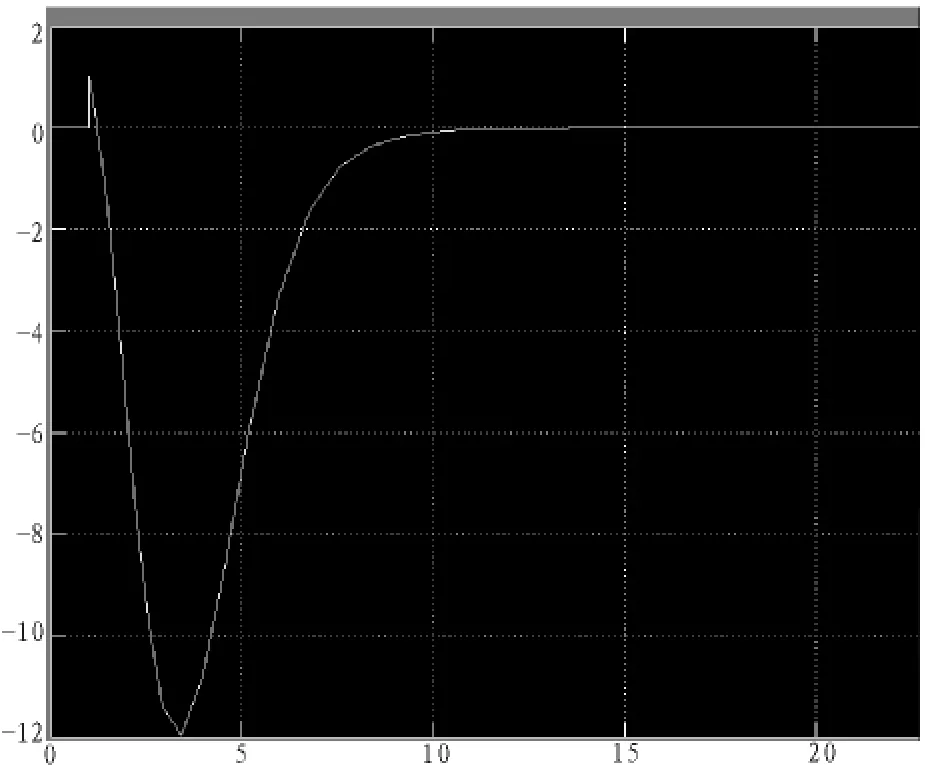
图3 扰动参数变化时的跟踪曲线

结果表明：在扰动参数发生较大变化的情况下，该方法依然能够实现无静差跟踪[17]。

3）当伺服补偿器的系数Kc由Kc=-0.4变为Kc=-1.2时，跟踪效果如图4。

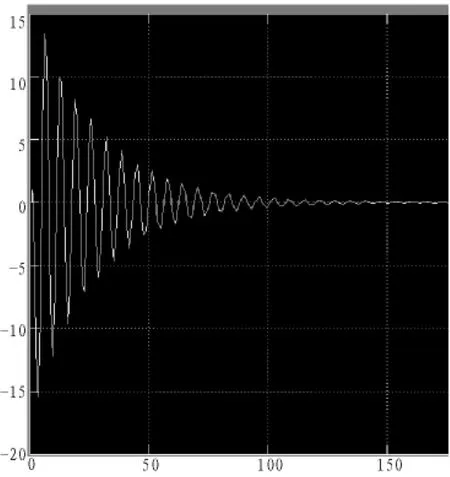
图4 内模参数变化不大时的跟踪曲线

由曲线可看出：系统经较长一段时间振动后实现无静差跟踪控制。

4）当伺服补偿器的系数Kc由Kc=-0.4变为Kc=-2时，跟踪效果如图5。

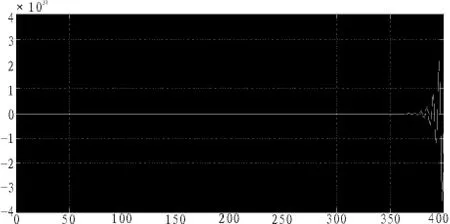
图5 内模参数变化较大时的跟踪曲线

将图5中间部分去除，两端局部放大后如图6。

由曲线可看出：由于伺服补偿器参数与理论计算值偏差较大，最终没能实现无静差跟踪控制。

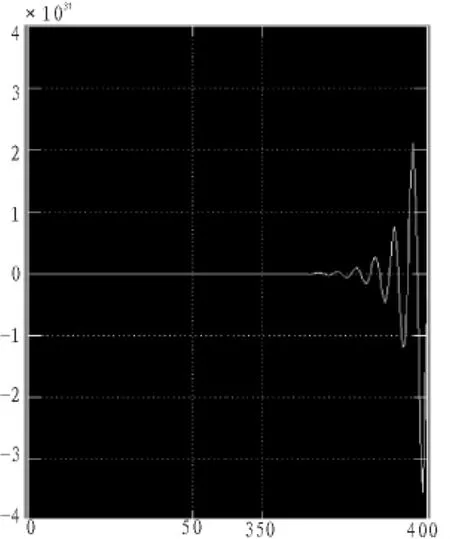
图6 对图5局部放大

4 结束语

本文在分析了目前对于扰动抑制问题主要的研究方法后，选择基于内模原理的控制方法进行研究，通过离线确定镇定补偿器和伺服补偿器，再进行在线仿真，表明其对内膜以外的参数变动具有较强的鲁棒性，但对内膜参数的变化几乎丧失鲁棒性。

[1]赵慧.基于RFID的定点停车系统的设计与实现[D].北京:北京交通大学，2015.

[2]罗绪涛，任亚飞，梁晓庚，等.基于前馈—反馈控制导弹自动驾驶仪鲁棒稳定性分析 [J].计算机测量与控制，2012.6，20（6）:1590-1591.

[3]徐祖华.模型预测控制理论及应用研究[D].浙江:浙江大学，2004.

[4]程毅.基于非线性高增益扰动观测器的控制系统设计[D].广东：华南理工大学，2011.5.

[5]谢巍，何忠亮.采用改进型扰动观测器的控制方法[J].控制理论与应用，2010.6，27（2）:695-700.

[6]郑大钟.线性系统理论[M].北京：清华大学出版社，2005.

[7]王孝武.现代控制理论基础 [M].北京：机械工业出版社，2009.1.

[8]庄文许.基于内模原理的某舰载火箭炮操瞄控制系统研究[D].南京：南京理工大学，2013.

[9]程代展；董亚丽 输出调节和内膜原理 [J].自动化学报，2003，20（4）:1-4.

[10]雷靖.线性系统的输出反馈次优扰动抑制：内模原理方法[J].云南大学学报，2012，34（4）:408-411.

[11]雷靖.控制时滞与测量时滞采样系统的最优扰动抑制[J]云南民族大学学报：自然科学版，2012，21（1）:45-47.

[12]唐功友，赵翀，雷靖.含有控制时滞系统的输出反馈扰动抑制[J]中国海洋大学学报：自然科学版，2007，37（4）:667-670.

[13]平续斌，丁宝苍，韩崇昭.动态输出反馈鲁棒模型预测控制[J].自动化学报， 2012，24（1）:31-33.

[14]LEI J.Suboptimal vibration control for nonlinear suspension systems based on in-vehicle networks.Proceedings of 2011 International Conference on System Science and Engineering， 2011，46 （31）:22-24.

[15]李生明.内模原理的伺服系统最优控制[J].清远职业技术学院学报， 2012，5（6）:38-40.

[16]李 莹，潘宏亮，秦飞，等.基于EASY5的液发系统建模与仿真可行性研究[J].火箭推进，2015（1）：70.

[17]李丹，王旭红，李向前，等.基于控制参数调整的容性逆变器容性深度研究 [J].供用电，2015（9）：63-68.

Non static error tracking control based on output regulation and internal model principle

HOU Yan1，ZHANG Wu2
（1.Department of Railway Power Traction，Xi'an Railway Vocational and Technical College， Xi’an 710014， China ；2.School of Mechanical Engineering， Xi’an University of Science and Technology，Xi’an 710054，China）

Aiming at the problem of non static error tracking in industrial process，In this paper， after analyzing of the current commonly used tracking methods，the paper focuses on the control of non static error based on the principle of output regulation and internal model.Its theoretical method is analyzed.The tracking results and characteristics of the proposed method are verified by a numerical example.The results show that the method is of great advantage.

output regulation； non static error； track； internal model principle

TN99

A

1674－6236（2017）12-0053-04

2016-06-28稿件编号：201606218

国家自然科学基金资助项目（51505373）；陕西省教育厅科研计划项目资助（15JK1490）

侯 艳（1988—），女，陕西渭南人，硕士，助教。研究方向：自动化与检测传感技术。