层层质疑，彰显数学学科的育人价值

林朝冰

[摘要]教书最终是为了育人，拓展学科的育人价值是培养新一代高素质人材的需要，当数学学科的育人价值与质疑精神遇时，将碰撞出怎样的火花？本文通过两个实例来探讨如何通过层层质疑的方法探究数学概念的形成过程及数学问题的本质，从而彰显数学学科的育人价值。

[关键词]层层质疑 学科的育人价值 概念的形成过程 问题的本质

[中图分类号]G633.6 [文献标识码]A [文章编号]2095-3089（2017）12-0078-02

数学学科的育人价值包括很多方面，其中以数学概念的形成过程、某类数学问题的本质的挖掘过程作为育人资源，可以使学生了解数学概念的来龙去脉，感受数学发现的基本思想和方法，并利用学习到的数学的思想和方法逐渐建立起自己的发现方法和理性思维策略，形成基本的数学素养。这是数学教学所特有的教育价值。质疑是探索知识，发现问题的开始，是获得真知的必要步骤，数学课堂教学是一个师生共同设疑，释疑的过程。通过层层质疑的方法探究数学概念的形成过程，数学问题的本质，更能彰显数学教学的育人价值。本文通过两个实例来探讨如何通过层层质疑的方法探究数学概念的形成过程及数学问题的本质，从而彰显数学教学的育人价值。

一、通过层层质疑，探究概念的形成过程

正确理解概念是数学学习的基础，缺乏产生过程的概念教学将导致学生对数学概念的认识缺乏整体性。下面以导数的概念教学为例，说明如何通过层层质疑的方法探究概念的形成过程。

1.设问题情境，引发自主探究

高速公路的某处，限速100km/h，一辆汽车以120km/h的速度到达距测速摄像头50米处，驾驶员发现摄像头后立即减速，正好以100km/h的速度通过测速点，问该辆汽车是否超速？

设计意图：让学生产生质疑测速摄像头所测到的“速度”是平均速度还是瞬时速度？瞬时速度是如何得到的？平均速度是怎样计算的？（ ），瞬时速度又是怎样计算的？（ ），通过层层质疑和探究体会到瞬时速度是平均速度的极限。

2.曲线的切线问题探究

问题一、圆与圆锥曲线的切线是如何定义的？

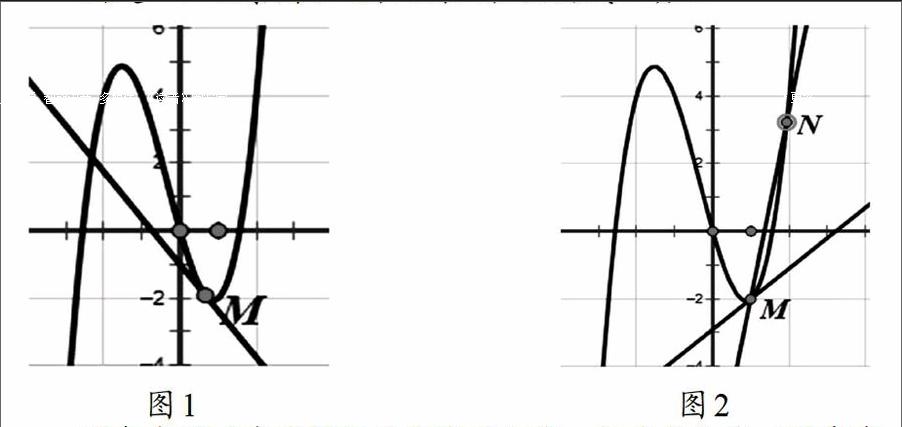
问题二、观察图1（用几何画板使切线运动）。

图象中的动直线始终是曲线的切线，切线与曲线可以有多个公共点，而且曲线图象的也不总在切线的一侧，学生开始质疑以前学的切线的定义，接下来引导学生寻找新的切线的定义方法。

问题三、图2中割线MN与点M处的切线有何关系？

引导学生通过运动得到切线，体会由“割”变“切”的过程，从而体会逼近和极限的数学思想。并得出曲线的切线的定义，切线是割线MN当N点沿曲线运动到点M时的极限位置。得出切线的定义后，又引导学生质疑：

问题四、切线的斜率应该如何求？

回顾问题二，引导学生探究，切线是由割线运动的极限位置，那么切线的斜率是否可通过割线的斜率求得？

问题五、平均速度及割线的斜率本质是什么？

通过问题五使学生体会到导数的本质是平均变化率的极限，从而实现了思维的飞跃。

本例通过引导学生层层质疑，体会到数学来源于生活，体会了由特殊到一般的抽象过程，体会了逼近和极限的数学思想，使学生的思维得到了升华，从而彰显数学学科的育人价值。

二、通过层层质疑，探究数学问题的本质

透过问题的现象，探究问题的本质，通过层层质疑，使学生在不断发现和提出问题、分析和解决问题的过程中，产生主动探究的欲望，培养思维能力和创新能力，从而提高学生的解题能力；同时产生丰富的情感体验，彰显数学学科在培养学生信心、习惯、意志、态度和价值观等情感的育人价值。下面以“几何体外接球的体积”为例说明如何通过层层质疑的方法探究数学问题的本质。例、一个正方体的顶点都在球面上，它的棱长为a，求球的体积。

此例比较简单，学生完成后教师提出问题：

问题一、能不能把正方体换成其它几何体？

学生得出以下两个问题：

（1）一个正六棱柱的底面边长为a，高为h，顶点都在球面上，求球的体积。

（2）一个正三棱柱的底面边长为a，高为h，顶点都在球面上，求球的体积。

问题（1）学生模仿例一能轻松解决，然而对于问题（2）学生将三棱柱补形成四棱柱来解决。

问题二、你能确定补形后的四棱柱的顶点都在球面上？

学生开始反思，“要使四棱柱的顶点都在球面上，底面四边形必须是圆内接四边形！”

问题三、球心与底面外接圆的圆心有什么位置关系？

学生自主研究并容易得出以下结论，“球心到底面的正投影就是与底面外接圆的圆心”

小结反思：“本题的关键是什么？”（球心的位置）。“本题的本质是什么？”（球的半径与正方体棱长的关系）。

问题四、如何找出球心的位置？

经过自主探究学生得出寻找球心的方法：先找到底面多边形的外心，再垂直向上寻找球心。

学生探究问题（2）后，得出结论“球心位于底面正三角形中心垂直向上距底面处”。

问题五、球心到底面的距离是否一定是高h的一半？

问题六、你能再次改变球内接几何体的形状吗？

得出以下问题：

（3）三棱锥V-ABC中，AB=AC=a，VA底面ABC，顶点都在球面上，求球的体积。

（4）三棱锥V-ABC中，AB=AC=BC=a，VA底面ABC，顶点都在球面上，求球的体积。

（5）正三棱锥V-ABC中，AB=AC=BC=a，高为h，顶点都在球面上，求球的体积。

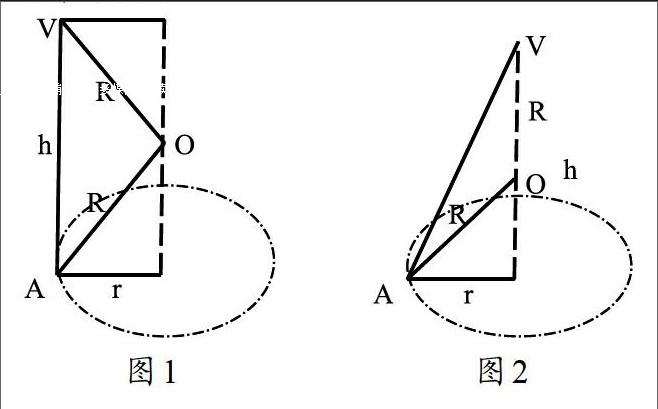
问题（3）、（4）的结论是：球心到底面的距离是否一定是高h的一半。问题（5）的结论却不同。学生自然会问为什么？引导学生观察下图：

问题（3）、（4）中，顶点V在底面的投影正好是底面顶点如图1示，因为球心O到点v的距离与到点A的距离相等，所以球心到底面的距离是高h的一半。问题（5）中，顶点V在底面的投影正好是底面多边形外接圆的圆心如图2示，因为球心O到点V的距离与到点A的距离相等，所以球心到底面的距离不等于高h的一半。紧接着引导学生产生新问题：

问题七、几何体外接球的半径R与几何体的高h及底面外接圆的半径有什么关系？

结合图1、图2学出容易得出以下结论：（i）当锥体侧棱与底面垂直时，R²=r²+2h²，（ii）当锥体侧棱与底面不垂直，顶点v在底面的投影正好是底面多边形外接圆的圆心时，R²=r²+（h-R）²

问题八、已知A，B，C三点在球面上，AB=AC=2，球心到面ABC的距离为1，求球的体积。

本例通过引导学生改变几何体的形状，层层质疑，探究出此类问题的本质及解决办法，学生处在一种愉快的探索知识的过程中，学习和体验到发现和探究问题的基本方法，不仅使学生所学知识纵向加深，横向沟通，使学生的发散思维和创新思维得到了培养，提高学生分析问题和解决问题的能力，还使学生得到了丰富的情感体验，彰显了数学学科的育人价值。

三、结语

数学学科的育人价值不能停留在教学数学知识上，数学概念的产生和发现的过程，数学的质疑精神，思维方式，思想方法以及在數学探究过程的情感体验等等都具有丰富的育人价值，广大的数学教师应将育人的意识，贯穿于自己的教育教学的始终，落实在教学活动实际中。