FFT算法在脑电波信号谱密度分析中的应用于实现

张时超

摘要：该文分为四大部分，第一部分介绍了脑电波信号的几种处理方法，包括时频与神经网络等方法。第二部分重点介绍了时频分析中快速傅里叶变换（FFT）的原理及其优点，并阐述了选择其进行脑电波分析的原因。在第三部分中，实现了该文的主要目的，编写了使用FFT方法并基于matlab的程序，用来分析仿真脑电波的数据。包括代码的注释以及实验结果分析截图。第四部分通过了谱分析的结果参照相关文献讨论现象。

关键词：脑电波信号；时频分析；快速傅里叶变换（FFT）；Madab

中图分类号：TP391 文献标识码：A 文章编号：1009-3044（2017）13-0225-03

脑电波信号（eeg signals）是一种非常复杂的随机信号，是大脑组织电活动和大脑功能状态的综合反映。由于不同的思维状态和病理情况在大脑的皮层位置的反映不同，我们会得到不同反映的脑电图（EEG）。在医学检测方面，脑电信号的分析结果可以为处理特别的脑系疾病提供相对应的依据以及针对治疗方案。同时，随着计算机应用技术的成熟，脑与计算机接口技术的发展，我们可以通过计算机来对脑电波进行处理从而分析人们对特定感觉产生的不同的脑电波。脑电波信号是一种非平稳且随机的特殊信号，所以提取脑电波信号中有用处的信息就成为了极为有前途却非常有难度的研究课题。

1脑电波分析方法概述

1.1时频分析

1）时域分析：由于时域分析的直观性非常强而且物理意义明确，所以从这种方法提取特征是早期最为主要的方法。而却有些十分重要的信息在时域上反应明显，比如棘慢波反映了癫痫的信息，还有反映睡眠信息的梭形波等瞬态波形，由此可见，时域分析在目前脑电波定量化分析中占有非常重要的地位。但是时域方法的缺点在于大脑各个区域的脑电波情况并不能得到直接的反映。

2）频域分析：功率谱分析是频域分析的主要手段。它的主要作用在于把脑电波幅度相對于时间变化的关系转化为脑电波功率相对于频率变化的谱图。时域分析方法对如幅值，波形的持续时间等脑电波信号波性特征参数进行识别，它没有考虑到信号在频率上的分辨率，而是仅仅给出信号在时间上的分辨率。我们假设脑电波信号的特性是平稳的，只有在这样的假设基础上，我们才可以使用频域分析方法，所以说他的缺点就是只考虑了信号的频域信息而忽略了其在时间上的分辨率。

3）时频分析（JTFA）即为时频联合域分析（Joint Time-Fre-quency Analysis）的简称。我们知道，脑电波信号是时时变化且非平稳的信号，在不同时刻都有不同的频率成分，所以说单纯的时域和频域都不能准确的表达信号。而且在脑电图（eeg）中许多病变都是以瞬态的形式表现的，那么我们认为，只有把时间和频率结合起来，这样才能取得更为优秀的结果。所以说时频分析方法在时域和频域都同时具有非常良好的局部化分析而且它还具有其他一些很重要的性质，所以在脑电波信号分析中收到了相当的重视。最简单的时频方法就是短时距傅立叶变换（short-time Fourier transform，STFT）。时频分析也有它的缺点，就是必须在时间分辨率和频率分辨率之间进行权衡，本文会在下面简单介绍几种常用的时频分析方法，包括快速傅里叶变换（FFT），连续小波变换，Wigner-Ville分布。

2快速傅里叶变换（FFT）

FFT是离散傅里叶变换（DFT）的更高效更快速的计算方法。FFF是根据DFT的奇偶虚实等特性，对它的算法进行改进而获得的。FFT在本质上并没有对离散傅里叶变换的理论基础有新的改革，但是它在计算机领域中对于DFT的应用可以说是一个重大的飞跃。当在使用FFT算法时，计算机对离散傅里叶变换所需要进行的乘法次数大大减少，特别是被变换的抽样点数越多，节省的时间复杂度越明显。我们会在下一章中重点介绍FFT算法。

傅里叶变换在信号处理中具有非常重要的作用，是进行时频分析的主要手段，但是基于离散时间的傅里叶变换的时间复杂度非常大，在傅里叶变换的理论中，对一个有限长度为Ⅳ的离散信号，对其做傅里叶变换，所以说当N很大时它实现时消耗时间的是一个非常大的数量级，所以它的实现难度是非常大的，同时也严重制约了DFT在信号分析中的应用。正是因为DFT算法时间复杂度的考虑，提出了一种快速且有效的算法来实现目的，这就是快速傅里叶变换（FFT）。

2.1FFT基本思想

快速傅里叶变换基本思想是把最初的N个采样点的序列，进行相互的组合，变成了一些短序列。由于在离散傅里叶变换计算公式中指数因子的周期性和对称性，我们就分别的求出了这些短序列的相应的DFT并且我们把他们进行适当的组合，这样就可以减少重复的计算和减少乘法计算的次数从而达到结构优化的目标。

2.2FFT优点及选用此方法原因

首先我们知道FFT是DFT的快速算法，DFT的时间复杂度为0（N*21，经过FFT对原先Ⅳ个采样点的分组后进行DFT在进行组合，达到优化的目的，这样FFT的时间复杂度就是0（NlogN）。这样，就从数字角度上解释了为什么采样点Ⅳ越多，FFT在计算机上节省的时间就越多。并且由于其在计算机计算方面的优越性，我们选用此种算法结合matlab来实现此次脑电波谱密度分析程序的研究。

3基于MATLAB的脑电波谱密度分析程序编写与实现

3.1数据来源分析

采集EEG的位置是后脑的0z电极处，采样率600Hz，刺激器频率15Hz。

如图，刺激器每一个小节（trial）闪烁3秒，停2秒，之后开始第二小节，总共30个小节。

以数据集load ssvep_fatigue_1_sl为例，在MATLAB中load数据集后我们可以得到一个名叫savedata的矩阵2*54000，其中第一行就是0z的EEG，第二行就是同步信号，采样率600，所以54000/600=90 sec=30个trials*3 sec，之间没有任何无用数据。

3.2代码重点部分解释

以下matlab代码为载人模拟脑电波数据集ssvep_fatigue_1_s4_20121024，并创建名为data的矩阵存储数据集。

load ssvep_fatigue_1_s4_20121024；

以下为几种变量，依次为信号长度，采样频率，采样点数，采样点数越大，分辨的频率越精确，NFFT>=L，超出的部分信号补为0，频率，幅值。

可以得到以个1*30的矩阵，你就可以找到每个trial数据的第一个点的位置，然后把每个trial的数据分别提取出来做FFT，最后得到每个波段amplitude的平均值，作为这个波段的index，30个trials，每个index就有30个点，以下为代码。

heads=find（savedata（2，：）>0）；%heads数组的每个元素，就代表着每个trial的第一个点

4实验结果及分析

4.1程序运行结果截图

4.2实验结果图说明

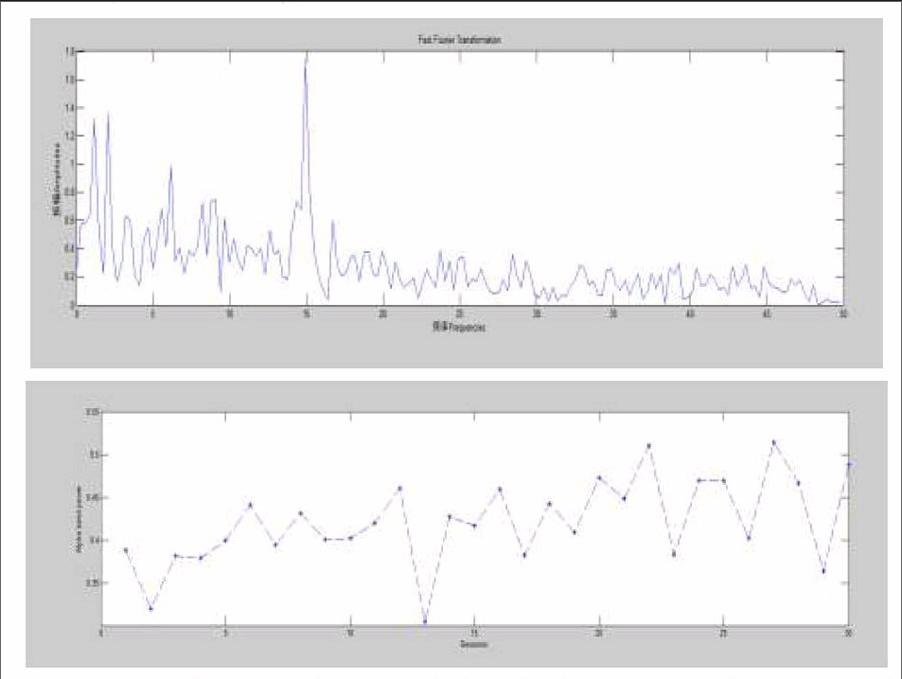
结果图上半部分图是脑电波信号数据进行基于m变换的谱密度分析之后得到的频谱图，横坐标为频率，横坐标为对应振幅。下半部分图横坐标是三十个sessions，纵坐标为当脑电波频率为8到12HZ（也就是阿尔法波）时每个session对应的阿尔法波的平均振幅，图中有三十个离散的点。

4.3实验结果分析

从上面的频谱图中我们可以得出脑电波的频率和幅度之间的关系，从而通过程序筛选出频率为8-15HZ对应的平均振幅在时间上的变化。

我们以图为例，分析图中反应结果：

经过m变换后，我们得到了脑电波频率与对应的振幅，首先，对脑电波的频率我们有一定的先验知识：

8波：深度睡眠脑波状态（范围0.5-3HZ）。

θ波：深度放松、无压力的潜意識状态（范围4-8HZ）。

α波：频率每秒8～13Hz，振幅20～100μv。正常安静、清醒闭目时出现。睁开眼睛或接受其他刺激时，立即消失而呈现快波，称为α波阻断。

β波：紧张、压力、脑疲劳时的脑波状态（范围14HZ以上）。

从图，我们观测到了阿尔法波在不同时间的平均振幅，从而判断出被观测者在不同时间中阿尔法波的振幅，这在对观测者的精神状态分析和病理判断起到了辅助作用。

5总结与展望

脑电波信号是非平稳且随机的非线性的复杂信号，他的处理和分析在临床诊断上起到了极为关键的作用。也因为信号本身的特点，使分析处理成为一项非常有难度的课题。近些年，由于计算机技术的日新月异，我们相信，未来的脑电波分析手段和计算机技术的有机结合是非常有前景的方向，而计算机对信号处理的精确度和效率也有极为可观的改善。