基于多模式接单的出租车资源配置方法

陈金鹿　朱海钫　李俊辉　许文德

摘要：提出了一种基于多模式接单的出租车资源配置方法。从缓解乘客“打车难”、出租车司机趴活难的角度出发，首先建立基于多元线性拟合的司机服务质量评分模型；然后在司机自由抢单环节建立基于服务质量的查单时间滞后函数；最后在后台指派任务时综合考虑司机的服务质量和到乘客位置的最短路径，建立基于排队论的最优化匹配算法。仿真结果表明：该方法不仅有效缓解了乘客打车难问题，而且明显降低了司机空驾率和乘客候车时间。

关键词：多模式接单；多元回归；Dijkstra算法；排队论；最优化

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2017）13-0086-03

近年来，各互联网打车公司在出租车资源配置问题上主要采取补贴的方式，从而提高司机和乘客使用打车软件的积极性。企鹅智库的调研结果表明，从2016年互联网公司取消补贴政策开始，只有50%的乘客愿意继续使用打车软件，这也意味着出租车资源的配置已经回归到市场的自动调节。为了合理地配置出租车资源，许多学者提出了实时预测出租车供求关系的资源配置方式，例如，单欣等运用多元统计、相关分析和灵敏度分析等方法，得到了不同时空出租车资源的供求匹配模型和劣单拒载模型；安晓丹等给予多指标体系，建立阀值函数，给出了不同时空下出租车资源的供求匹配等级；姜浩等运用模糊综合评价和灰色关联度分析等方法，对比了打车软件兴起前后的供求匹配度，并得出了打车软件对缓解打车难效果不明显的结论；黄瑞等统计分析、变异系数等方法建立多指标综合评价模型，结果表明北京市早晚高峰期存在打车难现象；赵文杰等运用C类均值聚类、IDT理论和隶属度函数等方法，分析了各城市的出租车资源在时间上的分布情况。上述研究均以在不同时空下的出租车供求状况为研究对象，忽略了司机历史服务质量对供求匹配率的影响，而且综合评价模型的结果只给出了大幅度区域内早中晚的供求匹配等级，偏差较大；另外C类均值聚类模型把出租车资源的成功匹配度划分为三类，这导致得出来的结论缺乏实时配置的作用。对于这些问题，本文以最优化匹配乘客和出租车为目标，综合考虑出租车司机的历史服务质量，运用二次函数、Dijkstra算法、排队论等方法对司机自由抢单和后台指派任务两种先后顺序的接单模式进行实时调度，实时获取每位乘客的候车时间、任意区域内的打车成功率及司机的空驾率，为打车软件提供了一种新的司机端接单模式。

1问题分析

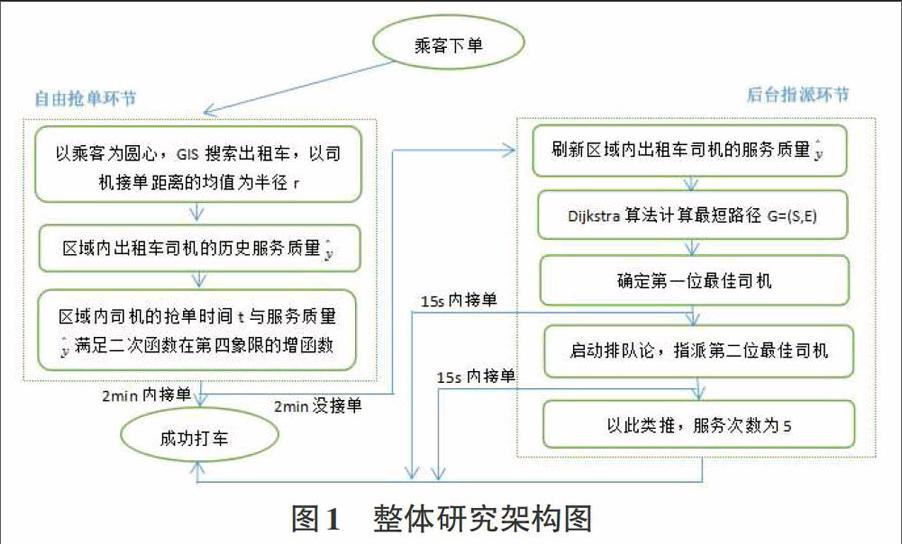
出租车资源的动态匹配问题，实际上是如何根据现有的互联网打车软件对乘客的订单进行快速匹配出租车的问题。目前，滴滴司机端2.0及以上版本已经推出了司机自由切换抢单和任务指派的两种接单模式：订单优先分配给开启指派模式的司机，若连续三位开启指派模式的司机均不接单，再推送给开启抢单模式的司机，而司机在指派模式的成交率将影响后续收到订单的数量。根据调研，我们发现高达30%的司机会拒绝指派的订单，也有24%的乘客由于指派的出租车过远而取消订单。由此可见，这种新模式难以从根本上缓解打车难问题的主要原因在于没有建立对司机和乘客的奖惩制度和控制接单模式的时间。于是本文首先建立了每位司机的历史服务质量评分模型，引用文献中司机意愿接单半径的概念，在以乘客为圆心、以接单距离为半径的圆区域内的司机才有机会看到乘客的订单，而且司机查看订单的时间和历史服务质量服从二次函数在第四象限的增曲线；若2min内无司机接单，则后台进入任务指派模式，运用Dijkstra算法可计算出区域内每辆出租车到乘客位置的最短路径，综合考虑司机服务质量，通过熵的方式即可匹配出最佳出租车，若收到指派信息的司机在15秒内没接单，则启动排队论，匹配第二位最佳司机，综合考虑司机的拒单时间及乘客的等车时间，本文合理设置指派司机的次数为5次。

2司机历史服务质量评分模型

每位司机的历史服务质量将影响到抢单和任务指派的优先级，因此建立完善的评价系统十分重要。结合文献，我们认为每位司机的服务质量主要由以下三个方面构成：后台指派任务时的接单率，被投诉值和乘客的评分均值。

2.1每位司机在后台任务指派中的接单率模型

（1）

其中，X₁为某位司机收到后台派单的总次数，X₁为该司机拒绝指派的次数。

2.2乘客对每位司机的服务质量评分模型

我们提出了完善的评分系统，每位乘客司机打分可获得积分，积分可用于兑换打车优惠券。每位司机对应了多位乘客，假设每位乘客对某位司机评价分值为X_2i，分数值域为[0.1，0.2，…，1.0]，数值越大，则表示该次服务越满意，因此，每位司机的平均服务质量评分模型为：

（2）

其中X_2i为每位乘客对某位司机的评分，n为评价该司机的乘客数。2.3每位司机被投诉风险模型

若司机违反城市交通规章制度，乘客有权利投诉该司机。投诉分值越高，则表示司机被投诉风险越低，1.0表示无被投诉记录

（3）

其中X_3i为每位乘客對某位司机的投诉，n为投诉该司机的乘客数。

2.4每位司机的综合历史服务质量模型

对以上三个评价模型进行多重线性拟合，即可得到每位司机的综合历史服务质量模型：

（4）

其中X₃为每位司机的综合历史服务质量模型，并且每改变一个影响因素将自动刷新一次服务质量。

通过大量的随机调研，最终求得回归模型如下：

3司机的平均意愿接单半径

为研究出租车的平均载客意愿半径，我们以广州市增城区为例，采用追踪法，对每辆车进行编号，采集了某时刻下的200辆出租车的载客意愿距离，并统计出在所有出租车司机使用打车软件接单时司机与乘客的位置，对所有数据进行加权平均，即可估算出司机的平均意愿接单半径为r=1.5km，司机的最大接单承受距离为r_max=3km，设出租车的数量为N，

一般情况下，在以i为半径的圆内，出租车的数量1≤N，若该区域内N=0，则后台将适当扩大半径进行搜索出租车，直到1≤N，同时也要保证半径小于3km。

综上，接单半径模型为：当1≤N1≤N，则r=rr=r，当N=0N=0，r≤r≤r_maxr≤r≤r_max。

4司机自由抢单模式一司机抢单时间滞后函数

以每位下单的乘客为圆心，以接单距离rr为半径的圆区域C内的乘客均可看到下单信息。但是由于司机的服务质量不同导致收到下单通知的时间不同。即，司机的服务质量越高，在自由抢单环节，越早看到订单信息。结合文献，不同历史服务质量的司机在查收订单时满足二次函数在第四象限上递增的分支：

其中最小是20表示信誉为0的司机，查单时间滞后20s，最大值0表示信誉为1的司机在乘客下单后可立即查收订单。通过区分司机的查单时间，可以有效改善司机“挑单”的现象，提高成功匹配率。

5后台指派模式

5.1最短路径模型

若在抢单总时长t₀=2mm内，无司机接单，后台将进行指派任务，该过程综合考虑了区域内的司机服务质量和司机实时位置到乘客的最短路径，从而选择最佳出租车，并指派该司机前往服务，若指定的司机在响应时间t₀=15s内拒单或超时，则启动排队算法，安排次佳出租车前往服务。

圆c内每辆出租车到乘客的位置均有最短路径，后台会根据乘客与出租车的位置计算出最短路径。

文献中指出Dijkstra算法可用于快速计算出租车与乘客之间的最短路径。设G=（S，E）是一个带有权的有向图，把所有顶点V分为两组，M是已求出最短路径的顶点集合，初始状态下M中只有源点s，随后每求出一条路径，S₁，S₁，…，S_K都加入M中，算法结束。N是未确定最短路径的顶点集合，按最短路径长度的递增次序依次将N里的顶点放进M，在向M中添加顶点时，始终保证从源点S到M中各点的距离为最短距离。本文把道路实际长度作为权值进行优化线路。

5.2最佳司机模型

设圆c内某辆出租车到乘客的最短路径为L（单位km），而该司机服务等级为y，

综合以上两个因素，针对某个订单，我们就可以定义范围内每位司机的择优模型：

（6）

对于从未接过单的新司机，后台会适当增大最短路径的距离，从而降低指派的要求，通过市场调研，发现对于从未接单的司机，若在最短路径的基础上增大0.2km，新司机将由更大的机会接到第一单。因此，新司机的指派模型为：

（7）

6验证模型

6.1乘客等车时间模型

后台选择最佳出租车后，即把乘客的相关信息发送给该司机，若司机在15秒内接单，则该单匹配成功。若司机超时或15秒内拒单，则后台启动排队论，把单发送给下一位最佳司机，若连续5位司机拒绝接单，则后台自动取消该订单。假定在该过程所有的出租车的位置不变，后台在运行程序的时间忽略不计。

7模型仿真

为了更明显地模拟验证本文模型的有效性，根据文献，我们引入了“帧数”的概念，建立一个包含4条井字型街道的二维图像，在每条街道上，随机产生25辆空出租车和30位需要打车的乘客作为研究对象（假定所有的乘客和出租车司机均使用打车软件）。考虑的出租车活动半径均为R=1.5km，对于每一辆空出租车，当在其活动半径内存在还未匹配成功的乘客，则认为该乘客可成功打到车。若活动半径内有多个订单，则认为出租车只会接下最近的订单。

模拟结果如表1所示：

分析可得，通过本研究提出的匹配算法，乘客的打车难度系数比使用滴滴打车降低了20%，由此可见，本研究对缓解打车难度有显著的帮助，同时乘客的候车时间和出租车的空驾率均明显减低了。

8结束语

本文通过提出两种接单模式的合理调制，综合考虑了出租车司机的历史服务质量，在自由抢单过程提出了类二次函数的司机查收订单滞后时间函数，在后台指派任务过程，考虑了到乘客位置的最短路径，并通过控制排队论的服务次数，求得乘客候车时间模型。最后通过模拟仿真出租车的实际运作场景，证明了本文模型在很大程度上緩解了打车难问题，同时还缩短了乘客等车时间。