四旋翼飞行器的自抗扰控制方法研究

戴启浩+马国梁

摘要：【目的】为了检验自抗扰控制方法是否可以应用在四旋翼飞行器飞行控制系统。【方法】介绍了自抗扰控制器的原理以及基本组成。针对四旋翼飞行器低速飞行或悬停状态， 提出了一种基于自抗扰控制器的控制系统设计方法并在仿真平台上进行稳定控制、高度控制实验， 以及与PID控制系统进行对比分析实验。【结果】仿真结果表明：基于自抗扰的四旋翼飞行器控制系统具有较好的动态品质、稳态精度以及较强的鲁棒性，【结论】本文所设计自抗扰控制器可应用在四旋翼飞行控制系统。

关键词： 四旋翼飞行器；自抗扰控制；扩张状态观测器； PID控制

中图分类号：TP29 文献标识码：A

Abstract：【目的】To test whether the ADRC can be applied in quadrotor flight control system。【方法和过程】This paper introduces the principle of ADRC and basic components.In view of the quadrotor flying at low speed or hover state，the writer puts forward a method of control system based on ADRC and on the simulation platform for stability control experiments，height control experiments，and analysis of the experiment compared with the PID control system .【結果】The simulation results show that： the control system based on ADRC has good dynamic quality ，steady precision and strong robustness.【结论】The adrc designed in this paper can be used in quadrotor flight control system.

Key words：quadrotor；ADRC；ESO；PID

1引言

四旋翼飞行器是一种比较热门的新型旋翼无人机，由于其具有机械结构简单、可垂直起降、成本较低等特点，因此被大量应用于侦查，巡线，喷洒农药等领域。飞行控制系统设计是整个四旋翼飞行器控制系统的核心，常用的方法有PID[1]，反步法[2]、自适应法、滑模法、LQ[3]等。传统的PID控制器采用控制目标与实际输出之间的误差产生控制策略，但其调整时间较长，抗干扰能力较弱等缺点不能很好的满足四旋翼飞控系统动态指标的实现。而后面这些基于现代控制理论的方法一般需要精确的数学模型且算法复杂，不利于实际控制应用。

我国学者韩京清[4]提出的自抗扰控制方法是一种新型的控制技术，具有抗干扰能力强、响应速度快及算法简单的特点，在大量理论研究和工程实际中均得到应用。它通过状态观测器实时估计系统在工作时受到的外界干扰及系统本身的内扰，并对其进行补偿，从而得到优良的控制品质。本文设计了一种自抗扰控制器，并进行了仿真实验，检验了该自抗扰控制器的控制性能。

2四旋翼飞行器动力学模型

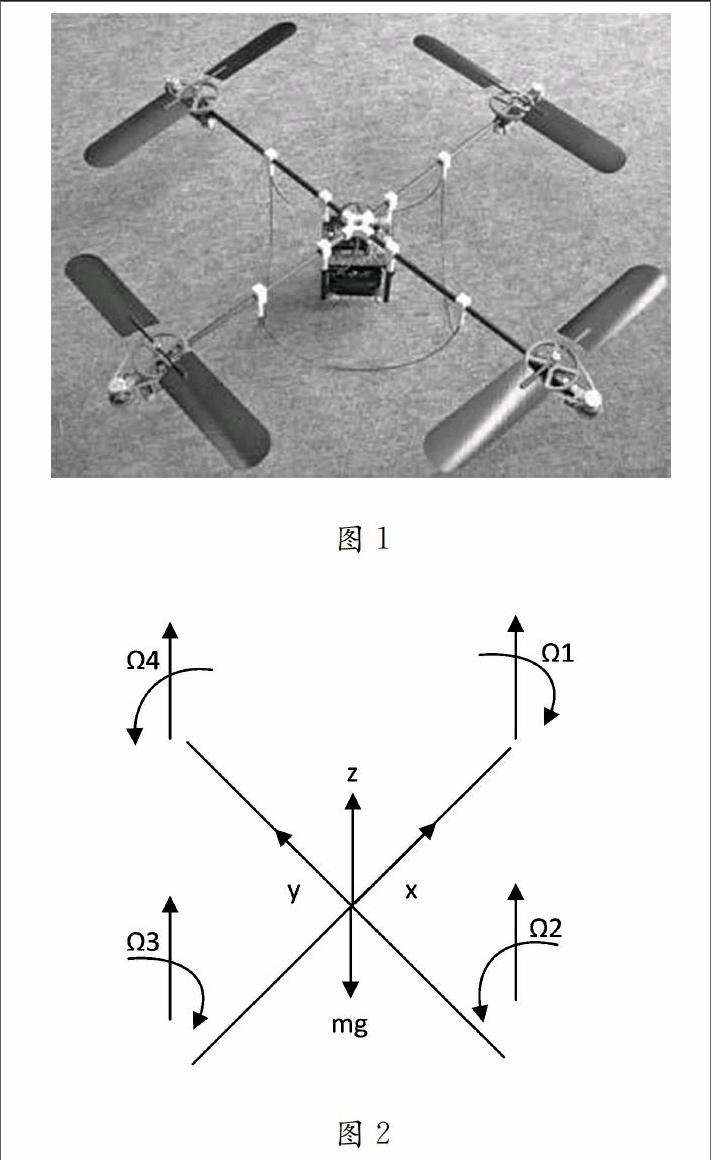
四旋翼飞行器如图1所示，具有四个对称分布的独立螺旋桨，由四个独立的电机驱动绕三个机体轴和沿三轴线进行六自由度[5][6]运动。根据牛顿-欧拉法，对四旋翼飞行器进行动力学建模。四旋翼飞行器坐标系如图2所示。

考虑到室内或室外无风条件下，四旋翼无人飞行器慢速飞行或悬停，对飞行器作以下假设：四旋翼飞行器为均匀对称的刚体，忽略旋翼中心至飞行器几何中心的垂直距离，忽略其它外界干扰。基于上述假设条件的四旋翼飞行器动力学模型为：

其中Φ、θ、ψ分别为俯仰角、滚转角、偏航角，IX、IY 、IZ分别为飞行器绕三个机体坐标轴的转动惯量，Jr为旋翼绕电机轴的转动惯量，Ωi为第i个旋翼的转速，U1=b（Ω12+Ω22+Ω32+Ω42）、U2=b（Ω42-Ω22）、U3=b（Ω32-Ω12）、U4=d（Ω12+Ω32-Ω22-Ω42），Ωr=Ω2+Ω4-Ω1-Ω3，b为推力系数，d为阻力系数。

3自抗扰控制器设计

3.1自抗扰控制器原理

自抗扰控制器的基本组成包含扩张状态观测器和扰动估计的补偿两部分，其中实时估计扰动及补偿的功能是自抗扰控制器最本质的功能。因此只要具有这个功能，该控制器即可称为自抗扰控制器[7]。如图3所示为一个典型的二阶自抗扰控制器。

3.2控制器设计方案

由式（1）可以看出四旋翼飞行器系统三个姿态通道存在耦合关系。但在姿态角速率变化较小时，相互间的耦合影响可以忽略，因此能够按单通道控制系统分别设计。本文所采用的PID-ADRC控制器由PID控制器和扩张状态观测器（ESO）组成，对俯仰、横滚、偏航、高度四个通道[8][9]独立控制，整个系统的结构如图4所示。

在姿态控制过程中，不希望角度响应存在超调，因为角度会影响位置的运动，角度偏大或者振动会导致多旋翼飞行器在飞行的过程中姿态不稳定，甚至有坠机的危险，所以不采用欠阻尼系统（0<ζ<1）。而在过阻尼（ζ>1）和临界（ζ=1）系统中，临界阻尼响应具有最短的上升时间和最快的响应速度[10]，所以取ζ=1。俯仰通道、偏航通道、高度通道同样取ζ=1。在临界阻尼系统中， ，当 时， ，不妨取 则 ， 。利用同样的方法可得相同的俯仰和偏航控制器参数。高度通道的参数整定和姿态器控制器相似，期望的调节时间为1～2秒，取ts=1s，则有 、 ， 。

由式（3）知道線性扩张状态观测器的特征方程[11]为s3+β01s2+β02s+β03，需选取合适的参数β01，β02，β03才能较为准确的估计被测对象的状态以及总扰动。通常较稳定的特征方程形式为（s+ω0）3，于是把参数β01，β02，β03配置成3ω0，3ω02，ω03形式。通常ω0=3～5ωc。

4仿真实验与结果分析

4.1姿态稳定控制实验

首先在SIMULINK中对四旋翼飞行器姿态稳定控制进行仿真实验。多旋翼飞行器的参数采用EPFL的OS4[12][13]飞行器（“十”字形四旋翼飞行器），其固有参数包括：质量m=0.65kg，机架臂长l=0.23m，Ix=0.0075kg·m2，Iy=0.0075kg·m2，Iz=0.013kg·m2。经过微调，控制器参数选取为：β01=120、β02=4800、β03=64000。设定初始横滚角为20?，俯仰角15?，偏航角10?，仿真指令是让飞行器从高度0m至2m将姿态角稳定在0?。仿真曲线如图9所示。

从图9可以看出， 三个姿态角在0.8s内，高度在1.5s左右达到设定值， 没有超调，振荡极小，体现了该控制器的姿态稳定控制能力。

4.2与PID控制器对比实验

在四旋翼飞行器的实际飞行过程中，会因为外界干扰出现轻微的抖动，该仿真实验模拟四旋翼飞行器在悬停时受外界干扰后姿态的调整过程。因四旋翼飞行器为对称结构，滚转角和俯仰角仿真曲线类似，限于篇幅，该实验只分析滚转通道与偏航通道。为了比较本文所设计控制器和PID控制器的抗扰动能力，在横滚通道加入正弦干扰信号0.05sin（t），在偏航通道加入正弦干扰信号0.1sin（2t）。初始的滚转角、偏航角分别为10?、6?。仿真指令是将姿态角恢复到0?。两个通道的仿真曲线如图10所示，仿真测试时间为20S，在干扰力矩作用下，PID-ADRC控制器跟踪效果依然理想，满足预期的设计要求。而PID控制器的响应曲线虽然能够跟踪设定值，但会产生振荡。由实验数据可知，本文所设计控制器很好地跟踪并补偿了所加扰动。

5 结束语

（1）针对四旋翼飞行器动力学模型，设计了一种PID-ADRC自抗扰控制器。

（2）在SIMULINK中搭建了系统仿真图，并通过进行姿态稳定控制、干扰力矩作用下与PID控制器对比等仿真实验来验证所设计控制器的抗扰性和鲁棒性，仿真结果证明该控制器能够稳定运行，具有较好的鲁棒性与控制精度。

（3）由于扩张状态观测器将未建模动态、耦合影响及外部干扰影响作为总和干扰进行估计并动态反馈补偿，使得自抗扰控制器的设计无需精确的四旋翼飞行器被控模型，克服了实际中难以建立精确被控模型并获取外界干扰的困难，具有工程应用价值。

参考文献：

[1] Li Y， Song S. A survey of control algorithms for Quadrotor Unmanned Helicopter[A]. 2012

IEEE Fifth International Conference on.Advanced Computational Intelligence （ICACI），

Nanjing，China， 2012： 365-369.

[2] Madani T ，Benallegue A .Backstepping control for a quadrotor helicopter[A].Proceedings of

the 2006 IEEE/RSJ International Conference on International Conferrence on Intelligent

Robots and Systems[C].Beijing，China，2006：3255-3260.

[3] Bouabdallah S ，Noth A，Siegwart R.PID vs LQ control techniques applied to an indoor micro

quadrotor[A].Proceedings of the 2004 IEEE/RSJ International Conference on International

Conferrence on Intelligent Robots and Systems[C].Sendal，Japan，2004：2451-2456.

[4] Gao Z.Active Disturbance Rejection Control：A Paradigm Shift in Feedback Control System

Design [C].Proceedings of the 2006 American Control Conference Minneapolis， Minnesota，

USA， June 14-16， 2006.

[5] 齐晓慧， 王洪军.四旋翼无人机的自抗扰控制研究[J].测控技术， 2014 ，33（5）： 61 – 64.

[6] 李毅，陈增强，刘忠信.自抗扰技术在四旋翼飞行姿态控制中的应用[J].哈尔滨工业大学

学报，2014，46，（3）.

[7] 韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术[M].北京：国防工业出版

社，2008.

[8] 张广昱，袁昌盛. 基于自抗扰理论的小型四旋翼飞行器姿态控制[J].航空工程进展，

2014 ，5 （3）.

[9] 刘一莎，杨晟萱，王伟.四旋翼飞行器的自抗扰飞行控制方法[J].控制理论与应用，2015

，32（10）.

[10] 胡寿松. 自动控制原理 （修订本）[M]. 北京： 机械工业出版社， 2008.

[11] Gao Z. Scaling and bandwidth-parameterization based controller tuning[C].Proceedings of

the American control conference. 2006， 6： 4989-4996.

[12] Bouabdallah S. Design and control of quadrotors with application to autonomous

flying[D]. ?cole Polytechnique federale de Lausanne， 2007.

[13] Lim H， Park J， Lee D， et al. Build your own quadrotor： Open-source projects on unmanned

aerial vehicles[J]. Robotics & Automation Magazine， IEEE. 2012， 19（3）： 33-45.