配送中心分区同步拣货系统品项均衡分区研究

文/马小霞 苏辉辉 梁艳 杨惠惠

配送中心分区同步拣货系统品项均衡分区研究

文/马小霞 苏辉辉 梁艳 杨惠惠

分区拣货作业是配送中心常见的一种人至货的拣选方式，由于多人同时对一个订单进行拣货作业，如果订购品项在拣选区的分布不均衡，导致了拣货人员的工作量有差异，而造成作业中的空闲等待时间，形成了浪费，且订单需求的品项种类不同，数量也有差异，这些都导致了均衡储存的复杂性，本文拟在货品进行入库前对储位进行优化，按照订单的历史数据将货品均匀地分布在各个拣选区，来平衡拣货人员的工作负荷。

分区拣货；储位优化；均衡储存

引言

随着物流业的不断发展，仓储管理在现代物流环节中占据越来越重要的地位，成为其必不可少的一环。拣选作业在仓储作业中消耗的人力成本、设备成本和时间成本非常高，成为影响仓储作业效率的瓶颈。在配送中心中，分拣作业时间约占全部作业时间的40%以上，拣选成本一般要占全部运营成本的65%以上，因此，合理优化订单拣选作业，对配送中心作业效率的提高具有重要影响[1]。

分区拣货是将拣货作业场地分成多个区域，由一个或一组拣货人员负责捡取自己负责区域的物品[2]。分区拣货是一种比较好的拣选策略，目前的研究成果主要分为分区接力拣选和分区同步拣选，分区拣货不能保证订单的完整性，但拣选效率较高。在并行分区拣选中，由于储位安排不合理，员工对货位的熟悉情况、拣货速度的差异等因素造成了工作负载不均衡，部分分区拣货员忙碌，部分拣货员空闲等情况，造成了劳动力资源的浪费，影响了拣货系统的整体效率。工作负载不均衡在人工拣货系统成为瓶颈也是亟待解决的问题。

1.分区同步拣货模式研究现状

Speaker最早提出配送中心分区拣选作业策略[3]。EleonoraB，MargheritaC，GiuseppeV为了简化拣选作业，减少拣选过程中的行走时间为目的，在分区存储系统分配中，采用遗传算法确定订单品项的分配，有效降低拣选距离和拣取成本[4]。Sebastian介绍了并行分区中的上线订单分批问题，在客户订单到达的一定时间内，以最大化完工时间为目标，进行储位优化，设计了启发式算法求解物料的拣选顺序[5]。

国内文献中关于分区同步拣货模式的研究有：李诗珍重新定义了分区同步拣货系统储位分配中的相似系数，提出了当量订购次数[6]。蒋淑华结合并行分区拣货的特点，将EIQ分析法和订单的相关品项进行结合来安排储位[7]。张贻弓和吴耀华在品项间相似系数中考虑了拣选数量的影响，将货物品项分配问题归结为聚类问题，结合最大最小蚁群算法进行求解[8]。雷斌、蒋兆远、马殷元提出了静态分区、动态分配拣货人员的方法，建立人员调度模型，动态调度各分区拣货人员的数量[9]。李晓春、钟雪灵、王雄志考虑拣货员速度不同情况下，通过对品项在各分区的储位安排来平衡分区作业时间[10]。许小利、崔雪丽以不同分区的拣选时间趋于均衡作为储位优化目标，建立储位优化数学模型，采用遗传算法求取最优解[11]。

综上所述，有关分区同步拣货模式的研究集中在拣选目标、优化方法上，从拣货员的角度出发研究较少。拣货员具有主观能动性，从拣货员工作量出发，平衡拣货数量差异是非常有必要的，它可以提高员工拣货积极性，同时避免工作负载不均衡造成的资源闲置，解决分区同步拣货系统出现的延迟误差等瓶颈问题。

2.品项均衡分区模型

2.1 思路与目标

品项均衡分区模型的关键是货物的关联性，即货物间的相似系数。例如顾客在订购产品A时，同时会订购其他品项B或C，这些货物经常同时拣取，这些货品之间存在着关联性。不同的货品在一个订单中出现的次数越多，说明关联性越强，相似性越高。在正常的储位优化中，一般都是以拣选时间最短，或拣选距离最短为目标将相似性大的品项临近存放，即如果品项A和B的相似性系数越大，越要放置在同一拣选区，而本章研究的品项均衡分区模型利用逆向思维，将这种关联性强或者相似系数大的产品放在不同的区域，用来平衡拣选人员的工作量。

2.2 前提假设

在拣选系统已知的条件下，为便于建立数学模型，作一下假设：

1）每个订单订购不同的品项，且品项的数量较少

2）每种品项的分布在一个货架上，没有同种货品有多个货架现象

3）品项的重量、体积较小，数量较少的同种类品项一次可同时拣取

4）每个拣货员的动作都符合标准，即拣取品项所花的时间相同

5）各分区拣选人员独立进行拣选

根据以上假设，各分区的拣选作业时间与工作负荷与各分区中货品的种类、数量有关。订单的完成时间是分区中拣选作业时间最长的。

2.3 模型建立

对于并行分区的人工拣选系统来说，货品的单次拣取时间就是货品被拿取的时间，所以拣选分区的拣选时间与货品订货量、单次拣选量和订货次数有关。

假设拣取商品的重量和体积较小，一次可以拣取多个同类的品项，相似系数可以表示为：

Nab=Nba=

na表示品项A可以一次可以拣取的数量；nb表示品项B可以一次拣取的数量。

符号说明：

m 拣货分区数量

n 订单数量

q 品项数量

Nab、Nba品项A和品项B被同时订购的次数

xij0-1变量，品项j是否在订单i中

yak0-1变量，品项A是否在分区k中

na、nb品项A和品项B一次可拣取的数量

依照这个思路建立以下模型：MinF=

约束条件：

=1 1≤a≤q

1≤a≤q，1≤k≤m 1≤b≤q，1≤k≤m

Nab≥0

当相似系数Nab很大时，要得到函数的最优解，yak和ybk必然不能同时取1，品项A和品项B不能在同一个区存储；约束条件2保证了一个品项只能存储在一个区中。

3.算法设计

依据历史订单求出各个品项的相似系数Nab，并进行升序排列，一般假设为：

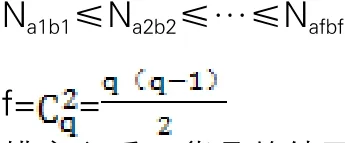
排序之后，货品的储区分配步骤如下：

Step1：将Na1b1最小的品类A1B1分配到第1个区Z1中，令j=1。

Step2：找出下一个最小的相似系数Nasbs，且品项As、Bs均未分配到分区中，将As、Bs分配到第j+1区中Zj+1，j=j+1。

Step3：当j＜m时，转Step2，否则转Step4，保证了分区中有两个初始的货品。

Step4：继续寻找下一个最小的相似系数Nalbl，且品项AlBl至少有一个未指派到分区中，Zj为已经分配到j区的品类集合，1≤j≤m。

Step5：

1）如果Bt已分配，At未分配，令表示Zj中每个品类e与品类At的相似度系数之和，将品项At分配给j*区。

2）如果品项At、Bt均未分配，则令Sj=，

如果Sj*≤Tj**，品项At分配到j*区，并且对j*区的相似度系数之和Tj=进行更新，Tj**=将Bt分配到j**区。

如果Sj*＞Tj**，品项Bt分配到j**区，并且对j**区的相似度系数之和Sj=进行更新，Sj*=将At分配到j*区。

Step6：当所有的品类都分配至各个分区中，停止，否则，继续Step4

在上述计算过程中，当出现相同的Sj*和Tj**时，将品项At和品项Bt优先分配到品种类较少的区中，当各区的品类数相同时，任意选一个区进行分配。

4.评价指标

优化模型的首要目标是各个拣选分区的工作人员拣选总量差最小。依据订单信息，拣货员的误工率越小方案越均衡，越大方案越不均衡。具体的步骤是：

1.计算各拣货员所用的总拣货时间

由假设可知，本文的拣货人员的工作负荷与货品的拣货数量和拣货时间有关系，订单拣选的总完成时间是分区中拣货时间最大的，因此首先计算各分区拣货员的总时间。计算公式为：

Tz=tz*Qz

其中：Tz—拣货员Z所用的总拣货时间

tz—拣货员Z拣选每一品项平均所需时间

Qz—分区Z中的品项数量集

2.计算各分区平均拣货时间

如果每个拣选分区的拣货时间都可以接近平均拣货时间，则说明各拣货分区之间的工作负荷均衡。分区平均拣货时间的计算方式是所有拣货人员的总拣货时间除以拣货分区数m。计算公式为：

3.计算拣货员Z的总拣货之间占分区平均拣货时间的比例

以平均拣货时间为基础，计算拣货员Z的总拣货时间占分区平均拣货时间的比例，比例系数越接近1，说明差距越小，表明各分区拣货工作量越均衡。计算公式为：

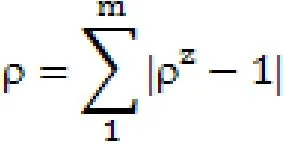
4.计算每个拣货员完成拣货任务的时间的差异率之和

综合上式，计算拣选分区的工作量的总差距，具体为将所有拣选分区的拣选时间差异率求和，计算公式为：

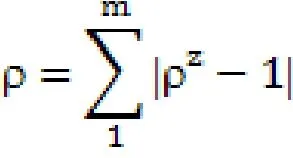
将拣货任务完成的时间的差异率之和定义为误工率，该系数越小方案越均衡，越大该方案越不均衡。

5.实验与结果

选取配送中心的8种货品，16个订单的数据，进行品项均衡分区模型的研究，在excel进行VB语言的求解

产品的相似度系数之和：

?

目前的分区结果如下：

分区1 分区2 分区3 HEA GFD CB

验证如下：

假设拣货员之间的速度恒定且相差不大，拣货能力相当，将拣取速度与行走速度合并视为拣货速度，假设为VZ，用1表示拣货员在单位时间可拣取的品项数量，则拣货员Z拣选每一品项所需的时间为：

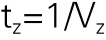
以下为一天中收到的订单数

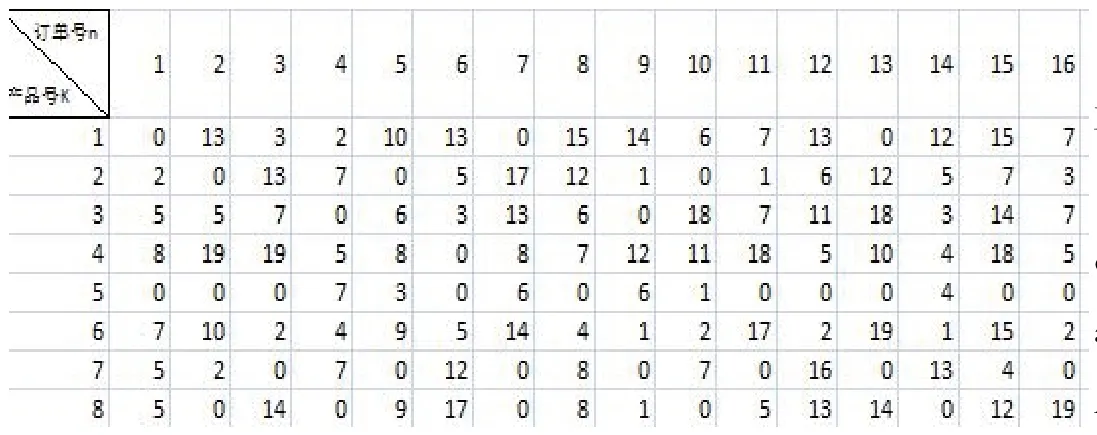
按照模型进行分区后的品项数量为：

分区一：130+27+117=274 分区二：114+74+157=345分区三：91+123=214

由假设可知，t1=t2=t3，则

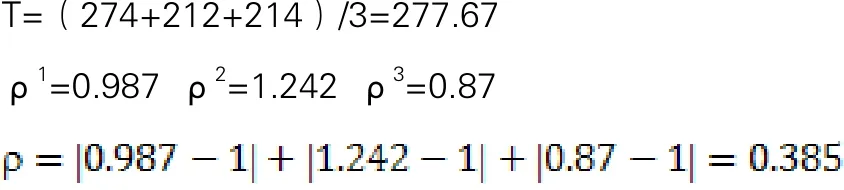
随机分类下分区：

分区一：130+91+123=344 分区二：74+114=188 分区三：157+27+117=301

由以上结果可知，分区后的误工率值明显小于随机存储下的值，该品项均衡分区模型具有适用性。

在分区同步拣货作业中，各分区的拣选作业同时进行，订单的完成时间取决于拣选作业之间最长的那个分区。因此，品项在分区中的均衡存储，对于平衡拣选人员的工作负荷和缩短订单完成时间非常重要。受约束理论的均衡思想启发，本文以配送中心同步拣选系统为研究对象，研究了如何均衡分区的问题，提出了基于工作量均衡的储位优化方法，分析历史订单，挖掘品项的相似性关系，建立工作量均衡的储位分区模型，设计启发式算法进行模型的求解，最后提出了误工率评价方法，证明此优化方法是有效的。

（作者单位：北京物资学院）

[1]De Koster R，Le～Due T，Roodbergen K J．Design and control of warehouse order picking：a literature review[J]．European Journal of Operational Research，2007，182（2）：481～501．

[2]吴颖颖．分区自动拣选系统拣选策略优化研究[D]．济南：山东大学，2012．

[3]Speaker，R．L．，Bulk order picking[J]．Industrial Engineering，1975，7（12），14～18．

[4]Eleonora B，Margherita C，Giuseppe V，et al．Optimisation of storage allocation in order picking operations through a genetic algorithm [J]．International Journal of Logistics：Research and Applications，2012，15（2）：127～146．

[5]Sebastian H．Algorithms for on～line order batching in an order picking warehouse [J]．Computers & Operations Research，2012，39：2549～2563．

[6]李诗珍．基于工作量均衡的分区同步拣货系统储位分配与评价[J]．包装工程，2010（11）：114～118．

[7]蒋淑华．EIQ法在并行分区储位优化中的应用[J]．物流技术，2010（7）：71～72．

[8]张贻弓，吴耀华．基于并行拣选策略的自动拣选系统品项分配[J]．计算机集成制造系统，2010（8）：1720～1725．

[9]雷斌，蒋兆远，马殷元．配送中心分区同步拣货系统人员分配策略研究[J]．计算机工程与应用，2014，50（24）：4～9．

[10]李晓春，钟雪灵，王雄志．并行分区拣货系统储位优化设计[J]．计算机工程与应用，2013，49（19）：20～24．

[11]许小利，崔雪丽．基于遗传算法的分区拣选系统储位优化实证研究[J]．包装工程，2015，36（19）：139～144．