2016年普通高等学校招生全国统一考试理科数学试题分析

辽宁省招生考试办公室 高考命题处

Ⅰ.试题评价

◇一、总体评价

2016年普通高等学校招生全国统一考试数学（文、理）试题是在进一步贯彻《国务院关于深化考试招生制度改革的实施意见》的背景下，参照2015年全国统一考试数学试卷命制的，符合新课程标准《考试大纲》和《考试说明》的要求。试卷的整体结构保持了2015年试卷的风格，而整体难度较2015年有所增加。试题设计体现了“朴实中重基础、常规中见能力、平和中透灵气”的稳健、成熟设计理念，体现了“一点四面”原则。从多视角、多维度、多层次考查数学思维品质，考查考生对数学本质的理解及数学素养和学习潜能。试卷注重文、理科考生在所学内容、能力和要求上的差异。试题布局合理，基本按照由易到难的顺序进行安排，有较好区分度，无偏、难、怪试题，有利于选拔人才，促进社会公平，推进课程改革，维护社会稳定。

◇二、主要特色

（一）执行课程标准，注重全面考查

1.指向性明确，回归本真

如第6题考查三视图，虽未指出主视图、左视图、俯视图，但不会产生任何歧义，就是圆柱与圆锥组合体的计算；第8题考查程序框图，是一道真正意义上的算法考查题目，考查学生的识图能力。

2.选择题简洁平稳，填空题难度适中，解答题层次分明。

3.注重对基础知识、基本技能、基本思想、基本体验的考查

试题既考查了传统的“三基”，又考查了基本体验过程，如第12题分析函数关于（0，1）对称，然后利用图像和性质加以分析和解决问题。

4.选材合理，回归教材

相当一部分试题来自于教材，如 1、2、3、4、8、9、10、13、14，特别是第10题用随机模拟方法近似计算原型，取材于必修三第三章几何概型例3中撒黄豆的模拟实验，是同一性质的两种体现形式。

5.抓住数学主干，考查通性通法

六道解答题突出考查了代数（函数与导数）、几何（立体和解析）、数列、概率与统计、三选一的知识，解决方法常规化。

6.尊重个体差异，体现课改精神

试卷的考查具有一定的灵活性。第10题设计较为抽象，但考生只要能联想教材中撒黄豆的模拟实验，就不难解决；第17题等差数列和取整函数的结合，不少考生难以辨别，对知识的迁移和应用知识解决问题的能力要求较高，给品质优秀、数学成绩良好的考生留有较大的展示空间，体现了课改精神。

7.体现“一点四面”原则

第8题程序框图与秦九韶算法思想相结合，把古代传统文化固化在数学试题中，考查学生对传统文化的理解和掌握情况，展现数学的科学价值和人文价值。

8.考点全面，呈现亮点，囊括重点、难点、热点、易错点

考点覆盖全面，同时重点突出，如第7题考查三角函数的图像变换和性质；第9题考查了三角变换和诱导公式；第13题考查了正弦定理和同角三角函数关系式；第17题虽是等差数列与取整的简单结合，但不少考生分辨不清，造成错解；第11题解析几何以图为主，辅以计算的热点问题温度不降；第21题借助导数证明不等式、求函数最值等难度不减；第20题解法上显得“任性”，也是答案的一个亮点，直接通过方程思想解出M、N的坐标比较简单，但很多考生由于平时练习中采用根与系数关系求解，导致忽略通过A的坐标与两根之积的关系得出M、N的坐标，使得此题略显繁琐。

（二）突出数学本质，侧重考查思想方法

如第21题，综合考查函数与方程、数形结合、对称、化归与转化等思想；第24题综合考查了分类与整合、函数与方程思想；第12、20题考查了数形结合思想；第19题考查了化归与转化思想。

（三）重视知识联系，强化能力立意

1.注重在知识交汇处设计试题

在概率和统计知识交汇处命题是高考常见的考查方式，第18题亦是如此；第21题是在函数、导数、不等式的交汇处设计的题目。

2.以知识为载体，数学思维能力为核心

整张试卷全面考查了数学的五个能力，考查理性思维的广度和深度。第6、14、19题考查空间想象力、运算求解、推理论证能力；第22题考查推理论证和运算求解能力；第18题考查数据和图表的分析与处理能力；第5、10、15题考查逻辑推理、应用和创新能力；第12题考查抽象概括、运算求解能力。

（四）贴近生活实际，体现应用意识和创新意识

结合考生生活实际设计试题，如第5题背景是最短路径问题，看似新颖，实则考查乘法原理；第18题是与现实生活密切联系的续保问题，看似设问较多，但难度不大，通过对数据的分析与处理，综合考查统计问题并求解互斥事件有一个发生及条件概率问题。

◇三、对2017年高考试题的建议

在保持平稳的基础上，适当增加亮点和创新点。

◇四、试卷的统计数据分析

数学（理科）

2016年辽宁参加考试的考生人数：134675人，总体平均分：83.9966分，最高分：149分，最低分：0分，难度系数：0.56，标准差：28.7598，区分度：0.4703，α 信度：0.8726。

Ⅰ.试题分析

第Ⅰ卷

一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知 z=（m+3）+（m-1）i在复平面内对应的点在第四象限，则实数m的取值范围是

（A）（-3，1） （B）（-1，3）

（C）（1，+∞） （D）（-∞，-3）

【答案】A

【解析】本题主要考查复数的几何意义.

点（m+3，m-1）在第四象限，解得-3＜m＜1.

【数据分析】

题号 人数 满分人数 零分人数1 134675 122313 12362平均分 方差 标准差 难度4.541 2.0841 1.4436 0.9082

（2）已知集合A=｛1，2，3｝，

【答案】C

【解析】本题主要考查集合的运算、不等式的解法.集合B由哪些整数构成是易错点.

【数据分析】

题号 人数 满分人数 零分人数2 134675 104559 30116平均分 方差 标准差 难度3.8819 4.3403 2.0833 0.7764

（3）已知向量 a=（1，m），b=（3，-2），且（a+b）⊥b，则m=

（A）-8 （B）-6 （C）6 （D）8

【答案】D

【解析】本题主要考查向量垂直的充要条件、向量的坐标运算.由（a+b）·b=0 解得 m=8.

【数据分析】

题号 人数 满分人数 零分人数3 134675 124554 10121平均分 方差 标准差 难度4.6242 1.7376 1.3182 0.9248

（4）圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1，则a=

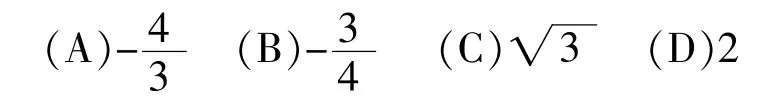
【答案】A

【解析】本题主要考查圆的一般方程式，圆心的坐标公式及点到直线的距离公式.由圆心（1，4）到直线ax+y-1=0的距离

【数据分析】

题号 人数 满分人数 零分人数4 134675 114899 19776平均分 方差 标准差 难度4.2658 3.132 1.7697 0.8532

（5）如图，小明从街道的E处出发，先到F处与小红会合，再一起到位于G处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为

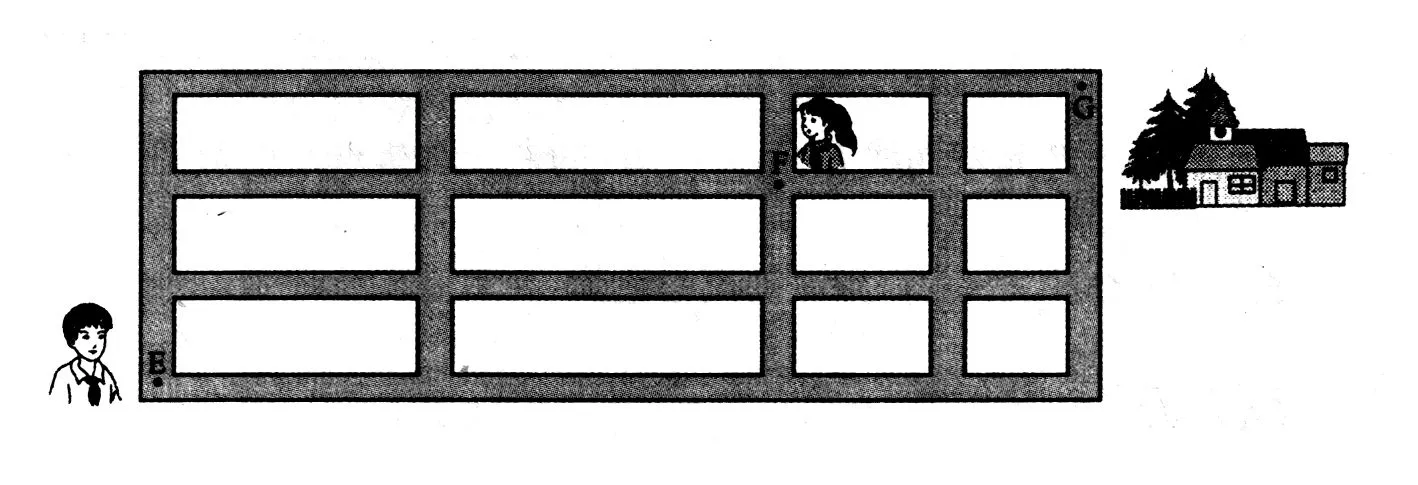
（A）24 （B）18 （C）12 （D）9

【答案】B

【解析】本题主要考查计数原理及用排列、组合知识解决实际问题的能力.从E到F分四步，其中两步向上，从F到G分三步，其中一步向上，故18.

【数据分析】

题号 人数 满分人数 零分人数5 134675 93026 41649平均分 方差 标准差 难度3.4537 5.3404 2.3109 0.6907

（6）下图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为

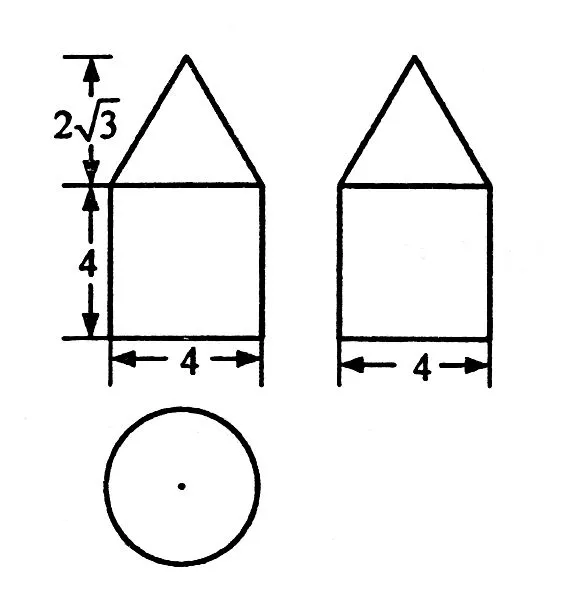
（A）20π （B）24π （C）28π （D）32π

【答案】C

【解析】本题主要考查三视图、几何体的表面积.该几何体是圆柱和圆锥的组合体，其中圆柱的底面半径为2，高为4，圆锥的底面半径为2，母线长为4.

【数据分析】

题号 人数 满分人数 零分人数6 134675 93900 40775平均分 方差 标准差 难度3.4862 5.2775 2.2973 0.6972

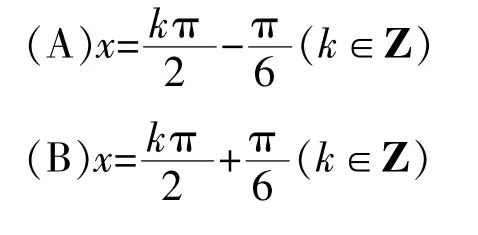
【答案】B

【解析】本题主要考查三角函数的图像与性质.将函数y=2sin2x的图像向左平移个长度单位后，得到可得平移后函数图像的对称轴方程.

【数据分析】

题号 人数 满分人数 零分人数7 134675 110358 24317平均分 方差 标准差 难度4.0972 3.699 1.9233 0.8194

（8）中国古代有计算多项式值的秦九韶算法，下图是实现该算法的程序框图.执行该程序框图，若输入的 x=2，n=2，依次输入的 a 为 2，2，5，则输出的s=

（A）7 （B）12 （C）17 （D）34

【答案】C

【解析】本题主要考查对程序框图的理解.该程序框图运行3次，各次s的取值依次为2，6，17.

【数据分析】

题号 人数 满分人数 零分人数8 134675 129585 5090平均分 方差 标准差 难度4.811 0.9092 0.9535 0.9622

【答案】D

【解析】本题主要考查三角恒等变换，包括诱导公式、二倍角公式等.并且题目很灵活，其解法并不唯一，如

【数据分析】

题号 人数 满分人数 零分人数9 134675 103456 31219平均分 方差 标准差 难度3.841 4.4519 2.11 0.7682

（10）从区间[0，1]随机抽取 2n 个数 x1，x2，…，xn，y1，y2，…，yn，构成 n 个数对（x1，y1），（x2，y2），…，（xn，yn），其中两数的平方和小于1的数对共有m个，则用随机模拟的方法得到的圆周率π的近似值为

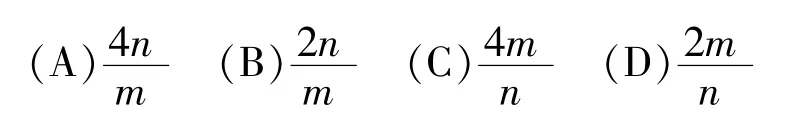
【答案】C

【数据分析】

题号 人数 满分人数 零分人数10 134675 62796 71879平均分 方差 标准差 难度2.3314 6.2216 2.4943 0.4663

（11）已知 F1，F2是双曲线的左，右焦点，点M在E上，MF1与x轴垂直，sin∠MF2F1=则E的离心率为

【答案】A

【数据分析】

题号 人数 满分人数 零分人数11 134675 101742 32933平均分 方差 标准差 难度3.7773 4.6185 2.1491 0.7555

（A）0 （B）m （C）2m （D）4m

【答案】B

【解析】本题主要考查函数图像的中心对称性及数形结合思想.由题意两个函数的图像都关于点（0，1）中心对称，则图像交点两两关于点（0，1）对称，所以

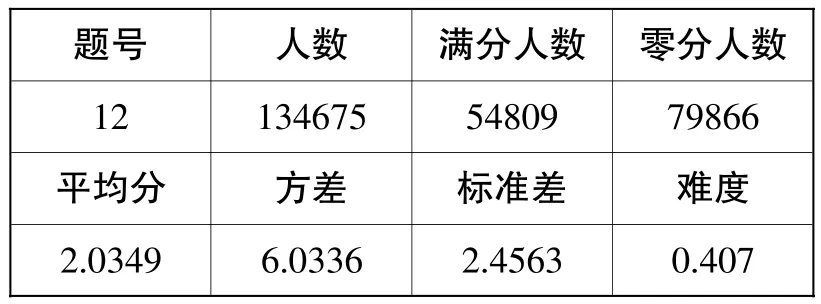
题号 人数 满分人数 零分人数12 134675 54809 79866平均分 方差 标准差 难度2.0349 6.0336 2.4563 0.407

第Ⅱ卷

本卷包括必考题和选考题两部分。第13～21题为必考题，每个试题考生都必须作答。第22～24题为选考题，考生根据要求作答。

二、填空题：本题共4小题，每小题5分。

（13）△ABC 的内角 A，B，C 的对边分别为 a，b，

【数据分析】

题号 人数 满分人数 零分人数13 134675 64930 69745平均分 方差 标准差 难度2.4106 6.242 2.4984 0.4821

（14）α，β 是两个平面，m，n 是两条直线，有下列四个命题：

①如果 m⊥n，m⊥α，n∥β，那么 α⊥β.

②如果 m⊥α，n∥α，那么m⊥n.

③如果 α∥β，m⊂α，那么 m∥β.

④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等.

其中正确的命题有_____.（填写所有正确命题的编号）

【答案】②③④

【解析】本题主要考查空间直线与平面的位置关系.熟悉线面位置关系的性质与判定定理是解题关键.

【数据分析】

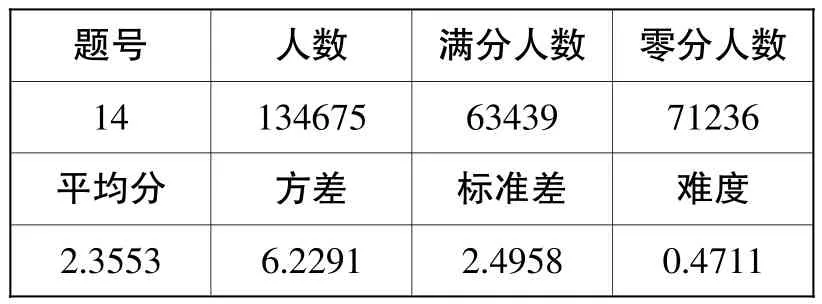
题号 人数 满分人数 零分人数14 134675 63439 71236平均分 方差 标准差 难度2.3553 6.2291 2.4958 0.4711

（15）有三张卡片，分别写有 1 和 2，1 和 3，2 和3.甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是_____.

【答案】1 和 3

【解析】本题主要考查解决实际问题时的逻辑推理能力.按照甲、乙、丙三个人的说法将所有可能的情况列出，再排除相互矛盾的.

【数据分析】

题号 人数 满分人数 零分人数15 134675 122713 11962平均分 方差 标准差 难度4.5559 2.0233 1.4224 0.9112

（16）若直线y=kx+b是曲线y=ln x+2的切线，也是曲线y=ln（x+1）的切线，则b=_____.

【答案】1-ln2

【解析】本题主要考查导数的几何意义，对运算能力要求较高.由解得，2-ln2）在直线 y=kx+b 上得b=1-ln2.

【数据分析】

题号 人数 满分人数 零分人数16 134675 13803 120872平均分 方差 标准差 难度0.5125 2.2997 1.5165 0.1025

三、解答题：解答应写出文字说明、证明过程或演算步骤。

（17）（本小题满分 12 分）

Sn为等差数列｛an｝的前n项和，且a1=1，S7=28.记bn=[lg an]，其中[x]表示不超过x的最大整数，如[0.9]=0，[lg 99]=1.

（Ⅰ）求 b1，b11，b101；

（Ⅱ）求数列｛bn｝的前1000项和.

【答案】

解：（Ⅰ）设｛an｝的公差为d，据已知有7+21d=28，解得 d=1.

所以｛an｝的通项公式为an=n.

所以数列｛bn｝的前1000项和为1×90+2×900+3×1=1893. ……12分

【解析】本题主要考查等差数列、数列求和及对取整函数的理解，考查分类讨论的数学思想.

【数据分析】

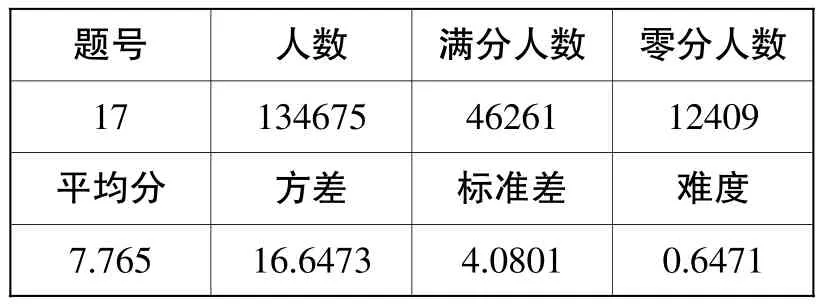
题号 人数 满分人数 零分人数17 134675 46261 12409平均分 方差 标准差 难度7.765 16.6473 4.0801 0.6471

（18）（本小题满分 12 分）

某险种的基本保费为a（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：

上年度出险次数 0 1 2 3 4 ≥5保费 0.85a a 1.25a 1.5a 1.75a 2a

设该险种一续保人一年内出险次数与相应概率如下：

一年内出险次数 0 1 2 3 4 ≥5概率0.30 0.15 0.20 0.20 0.10 0.05

（Ⅰ）求一续保人本年度的保费高于基本保费的概率；

（Ⅱ）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率；

（Ⅲ）求续保人本年度的平均保费与基本保费的比值.

【答案】

解：（Ⅰ）设A表示事件：“一续保人本年度的保费高于基本保费”，则事件A发生当且仅当一年内出险次数大于1，故

P（A）=0.2+0.2+0.1+0.05=0.55. ……3分

（Ⅱ）设B表示事件：“一续保人本年度的保费比基本保费高出60%”，则事件B发生当且仅当一年内出险次数大于3，故

P（B）=0.1+0.05=0.15

又 P（AB）=P（B），故

（Ⅲ）记续保人本年度的保费为X，则X的分布列为

X 0.85a a 1.25a 1.5a 1.75a 2a P 0.30 0.15 0.20 0.20 0.10 0.05

EX=0.85a×0.30+a×0.15+1.25a×0.20+1.5a×0.20+1.75a×0.10+2a×0.05=1.23a.

因此续保人本年度平均保费与基本保费的比值为1.23. ……12分

【解析】本题主要考查互斥事件的概率、条件概率及离散型随机变量的概率分布和对实际问题建立数学模型的能力.

【数据分析】

题号 人数 满分人数 零分人数18 134675 32513 26611平均分 方差 标准差 难度6.8507 19.8066 4.4505 0.5709

（19）（本小题满分 12 分）

如图，菱形ABCD的对角线AC与BD交于点O，AB=5，AC=6，点 E，F分别在 AD，CD 上，AE=CF=，EF交BD于点H.将△DEF沿EF折到△D′EF的位置，

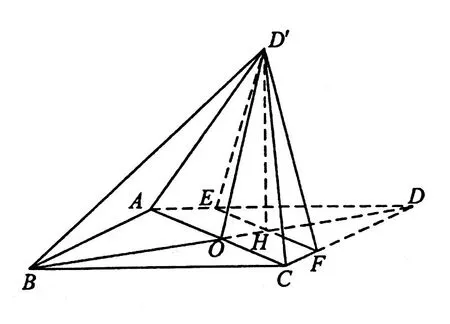
（Ⅰ）证明：D′H⊥平面 ABCD；

（Ⅱ）求二面角B-D′A-C的正弦值.

【答案】

解：（Ⅰ）由已知得 AC⊥BD，AD=CD.

因此 EF⊥HD，从而 EF⊥D′H.

所以 OH=1，D′H=DH=3.

于是 D′H2+OH2=32+12=10=D′O2，故 D′H⊥OH.

又 D′H⊥EF，而 OH∩EF=H，所以 D′H⊥平面ABCD. ……6分

（Ⅱ）如图，以H为坐标原点，HF的方向为x轴正方向，建立空间直角坐标系 H-xyz.则 H（0，0，0），A（-3，-1，0），B（0，-5，0），C（3，-1，0），D′（0，0，3），

设 m=（x1，y1，z1）是平面 ABD′的法向量，则

所以可取 m=（4，3，-5）.

设 n=（x2，y2，z2）是平面 ACD′的法向量，则

所以可取 n=（0，-3，1）. ……10 分

【解析】本题主要考查空间线面位置关系及空间向量的应用，考查空间想象能力、逻辑推理能力和运算能力.

【数据分析】

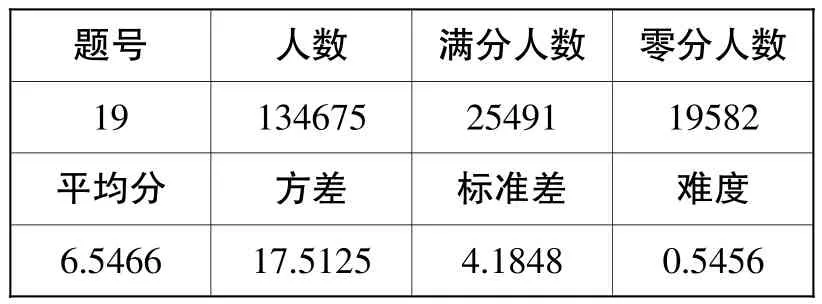
题号 人数 满分人数 零分人数19 134675 25491 19582平均分 方差 标准差 难度6.5466 17.5125 4.1848 0.5456

（20）（本小题满分 12 分）

解：（Ⅰ）设 M（x1，y1），则由题意知 y1＞0.

因此直线AM的方程为y=x+2.

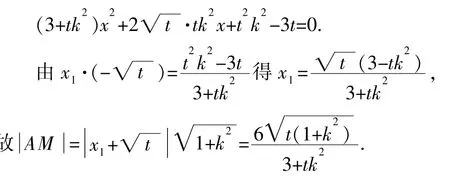
【解析】本题主要考查椭圆的标准方程、几何性质及直线与椭圆的位置关系，考查函数与方程的数学思想和运算能力.

【数据分析】

题号 人数 满分人数 零分人数20 134675 469 89895平均分 方差 标准差 难度1.4122 5.4586 2.3364 0.1177

（21）（本小题满分 12 分）

【答案】

解：（Ⅰ）f（x）的定义域为（-∞，-2）∪（-2，+∞）.

且仅当 x=0 时，f′（x）=0，所以 f（x）在（-∞，-2），（-2，+∞）单调递增.

因此当 x∈（0，+∞）时， f（x）＞f（0）=-1.

所以（x-2）ex＞-（x+2），（x-2）ex+x+2＞0. ……5 分

由（Ⅰ）知， f（x）+a 单调递增.对任意 a∈[0，1），f（0）+a=a-1＜0，f（2）+a=a≥0.

因此，存在唯一xa∈0，2]（，使得f（xa）+a=0，即g′（xa）=0.

当 0＜x＜xa时，f（x）+a＜0，g′（x）＜0，g（x）单调递减；

当 x＞xa时，f（x）+a＞0，g′（x）＞0，g（x）单调递增.

因此g（x）在x=xa处取得最小值，最小值为

综上，当 a∈[0，1）时，g（x）有最小值 h（a），h（a）的值域是

【解析】本题主要考查分析、解决问题及逻辑推理能力，是导数、函数知识的综合应用.

【数据分析】

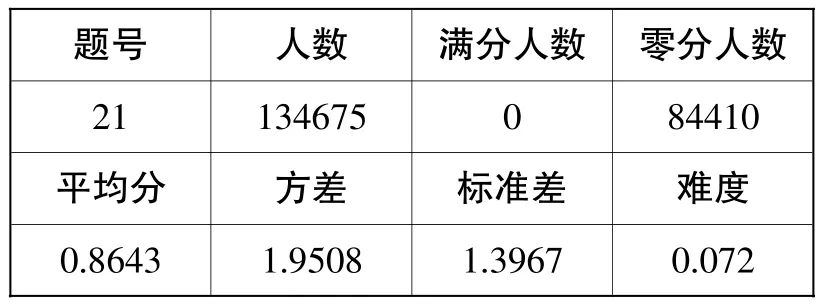
题号 人数 满分人数 零分人数21 134675 0 84410平均分 方差 标准差 难度0.8643 1.9508 1.3967 0.072

请考生在第22～24题中任选一题作答，如果多做，则按所做的第一题计分。做答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑。

（22）（本小题满分10分）选修4-1：几何证明选讲

如图，在正方形ABCD中，E，G分别在边DA，DC上（不与端点重合），且DE=DG，过D点作DF⊥CE，垂足为F.

（Ⅰ）证明：B，C，G，F四点共圆；

（Ⅱ）若AB=1，E为DA的中点，求四边形BCGF的面积.

【答案】

解：（Ⅰ）因为 DF⊥EC，所以△DEF∽△CDF，则有∠GDF=∠DEF=∠FCB，

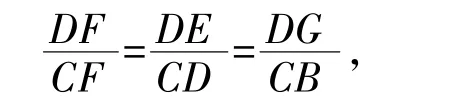
所以△DGF∽△CBF，由此可得∠DGF=∠CBF.

因此∠CGF+∠CBF=180°，所以 B，C，G，F 四点共圆. ……5分

（Ⅱ）由 B，C，G，F四点共圆，CG⊥CB 知 FG⊥FB.连结GB.

由G为Rt△DFC斜边CD的中点，知GF=GC，故Rt△BCG≌Rt△BFG，因此，四边形BCGF的面积S是△GCB的面积S△GCB的2倍，即

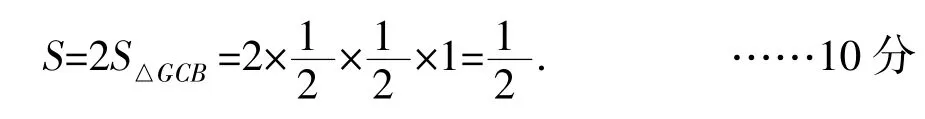
【解析】本题主要考查三角形相似、全等的判定与性质，考查逻辑推理和运算能力.

（23）（本小题满分10分）选修4-4：坐标系与参数方程

在直角坐标系xOy中，圆C的方程为（x+6）2+y2=25.

（Ⅰ）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；

【答案】

解：（Ⅰ）由 x=ρcosθ，y=ρsinθ可得圆 C 的极坐标方程

（Ⅱ）在（Ⅰ）中建立的极坐标系中，直线l的极坐标方程为 θ=α（ρ∈R）.

设A，B所对应的极径分别为ρ1，ρ2.将l的极坐标方程代入C的极坐标方程得

【解析】本题主要考查圆的极坐标方程、直线的参数方程，考查数形结合的数学思想.

（24）（本小题满分10分）选修4-5：不等式选讲

（Ⅰ）求 M；

【答案】

（Ⅱ）由（Ⅰ）知，当 a，b∈M 时，-1＜a＜1，-1＜b＜1，从而

【解析】本题主要考查（绝对值）不等式的解法与证明，考查逻辑推理及运算能力.

【数据分析】

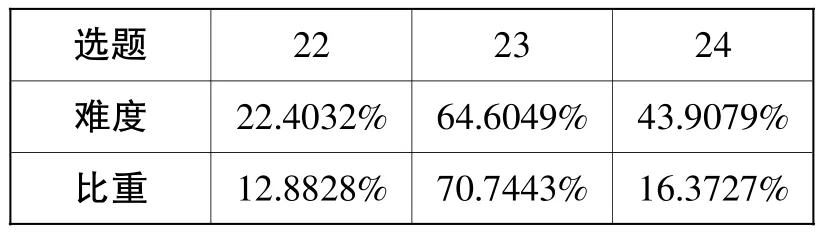
选题 22 23 24难度 22.4032% 64.6049% 43.9079%比重 12.8828% 70.7443% 16.3727%

Ⅲ.对2017年高考数学教学及备考建议

2016年高考全国统一考试数学试卷，尽管总体稳定，但还是向广大一线教师传递了几个讯息：高考试题在降低起点的同时，强调能力立意；在立足基础的同时，着力内容创新；在继承传统的同时，彰显新课程理念。预计这些特点在今后高考命题中会得到有效的保持和延续，基于此对今后的数学教学及复习备考提出以下几点建议：

◎一、了解课程标准，熟读《考试大纲》，紧扣《考试说明》，为高三复习指明方向

《新课程标准》是教学的指挥棒，《考试大纲》是高考命题的重要依据，《考试说明》为《考试大纲》的重要解读，在高一、高二教学中要认真落实，为高三复习保驾护航。

◎二、充分利用教材，挖掘数学本质，抓住数学主干，揭示数学知识的内在联系

题在书外，但理都在书中。2016年高考数学试卷中，许多题目都能在课本上找到“影子”，不少试题就是将课本题目进行引申、拓宽和变化。此外对支撑数学学科知识体系的重点内容保持了较大的比例。因此在教学中，应努力揭示数学概念、法则、结论的发展过程和本质，使学生体会蕴含在其中的思想方法，做到真正地用教材教而不是简单的教教材。回归教材并不等同于把教材重新回顾一遍，而是要将教材试题与高考试题相联系，找到两者的结合点。

◎三、认真钻研近几年全国统一考试高考试题，分析试题源头

高考试题往往来自以下几个方面：1.试题翻新于经典题目；2.试题取材于教材；3.试题源于竞赛或自主招生题目；4.试题借鉴于往年高考试题；5.试题下放于高等数学中的重要背景。

◎四、注重思想方法，提高学生的数学思维能力

高考是选拔性考试，2016年高考数学全国卷有一些创新题型，这些试题是以知识为载体，考查学生应用数学思想，独立解决问题的能力。因此在教学中应把数学思想贯穿于教学的始终，提高学生的数学思维能力和水平，进一步形成理性思考问题的习惯，学会用数学的思考方式解决问题、认识世界。

◎五、立足基础，重视通性通法，加强学生基本技能的训练

2016年高考数学全国卷命题把重点放在高中数学课程中最基础、最核心的内容上，关注学生在学习数学、解决数学问题过程中最为重要的、必须掌握的核心观念、基本常用技能，淡化技巧，对推理论证能力和抽象概括能力的考查贯穿于全卷，是考查的重点，兼顾考查空间想象能力和运算求解能力。因此在高中教学中，教师要重视学生运算、作图、推理、处理数据等基本技能的训练，删减人为技巧化难题，避免过于繁杂和技巧性过强的训练。高考不是比谁做得快，而是比谁做得好。在日常教学中，应注重学生使用通性通法解题能力的培养。

◎六、突出新课程理念，关注数学应用，发展学生的数学应用意识

新课标倡导积极主动、勇于探索的学习方式，倡导“学以致用”。2016年高考数学全国卷中对应用意识的考查坚持“贴近生活、背景公平、控制难度”的原则，这也体现了数学作为工具学科的应用价值。因此，在教学中教师要让学生体验数学发现和建模的过程，促进学生逐步形成和发展数学应用、创新意识，提高学生实践能力。

◎七、落实以生为本，改善教学方式和学习方式

1.学生能自己解决的事，教师决不要去包办代替

书要学生去念，题要学生去做，考试要学生去考，谁也无法代替。在高三数学复习中教师要切实发挥学生的主体作用，决不要去包办代替。高三数学复习的时间是很紧的，但再紧也不能紧学生参与教学活动的时间，要正确处理好讲与练的关系，切实做到宁可少讲两个题目，也要将参与教学活动的时间留给学生。最终通过教师的讲达到学生的“懂”，再通过学生的练达到学生的“会”，只有通过学生自己的实践、总结、思索、磨练才能达到“悟”的境界。

2.复习课讲落实

我们在高考复习中常听到有些教师非常气愤地说：“与某试题相类似的题目我已讲过多遍，你们怎么还是不会?”其中除了学生的原因外，与我们的复习方法有很大的关系，应该思考。从某种程度上来说，高三数学复习成败的关键在落实，教师在学生身上落实了多少，学生就考出多少。因此，要吃透学生，控制复习深度，要实事求是，把基础的东西夯实，然后有针对性的拔高，因材施教，方见成效。

3.培养兴趣，提升素养

对于学生来说，学数学不光是为了高考，更重要的是要培养对数学的兴趣，提升自身的数学素养。教师的教学尤其是高一、高二教学要重视知识生成的过程，重视学生在教学中的作用。学生如果对数学真的感兴趣，学好数学也就不成问题。

4.重视错误，让学生在纠错中成长

调查考入清华、北大的学生的学习方法，发现无一例外都具备一个错题本，可见纠错在学习中的重要性。教师教学中要善于抓住学生的错误，对症下药，让学生在纠错中成长。

5.注重细节，狠抓规范

不少考生甚至是水平较高的考生都会出现不能准确地表达所想的数学意思，或者是对一些严格要求格式的问题随心所欲作答，这都是平时疏于严格训练的结果。学生在学习中必须知道，学好数学不能仅满足于懂，还要善于准确、规范地表达。俗话说：“不怕难题不得分，就怕每题都扣分”。

执笔人：东北育才学校 刘新风

沈阳市第一二○中学 赵立强

葫芦岛市第一高级中学 王尚学