对“形形色色纸带问题”数据处理的探究
2017-07-11辽宁省实验中学北校白凤库
辽宁省实验中学北校 白凤库

高中物理有多个重要实验都涉及应用纸带。因此,纸带的数据处理(纸带类问题)就显得格外重要。为此,我把对纸带问题多年的教学和研究心得与广大同学们一起分享。
一、纸带问题数据处理的应用目的
应用纸带是多个高中物理实验中不可缺少的手段,应用纸带的目的是处理在力学实验中所要测得的有关数据。具体情况如下表所示:

实验名称 应用纸带的目的研究匀变速直线运动 求速度;求加速度探究加速度与力、质量的关系 求加速度验证机械能守恒定律 求速度探究功与速度变化的关系 求速度
从上表可以分析出,应用纸带的目的其实只有两个:一是求加速度;二是求速度。所以,纸带问题的核心就是学会应用测得的数据计算加速度和速度。
二、纸带问题数据处理的原理研究
1.关于速度的计算
纸带问题的速度计算无非是求平均速度或求瞬时速度。
(2)求瞬时速度思想:例如,测定第n点的瞬时速度的方法是,测出第n点的相邻前、后两段相等时间T内通过的距离Sn和Sn+1,如图所示:

【思考】求瞬时速度的实质也是求平均速度,即求以所求这一时刻为中间时刻的一段时间内的平均速度,而平均速度又等于位移与时间的比值,即:
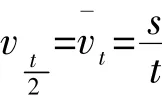
2.关于加速度的计算


【思考一】理解“任意性逐差”思想。

可以进一步得到 Sm-Sn=(m-n)aT2(其中,m>n),这样该思想就具有了“任意性”。
【思考二】认清逐差法本质精髓。以六段纸带为例求加速度,由逐差法可知:

六段纸带用逐差法的实质是将纸带分为两大段:设 T0=3T,y1=S1+S2+S3,y2=S4+S5+S6

如果是偶数段(4段、6段、8段等),按上述思想方法计算非常方便;如果是奇数段(5段、7段等),一般舍弃中间段然后用逐差法,也可舍弃第一段然后按上述偶数段方法计算(这两种舍弃方法各有利弊,这里不再赘述)。
【思考三】小心逐差法陷阱。

这样算出的最后结果只有S6和S1两组数据决定结果,另外四段数据没有起作用,这样误差将会较大。因此,在实验中,为了使实验结果更加精确,我们一般不采用这种计算方法。
三、纸带问题数据处理的几类典例
从一定意义上来说,纸带问题形形色色五花八门,揭开纸带问题神秘面纱,其实无非是以下四类纸带问题。
1.“理想纸带”类
所谓理想纸带类是指:在相邻相等时间内的位移差完全一样,没有任何差别。这样的纸带在现实实验中是不可能存在的,故称之为理想纸带。
例1在“探究小车速度随时间变化的关系”的实验中,所用交流电的频率为50Hz。某次实验中得到的一条纸带如图所示,从比较清晰的点起,每五个打印点取一个点作为计数点,分别标明0、1、2、3、4。 量得 S1=30.0mm,S2=36.0mm,S3=42.0mm,S4=48.0mm,则小车的加速度为____m/s2。(实验结果保留两位有效数字)

【解析】S2-S1=6.0mm,S3-S2=6.0mm,
S4-S3=6.0mm这就叫理想纸带类。故直接用ΔS=aT2求出加速度a=0.60m/s2
【说明】此类问题简单,只是直接应用原理。
2.“实际纸带”类
所谓实际纸带类是指:在相邻相等时间内的位移差不一样,但在误差允许范围内相等。这样的纸带在现实实验中是正常的,故称之为实际纸带。
例2某同学用打点计时器测定加速度,在得到的纸带上选取七个计数点(相邻两个计数点之间还有四个点未画出),如图所示,图中S1=4.81cm,S2=5.29cm,S3=5.76cm,S4=6.25cm,S5=6.71cm,S6=7.21cm。已知打点计时器所用交流电频率为50Hz,则加速度的大小为____m/s2(结果保留两位有效数字)。

【解析】从已知中可以明显看出相邻相等时间内的位移差不一样,这属于实际纸带,应用逐差法。根据前面所述逐差法的实质是将纸带分为两大段,然后用ΔS=aT2计算,这样更加方便。从一定意义上来说实现了“实际纸带向理想纸带”的飞跃。

【说明】将纸带看成两段的思想,计算起来更简捷一些。从一定意义上来说,例2和例1实现了完美的统一,即ΔS=aT2。
3.“跳跃纸带”类
所谓跳跃纸带类是指:题目中所给的数据不连续,往往根据不连续的两段测量数据进行计算,故称之为跳跃纸带。
例3 如图所示为某同学在 “测定小车运动的加速度”实验中,一次实验取得的纸带记录,已知电源的频率为50Hz,图中所标的是每5个点取一个点作为计数点,若A、B、E、F分别为第一、第二、第五、第六个计数点 (第三、四个计数点C、D图中未画出),则小车运动的加速度大小为a=____m/s2。

【解析】如果设AB间的距离为X1,则BC间距离为X2,CD间距离为X3,DE间距离为X4,EF间距离为 X5,根据 Sm-Sn=(m-n)aT2可知,X5-X1=4aT2,由此可计算出a=0.84m/s2。
【说明】对 Sm-Sn=(m-n)aT2理解到位,是解决此类问题的关键。
4.“抽象纸带”类
所谓抽象纸带类是指:从题目给的信息初步来看,不是纸带类问题。但是,经过仔细分析后发现其本质就是纸带类问题。故称之为抽象纸带类。
例4 为了测定某辆轿车在平直路上启动时的加速度(轿车启动时的运动可近似看作匀加速直线运动),某人拍摄了一张在同一底片上多次曝光的照片(如图甲)。如果拍摄时每隔2秒曝光一次,轿车车身总长为4.5米,那么这辆轿车的加速度约为____。

【解析】根据已知条件,我们可以把图甲变成图乙。于是,本题转化成纸带问题。根据ΔS=aT2可求出加速度约为2m/s2。
例5 如图甲所示,一个小球做平抛运动,用一张印有小方格的纸记录轨迹,小方格的边长为L=1.25cm。若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛运动的初速度大小是____,小球在b点的速率是____。 (取g=10m/s2,结果保留一位有效数字)

【解析】因为平抛运动的水平分运动是匀速运动,根据已知条件,我们根据图甲中的小球在水平方向上的分运动通过“投影”而形成的“水平纸带”(图丙)分析,a、b、c、d 之间是等时间隔的,设时间间隔为T,则有

同理,我们再根据“竖直纸带”(图乙)分析,显然可以直观地看出相邻相等时间内的位移差为

联立①②式得小球平抛的初速度大小是

b点速度的竖直分速度由“竖直纸带”(图乙)可得

小球在b点的速率是

联立②③④式得Vb=0.9m/s
例6 已知O、A、B、C为同一直线上的四点,AB间的距离为l1,BC间的距离为l2,一物体自O点由静止出发,沿此直线做匀加速运动,依次经过A、B、C三点,已知物体通过AB段与BC段所用的时间相等。求O与A的距离。
【解析】这道题根本没有纸带问题的“形”在,但却有纸带问题的“神”在,即题目中说“AB段与BC段所用的时间相等”。只要匀变速直线运动牵涉到等时间隔,往往可以联想纸带问题。设O与A的距离为l,物体的加速度为a,到达B的速度为vB,通过AB段和BC段所用的时间为t,则有

联立①②③式得:

【说明】从抽象纸带的三道例题可以看出,揭开题目表象的神秘面纱,然后用纸带问题的处理方法去解决,可以化难为易。解决纸带问题的方法,往往成为解决“牵涉等时间间隔的匀变速直线运动问题”的好方法。
