多部件串联系统的定期预防性维修策略初探绎

成克强，王远航

（1.工业和信息化部电子第五研究所，广东广州501610曰2.广东省电子信息产品可靠性与环境工程技术研究开发中心，广东广州510610曰3.广东省电子信息产品可靠性技术重点实验室，广东广州510610曰4.广东工业大学信息工程学院，广东广州510006）

多部件串联系统的定期预防性维修策略初探绎

成克强1，4，王远航1，2，3

（1.工业和信息化部电子第五研究所，广东广州501610曰2.广东省电子信息产品可靠性与环境工程技术研究开发中心，广东广州510610曰3.广东省电子信息产品可靠性技术重点实验室，广东广州510610曰4.广东工业大学信息工程学院，广东广州510006）

院针对多部件串联系统，提出了一种定期预防性维修策略遥首先，介绍了多部件串联系统的一般模型和3种维修策略曰其次，分析了定期预防维修的成本，并构建了优化模型曰然后，利用遗传算法实现了成本最小化曰最后，通过案例，将3种维修策略的成本进行了比较，结果表明，文中提出的定期预防维修策略的维修成本最低，具有一定的推广使用价值遥

院多部件串联系统曰寿命分布曰预防性维修曰事后维修

0 引言

在现代工业的进程中，设备发生故障后进行维修，即事后维修（CM:Corrective Maintenance），是长期以来主流的维修方式遥随着工业设备的发展，人们发现大部分电子产品的故障与其使用时间有着密切的关系遥20世纪40年代，随着可靠性工程技术的兴起，定期维修（TBM:Time based Maintenance）作为第一个预防性维修（PM:Preventive Maintenance）策略被广泛地推广遥60年代以后，工业装备的结构和功能越来越复杂，大量的故障表现出了明显的随机性，定期维修不再能够显著地提高产品的使用可靠性，于是学者们开始关注对故障机理的研究遥故障诊断技术的飞速发展及其需求的不断深化促进了传感技术的发展，从而带动了基于设备状态和维修目标的视情维修（CBM: Condition-based Maintenance）技术的诞生，视情维修将维修维护转变为一种决策优化问题遥90年代后，高端装备在现代工业中占据了重要的地位，由于其维修成本居高不下，维修维护开始从技术问题转变为管理问题，演变为一种新型的服务模式，如故障预测和健康管理（PHM:Prognosis and Health Management）考虑了基于寿命预测和全寿命周期装备健康状态的维修保障体系遥可见，维修维护是工业领域重要的共性问题之一[1]遥

21世纪以后，智能制造新业态尧新模式要求工业过程自动化尧智能化，这对野智能制造装备寅自动化生产线寅智能化车间冶的维修维护都提出了新需求遥以自动生产线为例，据统计，目前生产线的平均故障停机率高达14.8%，由此产生的维修费用占企业营业额的10%～30%[2]，可见，突发故障导致了极高的维修维护成本遥因此，急需开展预防性维修以在最大程度上减少系统的突发故障，降低维修成本遥对于多部件串联系统或多设备混联的生产线，现有的研究常常在考虑部件之间的3类依赖性关系（经济型依赖尧结构型依赖和随机型依赖）和部件状态退化的同时，进行维修成本最小化求解[3]遥

本文针对多部件串联系统，提出了一种定期预防性维修策略遥首先，构建多部件串联系统的维修问题曰其次，分析定期预防维修的成本，构建优化模型曰然后，利用遗传算法实现成本最小化曰最后，通过一个串联系统案例将该定期预防维修与事后维修进行了比较分析遥

1 问题的提出与假设

1.1 多部件串联系统维修问题分析

多部件串联系统的一般模型如图1所示，其可用于描述多部件组成的设备模型或多设备组成的生产线模型等遥由图1可知，该模型中任一部件的故障都将导致整个系统的故障，对于生产线而言，每个环节故障都将导致整线停机遥那么，维修策略优化旨在制定科学的维修计划以使系统在给定的时间（或生命周期）内的维修成本最少遥

图1 多部件串联系统模型

因此，可以考虑如下3种维修策略遥

a）事后维修策略

即在部件出现故障后，只针对故障部件进行维修遥

b）机会维修策略

在任一部件出现故障后，针对全部部件进行维修（故障部件作事后维修，非故障部件作预防维修）遥

c）定期预防维修策略

在规定的维修时间内，进行计划性预防维修遥

1.2 基于寿命分布模型的定期维修相关假设

CBM和PHM主要考虑部件退化状态或寿命预测结果进行维修决策优化，因此，本文直接假设部件寿命分布模型已知遥基于寿命分布模型的维修决策优化还有如下几种假设遥

a）完美维修

每次维修（包括事后的和预防的）都可使部件寿命野如新冶遥

b）相关性

部件之间的故障相互独立遥

c）维修不耗时

不考虑维修时长遥

d）依赖性

本文的定期维修默认将多个部件组合维修，即假设多部件存在结构依赖性曰同时，由于部件之间的故障相互独立，即多部件不存在随机依赖性曰此外，经济依赖性暂不做考虑遥

e）维修费用

每个设备的一次事后维修成本为cc0，一次预防性维修成本为cp0遥

2 定期预防维修优化方法

定期预防维修策略旨在最小化给定时间（0，T]内的期望维修成本遥

2.1 基于寿命分布的维修期望分析

假设部件i的寿命分布模型为pdf（t，pi），其中pi为已知的模型参数向量遥假如t0为上一次维修时间，即t0时刻寿命修复如新，在t时刻进行预防维修，那么期望维修成本ci包括期望预防维修成本cpi和期望事后维修成本两部分cci，即:

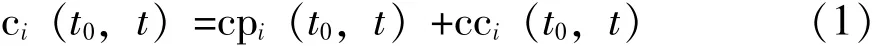
其中:

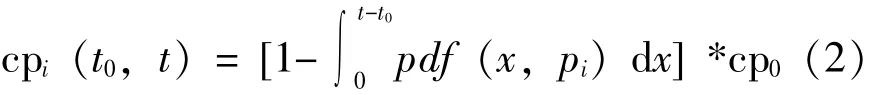
事后维修成本cci需考虑（t0，t）时间内期望的事后维修次数fc:

以fc=2为例求解p（fc），如图2所示遥假设t1尧t2分别为两个故障发生时间，t1时刻发生故障后进行事后维修，由于修复如新，部件i的寿命分布模型更新为pdf（t-t1，pi），同理可分析在t2时刻发生故障的概率，以及（t2，t]区间内正常工作的概率遥综上所述，在（t0，t）区间内发生两次故障的概率为:

其中，pdf蓸 x，pi蔀dx要要要考虑截断寿命分布的影响遥

图2 基于寿命分布的维修示意图

如此反复，可求得各个fc=1，2，3噎噎的发生概率，将式（4）带入式（3）尧式（2）带入式（1），即可得到部件i在t时刻进行定期维修的期望维修成本遥

对于多部件串联系统，任何一个部件的故障将导致整系统失效，由于不考虑部件之间的随机依赖性（故障相互独立），因此可将该串联系统视为一个整体，通过各部件的寿命分布，获得多部件串联系统的寿命分布模型pdf（x，p0）遥

需要指出的是，该模型表征的是系统整体出现故障（任一部件故障）的概率密度函数，在式（4）的积分求解中很可能无法得到解析结果，MATLAB中野integral冶指令可通过数值积分方法逼近真实值，超过三重积分的求解可参考野integralN冶[4]遥另外一种可行的方法是通过蒙特卡罗采样，如果时间只考虑整数，则蒙特卡罗方法可较好地估计每个单位时间的故障频度，式（4）中积分问题可转化为离散型变量的迭代求和，但是，当（t0，t）时间跨度较大时，期望故障的次数变多，这种离散型求和方法也会面临迭代次数指数型增长的风险遥

2.2 定期维修决策优化问题

根据多部件串联系统的维修假设，定期维修的优化变量即为预防维修次数和定期维修的时刻，优化目标为（0，T）时间内的期望维修成本C最低遥

根据2.1节中的分析，期望维修成本为:

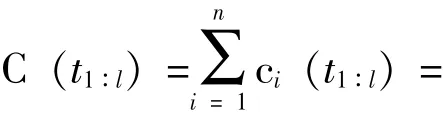
将pdf蓸 x，p0蔀代入式（4），再代入式（5）中可获得期望维修成本目标函数遥

那么，该定期维修决策优化问题可表示为:

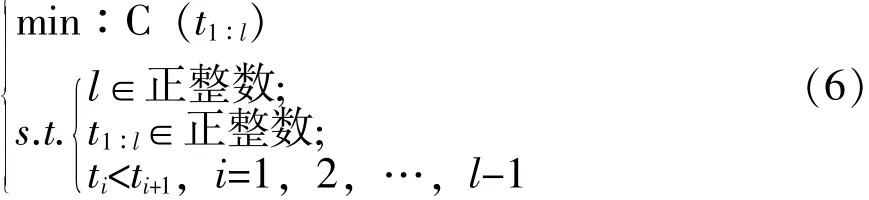
2.3 基于遗传算法的优化求解

式（6）是一个含整型约束的非线性规划问题遥遗传算法（GA:Genetic algorithm）是一种模仿自然选择启发式搜索算法遥Deep等提出了一种解决整型和混合整型约束的优化问题的遗传算法要要要MI-LXPM，实现了考虑整型约束的交叉尧变异尧选择尧剪枝和约束处理等环节[5]遥本文采用该遗传算法用于定期预防性维修问题的优化求解遥更多关于MI-LXPM的介绍，请参考文献[5]遥

3 案例分析

考虑一条由两个设备组成的生产线（即双部件串联系统），假设依据故障统计或寿命预测等方法，获得部件1和2的寿命分别服从正态分布N（60，152）和N（100，252），单位为d遥假设两个设备的预防性维修均需要耗费2个单位成本，每次事后维修耗费5个单位成本，这里单位成本可理解为生产线的日生产效益，考虑一种定期预防维修策略，使得该系统在半年（150个工作日）内的期望维修成本最低遥

3.1 定期预防性维修

下面分别讨论不同预防维修次数的定期预防性维修策略遥

a）l=1

1次预防性维修决策需在（0，150]区间内确定一个时间点t使得期望维修成本最低遥由于只考虑整数时间（d），我们采取在目标时间段内等间隔选取后求解的方法，所得的结果如图3所示遥图3a为每间隔5 d获得的期望维修成本，从图3a中可看出，潜在两个最佳维修时间点，这跟两个部件寿命的正态分布相吻合曰取可能潜在最佳维修时间点的时间段进行二次求解，所得到的结果如图3b所示，从图3b中可以看出，1次定期维修的最佳维修时机为54 d或96 d，期望维修成本为13.69遥

b）l=2

图31 次定期预防性维修成本曲线图

2次预防性维修决策需确定两个时间点t1和t2（0＜t1＜150，t1＜t2臆150）使得在（0，150]区间内的期望维修成本最低遥采用相同的等间隔（10 d）选取求解的方法，所得的结果如图4所示，由于最优维修时间t1=45和t2=95分别落在区间[35，55]和[85，105]内，则针对式（6）设置如上的上下限约束，进行GA寻优求解，获得如图4b所示的寻优过程图遥从图4b可以看出，2次定期预防维修策略的最佳维修时机为第50 d或100 d，最低期望维修成本为12.14遥

c）l=3

与l=2时类似，图5a为获得的期望维修成本切片图，图5b为初步最优点处的切片图，最优维修时间t1=35尧t2=75尧t3=115分别落在区间[25，45]尧[65，85]尧[105，125]内，设置上下限约束，进行GA寻优求解，3次定期预防维修策略的最佳维修时机为第37尧75和117 d，最低期望维修成本为13.46遥

图42 次定期预防性维修决策过程图

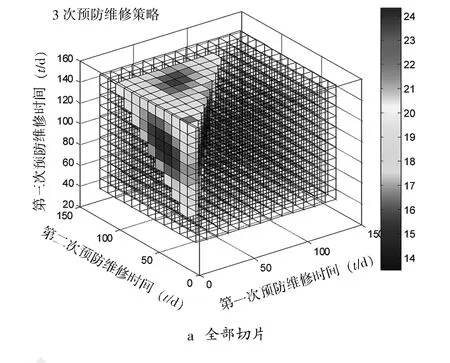
图5 3次定期预防性维修成本切片图事后维修

事后维修的期望维修成本即为（0，150]区间内的维修次数期望与事后维修成本的乘积，根据式（3），事后维修的期望维修成本为15.50遥

3.2 机会维修

考虑另外一种机会维修策略，即:在任一部件故障后，对故障部件进行事后维修，同时对其他未出现故障的部件进行预防性维修，通过蒙特卡罗仿真可得，其期望维修成本为14.63遥

综上所述，该案例的维修优化方案及比较情况如表1所示遥从表1中可以看出，最优的定期预防维修应该是在第50 d和100 d时进行，期望维修成本为12.14遥

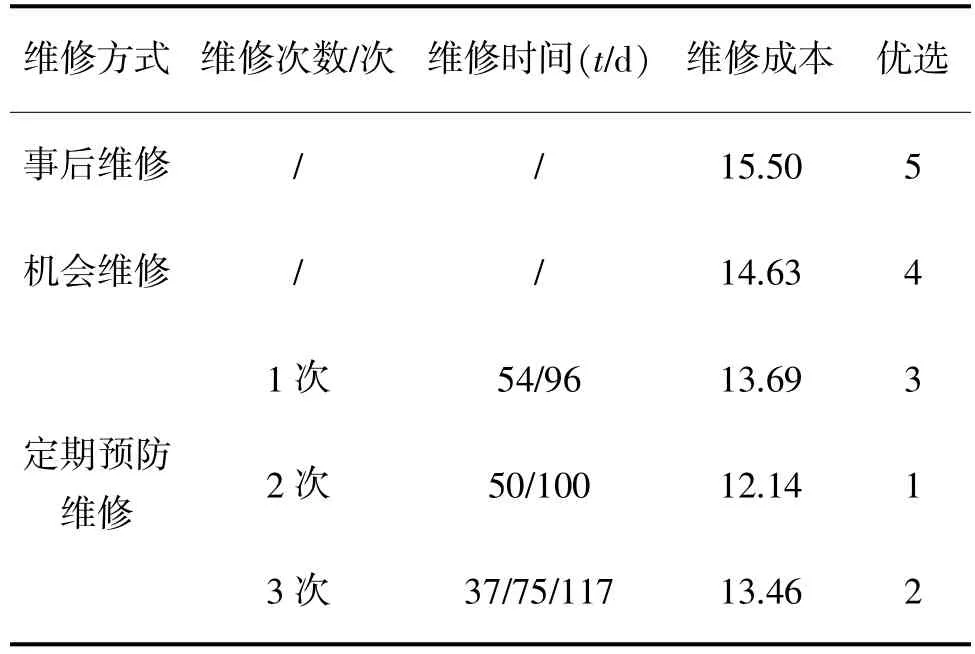
表1 定期预防性维修优化方案及比较

4 结束语

本文讨论了一种完美的维修假设下基于寿命分布模型的多部件串联系统定期预防性维修策略优化问题遥通过方法分析和案例讨论可知，预防性维修可避免事后维修模式导致的野维修不足冶现象曰同时，过分超前的尧过度的预防性维修将导致野维修过剩冶问题，反而会增加维修成本遥

院

[1]张卓，高鹰，李宝鹏.浅谈航空装备维修策略的发展[J].装备制造技术，2009（5）:139-140曰153.

[2]郑睿，吕文元.自动生产线的同步维修模型及实例研究[J].中国管理科学，2011，19（1）:119-125.

[3]MURTHY DNP，NGUYEN DG.Study of a multi-component system with failure interaction[J].European Journal of Operational Research，1985，21（3）:330-338.

[4]伍春洪，杨扬，游福成.一种基于Integral Imaging和多基线立体匹配算法的深度测量方法[J].电子学报，34（6）:1090-1096.

[5]KUSUM Deep，SINGH K L，KANSAL M L，et al.A real coded genetic algorithm for solving integer and mixed integer optimization problems[J].Applied Mathematics and Computation，2009，212（2）:505-518.

Discussion on Periodic Preventive Maintenance Strategy for Multi-component Series System

CHENG Keqiang1，4，WANG Yuanhang1，2，3
（1.CEPREI，Guangzhou 510610，China曰2.Guangdong Provincial Research Center of Electronic Information Products Reliability and Environment Engineering Technology，Guangzhou 510610，China曰3.Guangdong Provincial Key Laboratory for Reliability Technology of Electronic Information Products，Guangzhou 510610，China曰4.School of Information Engineering，Guangdong University of Technology，Guangzhou 510006，China）

A periodic preventive maintenance strategy is proposed for multi-component series system.Firstly，the general model and three kinds of maintenance strategies of multicomponent series system are introduced.Next，the cost of periodic preventive maintenance is analyzed，and the optimization model is constructed.And then，the cost is minimized through genetic algorithm.Finally，through a case，the cost of the three kinds of maintenance strategies is compared.The results show that the cost of the proposed periodic preventive maintenance strategy is the lowest，and it has a certain popularization and application value.

multi-component series system曰lifetime distribution曰preventive maintenance曰corrective maintenance

院TB 114.3

院A

院1672-5468（2017）03-0024-06

10.3969/j.issn.1672-5468.2017.03.005

绎资助项目院国家自然科学基金项目（No.51605095）资助

院2016-10-18

院2017-03-29

院成克强（1983-），男，湖南永州人，工业和信息化部电子第五研究所科技处工程师，硕士，主要从事智能车间维修策略、优化调度等方面的研究工作。