不同细观力学方法预测高聚物粘结炸药有效模量的比较

王竟成， 罗景润

(中国工程物理研究院 总体工程研究所， 四川 绵阳 621900)

不同细观力学方法预测高聚物粘结炸药有效模量的比较

王竟成， 罗景润

(中国工程物理研究院 总体工程研究所， 四川 绵阳 621900)

高聚物粘结炸药(PBX)不同于普通颗粒增强复合材料，其颗粒含量超过85%，组分弹性模量相差3～4个数量级，导致其有效模量的细观力学理论预测出现很大偏差。结合有限元细观模拟，对Mori-Tanaka法、自洽法、微分法3种细观力学方法的预测结果进行了比较分析。结果表明：界限法上下界之间有量级上的差异；当颗粒含量小于10%，颗粒间相互作用较小，不同方法计算的有效模量差异不大；含量大于20%时，颗粒间相互作用增强，3种解析法预测的结果逐渐出现差异，而微分法与有限元结果比较接近；当颗粒含量为94.9%，微分法预测的PBX杨氏模量比实测值高3.7%，Mori-Tanaka法和自洽法结果都有量级上的偏差；对于颗粒含量高、组分性能反差大的复合材料，微分法较合理地计及了颗粒间的相互作用，能较准确地预测其有效模量。

兵器科学与技术； 细观力学； 高聚物粘结炸药； 有效模量； 有限元； 微分法

0 引言

高聚物粘结炸药(PBX)广泛运用于军事领域，包含约90%的炸药颗粒(奥克托今(HMX)、黑索今、梯恩梯等)，它们之间用高聚物粘接。细观层次上可以将其划归为高密度颗粒填充复合材料，具有复杂的微细观结构，分为基体相和颗粒相。PBX不仅是一个功能构件，在加工、运输、储存等过程中还要承载一定的外力载荷，其有效力学性能引起广泛关注[1]，而有效模量[2-5]则是最基本的力学参量之一。由于PBX不同于普通颗粒增强复合材料，炸药颗粒杨氏模量高于粘结剂基体3～4个数量级，泊松比相差近1倍，加之其颗粒含量极高，颗粒间相互作用强烈，这些都对基于细观力学理论方法计算PBX的有效模量提出了巨大挑战。经典细观力学方法对PBX的适用性问题值得研究，而国内外也鲜有相关研究报道。

细观力学利用多尺度的连续介质力学理论和方法，研究材料细观结构和宏观性能间的定量关系，预测材料的有效弹性模量、热膨胀系数和强度等宏观性能。细观力学方法计算复合材料的有效模量已有半个多世纪的历史，广泛应用于各类复合材料：混凝土、金属基复合材料、高聚物复合材料等，分为界限法和解析法。Voigt模型和Reuss模型分别考虑均匀应变和均匀应力边界条件，根据最小势能原理和最小余能原理得到有效刚度的V-R上下界；采用Hashin-Shtrikman (HS)变分原理适当地选择均匀参考材料的刚度和极应力场，得到非均匀材料有效刚度的HS上下界。解析法主要以特征应变(Eshelby)问题的解答与等效夹杂理论为基础，假设椭球形颗粒和基体均为各向同性材料，选择不同的参考应变和参考刚度推导预测复合材料有效性能的公式，主要有稀疏法，Mori-Tanaka(MT)法，自洽(SC)法，微分(differential)法等[6]。

同时，经典的细观力学方法在各个领域不断地应用和发展，卢子兴等[7]利用四相球模型对复合泡沫塑料的模量和屈服强度进行了理论预测；沈珉等[8]采用MT法与稀疏法结合内聚力模型对含非理想界面的颗粒增强复合材料的有效模量进行了理论估计；胡更开等[9]总结了细观力学建立非均质材料有效性质的方法、主要结果和最新进展。对于颗粒含量极高、组分弹性模量相差几个量级的PBX材料，其有效模量的细观力学预测方法尚需研究。本文结合有限元法，研究了界限法和MT法、SC法、微分法3种经典细观力学方法预测PBX有效模量的适用性。

1 细观力学方法预测的对比

计算中炸药颗粒和粘结剂均视为各向同性的弹性体，炸药颗粒选用HMX，粘结剂选用聚酯型聚氨酯(Estane)。材料参数见表1，粘结剂基体和炸药颗粒的弹性性能有巨大的差异，泊松比ν相差1倍，杨氏模量E更是相差4个数量级。通过(1)式可进一步计算出体积模量K和剪切模量G.

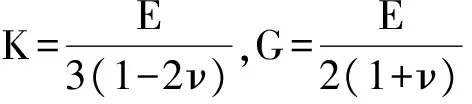
. (1) 表1 PBX组分弹性参量[10]Tab.1 Elastic properties of PBX ingredients

细观力学方法分为上下界限法和解析法。由于HS变分原理的条件比最小势能和最小余能原理强，(3)式HS上下界相较于(2)式V-R上下界给出了较精细的范围。

(2)

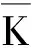
(3)

式中：c表示颗粒的含量；K0与G0为粘结剂的体积模量与剪切模量；K1与G1为炸药颗粒的体积模量与剪切模量。

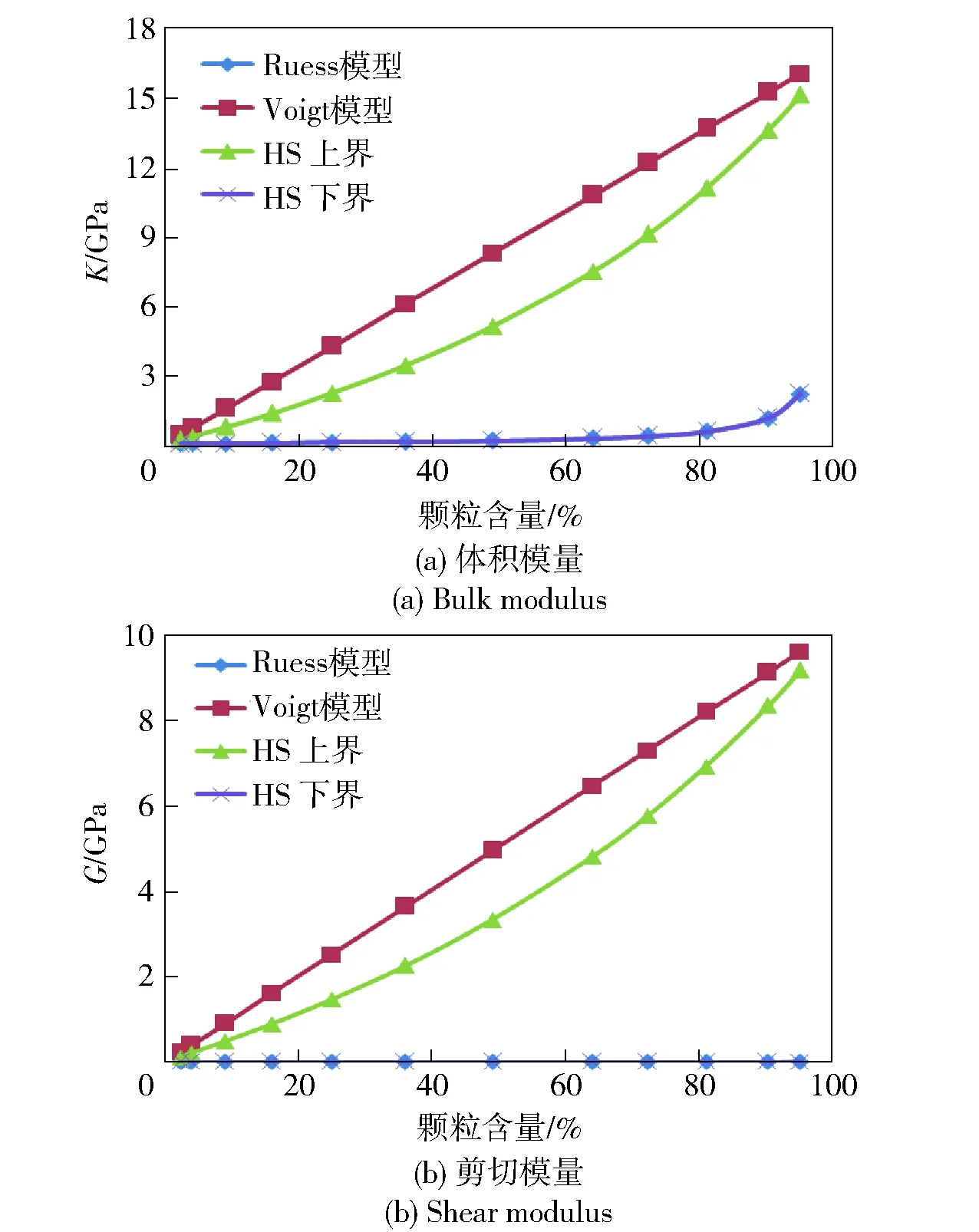
图1 HS上下界和V-R上下界的对比Fig.1 Comparison between HS bounds and V-R bounds

图1给出了不同含量下这两种界限法预测的体积模量K和剪切模量G. 从图1可以看出，HS上下界在V-R上下界之间，因此在后续的对比中，仅参考HS上下界。由于组分的材料参数相差巨大，无论是基于串并联模型的V-R界限法，还是通过选取不同组分的刚度作为参考刚度的HS界限法，上下界之间的差别都非常大，并且差异随颗粒含量的增加不断增大。因此，上下界限法不能用来预测PBX材料的有效模量，不过它们可以用来界定其他方法的合理性。

经典的解析法中，稀疏法没有考虑夹杂之间的相互作用，仅适用于夹杂含量很低时有效模量的预测，其他细观力学方法则通过不同程度地考虑夹杂间的相互作用，提高颗粒增强复合材料有效模量的估计值。(4)式MT法通过将远处应力(应变)改为基体平均应力(应变)，考虑了颗粒之间的相互作用，通过将局部集中张量转换为整体集中张量的方式提高有效模量。

(4)

(5)式SC法假定把夹杂物嵌于弹性模量未知的等效介质之中，通过提高参考刚度的方式提高有效模量的估计。

(5)

(6)式微分法沿用SC法的思想，将高颗粒含量复合材料的形成划分为诸多稀疏颗粒投入等效介质的过程，一定程度上弱化了SC法中有效模量的提高。

(6)

MT法给出了复合材料有效刚度简单明了的显示形式，而SC法的隐式方程组和微分法的非线性微分方程组都需要借助数值方法才能求解。此外，还有基于三相球模型的广义自洽法，由于其求解剪切模量过于冗长复杂的方程组，这里不加以列举。

利用(7)式可进一步计算出杨氏模量和泊松比为

(7)

图2显示了不同细观力学方法计算的有效模量，MT法与微分法的趋势基本一致，接近HS的下限值，可以证明MT法和HS下限的结果完全相同。SC法在颗粒含量c=50%附近脱离下边界，开始向上边界靠近。当含量为90%时，SC法计算的K值是MT法和微分法预测值的11倍左右，G值更是高达上百倍，这主要是由组分间弹性性能的巨大差异导致。将图2中低含量部分放大后(见图3)发现：尽管不同方法体积模量K的预测值比较一致，但剪切模量G从c=20%附近即分散开来，且差异逐渐增大；其中，SC法预测值最大，MT法最小。

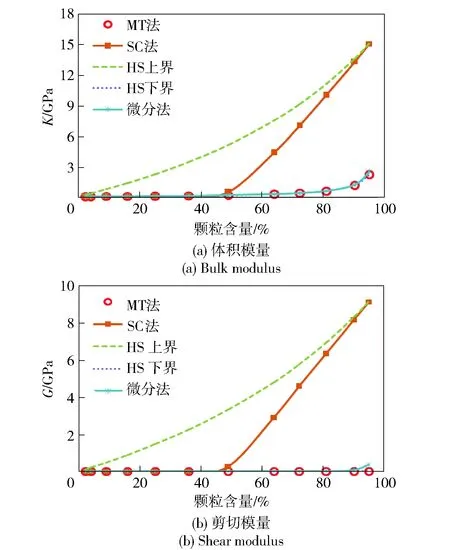
图2 不同细观力学方法计算的有效模量Fig.2 Effective moduli estimated by different methods

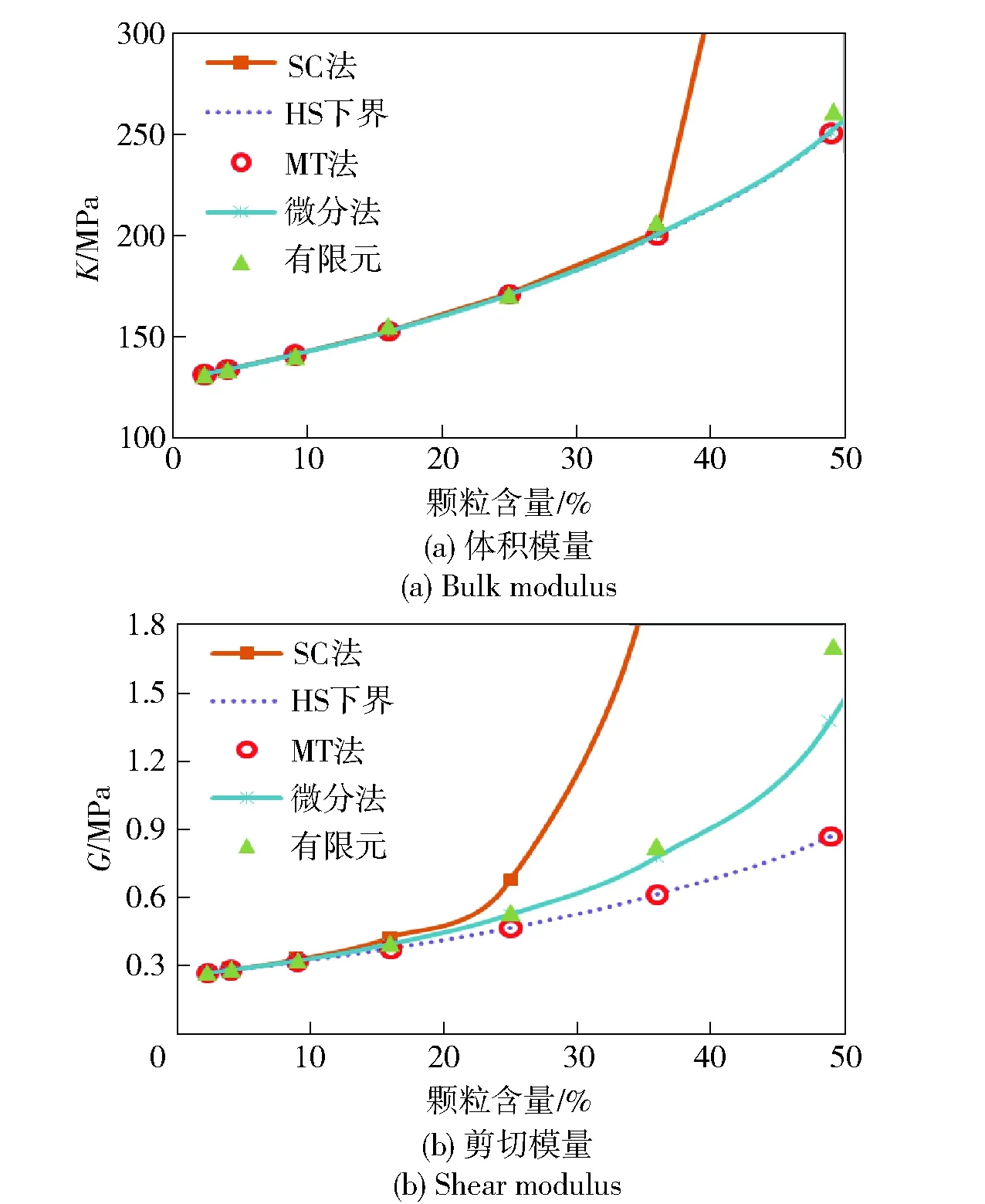
图3 不同方法计算值的分离Fig.3 Separation of estimates among different methods

2 有限元细观模型及计算方法

有限元是解决细观力学问题主要的数值方法，可以更精确地描述材料的细观几何结构，计算更复杂的力学行为。Ananda等[10]采用内聚力模型研究了PBX多种颗粒形貌和粒径分布的细观热力响应；戴开达等[11]通过建立炸药颗粒圆形随机模型和六边形模型，研究了粘结剂和颗粒性质对PBX有效弹性模量的影响；Biswajit等[12]采用循环单元法(RCM)和传统有限元法对PBX9501的有效模量进行了分析计算。

有限元细观模拟中，通常以代表性体积单元(RVE)为基础，将整个宏观结构视为由许多这样的体积单元按周期排布组合而成，通过施加均匀位移边界条件，提取RVE的形变和反力等信息，计算出RVE的有效弹性模量等。

考虑到真实炸药颗粒的平均尺寸在100 μm左右，选取RVE尺寸为1 000 μm×1 000 μm的方型区域[13-14]。由于圆形颗粒的填充度难以达到80%，基于Voronoi法构建不规则多边形颗粒模型对PBX的有效模量进行计算。Voronoi模型(见图4(a))可以使颗粒含量达到95%以上，并且与PBX真实细观形貌(见图4(b))有较好的相似性。通过改变粘结剂层的厚度，能方便地构建不同含量下的Voronoi模型。

图4 Voronoi 模型和PBX真实细观形貌Fig.4 Voronoi model and PBX microstructure

值得注意的是，有限元模型的构建是为了预测不同颗粒含量下有效模量的变化趋势，仅作参考使用。Voronoi模型采用的是不规则多边形颗粒，而经典的细观力学方法假设的是圆球形夹杂，因此，它们的预测值必然有差别。低含量下颗粒形貌对复合材料的有效性能影响不大，但随着颗粒含量的增加，颗粒形貌的影响便会凸显。除了借助有限元方法来模拟材料的力学行为，相关计及颗粒形貌的细观力学方法更值得不断发展完善。

有限元计算采用文献[11]中的方法，左边界和下边界分别约束住x向和y向位移，为保证边界节点的位移与边界线平行，在模型的上边界和右边界进行耦合约束；同时，在上边界节点施加y向位移来模拟单轴压缩试验。同样采用表1中的材料参数，使用平面应变假设和plane183单元进行有限元计算。根据平面应变假设和边界条件：

(8)

可得

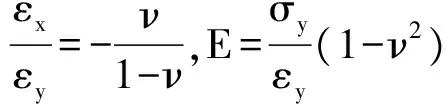
(9)

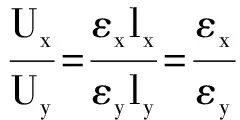
(10)

式中：εx、εy分别为x方向、y方向上的应变分量；σx、σy、σz分别为x方向、y方向、z方向上的应力分量；Ux、Uy分别为x方向、y方向上的位移分量；lx和ly分别为x方向和y方向RVE的边长。

根据文献[15]，平均应力既可以使用体积分得到，也可以使用面积分得到

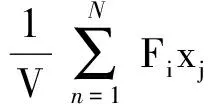
(11)

式中：F代表作用反力；N为RVE边界上节点的个数；V代表整个计算域；t为面力；x为节点间距。对于当前二维问题，有

(12)

式中：Fr为有限元后处理中提取的上边界的节点反力之和；l=1 000 μm.

考虑(9)式、(10)式、(12)式有

(13)

利用(1)式进一步求解出K和G.

3 结果及分析

表2列出了c<50%时有限元模型与细观力学方法的计算结果，有限元结果在图3中用三角形表示。当颗粒含量小于10%，颗粒之间的相互作用很小，各细观力学方法计算结果都具有很高的精度，而此时颗粒形貌的影响可以忽略，有限元结果与解析法计算结果吻合，体积模量计算误差小于1%，剪切模量计算误差小于3%，证明了有限元计算结果的可靠性。由于组分材料性能的巨大差异，当颗粒含量大于20%，各细观方法计算的剪切模量出现明显差异，且随着含量的增加，它们与有限元结果的偏差越来越大。从图3不难发现，微分法与有限元结果最接近，SC法与MT法的计算结果都有较大偏差。

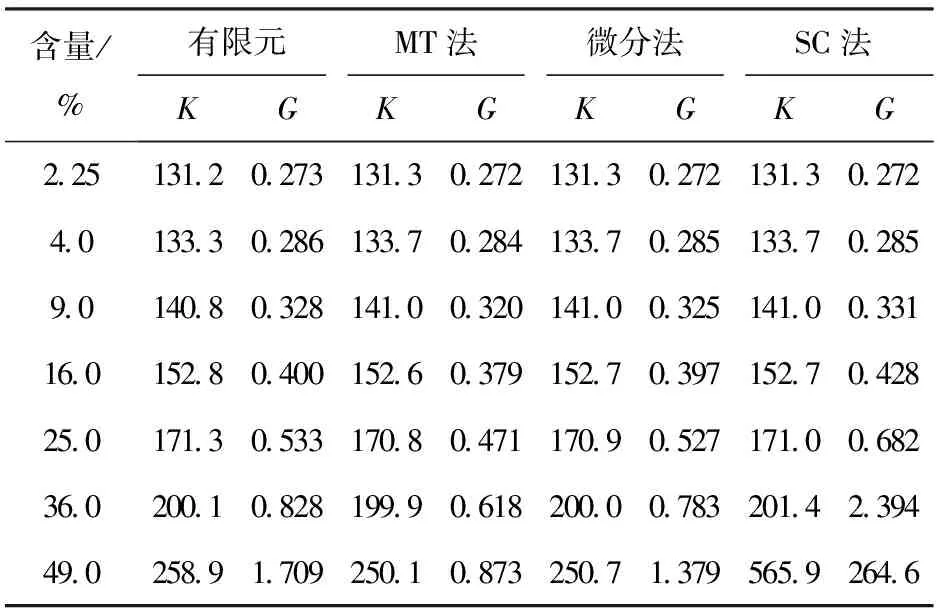
表2 c<50%时有限元结果与细观力学结果Tab.2 FE results and micromechanical results for c<50% MPa

表3列出了c>50%时有限元模型与细观力学方法的计算结果，图5直观地给出了有效模量随颗粒含量的变化趋势。需要指出的是，由于SC法预测的有效模量太大，已不能在图5中显示，这也说明SC法不能用来预测PBX材料的有效模量。高含量下，微分法与MT法预测的体积模量与有限元结果很接近，但剪切模量仅有微分法与有限元结果较符合，SC法太大，MT法太小，与低含量的情况一致。随着颗粒含量的增加，微分法预测值同有限元结果的差异变大，这主要由颗粒形貌的不同引起。微分法基于圆球形夹杂推导，而有限元结果则由多边形颗粒模型计算。

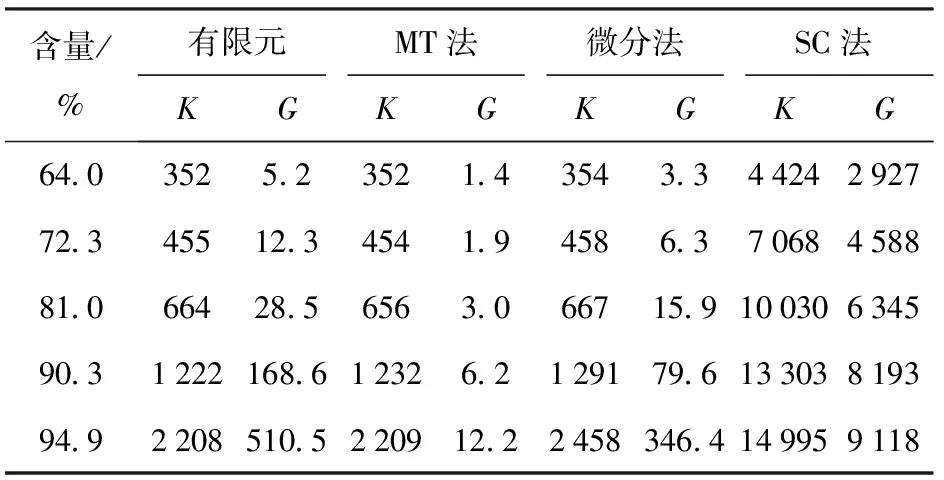
表3 c>50%时有限元结果与细观力学结果Tab.3 FE results and micromechanical results for c>50% MPa

图5 细观力学预测值与有限元结果的对比(c>50%)Fig.5 Comparison between micromechanical estimate and FE result (c>50%)

颗粒含量c=94.9%时，文献[16]给出了室温、准静态条件下PBX的杨氏模量为956.9 MPa±85.2 MPa. 利用(7)式分别计算c=94.9%时各种方法的杨氏模量，MT法为36.4 MPa，SC法为22.7 GPa，微分法为992.6 MPa. 由此可见，在颗粒含量很高时，3种细观力学方法的计算结果已有量级上的差异，这主要是因为炸药颗粒和基体粘结剂的弹性性能存在巨大差异。与实验数据相比，MT法低估了颗粒间的相互作用导致预测值太小，SC法则高估了颗粒间的相互作用导致预测值太大，微分法最接近(误差为3.7%)。以上结果表明，在预测颗粒含量高、组分性能反差大的复合材料有效模量时，微分法这种无穷次均匀化的方法较合理地计及了颗粒间的相互作用，其有效模量预测值比较准确。微分法最初用于研究悬浮液的性能，后来进一步发展用来预测复合材料的有效性能。其无穷次投放颗粒的过程理论上可以使颗粒含量无限趋近100%，因此，在计算高颗粒含量PBX材料的有效模量时仍较准确。

另外，在微分法基础上进一步引入颗粒形貌、尺寸分布等特征参量，能更精确地估测PBX的有效模量。

4 结论

1) PBX组分泊松比相差近2倍，杨氏模量相差4个数量级，界限法上下界之间出现量级上的差异，界限法不能有效预测PBX的有效模量。

2) 随着颗粒含量的增加，不同细观力学解析法预测的有效模量差异变大。当颗粒含量大于20%，微分法与有限元结果比较接近。

3) 微分法计算的PBX(c=94.9%)杨氏模量比实测值高3.7%，MT法和SC法都有量级上的偏差。因此，对于颗粒含量高、组分性能反差大的复合材料，微分法较合理地计及了颗粒间的相互作用，能较准确地预测其有效模量。

References)

[1] 罗景润. PBX的损伤、断裂及本构关系研究[D]. 绵阳：中国工程物理研究院，2001. LUO Jing-run. Study on damage, fracture and constitutive relation of PBX[D]. Mianyang: China Academy of Engineering Physics, 2001. (in Chinese)

[2] Biswajit B, Daniel O A. On predicting the effective elastic properties of polymer bonded explosives using the recursive cell methods[J]. International Journal of Solid and Structure, 2004, 41(2): 481-509.

[3] Biswajit B. Effective elastic moduli of PBX from finite element simulations[EB/OL].[2016-09-29].arXiv:cond-mat/0510367.

[4] 敬仕明，李明，龙新平. 基于改进的Hahin-Shtrikman方法预测PBX的有效模量[J]. 含能材料，2009, 17(6): 664-667. JING Shi-ming, LI Ming, LONG Xin-ping. On predicting effective elastic modulus of PBX by modified Hashin-Shtrikman model[J]. Chinese Journal of Energetic Materials, 2009, 17(6):664-667. (in Chinese)

[5] 敬仕明，李明，龙新平. PBX有效弹性性能研究进展[J]. 含能材料，2009, 17(1): 119-124. JING Shi-ming, LI Ming, LONG Xin-ping. Progress in predicting the effective elastic properties of PBX[J]. Chinese Journal of Energetic Materials, 2009, 17(1):119-124. (in Chinese)

[6] 黄克智，黄永刚.固体本构关系[M].北京：清华大学出版社，1999: 120-172. HUANG Ke-zhi, HUANG Yong-gang. Solid constitutive relations [M]. Beijing: Tsinghua University Press, 1999: 120-172. (in Chinese)

[7] 卢子兴，邹波. 复合泡沫塑料模量和屈服强度的理论预测[J].复合材料学报，2014, 31(4): 998-1005. LU Zi-xing, ZOU Bo. Theoretical prediction for modulus and yield strength of syntactic foams[J]. Acta Composite Material Sinica, 2014, 31(4): 998-1005. (in Chinese)

[8] 沈珉，郝培. 颗粒增强复合材料非理想界面刚度和有效模量的理论估计[J]. 复合材料学报，2016, 33(1): 189-197. SHEN Min, HAO Pei. Theoretical estimation of imperfection interfacial stiffness and effective modulus in particle reinforced composites[J]. Acta Composite Material Sinica, 2016, 33(1): 189-197. (in Chinese)

[9] 胡更开，郑泉水，黄筑平. 复合材料有效弹性性质分析方法[J].力学进展，2001,31(3): 361-393. HU Geng-kai, ZHEN Quan-shui, HUANG Zhu-ping. Micromechanics methods for effective elastic properties of composite materials[J]. Advances in Mechanics, 2001, 31(3): 361-393. (in Chinese)

[10] Barua A, Zhou M. A Lagrangian framework for analyzing microstructural level response of polymer-bonded explosives[J]. Modeling and Simulation in Materials Science and Engineering, 2011, 19(5): 1-24.

[11] 戴开达，刘龑龙，陈鹏万. PBX炸药有效弹性模量的有限元模拟[J].北京理工大学学报，2012, 32(11): 1154-1158. DAI Kai-da, LIU Yan-long, CHEN Peng-wan. Finite element simulation on effective elastic modulus of PBX explosives[J]. Transactions of Beijing Institute of Technology, 2012, 32(11): 1154-1158. (in Chinese)

[12] Biswajit B, Daniel O A. Micromechanics based determination of effective elastic properties of polymer bonded explosives[J]. Physica B, 2003, 338(1/2/3/4): 8-15.

[13] Lemaitre J. Formulation and identification of damage kinetic constitutive equations[J]. Continuum Damage Mechanics Theory and Applications, 1987, 295: 37-89.

[14] Ostoja S M. Random field models of heterogeneous materials [J].Solids and Structures, 1998, 35(19): 2429-2455.

[15] Nguyen V D, Bechet E, Geuzaine C, et al. Imposing periodic boundary condition on arbitrary meshes by polynomial interpolation[J]. Computational Material Science, 2012, 55(5): 390-406.

[16] Gray G T, Idar D J, et al. High- and low-strain rate compression properties of several energetic material composites as a function of strain rate and temperature [C]∥11th international Detonation Symposium. Snowmass, Colorado, US: Los Alamos National Laboratory, 1998.

Comparison of Effective Moduli of Polymer Bonded ExplosivePredicted by Different Micromechanical Methods

WANG Jing-cheng, LUO Jing-run

(Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621900, Sichuan, China)

Polymer bonded explosives (PBXs) are different from conventional particle reinforced composites. PBXs possess over 85% of particle volume fraction, and the elastic modulus of particle can be three or four orders of magnitude higher than that of binder. Large deviations are observed on the effective moduli predicted by micromechanical methods. The predicted results of several micromechanical methods for the effective moduli of PBX are analyzed based on finite element method. Results indicate that both Voigt-Reuss bounds and Hashin-Shtrikman bounds give rather large estimated regions; when particle fraction is less than 10%, the differences among the effective moduli estimated by the different methods are not obvious since the particle interaction is negligible; when particle fraction exceeds 20%, the estimated results of three analytic methods are different from each other gradually due to the enhancement in particle interactions, and the estimated results of differential method agree with those of finite element method. For the particle fraction of 94.9%, Young’s modulus calculated by differential method is only 3.7% higher than the experimental value of PBX, while a huge error occurs using Mori-Tanaka method or self-consistent method. For the composites that possess high particle fraction and strong contrast in their ingredient properties, the differential method provides better estimates of effective modulus owing to its relatively favorable evaluation on particle interactions.

ordnance science and technology; micromechanics; PBX; effective modulus; finite element; differential method

2016-10-19

国家自然科学基金项目(11472257)

王竟成(1991—)，男，博士研究生。E-mail：wangjczzy@sina.cn

罗景润(1966—)，男，研究员，博士生导师。E-mail：jrluo2000@vip.sina.com

TB332; O343.1

A

1000-1093(2017)06-1106-07

10.3969/j.issn.1000-1093.2017.06.009