多智能体网络在运筹学图与网络分析教学中的应用

何广

摘要：本文介绍如何巧妙地应用多智能体网络来解释运筹学图与网络分析教学中有关图的一些概念，比如：连通性，度，支撑树等，从而使得我们的教学更加生动与形象，同时也使得学生对这些概念的理解更加深刻。

Abstract： This paper introduces how to use multi-agent networks to explain some concepts related to map graphs such as connectivity， degree， support tree in the teaching of operational research map and networks analysis， which makes our teaching more vivid and image， and also makes students understand these concepts more deeply.

关键词： 联通图；支撑树；多智能体

Key words： connected graph；support tree；multi-agent

中图分类号：TB114.1 文献标识码：A 文章编号：1006-4311（2017）21-0238-02

0 引言

运筹学作为科学名字最早出现在20世纪30年代末，那时候的运筹学可以说就是战争的“工具”，当时中英美借助运筹学的思想，强有力的打击了德意日三国，为二战的胜利奠定了基础。二战胜利后运筹学被广泛的应用到工农业生产的各个领域，大大的提高了我们的生产效率，这也促使近几十年运筹学获得了空前的发展。图与网络分析作为运筹学的一个重要分支，现如今已被广泛的应用到物理、化学、控制论、信息论，科学管理、电子计算机等各个领域[1]。在实际生活、生产和科学研究中，有很多问题可以用图论的理论和方法来解决。因此在运筹学的教学中如何能够使学生更加深刻的理解图与网络分析就显得尤为重要。在该章节的教学中引用一些更实际的网络的例子来解释有关网络的概念无疑能够使教学更加生动易懂。而多智能体网络是近20年控制领域的研究热点[2]，利用多智能体网络来解释图的有关概念既能拓广学生的视野，又能使学生更容易理解，从而调动学生的学习积极性，进而使得我们的教学效果得到大幅度提高。

1 多智能体网络与图

众所周知，许多网络都可以看成是多智能体网络，如无人机网络，移动机器人网络，那么这些网络和图有什么关系呢？当我们把无人机抽象成顶点，两架无人机之间如果有信息交流就连一条边，这样无人机网络就可以看成一个图，如果我们这样去解释图能够使很多同学相信原来图真的可以包含很多复杂的内容，图真的可以和很多的实际问题产生密切的联系，从而激起同学学习图论的兴趣。

2 有向图与无向图

在图论中为什么要把图分成有向图和无向图呢？他们的区别的本质又在哪里呢？我们可以借助多智能体网络跟同学们这样解释：在有些无人机网络中信息的交流是相互的，无人机甲可以接收到向无人机已的信息，同时无人机已也可以接收到无人机甲的信息，即信息可以在这两架无人机之间共享互通，这样形成的图就是无向图；而在有些无人机网络中信息交流可能是单向的，无人机甲可以接收无人机已的信息，而无人机已却不能接收无人机甲的信息，这样形成的图就是有向图，如果我们能这样去解释有向图和无向图而不在拘泥于“单行线和双行线”，肯定能够使同学们对于有向图和无向图的理解更加深刻，也使之能够明白为什么非要把图分成有向图和无向图来进行研究。

3 连通性的概念与意义

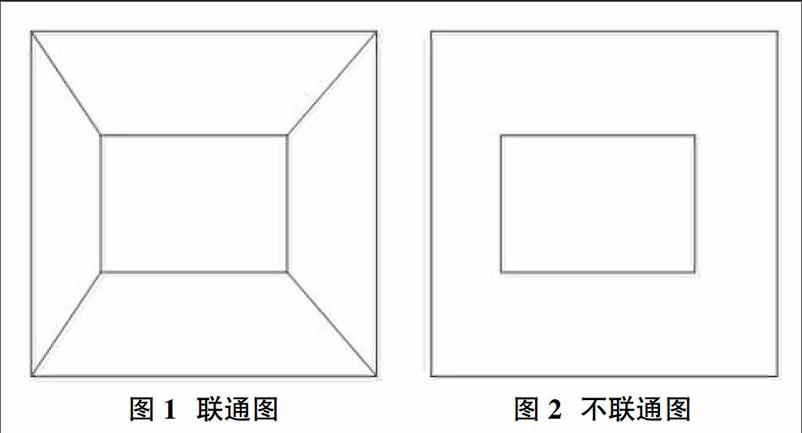
所谓图的连通性是指图中的任意两个顶点都是连通的，也即是任意两个顶点之间都存在一条初等链。而针对无人机网络，所谓连通性是指任意两个无人机即使两者之间不能进行直接的信息交流也能够借助其他的无人机进行间接的信息交流，从而实现信息的共享。

如图1的无人机网络就是一个联通图，而图2的无人机网络已就是不联通的。对于无人机网络来说连通性意味着什么呢？这意味着这个無人机网络可以实现网络一致性[3]，所谓网络一致性是指网络的一种集体行为，即每一个无人机的状态（或者说行为）可以趋近于一致，而多智能体网络的一致性问题是当今控制论领域研究的一个热点问题，这个时候学生会明白原来连通性背后隐藏着这么大的意义啊！同时也进一步的拓广了同学们的视野，使他们明白了图与网络分析在当今科学研究的前沿中起到了多么重要的作用，从而激起他们对图论学习的积极性。这时候我们可以诱导学生思考这样一个问题：在一个无人机网络中，整个网络时时刻刻都不是联通的，那么这个时候整个网络还能实现一致性吗？

比如整个网络可能在图3和图4两个网络中进行着随机切换，这两个网络都不是联通的，那么这个时候网络能实现一致性吗？

回答是肯定的。最新的研究结果表明，只要整个网络是“联合联通”的，网络就能够实现一致性[3，4]，而图3和图4的并就是图1，而图1是联通图，因此多智能体网络在图3和图4之间相互切换时，整个网络是可以实现一致性的。从而我们能够引入一个新的概念“联合联通”，所谓联合联通是指当整个网络在若干个拓扑结构上切换时，如果这些拓扑结构的并是一个联通网络，这时候就称随时间演化的网络是联合联通的。而“联合联通”这个概念在现在的大多数的运筹性的教科书中都没有出现，从而能够进一步的扩大学生的知识面。

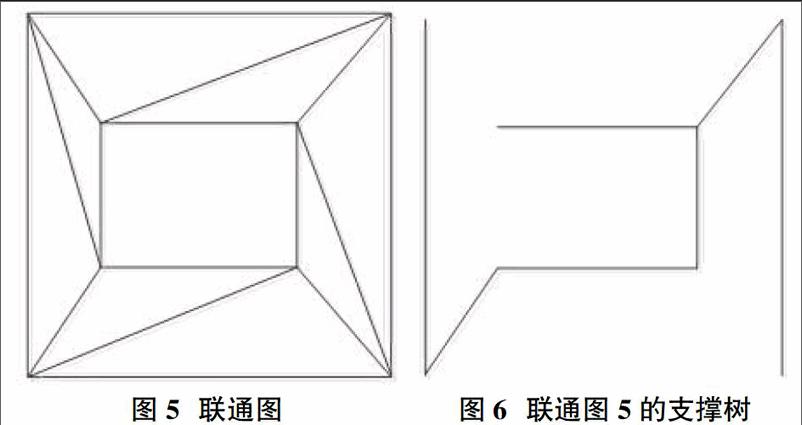
4 支撑树的概念与意义

在讲到支撑树的概念的时候我们可以先让同学们比较两个无人机网络图5和图6，问问同学们，这两个网络哪个网络可能更能够节约通信成本。从而我们能够引入树与支撑树的概念。使得学生能够明白要想实现网络一致性在联通性的基础上网络还可以进一步的简化，即网络图只要存在支撑树多智能体网络就能够实现一致性，从而求一个联通图的最小生成树就显得尤为重要，因为对于多智能体网络来说求一个联通图的最小支撑树问题就是节约通信成本的问题，在当今资源紧缺的情况下节约成本的意义是显而易见的。

实际上，在图论中的很多概念的讲解都可以借组多智能体网络，比如：度与连接矩阵的概念等，在这里就不一一叙述了。

5 结论

图与网络分析中的很多概念的讲解都可以借助多智能体这个实际网络，这样做不仅能够使问题变的通俗易懂，使学生对于概念的理解更加深刻，同时也拓广了学生的知识面，从而极大地提高教学效果。

参考文献：

[1] 钱颂迪，《运筹学》，清华大学出版社，1981.09.

[2]Georg S. Seyboth， Dimos V. Dimarogonas， Karl H. Johansson， Event based broadcasting for multi-agent average consensus， Automatica， 49：245-252，2013.

[3]Ali Jadbabaie， Jie Li， A. Stephen Morse， Coordination of groups of mobile autonomous agents using nearest neighbor rules， IEEE Transactions on Automatic Control， 48（6）：988-1000，2003.

[4]Wei Ren， Randal W. Beard， Consensus seeking in multiagent systems under dynamically changing interaction topologies， IEEE Transactions on Automatic Control， 50（5）：655-661，2005.