智能自动驾驶汽车的轨迹优化
2017-07-08李晓芳何俊
李晓芳++何俊
摘要: 智能自动化驾驶技术是一门新兴的技术,在汽车自动驾驶的过程中,如何让汽车避开障碍物并以最短的路径到达指定的位置,是智能自动化驾驶汽车的关键性问题。本文通过模拟智能自动驾驶汽车的运行环境,利用遗传算法对汽车的运行轨迹进行研究,实验证明可以获得较好的结果。
Abstract: Intelligent automation driving technology is an emerging technology. In the process of vehicle automated driving, how to let the car to avoid obstacles and to reach the location specified in the shortest path is key problem of intelligent automation vehicle driving. In this paper, through the simulation of the running environment of intelligent automatic vehicle driving, the genetic algorithm is used for vehicle trajectory study, and the experiments show good results can be obtained.
关键词: 智能自动驾驶汽车;遗传算法;轨迹优化
Key words: intelligent automation vehicle driving;genetic algorithm;trajectory optimization
中图分类号:U471.1 文献标识码:A 文章编号:1006-4311(2017)21-0129-02
0 引言
自动驾驶汽车又称无人驾驶汽车、电脑驾驶汽车或轮式移动机器人,是一种通过电脑系统实现无人驾驶的智能汽车。自动驾驶汽车技术的研发,在20世纪也已经有数十年的历史,于21世纪初呈现出接近实用化的趋势。自动驾驶汽车依靠人工智能、视觉计算、雷达、监控装置和全球定位系统协同合作,让电脑可以在没有任何人类主动的操作下,自动安全地操作机动车辆。
全局路径规划是指在环境信息全部已知的情况下,为智能自动驾驶汽车规划一条无碰最优路径。由于常用路径规划方法均存在一定的局限性,因此,目前智能自动驾驶汽车路径规划问题的研究重点在于寻求一些更加有效的求解方法或者在已有方法的基础上进行改进,以使其能够更好地解决路径规划问题。
1 遗传算法的基本理论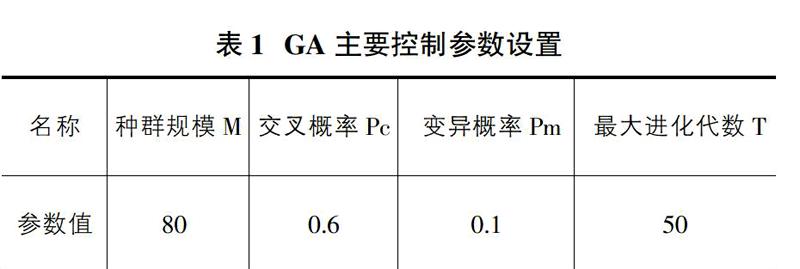
遗传算法的核心思想是借用遗传学中的思想以及达尔文进化论的“物竞天择,适者生存”,最早由美国密歇根大学的John Holland教授于1975年提出的,1989年,Goldberg在其著作中对遗传算法进行了更为全面和系统的总结,并由此奠定了遗传算法的基础。遗传算法是从某一初始解集出发,采用一个评价函数(也称为适应度函数)来评价每个个体的优劣,即个体对环境的适应程度,用作以后遗传操作的依据,经过选择、交叉和变异等遗传操作产生新一代的种群,然后对新的一代重复遗传操作,经过一定次数的迭代之后,最终收敛到问题的最优解或次优解。
2 自动驾驶汽车路径规划方法
2.1 环境模型的建立
环境建模是实现路径规划的基础,其目的是将实际的物理空间映射成算法能够处理的抽象空间。合理的环境模型有利于计算机存储、处理和更新以及减少搜索量。目前常用的环境建模方法主要包括:可视图法、栅格法、自由空间法和拓扑法,其中栅格法是使用较为成功的一种环境建模方法,本文将采用栅格法建立环境模型。
在A中建立直角坐标系XOY,其中坐标原点设在A区域的左下角,且和分别是在Xmax、Ymax轴上的最大值,对X,Y以智能自动驾驶汽车能自由运动的最大活动范围Ra为步长分别进行划分,由此形成工作栅格,其中每行的栅格数m=ceil(Xmax/Ra),每列的栅格数n=ceil(Ymax/Ra),最终构成一个m×n的栅格矩阵。假设环境中存在k个障碍物,则每个障碍物obi(i=1,2…,k)占一个或多个栅格,当不满一个栅格时,按一个栅格计算。
目前关于栅格的标识方法主要有以下两种:
①直角坐标法。
把(0,0)设为坐标原点,规定水平向右为X轴正方向,竖直向上为Y轴正方向,坐标轴上的单位长度为栅格大小,因此,任意一个栅格都可以用直角坐标(x,y)表示。
②序号法。
在建立的栅格模型中,定义从左上角开始的第一个栅格A(1,1)的序号为1,A(1,2)的序号为2,…,依次类推。
对于任意一个栅格A(a,b),其中a为在A中的行号,b为在A中的列号,都有确定的坐标(x,y)及相应的序号S与之一一对应, 在n×n的栅格环境中,栅格序号S和坐标(x,y)的关系为:
x=mod(S-1,n)+0.5y=n+0.5-ceil(S/n)(1)
式(1)中,mod为求余运算,ceil為向上取整运算。
另外,对智能自动驾驶汽车运行环境和智能自动驾驶汽车本身做出如下假设:
①智能自动驾驶汽车是长方形的,其最大尺寸为D,规划时不考虑智能自动驾驶汽车的高度;
②环境中障碍物的位置信息及智能自动驾驶汽车的起始点和目标点位置全部已知,不存在动态障碍物。
③将已知的静态障碍物边界向外扩展D/2,则智能自动驾驶汽车可用其中心点来表示,在规划过程中作为质点考虑。
2.2 适应度函数
适应度函数不仅反映了各条路径的优劣程度,而且对算法的收敛和稳定性都有较大的影响,此处适应度函数F以路径总长度的倒数作为评价标准,如下所示:
F=■(2)
式中n为该个体通过的栅格数目总数,di,i+1为节点i和节点i+1之间的欧氏距离。
2.3 遗传操作
2.3.1 选择操作
选择操作的设计目的在于保留好的基因个体,从而提高种群的质量。目前,常用的方法包括锦标赛选择法、轮盘赌法、最佳个体保留法和基于排序的选择法,然而不同的选择方法将会导致不同的选择压力,若选择压力较大,种群的多样性迅速减少,算法易出现早熟收敛现象;若选择压力过小,虽然可以维持种群的多样性,增大搜索到全局最优解的概率,但是又使得算法趋于随机搜索状态;因此,选择压力对算法的性能具有重要作用。
2.3.2 交叉、变异操作
交叉操作选用单点交叉方法,由于路径的不同而导致个体长度的不同,因此,对于所选择的两个个体,其交叉点的位置不一定相同,这里选取相同序号点处进行交叉(除S和G外),以保证路径的连续性。如果两个体具有相同序号的点不止一个,则任选其一进行交叉,如果无相同序号点,不进行交叉操作。交叉操作结束后,首先判断其子代中的每个个体是否包含相同序号点,若包含,则应删除相同点其中之一及其中间部分。
在变异过程中,由于所产生的初始种群均为连续路径,若采用随机变异操作将会产生间断路径,导致种群质量退化,为克服这一缺陷,本文采取对待变异个体随机删除一点(除S和G外),并把该点所在栅格标记为静态障碍物,再判断该个体是否为间断路径,如果是间断路径,则采用种群初始化的方法修补间断路径,以保证变异后路径的连续性。
3 实验结果及分析
为验证算法的正确性和合理性,本文运用Matlab软件在10×10的栅格环境模型下对该算法进行仿真,并与基本遗传算法进行比较。在基本遗传算法中,初始种群随机生成,选择算子采用轮盘赌法,算法的主要控制参数;在本文算法中的主要控制参数设置。其中S和G分别表示起始点和目标点。
通过多次实验,该算法在一般环境下的路径规划问题,具有较快的收敛速度,能够以很大的概率收敛到全局最优解;对于复杂环境下的路径规划,虽然收敛速度有所減慢,但最终也能够收敛于全局最优或近似最优解。
本文的计算方法获得了较好的轨迹。(表2)
4 总结
本文为了解决智能自动驾驶汽车的轨迹优化问题,首先采用栅格法建立自动驾驶汽车的工作环境空间,然后利用遗传算法对其进行优化,获得了较好的运行轨迹。
参考文献:
[1]王艺帆.自动驾驶汽车测试体系与现状探究[J].汽车与安全,2016(10).
[2]董长印.自动驾驶汽车下匝道路径优化控制策略研究[D].东南大学,2016.
[3]张星.基于麦克纳姆轮的全向AGV运动控制技术研究[D].重庆大学,2016.
