基于EMD的误差信号分解

，，，，，

(1.三峡大学电气与新能源学院，湖北 宜昌 443002；2.中国船舶重工集团公司第七一○ 研究所，湖北 宜昌 443002；3.国网咸宁供电公司，湖北 咸宁 437000)

1 引言

随着电力需求的迅猛增长以及电力系统的高速发展，电力行业面临着提高电力设备利用率，降低电力设备运行成本以及增强电力系统安全稳定运行的严重挑战[1]。作为电力系统重要组成部分的电气设备，尤其是大型高电压设备，如果发生突发性停电事故，会造成巨大的经济损失和不良的社会影响。

电力设备在线监测技术近几十年在国内发展非常活跃[2-3]，几大高校都设立了相应学科和实验室。在较早的在线监测系统研究中，人们主要集中在对单个电力设备某个参数的研究之中，比如较常见的如变压器局部放电在线监测系统或装置。在经历了这种单一、孤立式的研究之后，以多种电力设备为监测对象的综合性在线监测是发展的必然趋势，随着在线监测系统功能的增强和方式的多样化，其本身的复杂性也不可避免地增加，监测设备自身软硬件状况和所处的外界环境都会在很大程度上影响到监测的准确性和可靠性[4]。因此，对电力设备的误差进行分析就显得尤为重要。

2 经验模态法

2.1 EMD的提出

经验模态法(EMD)是由美国国家宇航局华裔工程师Huang在1998年创造性地提出[5]，此方法是一种新型的信号分析方法，能够良好地分解非平稳信号。经验模态法的分解过程完全是由数据的自身驱动，不需要采用信号的先验知识，能够根据自身的特征进行分解得出其基函数即本征模态函数(IMF)，具有很好的自适应性，而本征模态函数能够有效的反映出信号的频域以及时域特征，相比于前几种分析方法而言具有明显的优势。经验模态法为信号处理提供了新的思路与研究方向，是一种新型的自适应信号时频处理方法，其的提出在国内外都产生了很大的影响，引起各国学者的广泛关注和研究[6-7]。

2.2 本证模态函数

EMD分解法是将信号解为一系列本征模态函数与一个残余趋势项[8]。例如对于原始信号s(t)，其经过经验模态法分解后为:

(1)

对于每个IMF而言，其必须符合下述两个约束条件：

(1)在整个时间轴上，信号所含过零点和极值点的个数只有两种可能，一种完全相同，一种个数相差为一。

(2)对于信号的任意点，此点所对应的上包络线与下包络线的值均互为相反数，即两条曲线在任意点的和均为零。

Huang等认为EMD方法的分解过程需要满足以下三点假设：

(1)原始信号必须至少包含一个极大值点，一个极小值点；

(2)如果信号数据不存在极值点，但存在变形点，则可以通过一次或多次微分来获得极值点，然后再通过积分来获得分解结果；

(3)通过两个极值点设定的特征时间尺度可以确定待处理数据的局部时域特性。

2.3 EMD算法流程

EMD算法的基本原理是利用数据的特征时间尺度来获得本征模态函数，并进行数据分解。EMD方法所进行分解的过程，可以看成一种“筛选”的过程[9-11]。其具体步骤如下：

(2)

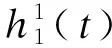
将c1(t)从信号x(t)中除去，则可获得一个新信号r1(t)

r1(t)=x(t)-c1(t)

(3)

将r1(t)进行上述分解直到产生一个新的IMF分量，记为c2(t)。重复此过程，可得到一系列的IMF分量，直到产生残余分量rn(t)为一个单调函数或常量时，则EMD分解过程到此为止，而原始信号x(t)被分解为多个IMF和一个残余趋势项之和：

(4)

3 EMD分解误差信号仿真实例

以图1所示的混联测量系统为例。

图1 混联式测量系统

令系统内部各模块之间的传递参数分别为：

(5)

同时确定各子模块所产生的相应的误差信号分别为：

(6)

假设不存在外界干扰信号，即nx(t)=0,ny=0，则最终的误差信号为：

eF=(e1(t)f2+e2(t))f3+e3(t)+e1(t)f4+e4(t)

(7)

原始信号如图2所示。

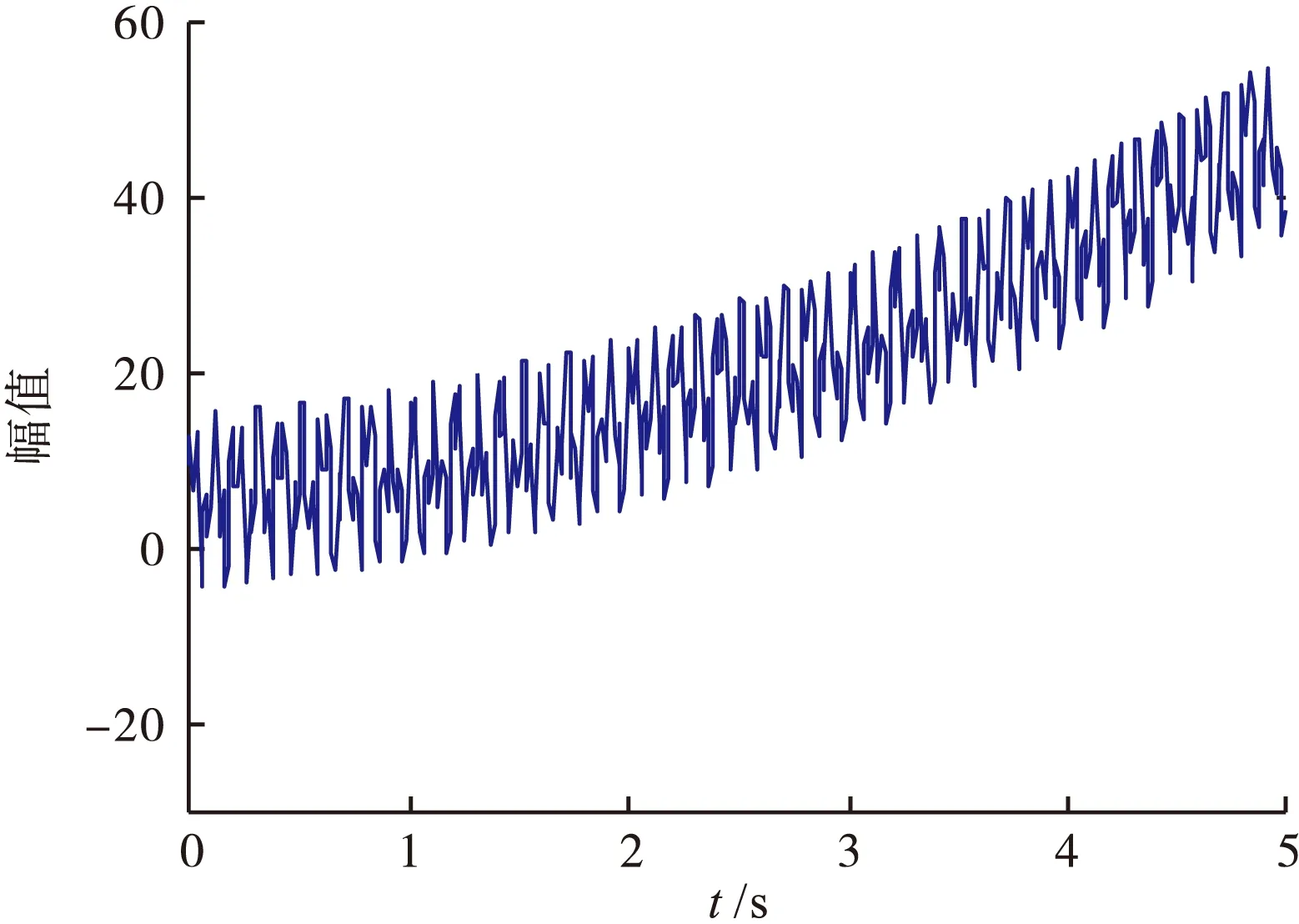
图2 原始信号

将此信号进行EMD分解结果如图3所示。

图3 EMD分解后的各信号分量

由图3可以看出EMD分解首先从信号中分解出高频分量，再逐步向低频分解直至残余分量为一个变化缓慢的趋势信号为止。由式(7)可以得出误差信号由三个频率各不相同的正弦信号以及一个一维二次信号共同组成，四个信号根据频率由高到低分别与EMD的四个分量成一一对应关系。EMD分解后产生的各个IMF分量虽然与动态误差信号之间存在微小差异，但是各个分量能够有效地表征动态误差信号各个频率分量。

4 结语

本文以电力在线监测设备为研究背景，发现问题，提出解决问题的方案。将EMD分解法应用于测量误差信号的分解，通过计算机仿真可以得出EMD方法能够有效地分解误差信号。针对误差子曲线进行分析，能够更加清晰的研究误差的特点以及各个子误差产生的源头，为电力在线监测设备的设计与制造提供良好的理论基础。

[1] 陈卓,刘念,薄丽雅.电力设备状态监测与故障诊断[J].高电压技术,2005,31(4):46-48.

[2]罗传勇.电气绝缘材料标准化现状与发展方向浅析[J].电气制造,2009(11):18-20.

[3]唐炬.防御变电设备内绝缘故障引发电网停电事故的基础研究[J].高电压技术,2012(6):1281-1291.

[4]Hoshino T,Maruyama S,Ohtsuka S,et al.Sensitivity comparison of disc-and loop-type sensors using the UHF method to detect partial discharges in GIS[J].Dielectrics & Electrical Insulation IEEE Transactions on,2012,19(3):910-916.

[5]李化,程昌奎,陈娇,等.基于EMD的GIS典型局部放电超高频信号的分形特征提取方法[J].高压电器,2014(6):104-110.

[6]杜国山.多功能动态精度实验系统的误差溯源[D].合肥工业大学,2012.

[7]许桢英.动态测量系统误差溯源与精度损失诊断的理论与方法研究[D].合肥工业大学,2004.

[8]蒋敏兰.测量系统精度损失溯源与预测模型研究[D].合肥工业大学,2007.

[9]Huang N E,Shen Z,Long S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis.[J].Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences,1998,454(1971):903-995.

[10]郝刚.改进的EMD在齿轮箱故障诊断中的研究与验证[D].中北大学,2013.

[11]李营,吕兆承.基于EEMD算法的癫痫脑电信号识别[J].重庆工商大学学报(自然科学版),2014(5):90-94.