一种变步长扰动观察法的光伏最大功率跟踪技术的研究
2017-07-07,
,
(三江学院机械与电气工程学院,江苏 南京 210012)
1 引言
在当今世界能源危机以及各国大力倡导新能源开发的大背景下,太阳能的利用越来越受到重视。而光伏发电就是太阳能利用的重要形式,并且随着研究的不断深入和技术的不断提高,光伏发电将成为最有潜力的发电技术之一,这一观点已成为全世界的共识。光伏发电是利用光伏电池接将太阳能转换为电能。与常规发电技术(水力发电、火力发电等)和其他绿色发电技术(风力发电、地热发电等)相比较,光伏发电有以下优势[1]:
(1)太阳能取之不尽,用之不竭,照射到地球上的太阳能比人类生产生活实际消耗大6000倍;且光伏发电安全可靠,能避免能源危机以及煤、石油等燃料市场不稳定因素的冲击。
(2)任何地方都有太阳能,因此,太阳能不像煤炭、石油等能源一样需要运输,更不会被任何人、任何国家和地区所垄断,运行成本较低。
(3)发电过程中不产生工业三废,绿色、低碳、环保。

图1 光伏发电系统分类
对于光伏阵列来说,其输出功率会受到外界环境(光照度、温度等)的影响,且光伏阵列的输出电压不同时输出功率也将随之改变,但系统只有在最大功率点运行时才能充分利用太阳能,因此,需要对光伏阵列进行最大功率点跟踪(Maximum Power Point Tracking,MPPT),调整光伏阵列的工作点以使光伏阵列以最大功率输出。所谓MPPT技术就是以人为的方法控制光伏阵列在最大功率点输出运行的技术手段。扰动观察法是一种人为的改变光伏阵列的工作点、根据对比改变前后光伏阵列的输出功率的变化来确定最大功率跟踪方向的一种自寻优方法。该方法在外部环境发生剧烈变化时,将出现误判现象。在光照度变化不是持续且剧烈的情况下,扰动观察法能够进行自我修正,找到正确的功率跟踪方向,实现最大功率点的跟踪。
本文将详细分析基于扰动观察法的改进方法。其中利用最多的是变步长的思想,即在远离最大功率点的区域使用较大的步长工作,可以提高跟踪速度;在靠近最大功率点的区域使用较小的步长工作,可以提高跟踪精度。变步长的方法不仅可以避免光伏阵列长时间工作在非MPP区域,又可以减少能量损失。
2 光伏电池模型分析
目前,光伏发电系统广泛使用硅光伏电池作为其光电转换器件,该光伏电池相当于一个大的二极管,其等效电路如图2所示。
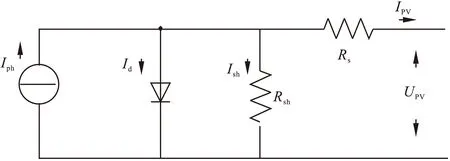
图2 光伏电池板的等效电路图
图中,Iph为光伏电池中由光能激发的电流,它取决于光照度、温度等因素;Id为二极管电流;Rsh为旁漏电阻,是由电池不清洁或电池内部缺陷造成的;Rs为串联电阻;IPV为光伏电池的输出电流,UPV为输出电压。由图2可知输出电流IPV可表述为:
(1)
一般来说,光伏电池的串联等效电阻Rs很小,而并联等效电阻Rsh很大。由于Rsh一般为数千欧姆且并联在电路中,故在进行理想电路计算时可作开路处理,则理想的光伏电池特性为:
(2)
输出电压UPV可写成表达式:
(3)
式(1)~(3)中的参数说明见表1。

表1 光伏电池板的等效电路参数表
从式(2)和(3)可以看出光照度和环境温度对光伏电池板的输出特性有非常直接的影响。在Matlab仿真平台上搭建光伏组件模型,仿真分析不同温度和光照情况下光伏组件的输出特性和功率特性,得到图3和图4所示的一系列曲线。
通过数据抓取,共采集超过5157万条数据,收集海淀区六大战略性新兴产业的7852个行业岗位,岗位覆盖38个细分行业,10681家海淀区六大战略性新兴产业企业。
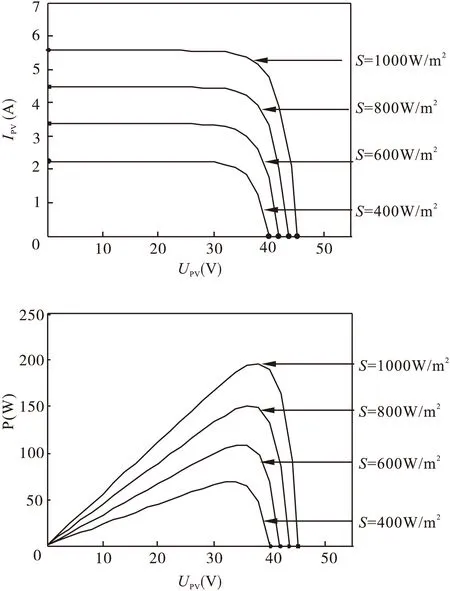
图3 温度T=25℃条件下,改变光照强度时I-U、P-U特性曲线对比图
综上所述,光伏电池的输出功率在不同光照强度和环境温度条件下会发生较大变化,且可以看出光伏电池既不是恒压源,也不是恒流源,而是一个非线性直流电源。
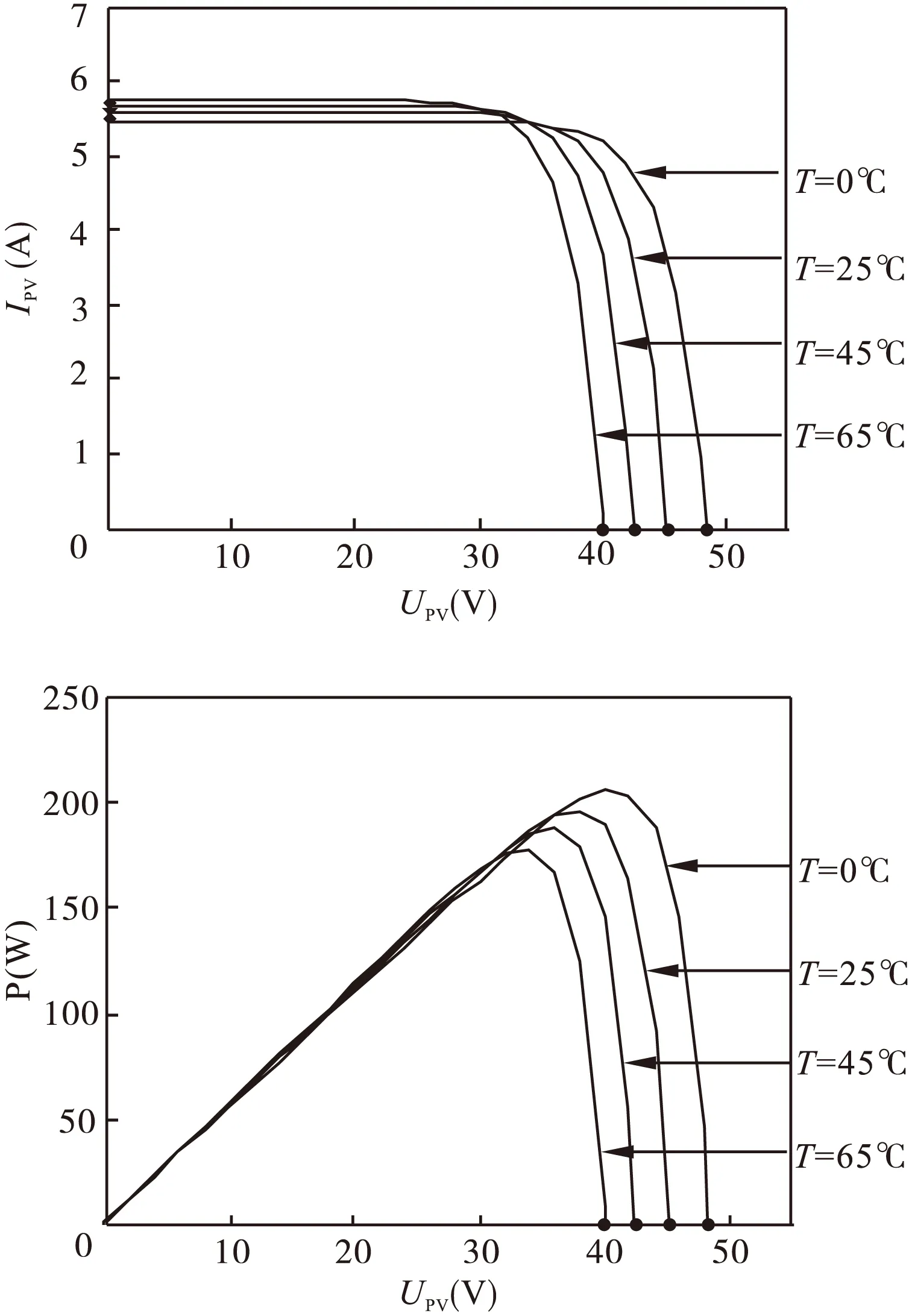
图4 光照强度S=10000W/m2条件下,改变温度时I-U、P-U特性曲线对比图
3 变步长扰动观察法
扰动观察法(Perturbation and Observation method,P&O)是实现MPPT最常用的自寻优类方法,属于自寻优类算法之一。扰动观察法因其原理简单易懂、易于实现、测量的参数较少等诸多方面的优点而被广泛应用。在光照强度变化缓慢的情况下,该方法具有较好的跟踪效果。其基本思想是:首先扰动光伏电池的输出电压(或电流),然后观察光伏电池输出功率的变化[3],若输出功率增大,则可保持扰动方向不变;若输出功率减小,则改变扰动方向,最终使光伏电池工作在MPP。扰动观察法的具体工作流程图如图5所示。
传统的扰动观察法使用的是固定步长值进行扰动以此跟踪MPP,使用较大的步长值可以提高系统的跟踪速度,却增大了振荡幅度而使精度下降;使用较小的步长值可以确保系统的精度,却使速度减缓了,不管是哪种情况最终都将造成系统的能量损耗。为此,提出了变步长的思路。以基于Boost电路的扰动观察法进行说明,如图6所示。
Ta为扰动周期,扰动变量取为占空比D[2]。当占空比D受到扰动时,ΔD表示占空比每次扰动改变的值:

图5 扰动观察法的流程图
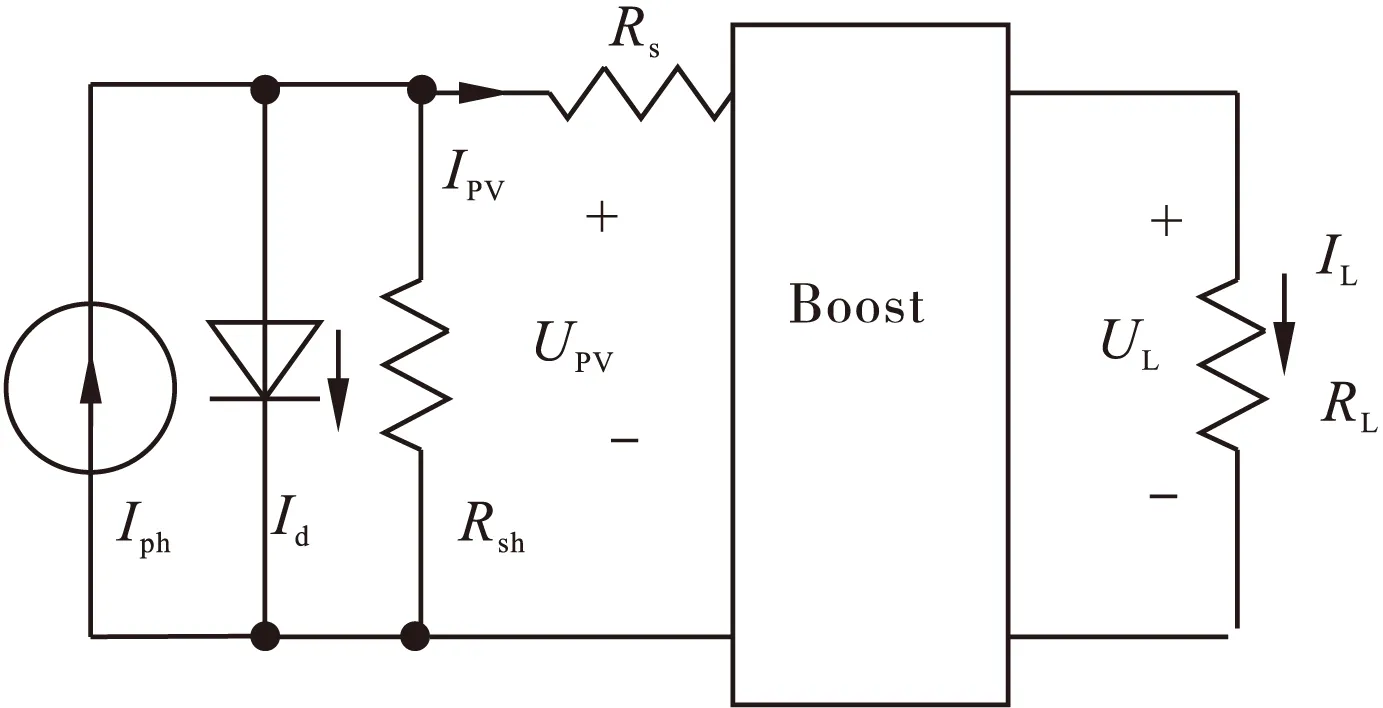
图6 基于Boost电路的光伏电池最大功率跟踪原理图
D((k+1)Ta)=D(kTa)±ΔD
=D(kTa)+{D(kTa)-D[(k-1)Ta]}sign{P[(k+1)Ta]-P(kTa)}
(4)
给占空比一个ΔD的扰动时,经线性化处理后得输出电压响应和输出功率响应:
(5)
(6)


若光照和温度不发生剧变时,式中ΔUd和ΔId表示由占空比扰动引起电压电流变化值,文献[2]中推导出由占空比变化引起的功率变化ΔPd为:
(7)
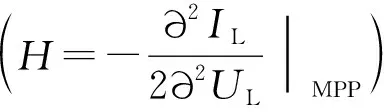
外界环境变化引起的电压变化ΔUd与工作在最大功率点时的输出电压UMPP相比可以忽略,可得由光照变化引起的功率变化ΔPs为:
ΔPs=UMPPΔIs+ΔUdΔIs≈UMPPΔIs=UMPPKΔS
(8)
ΔIs为光伏电池的电流变化值,ΔS为光照度变化值,k为一个材料相关常数,通常k=6.895×10-3A·m2/W。不因外界环境变化而失败的条件是|ΔPd|>|ΔPs|,即
(9)
所以扰动步长ΔD需满足以下约束条件:
(10)
通常ΔS=50W/(m2s),计算可得ΔDmin≈0.001。
4 仿真验证
本文实验正在进行中,此处给出仿真验证。为验证本文所提方法的可行性和有效性,利用MATLAB中的Simulink工具搭建了基于Boost电路的光伏阵列控制电路,如图7所示。将本文所提方法用MATLAB中S-Function进行程序化实现,Boost输出负载接入39Ω电阻,采样时间1e-3s,光照强度为1000W/m2。
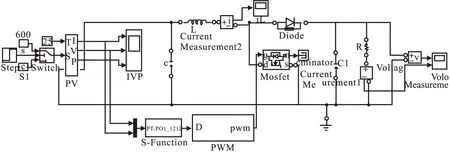
图7 Matlab仿真系统图
对比图8和图9发现当采用大扰动步长时系统的跟踪时间短,但较大的扰动步长也带来了扰动振荡损耗。图10为改进的变步长扰动观察法,该算法的判断原则是当输出功率变化大于2W时选用大步长0.008,否则选用小步长0.004,稳定后振荡幅度较小,跟踪精度明显提高,跟踪时间较快。所以在实际的应用中,应该综合考虑系统的响应能力以及跟踪精度来选择合适的扰动步长,以使系统的综合性能更好。
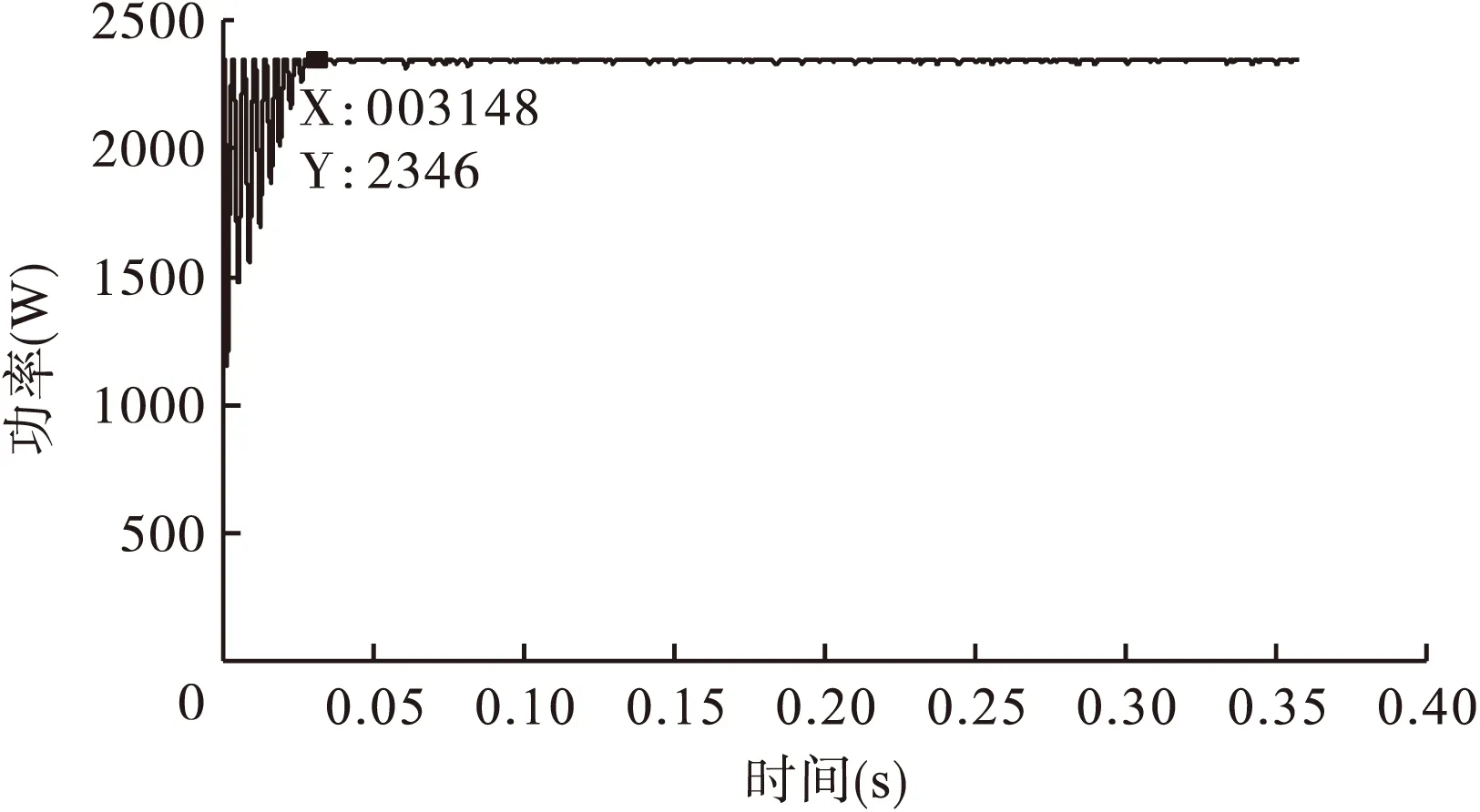
图8 固定步长扰动观察法,扰动步长为0.004时光伏电池输出功率波形
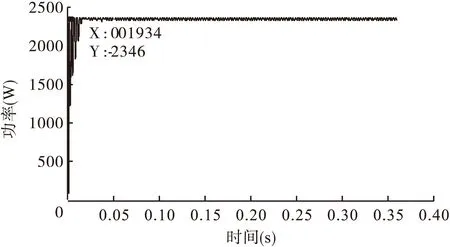
图9 固定步长扰动观察法,扰动步长为0.008时光伏电池输出功率波形

图10 变步长扰动观察法光伏电池输出功率波形
5 结论
本文提出了一种变步长扰动观察法,该控制方法运算简单、跟踪精度明显提高,跟踪速度较快、便于数字化实现。仿真结果验证了该变步长扰动观察法实现最大功率跟踪的可行性和有效性。
[1] 杜琳.基于输出参数的光伏系统最大功率点跟踪控制的研究与实现[D].北京交通大学,2007.
[2] Nicola Femia,Giovanni Petrone,Giovanni Spagnuolo.Optimization of Perturb and Obse-rve Maximum Power Point Tracking Method.IEEE TRANSACTIONS ON POWER ELECTRONICS,2005,20:963-973.
[3] 张兴,曹仁贤,等.太阳能光伏并网发电及其逆变控制[M].机械工业出版社,2010.
[4] 周德佳,赵争鸣,吴理博,等.基于仿真模型的太阳能光伏电池阵列特性的分析[J].清华大学学报(自然科学版),2007,7:19-22,+27.
[5] 赵为.太阳能光伏并网发电系统的研究[M].合肥,合肥工业大学电气与自动化工程学院,2003.
[6] 江小涛.硅太阳电池数学模型[J].武汉科技学院学报,2005,18(8):5-8.
[7] 苏建徽.硅太阳电池工程用数学模型[J].太阳能学报,2001,8(4):409-412.
[8] 赵为.基于DSP芯片的多功能光伏并网发电系统.[D],合肥,合肥工业大学,1999.
[9] Femia N,Petrone G,Spagnuolo G,et al.Optimizing sampling rate of P&O MPPT technique[C]//Power Electronics Specialists Conference,2004.PESC 04.2004 IEEE 35th Annual.IEEE,2004,3:1945-1949.
[10] Xiao W,Dunford W G.A modified adaptive hill climbing MPPT method for photovoltaic power systems[C]//Power Electronics Specialists Conference,2004.PESC 04.2004 IEEE 35th Annual.IEEE,2004,3:1957-1963.
[11] MAO M,YU S,SU J.Versatile Matlab Simulation Model for Photovoltaic Array with MPPT Function [J].Acta Simulata Systematica Sinica,2005,5:058.
