永磁同步电机AEKF无磁链直接转矩控制
2017-07-07,
,
(福州大学 电气工程与自动化学院,福建 福州 350100)
1 引言
在永磁同步电动机(PMSM)的控制方式中,直接转矩控制(DTC)因其具有转矩响应速度快、控制与计算简单等特点被广泛使用,传统的直接转矩控制是在定子两相静止坐标系下观测磁链,计算转矩,并对两者同时进行滞环控制[1-3]。但考虑到控制目的仅仅是为提高电机电磁转矩响应的快速性,没有理由非要将定子磁链幅值控制在恒定值,因此可以简化传统DTC控制,引入无磁链DTC控制[4],这种方法在定子磁链还未超过磁链限幅值时单独控制电磁转矩,由于控制方式更加直接,因此提高了电磁转矩的响应速度和精度,同时使转矩脉动有所降低。
此外,因为直接转矩控制无需旋转坐标变换,对转子位置信息要求不高,所以易于实现无传感器控制。目前使用较多的方法有:模型参考自适应法[5]、滑模变结构法[6]、扩展卡尔曼滤波法(EKF)[7-10]等。由于EKF思路简单,应用范围广泛且应用效果尚可,因此本文采用扩展卡尔曼滤波法,并将其引入永磁同步电机无磁链DTC控制中。但是,由于该方法的滤波效果受噪声影响很大,错误的噪声协方差矩阵会使系统发散,而该矩阵的选取目前往往依靠试凑得到,所以本文在扩展卡尔曼滤波的基础上引入噪声自适应算法,目前较为常用的自适应扩展卡尔曼滤波器有:相关法自适应滤波[11]、基于极大似然准则的自适应滤波[12]、Sage-Husa自适应滤波[13-14]、协方差匹配自适应滤波[15]等。本文将协方差匹配自适应滤波与Sage-Husa自适应滤波相结合,使系统噪声和量测噪声可以自适应调节,提高系统的收敛性能以及观测精度。
2 永磁同步电机数学模型
本文所有研究都是针对正弦波隐极式永磁同步电动机,且电机定子绕组为星形连接,这类永磁同步电机应用最为广泛,隐极式永磁同步电机交直轴电感相同,无磁阻转矩分量,计算较为方便。
xy坐标系下永磁同步电动机数学模型表示为:
(1)
(2)
由于定子磁链定向于x轴,所以φy=0,于是由(1)、(2)可得转矩方程为:
(3)
φx、φy、ux、uy、ix、iy分别为定子磁链、电压和电流x、y轴分量;φf为永磁体磁链;|φs|为定子磁链幅值;δ为定转子磁链夹角;Rs、Ls分别表示定子电阻和电感;p为电机极对数;ωr为转子磁链电角速度。
3 无磁链DTC原理概述
传统PMSM DTC理论是根据式(3),保持定子磁链幅值恒定,控制转矩角δ的变化实现对电磁转矩的实时控制。无磁链DTC不再保持定子磁链幅值恒定,只把转矩当做主要控制量,实现更快速更准确的转矩响应。
式(3)两边对δ求导,可得:
(4)
当开关频率很高时,转矩和转矩角变化很小,这时(4)可以化简为:
(5)
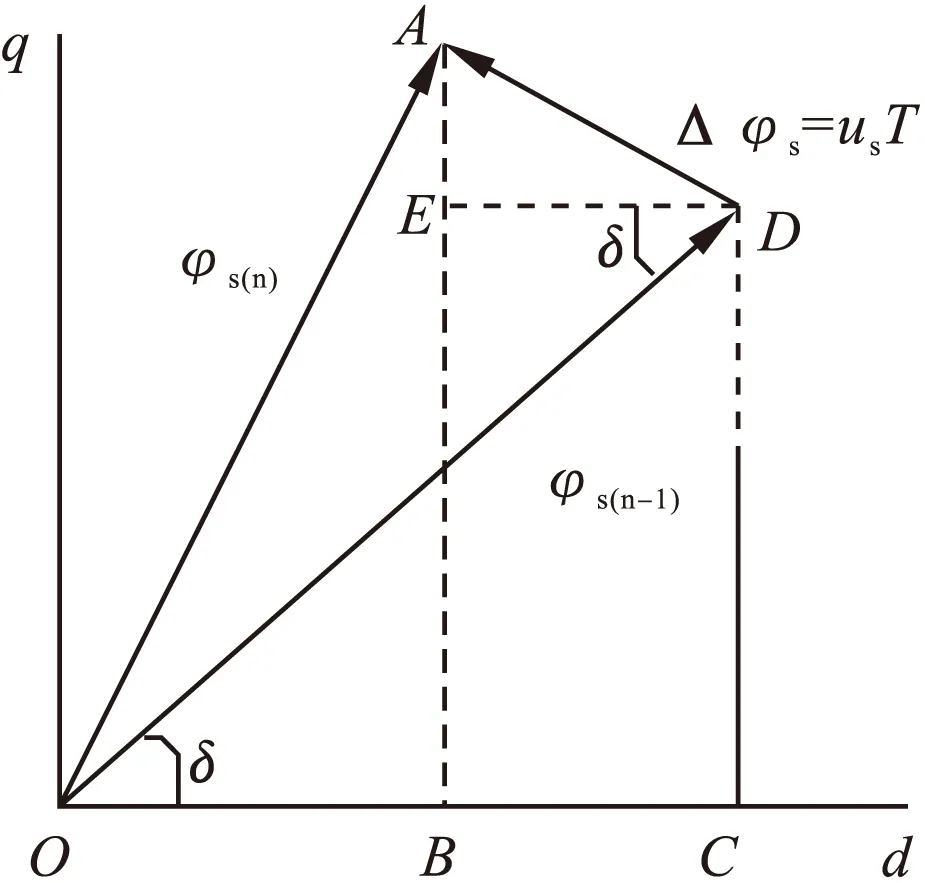
图1 定子磁链与电压矢量关系图
结合图1,因为在一个开关周期内磁链变化很小,可以认为DA与OD垂直,因此得到转矩角变化量:
(6)
将上式带入(5),可进一步化简为:
(7)
如图1所示,做DE垂直于AB,由于DA垂直于OD,则∠BAD=∠ODE=δ,AE可以视为Δφs在交轴上的分量,当忽略定子电阻时,在一个开关周期内定子磁链交轴分量与电压矢量交轴分量的关系可表示为:
φq=uqT
(8)
结合式(5)电磁转矩可表示为:
(9)
根据式(9)可以看出,为了更加突出直接转矩直接控制转矩这一特点,可以只控制电压矢量的交轴分量,不需要考虑磁链,该方法控制简单快捷,理论上可以提升转矩的动态响应性能。
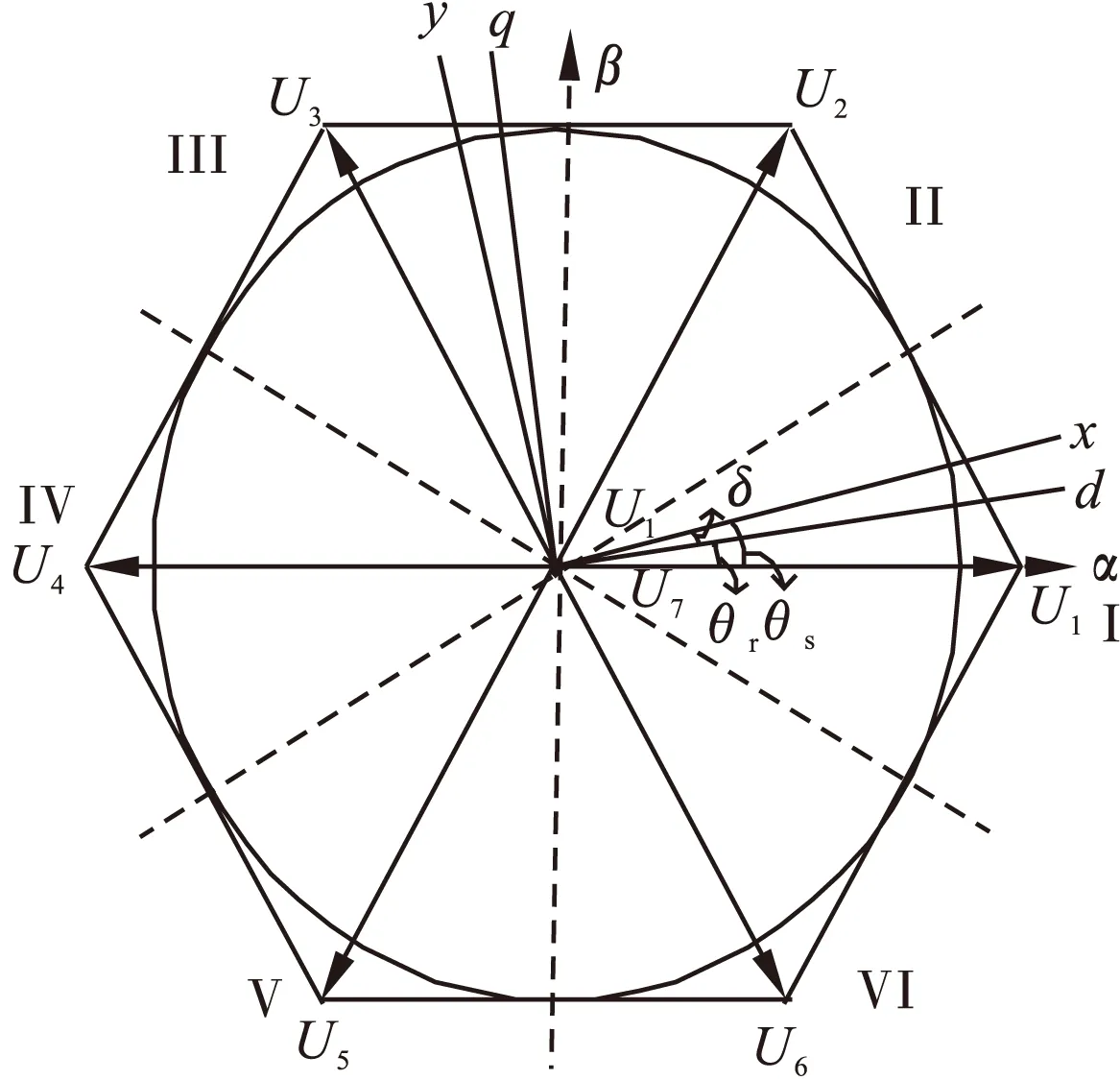
图2 空间电压矢量与各坐标系关系图
由图2可以得到六个非零电压矢量交轴分量表达式为:
(10)
如图2所示,在2π周期内可以分为6个扇区,每个扇区选择对电磁转矩影响最大的一个电压矢量,拿一扇区(0°~60°)举例来说,由式10可知,当需要增大转矩时,u3q对电磁转矩影响最大;当需要减小转矩时,采用u6q可以最快的降低电磁转矩;为了减小转矩脉动,在一定范围内将零矢量作用于电机。各扇区电压矢量的选择如下表所示,当τ为1时表示需要增加电磁转矩,当τ为0时,表示采用零矢量保持电磁转矩,当τ为-1时表示需要减小电磁转矩。
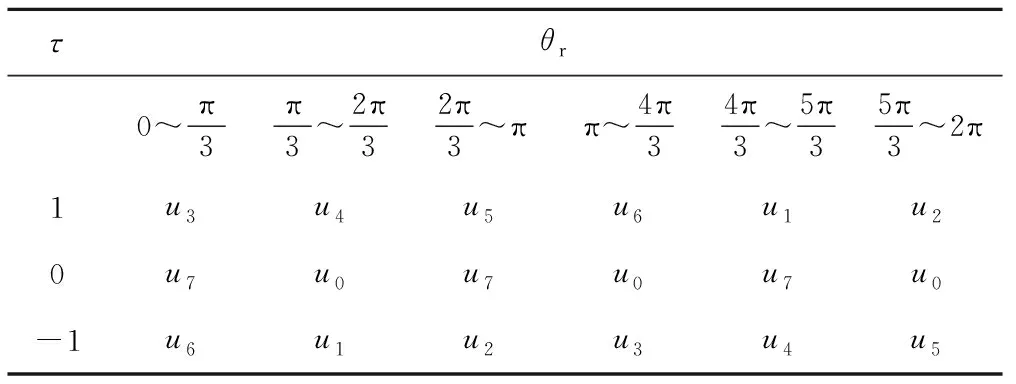
表1 无磁链条件下电压矢量选择表
上述控制方法只考虑了定子磁链的交轴分量,但电压矢量作用后还会使磁链直轴分量产生变化,一定情况下定子磁链幅值可能会超过额定值,导致定子绕组磁饱和,严重时可使电机停转。因此需要在磁链超出额定值时对其限幅。XY坐标系以定子磁链定向,因此在忽略定子电阻的情况下,空间电压矢量的X轴分量可以直接决定定子磁链幅值,此外Y轴分量决定了电机转矩角的变化,可以控制电磁转矩的增减。
由图2可以得到非零电压矢量的XY轴分量分别为:
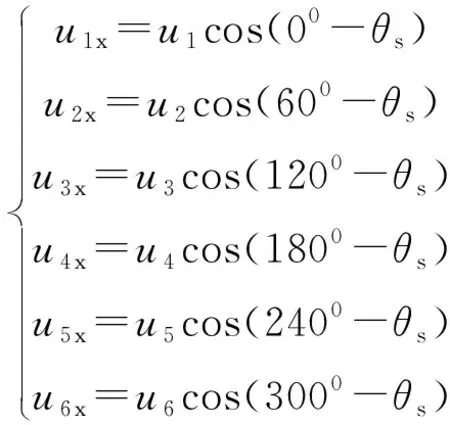
(11)
(12)
同样可将2π周期分为6个扇区,拿一扇区(-30°~30°)举例,根据式(11)、(12)此区间内可以减小磁链幅值的电压矢量有u3、u4、u5三个矢量,如果此时需要增加电磁转矩只能选择u3;反之需减小电磁转矩时只能选择u5;假如需要保持电磁转矩需要选择在此扇区中正负变化量相等的电压矢量,即u4。各扇区电压矢量选择如表2所示。
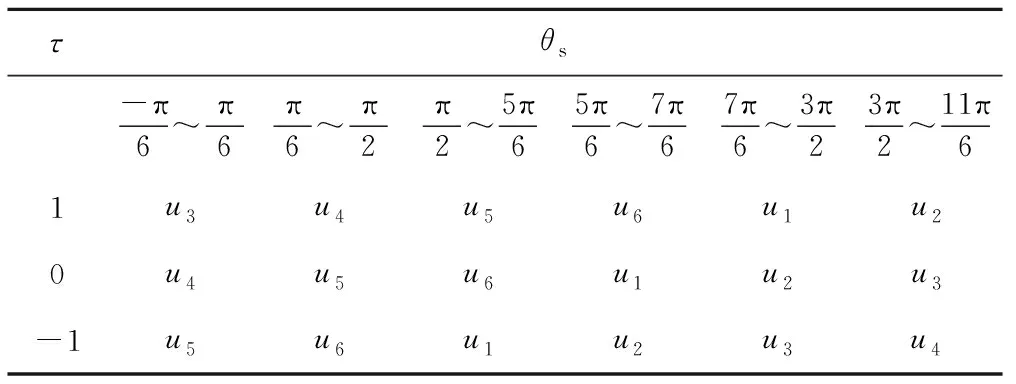
表2 磁链限幅条件下电压矢量选择表
综上,在磁链未达到额定磁链时参照表1进行控制,当磁链超过额定限幅,参照表2进行控制,以上就构成了无磁链直接转矩控制的理论基础。
4 AEKF观测器设计
4.1 EKF原理概述
EKF滤波步骤可分为以下两步:
(1)预测阶段。计算状态预测值x和预测误差方差阵P,即:
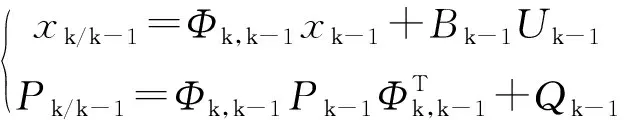
(13)
(2)更新阶段。计算EKF增益矩阵K,进行状态预测值和预测误差方差阵的更新,即:
增益矩阵:
(14)
状态预测值和预测误差方差阵更新:
(15)
Φk,k-1≈
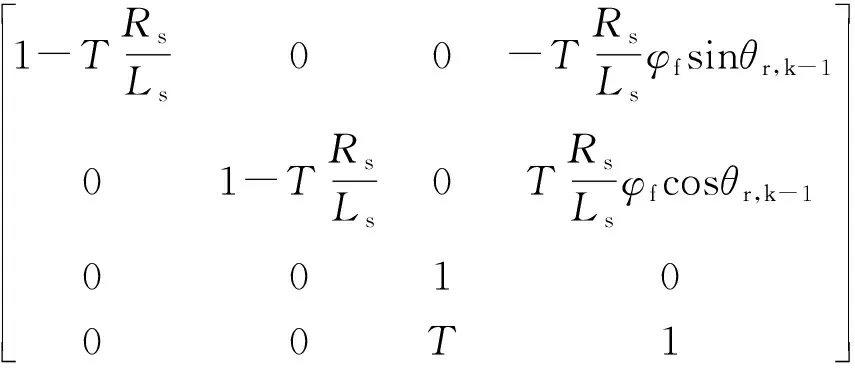
(16)
(17)
(18)
将以上矩阵代入式(13)~(15)经过数次迭代后可以估计出状态变量真实值,用于PMSM DTC中。
4.1 系统噪声估计器
根据理论分析以及实验探究,扩展卡尔曼滤波必须在状态模型和噪声统计特性准确描述的情况下才可以达到预期效果。系统噪声协方差矩阵与量测噪声协方差矩阵的选取直接影响整个系统的收敛效果,虽然在电机模型下噪声矩阵是简单白噪声,但是目前选取噪声协方差矩阵主要靠试凑得到。因此本文提出一种自适应卡尔曼滤波理论,可以准确的得到随系统参数变化的噪声协方差矩阵,保证系统快速收敛。
本文将Sage-Husa自适应扩展卡尔曼滤波与协方差匹配法相结合,Sage-Husa自适应扩展卡尔曼滤波用来估计系统噪声,协方差匹配法用来估计量测噪声。该方法既避免了Sage-Husa自适应滤波法计算复杂的缺点,另一方面已有文献证明,系统噪声与量测噪声不能被Sage-Husa自适应滤波法同时观测,所以该方法保证两类噪声都被观测的前提下仍然保证了系统鲁棒性。
Sage-Husa自适应扩展卡尔曼滤波时变系统噪声估计器表达式如下:
(19)
(20)
根据卡尔曼迭代公式可知滤波新息为:
(21)
式(19)中b表示遗忘因子,其取值范围为0.95~0.995,本文实验中取0.95。由于最后一项数值很小,为方便收敛,将(20)化简为系统噪声协方差矩阵Qk的有偏估计:
(22)
此时将Qk参与EKF迭代过程,实现自适应滤波。
4.2 量测噪声估计器
将Yk=Hkxk+vk代入(21),得:
(23)
由(23)式可得到新息的理论协方差为:
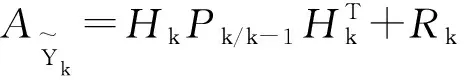
(24)
实际的新息协方差可表示为:
(25)
其中N为滑动窗口大小。
将协方差实际值等效为理论值,可以得到量测噪声协方差矩阵为:
(26)
该方法的观测性能受滑动窗口大小的影响,较小的滑动窗口计算量小,但观测结果波动性大,较大的滑动窗口计算量过大对硬件性能要求苛刻,本文实验中选取的滑动窗口为100。因此,在前100个控制周期内,可以先固定量测噪声协方差矩阵,利用Sage-Husa自适应扩展卡尔曼滤波得到系统噪声协方差矩阵的值,随后进行量测噪声的估计,使得在每个控制周期内都有至少一个噪声协方差矩阵在修正,提高EKF观测性能。
5 仿真与实验验证
5.1 仿真分析
为了验证以上理论的正确性,用Matlab/Simulink进行仿真分析,其中AEKF算法用S-function来实现,电机主要参数如表1所示。

表1 永磁同步电机主要参数
仿真中转速给定为600r/min,负载转矩为空载启动,0.2s后突加负载至4N*m,分别采用传统零矢量DTC、无磁链DTC进行仿真分析。两者的磁链、转矩与转速波形如图3~6所示。

图3 传统零矢量DTC定子磁链波形
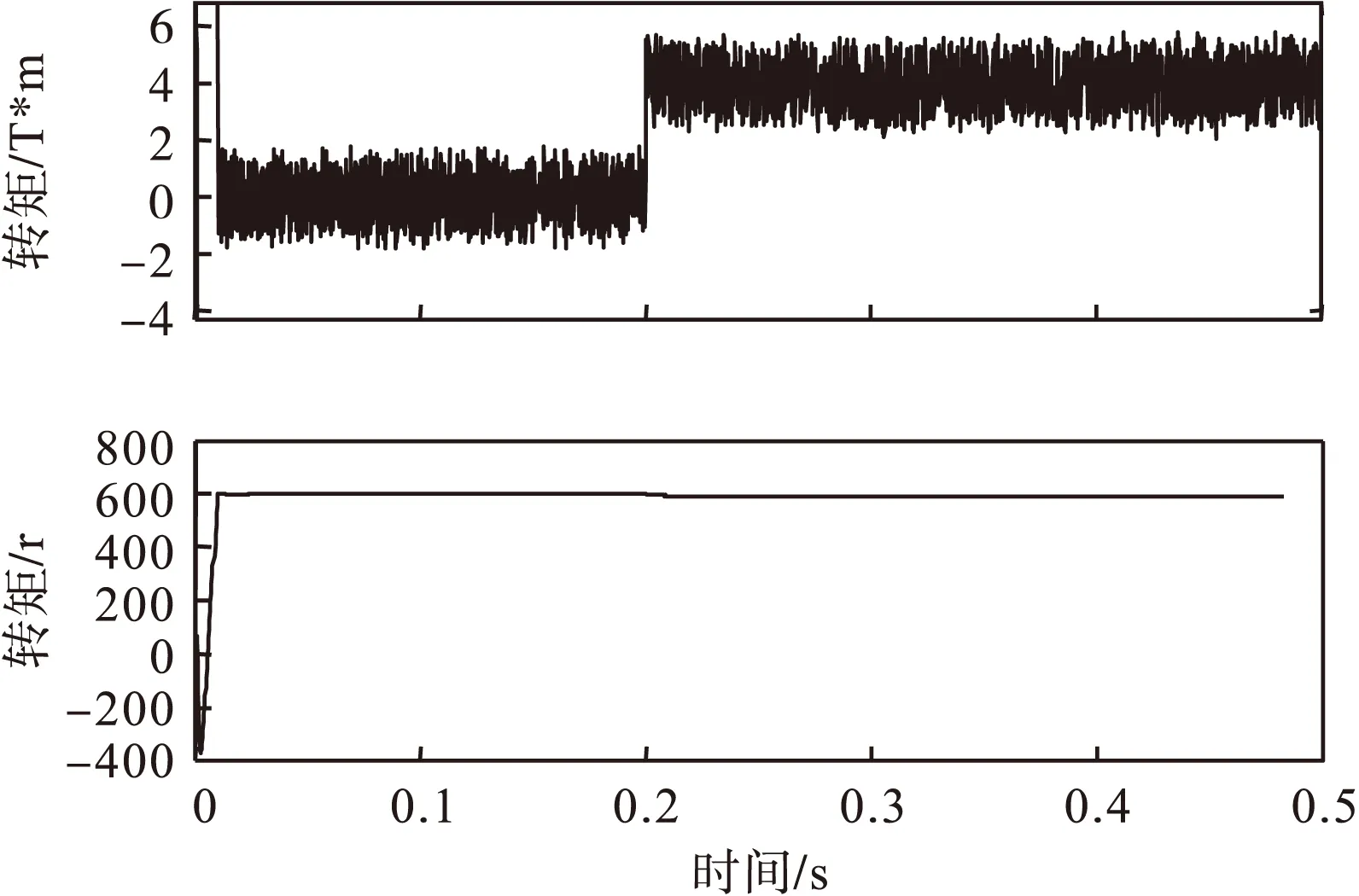
图4 传统零矢量DTC转矩和转速波形

图5 无磁链DTC定子磁链波形
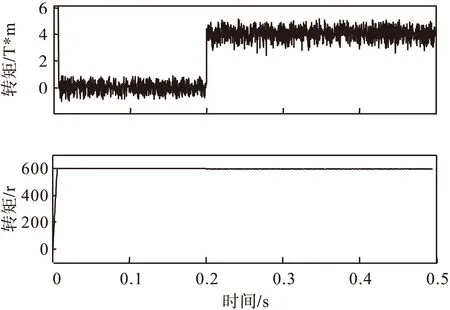
图6 无磁链DTC转矩和转速波形
根据仿真波形可以看出,无磁链DTC定子磁链波形并非标准的圆形,在空载时定子磁链大部分时间小于磁链限幅,增大转矩至4N*m时,磁链近似于圆形磁链但始终没有超出限幅,此外由于在无磁链DTC更加直接的控制电磁转矩,其转矩脉动更小,响应速度上无磁链DTC更快速。
在无磁链DTC控制的基础上加入AEKF算法,在试验了较多的噪声协方差矩阵后,发现AEKF在许多EKF无法收敛的噪声矩阵下都能持续收敛,且收敛速度明显优于EKF算法,参数矩阵选择如下;将AEKF观测器参与闭环,磁链、转矩、转速以及转子位置角仿真波形如图7~9所示。


图7 AEKF无磁链DTC定子磁链波形
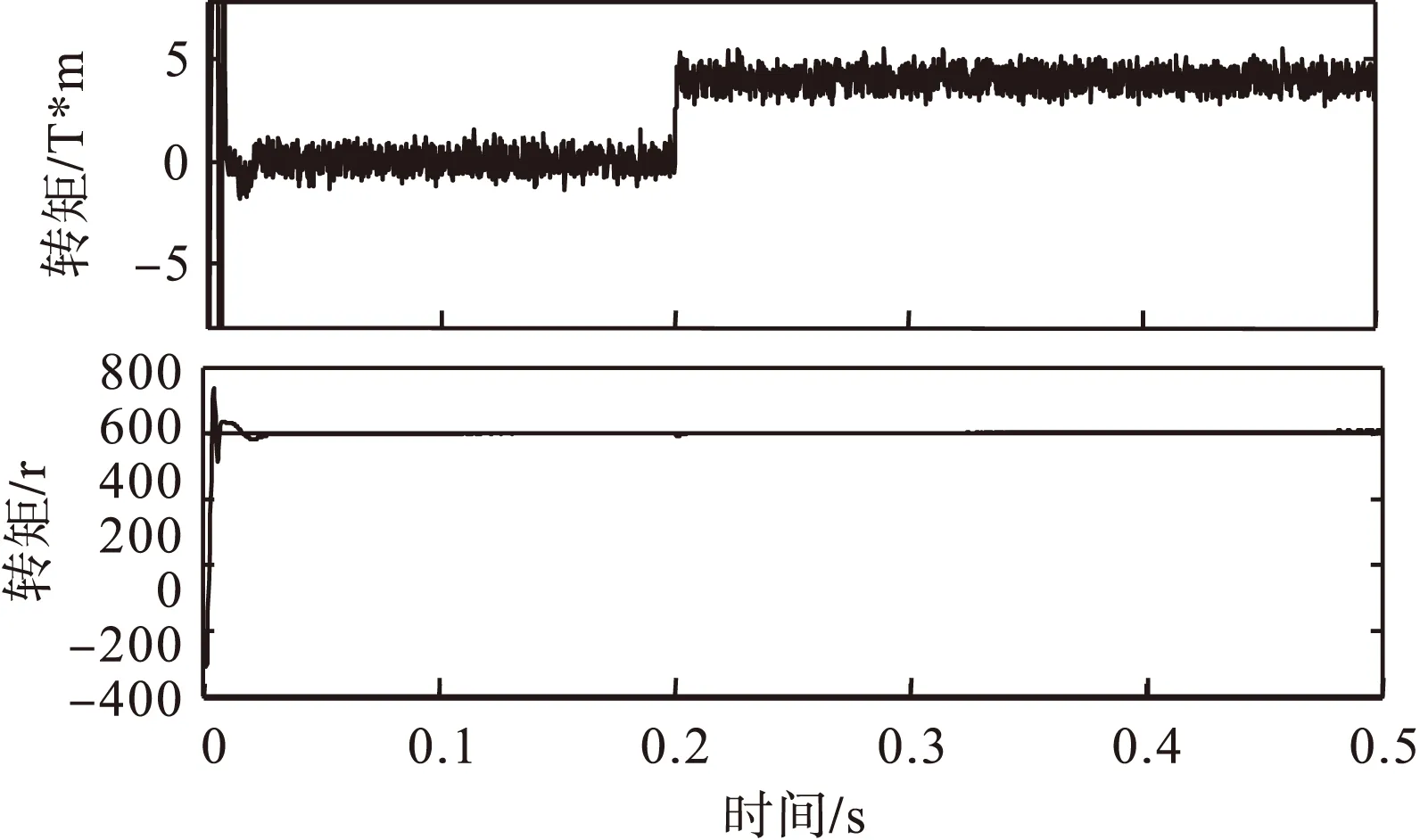
图8 AEKF无磁链DTC转矩和转速波形

图9 实际位置角与AEKF估计位置角对比波形
由仿真波形可以看出,AEKF无磁链DTC控制不仅保留了其转矩响应速度快的特点,而且磁链、转矩脉动有所减小。可以看到,AEKF观测器下转子位置角波形略滞后于实际位置角,但误差很小,因此仍能保证电机稳定运行。
5.2 实验分析
本文采用TI 公司DSP TMS320F2812作为控制核心,功率变换装置采用富士公司7MBP50RA120智能功率模块,永磁同步电机为隐极式正弦波伺服电机,电机主要参数与表1相同,所带负载为一个三相同步测功机。分别对无磁链DTC、EKF无磁链DTC及AEKF无磁链DTC进行实验分析,给定转速为600r/min,空载启动待转速稳定后,突加2.7N*m负载转矩。图10~17为CCS3.3程序示波器观测下的无磁链DTC、EKF无磁链DTC和AEKF无磁链DTC转速转矩、定子磁链以及位置角波形。
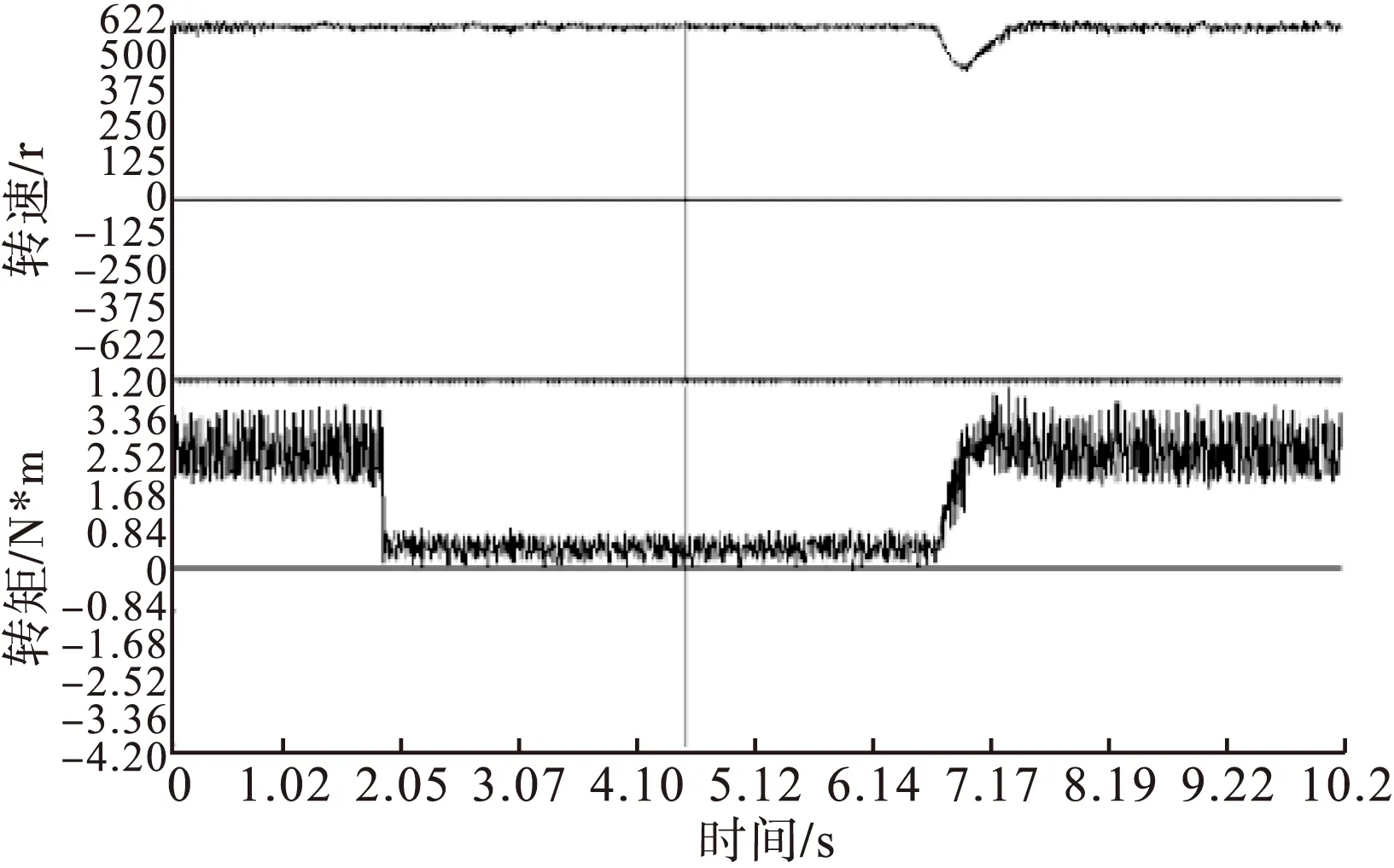
图10 无磁链DTC转速和转矩波形
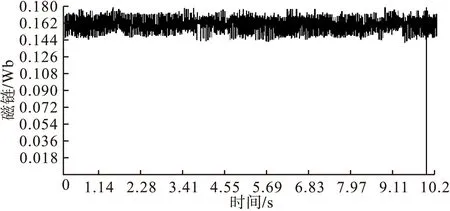
图11 无磁链DTC定子磁链波形
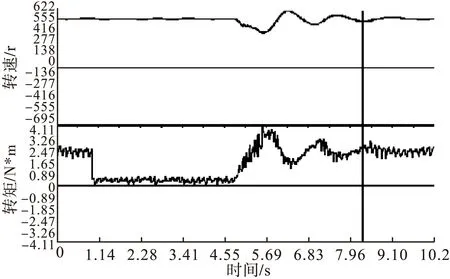
图12 EKF无磁链DTC转速和转矩波形
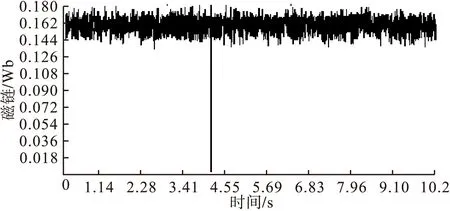
图13 EKF无磁链DTC定子磁链波形
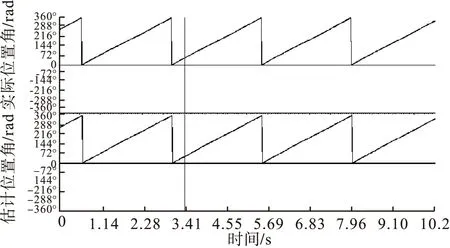
图14 实际位置角与EKF估计位置角对比波形
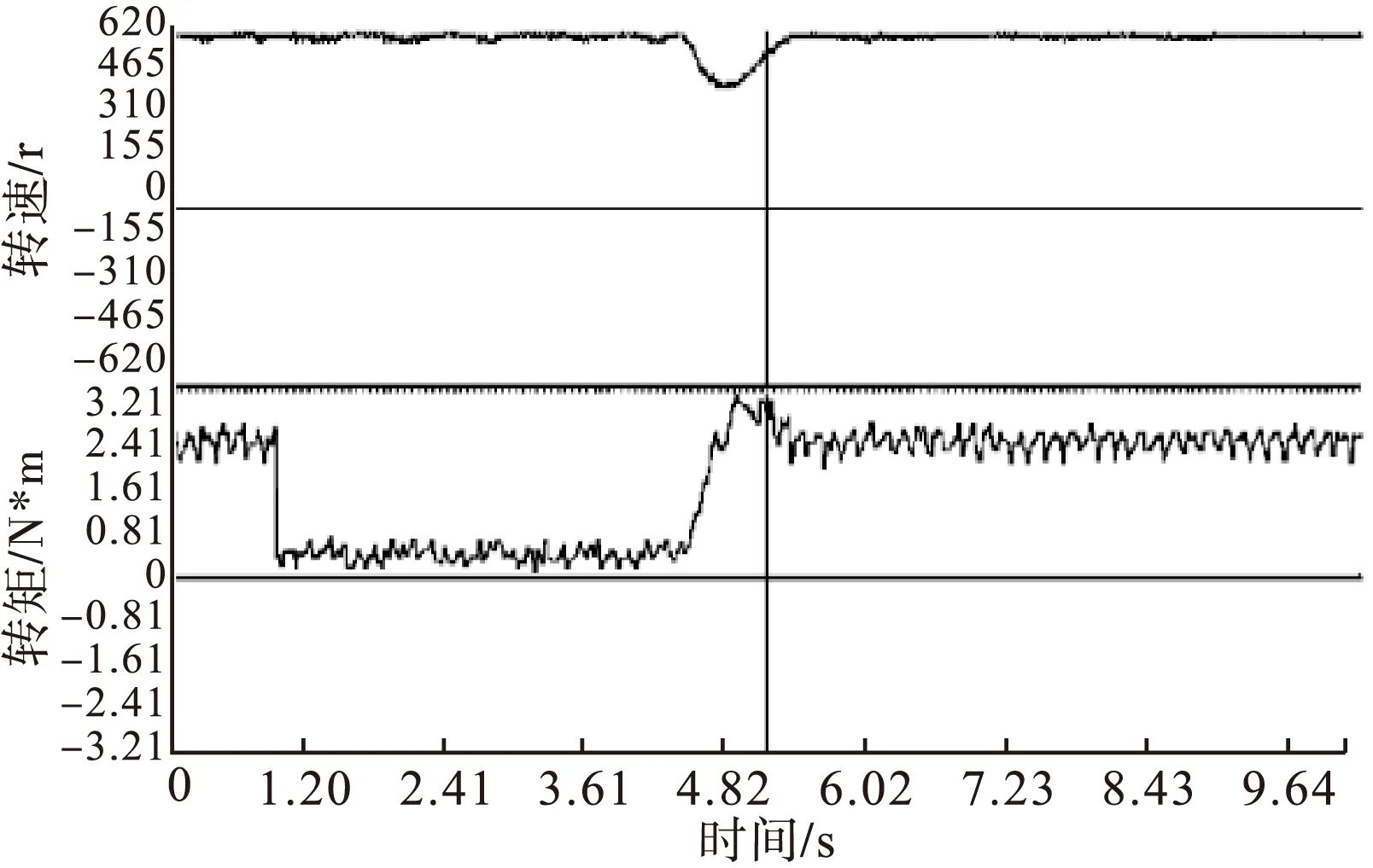
图15 AEKF无磁链DTC转速和转矩波形
根据图12和图15可以看出,EKF和AEKF无磁链DTC对转速转矩脉动都有了明显改善,转矩脉动较无磁链DTC减小了约0.65N*m,但EKF无磁链DTC在突加转矩后收敛速度较慢,突加时刻会产生较大超调,而AEKF无磁链DTC有效的克服了这一点,保证了较快的转矩响应及收敛性,转矩超调也明显减小;对比图11、13、16可以看出加入AEKF观测器的定子磁链脉动更小;位置角波形方面EKF和AEKF观测器都有准确的观测效果。
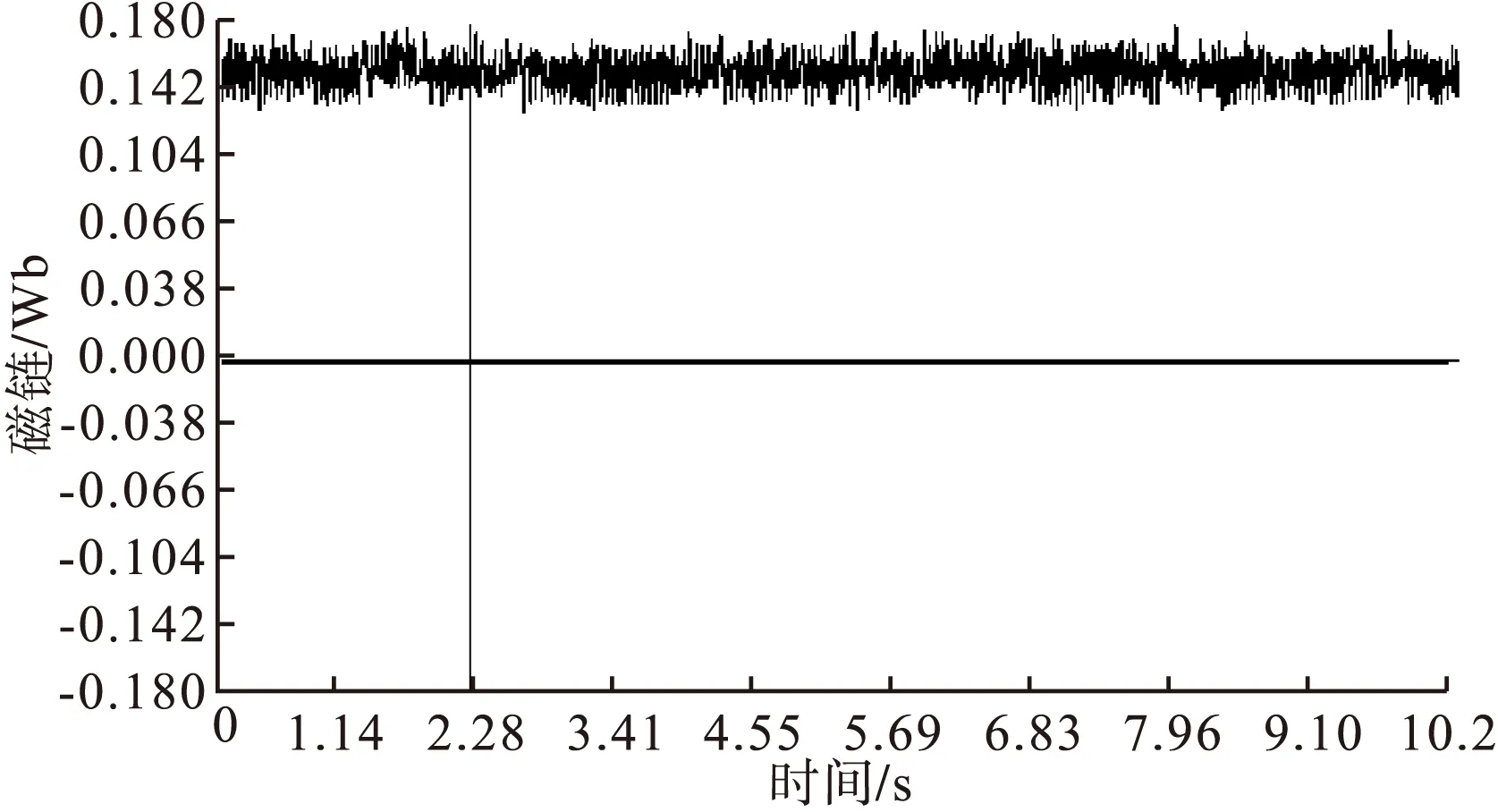
图16 EKF无磁链DTC定子磁链波形
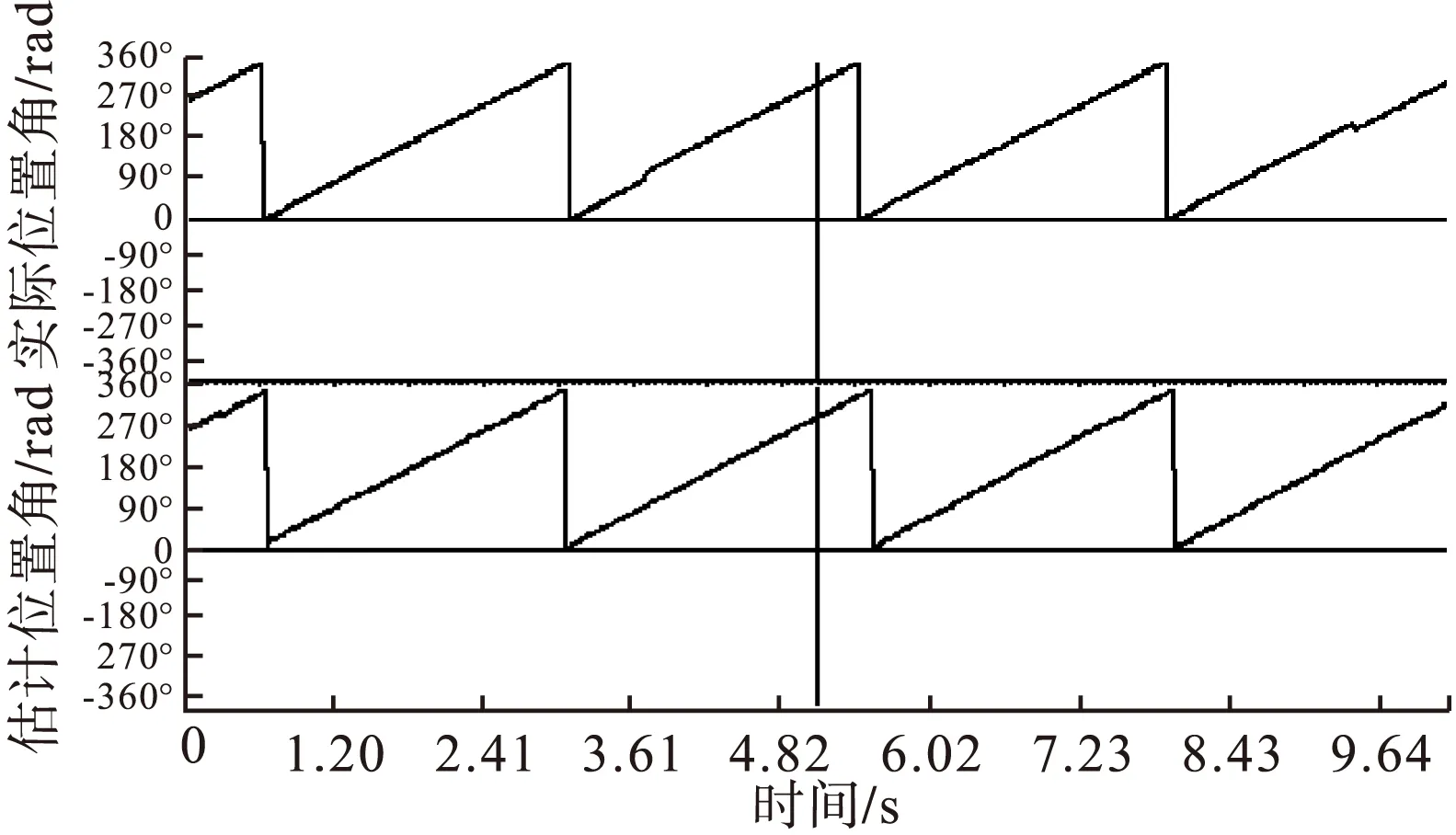
图17 实际位置角与AEKF估计位置角对比波形
6 结论
为了优化传统DTC的控制性能,本文提出了星形连接正弦波永磁同步电动机无磁链DTC控制,该方法在定子磁链到达限幅之前只控制电磁转矩大小,由于控制直接作用于转矩,因此该方法加快了转矩响应速度并减小了转矩脉动。为了进一步优化控制效果,在无磁链DTC的基础上引入EKF无传感器控制,该方法不仅提高了实验研究的经济性而且估计数据接近于真实值,使得转矩脉动有明显下降,但EKF受噪声矩阵影响较大,而噪声矩阵目前又只能通过试凑的方法得到,这大大限制了EKF算法的收敛性,导致在电机负载变化时系统不能快速收敛。所以本文提出一种新型自适应EKF算法,将Sage-Husa法与协方差匹配法相结合,并通过仿真和实验证明AEKF算法有更好的观测效果和更快的收敛速度。
[1] Rahman M F,Zhong L,Haque M DEnamul,et al.A direct torque-controlled interior permanent-magnet synchronous motor drive without a speed sensor[J].IEEE Transactions on Energy Conversion,2003,18(1):17-22.
[2] HU Yuwen,TIAN Chun,YOU Zhiqing,et al.Direct torque control system and sensorless technique of permanent magnet synchronous motor [J].Chinese Journal of Aeronautics,2003,16(2):97-102.
[3] 陈振,刘向东,戴亚平,等.采用预期电压矢量调制的PMSM直接转矩控制[J].电机与控制学报,2009,13(1):43-44.
[4] 胡育文,高瑾,杨建飞,等.永磁同步电动机直接转矩控制系统[M].机械工业出版社,2015:54-55+60.
[5] 佘致廷,肖岸文,孙炜,等.基于MRAS理论的无速度传感器直接转矩控制调速系统[J].电工技术学报,2006,21(4):99-100.
[6] 孙振兴,张兴华.基于滑模观测器的感应电机无速度传感器直接转矩控制[J].电工电能新技术,2012,31(4):30-31.
[7] 刘英培,万健如,沈虹,等.基于EKF PMSM定子磁链和转速观测直接转矩控制[J].电工技术学报,2009,24(12):58-59.
[8] 刘英培,万健如,梁鹏飞.基于扩展卡尔曼滤波器和空间电压矢量调制的永磁同步电机直接转矩控制[J].中国电机工程学报,2009,29(27):70-72.
[9] 陈振,刘向东,靳永强,等.采用扩展卡尔曼滤波磁链观测器的永磁同步电机直接转矩控制[J].中国电机工程学报,2008,28(33):77-81.
[10] 刑岩,王旭,杨丹,等.改进定子磁链估计器及其参数选取[J].电机与控制学报,2016,20(3):32-33.
[11] 计会凤.基于浮动车GPS数据的动态交通预测与诱导模型研究[D].辽宁:辽宁工程技术大学,2009:71-73.
[12] 岳晓奎,袁建平.一种基于极大似然准则的自适应卡尔曼滤波算法[J].西北工业大学学报,2005,23(4):469-472.
[13] 闵伟,周志宇,周振华.改进型Sage-Husa卡尔曼滤波器在电压暂降检测中的应用[J].电网技术,2013,37(1):231-232.
[14] 杨学海,张继业,张晗.基于改进Sage-Husa的自适应无迹卡尔曼滤波的锂离子电池SOC估计[J].电工电能新技术,2016,35(1):32.
[15] 赵琳,等.非线性系统滤波理论[M].国防工业出版社,2012:36-41+193.
