仿蟹机器人横行步态运动稳定性及能耗分析

韩金华, 王海龙,王刚,叶秀芬,王立权

(1.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001； 2.哈尔滨工程大学 机电工程学院，黑龙江省 哈尔滨 150001； 3.哈尔滨工程大学 水下机器人技术重点实验室，黑龙江 哈尔滨 150001)



仿蟹机器人横行步态运动稳定性及能耗分析

韩金华1, 王海龙2,王刚3,叶秀芬1,王立权2

(1.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001； 2.哈尔滨工程大学 机电工程学院，黑龙江省 哈尔滨 150001； 3.哈尔滨工程大学 水下机器人技术重点实验室，黑龙江 哈尔滨 150001)

为提高仿蟹机器人横行步态的运动稳定性、降低系统能耗，本文以规范化能量稳定裕量和能耗比作为步态优劣评价指标，对仿蟹机器人的步序和步态参数进行了规划研究。在动力学分析的基础上，建立了机器人足端脚力的多约束方程，利用伪逆法对机器人各关节力矩进行优化分配，在考虑直流电机的有效功率和热损耗的基础上，构建了仿蟹机器人能耗比数学模型。以多足机器人常采用的等相位步态为例，分析了步行速度、占地系数、步长和机体同侧相邻步行足相位差对系统能耗和稳定性的影响。结果显示：随着机体同侧相邻步行足相对相位的增加，仿蟹机器人的运动效率降低，但稳定性有所改善；在特定的步进速度和步态占地系数下，通过合理选择相对相位能够节省系统能耗20%～30%。

仿蟹机器人；能耗比；规范化能量稳定裕量(NESM)；步态规划；稳定性；步态运动；横行步态

足式机器人相比于轮式、履带式机器人具有较高的运动稳定性和较强的环境适应性，其冗余肢体结构使其能在复杂环境中仍保持稳定状态，即使个别关节出现故障仍然可以完成作业，适合于完成各种非结构环境中的运输任务，因此具有很强的实用价值[1]。然而，对于一个高度自治的足式机器人除了需要承受自身躯干重量，还要携带控制单元、能量储存单元和任务负载等，从而导致了其运动效率极其低下。为使足式机器人真正服务于人类的一个关键要素就是降低系统能耗[2]。近20年来，科研人员提出了多种方法对足式机器人系统能耗进行优化，可大致分为以下五类：1) 高效的机器人躯体结构和腿部机构的设计[3]；2) 采用能量储存单元吸收收集步行过程中耗散能，为下一时刻的动作储存能量[4]；3) 以系统能耗作为评价指标，对摆动相轨迹进行优化[5]；4) 高效的步态规划方法和步态参数的合理选择[6]；5) 适宜的脚力分配方法[7-8]。Yu等对常见的两种不同型腿足结构的机器人的系统能耗进行对比分析，得出哺乳动物型结构比昆虫型能效特性优越[9]。Erden等基于径向基函数神经网络，以能耗最小化为优化指标，对三关节步行足摆动相轨迹进行了优化，并将得到的轨迹与生物腿轨迹进行比较，得出直接模仿生物腿的摆动并不是最高效结论[10]。Roy等设计了软计算专家系统，可用于六足机器人转弯步态的稳定裕量和能耗的预测，但是没有给出如何降低机器人能耗的方法[11]。Gonzalez等讨论了六足机器人步行足在躯体两侧的布置方式对脚力分配和能耗比所造成的影响，得出适当选择中间腿的位置，可使足尖点承受最大地面反力降低15%，可有效降低系统能耗[12]。Maehefka等分析了步态参数(速度、占地系数、步长、落地足位置、机体高度)对多足机器人系统能耗的影响，通过选择一组最佳步态参数组合可以使机器人的能耗降低50%以上[13]。Roy等采用两种不同方法进行足力分配，建立了真实六足机器人的能耗模型，分析了波形步态和转弯步态步态参数对机器人能耗和稳定性的影响，得出直接进行关节扭矩分配较脚力分配更加高效[14-15]。王刚等通过对生物螃蟹行走过程分析，提出了“交错等相位波形步态”，机器人采用该种步态行走具有良好的稳定性和较小的功率波动幅度[16]。

以往开展足式机器人系统能耗和运动稳定性的研究基本都是针对纵向行走步态，而且在建立系统稳定性和能耗模型时，对步行足和机体模型进行了过度简化，得到的结论与真实机器人运动规律并不相符。最为重要的是，以往的研究侧重点都放在研究步态参数对能耗和稳定性的影响，而没有考虑机体同侧相邻步行足之间摆动相位对机器人的系统能耗和稳定性的影响。本文建立了仿蟹机器人能耗比和规范化能量稳定裕量的数学模型，基于该模型探讨了机器人横行步态步态参数和机体同侧相邻步行足相对相位对系统稳定性和能耗的影响，并进行了实验验证。

1 能耗比和规范化能量稳定裕量数学模型

1.1 仿蟹机器人样机

以生物河蟹作为仿生原型，针对河蟹结构更易于横行行走的特点，研制八足仿蟹机器人样机，如图1所示。仿蟹机器人主体采用左右对称式结构，其主要由结构本体、控制系统、八条模块化步行足等组成。控制系统包括定位导航模块、无线遥控模块、液晶显示模块等。每条步行足由基节、股节、胫节、指节、应力传感器及连接架等部分组成，其中胫节和指节彼此不存在相对运动，简化为一体，即将每条步行足分解为三个模块化的传动关节。为满足模块化关节传动系统间隙小、刚度大、输出扭矩高，具有自锁性等要求，每个模块关节都由一个带减速器的电机和蜗轮蜗杆传动机构构成。为了使机器人在横向平动时，各关节的驱动力尽可能地作用在运动方向上，提高机器人的运动效率，降低能耗，在考虑机器人各步行足的布置方式时，以其有效分力最大化为目标，同时兼顾其外形以及布置方式对机器人灵活性的影响，设计了依照平行对称形式布置的机器人本体结构。

图1 仿蟹机器人样机Fig.1 Prototype of crablike robot

1.2 动力学模型建立

仿蟹机器人在运动过程中，处于支撑相的步行足一端与躯体相连，另一端与地面接触，形成了封闭的运动链。对于这样一个串并联混合机构，其控制的本质就是如何来协调24个关节的运动，显然这是一个复杂冗余驱动问题。此外，脚力和关节扭矩可通过运动链从一条步行足传递到另一条，即存在严重的动力学耦合，无疑增加了机器人动力学模型建模的复杂性。下面简要介绍仿蟹机器人动力学模型的建立过程。

由于仿蟹机器人的单条步行足可简化为具有三个自由度的3关节串联机械臂，因此可得第i条步行足的拉格朗日动力学方程为

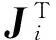
(1)

式中：qi=[θi1θi2θi3]T，为步行足i的关节转角矢量；Mi为惯性矩阵；hi为哥式力和离心力向量；gi表示重力矢量；Ji为步行足i的雅克比矩阵；τi为步行足i的关节扭矩矢量；fi为步行足i所承受的地面反力；当步行足处于摆动相，fi=0，在给定各关节转角的情况下，步行足i各关节所承受扭矩可以通过式(1)直接求得。

仿蟹机器人三足或多于三足处于支撑相时，可列出6个力/力矩的平衡方程，但未知足端反力的数目明显大于6，且随着支撑足数目的增加而增多，显然关于脚力的解有无数个，因此不能根据力平衡方程求解获得关节扭矩的控制变量。这其实是多足机器人脚力分配问题(数学规划问题)，而且它的约束也很复杂，其中包括：机体力平衡、脚底法向力非负、脚底切向力小于静摩擦力、每个关节承受力矩必须在驱动器额定范围内。关于如何进行脚力分配，国内外学者针对多支链运动机构的脚力分配控制，提出了一些规划算法，如：线性规划法(linear programming, LP)、解析法、平方规划法(quadratic programming, QP)、对偶线性规划法(compact-dual linear-programming, CDLP)、伪逆法等[11]。因脚力规划方法不是本文研究重点，没有进行深入的探讨，直接选用了一种可满足运算实时性的伪逆法作为本文脚力分配算法。

采用伪逆法进行最优脚力分配，根据优化目标函数的不同可分为以下两种：1)以内力平方和最小化作为优化目标；2)以关节扭矩平方和最小化作为优化目标。文献[14]证明了在相同速度和占地系数的情况下，力矩优化分配策略在降低系统能耗方面更具有优势。因此本文直接对仿蟹机器人的关节扭矩进行优化分配。

图2为仿蟹机器人运动过程中的受力分析示意图，每条腿由多个连杆和足端构成。分析受力时，假设足端与地面铰链联接，机器人接触力的动力学方程可表示为

AF=-W

(2)

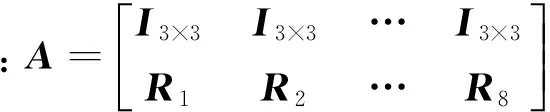
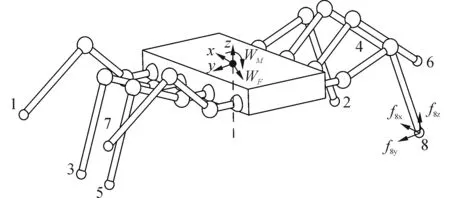
图2 仿蟹机器人受力分析图Fig.2 Force system acting on crablike robot

利用单步行足速度雅克比矩阵可获得足端反力和关节扭矩之间的变换公式为

F=J·τ

(3)

将式(3)代入到式(2)中可得

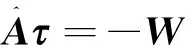
(4)

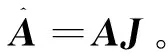
上述静不定问题可使用伪逆法求得关节扭矩的最小规范解：

(5)

为验证脚力分配方法的可行性，以波形步态为例进行仿蟹机器人脚力分配，如图3所示为一个迈步周期下八条步行足24个关节的力矩分配结果。从关节力矩分配结果可以看出，在机器人运动过程中，膝关节承受的负载力最大，髋关节承受力矩最小，但在支撑相下通常不为0。由于机器人在行走过程中支撑足和摆动足的数目是不断变化的，因此在某条步行足抬起或者落下的瞬间，足力分配的结果是不连续的，如果要使机器人在行走过程中消能耗降低，应尽量使力平均分配到各支撑足上。可见其与真实机器人行走过程中的规律完全相符，从而验证了脚力分配理论的正确性。

1.3 能耗模型建立

仿蟹机器人的每一个关节皆由直流电机和一个蜗轮蜗杆传动机构构成，对于这样一个模型，一个步态周期关节电机的功率损耗为

(6)

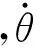
式(6)中第一项为机械能损耗、第二项为驱动系统在传动机构中的热损耗。由于仿蟹机器人步行足与环境间的相互作用，机械能可能出现负的情况，但是电机不能吸收负功，因而当机械能做负功时，机械能会以热量的形式耗散掉，因此，式(6)可改写为

(7)

其中

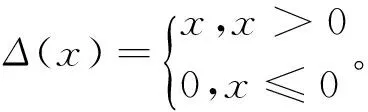
对于仿蟹机器人的系统能耗为所有24个关节能耗之和，可用下式进行计算：

(8)

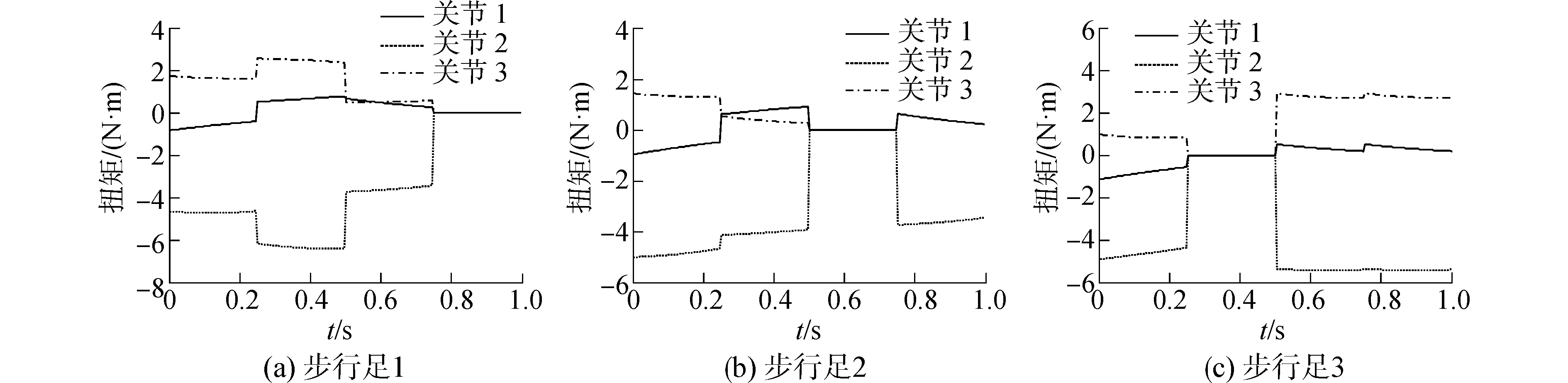
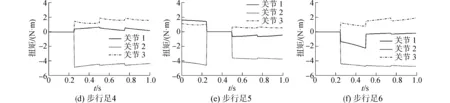
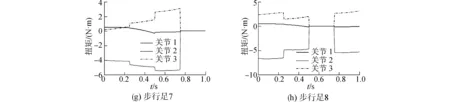
图3 仿蟹机器人关节扭矩分配曲线Fig.3 Graphs of joint torques with torque distribution of crablike robot

1.4 行走稳定性判定方法

采用准确的参数评定仿蟹机器人的行走稳定性，对于机器人的步态拟定、足尖点轨迹规划和抗干扰性都是至关重要的。对于多足机器人最常采用的稳定性判定方法为McGhee等于1968年提出的重心投影法，该方法将机器人重心在水平面的投影到落地足所形成的支撑多边形边界的最短距离作为稳定裕量衡量准则。基于几何概念的稳定性判定准则忽略了机体高度对于稳定的影响，而且只能应用在平坦的路面上，具有很大的局限性。为了个更好的描述多足机器人的稳定性，Messuri等于1985年提出了规范化能量稳定裕量(normalized energy stability margin, NESM)，该方法将机器人当前势能与倾倒过程中最大势能差作为稳定裕量的衡量准则，无论对于平坦路面还是非平坦路面都是最适宜的，其计算公式为[17]

(9)

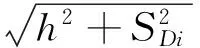
(10)

式中：h为机器人质心到支撑面的距离，SDi为重心在支撑面的投影点到支撑边线的最短距离，θ表示水平面与支撑平面之间的角度，εr水平面与旋转轴线之间的夹角，εi为旋转周线在支撑面内的投影与支撑面内水平线之间的夹角。

式(10)中的变量除了SDi外，其余参数均可通过传感器直接测量得到。通过分析变量SDi的物理意义可知它与静态稳定边界(SSM)是等价的，因此借鉴静态稳定裕量的计算原理。当机器人沿径向轴做单向运动，后向稳定裕量最小值出现在机体后侧的步行足由后极限位置抬起的瞬间；前向稳定裕量最小值出现在机体前侧步行足摆动到前极限位置落地瞬间，而SSM为前向稳定裕量和后向稳定裕量的最小值。由于篇幅限制，本文没有给出推导过程，直接给出仿蟹机器人采用等相位增加步态(constant phase increment gait)运动时的的SDi的计算公式：

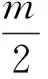
(11)

(12)

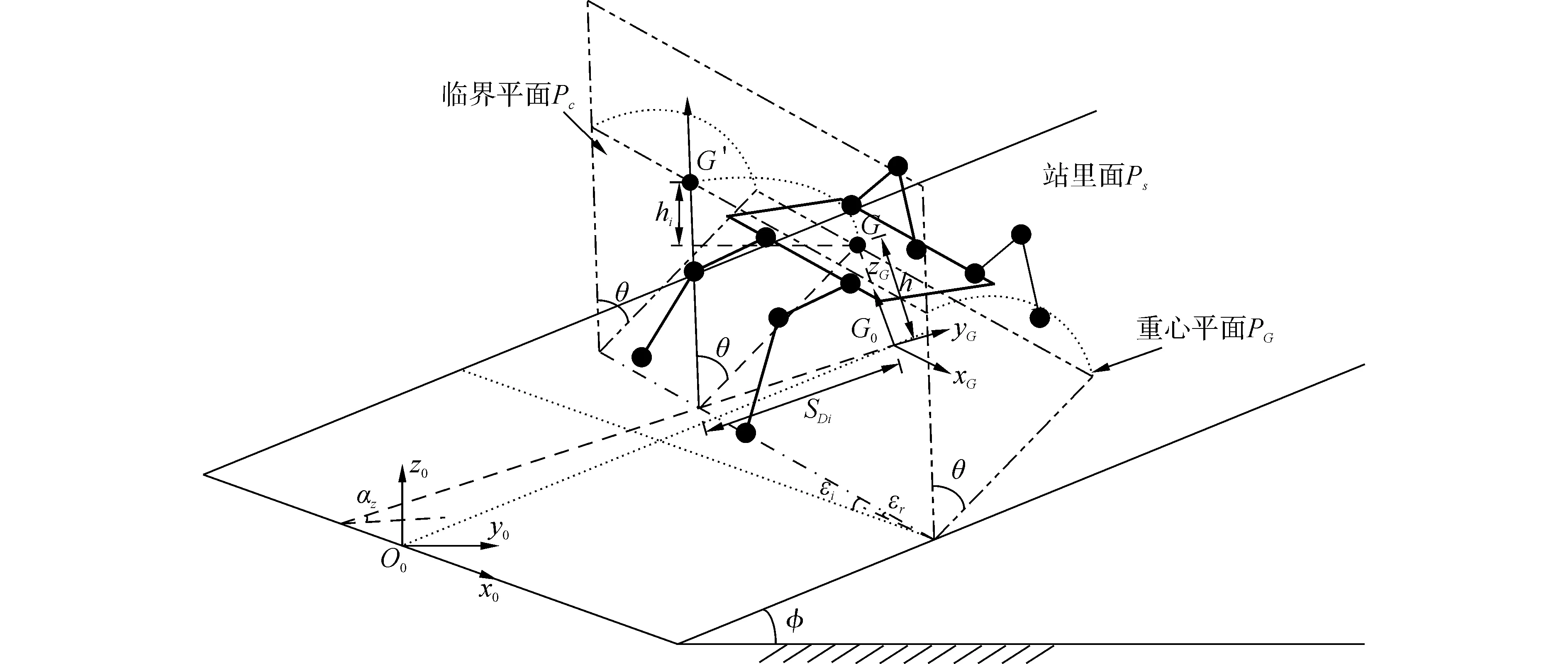
图4 仿蟹机器人静态稳定裕度计算简图Fig.4 Calculation diagrams of static stability margin for crablike robot

(13)

(14)

式中：φ为机体同侧相邻步行足之间的运动的相位差，m为机器人躯干的宽度，L为步行足自然伸展长度，R为单步行程，β为占地系数。

2 仿海蟹机器人运动性能分析

本节基于前文建立的系统能耗和稳定性模型对仿蟹机器人的步态性能进行仿真分析。文献[18]针对大占地系数情况(对于六足机器人β≥2/3、对于八足机器人β≥3/4)，探讨了机器人步态参数对系统能耗和运动稳定稳定性的影响，得出机体同侧相邻足之间的摆动相位差对系统能耗影响较大。如果摆动相相位在一个步态周期内分配不合理，可能导致机器人效率急剧降低，因此本文针对大占地系数情况，研究步态参数对仿蟹机器人系统能耗和运动稳定性的影响。研究中用φ代表机体同侧相邻步行足之间相位差，为了消除静稳定性较差的支撑状态，即保证相邻步行足不能同时处于摆动相，相对相位φ应满足1-β≤φ≤β/3，其中当φ=1-β时对应的步态为波形步态，随着φ的增加，机体同侧四条步行足摆动相时间在一个步态周期内分布逐渐均匀，当φ=β/3达到完全均布。

2.1 步态参数对系统能耗的影响

仿蟹机器人在运动过程中单步行程R、运动速度v、占地系数β和摆动相时间ta之间的关系为

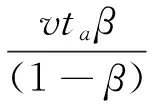
(15)

在多足机器人研究中一般将摆动相时间ta固定为常值，因此在研究步态参数对系统能耗的影响时，主要探讨单步行程、速度和占地系数变化的影响。

研究步长恒定时，相对相位、爬行速度和占地系数对仿蟹机器人横行步态能耗的影响。仿真过程中机器人机体与地面保持平行，运动方向沿y轴正方向，机体与地面之间的高度始终保持h=0.18 m，步长保持R=0.16 m，占地系数从最小值0.75增加到0.90。针对不同占地系数，依次对机器人进行仿真。表1所示为仿真中用到的机器人本体参数，取地面摩擦系数μ=0.35。

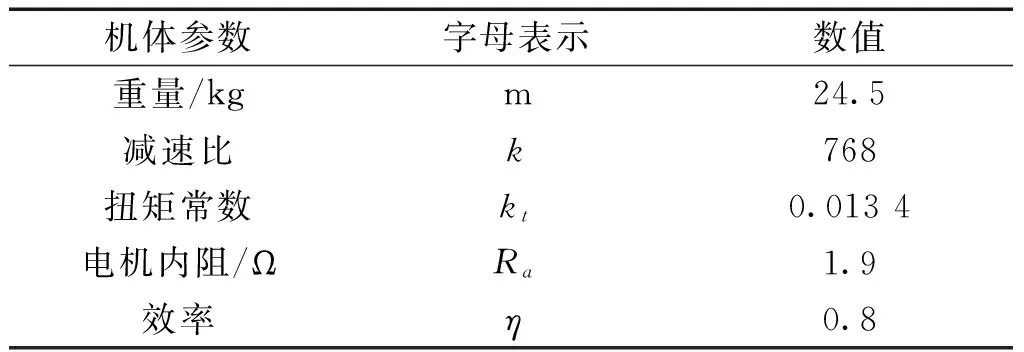
表1 仿蟹机器人主要仿真参数

仿蟹机器人采用三种步态运动(相对相位φ不同)，仿真得到的平均功率损耗曲线如图5(a)、(c)、(e)所示。由图可知，对于三种不同步态，当占地系数恒定时，随着机器人爬行速度的增加平均功率损耗基本保持不变或小幅度的升高。机器人的运动速度越慢，系统的功耗越低，但是速度的降低同样也会使机器人通过一段固定距离所花费的时间变长，因此机器人总的能耗也可能增加。可见，用平均功率损耗的大小来衡量机器人效率并不准确。在此引入另外一个衡量机器人能耗的物理量——能耗比，其物理意义是：使单位质量的物体移动单位距离所耗费的能力。能耗比越大表明机器人的能耗越大，反之机器人的能耗越小。三种不同步态对应的能耗比曲线分别5(b)、(d)、(f)所示。由图可知，对于一个特定的占地系数，仿蟹机器人的能耗比随着爬行速度的增加而逐渐降低的，且占地系数越大机器人的能耗比越小。这一点很容易理解，随着占地系数增加，支撑相足的数目也相应增加，机器人的重量和负载力分摊单一支撑足上的力分量相应也会降低，根据机器人单腿动力学计算公式可知关节承受的扭矩相应也会减少，因此系统能耗降低。

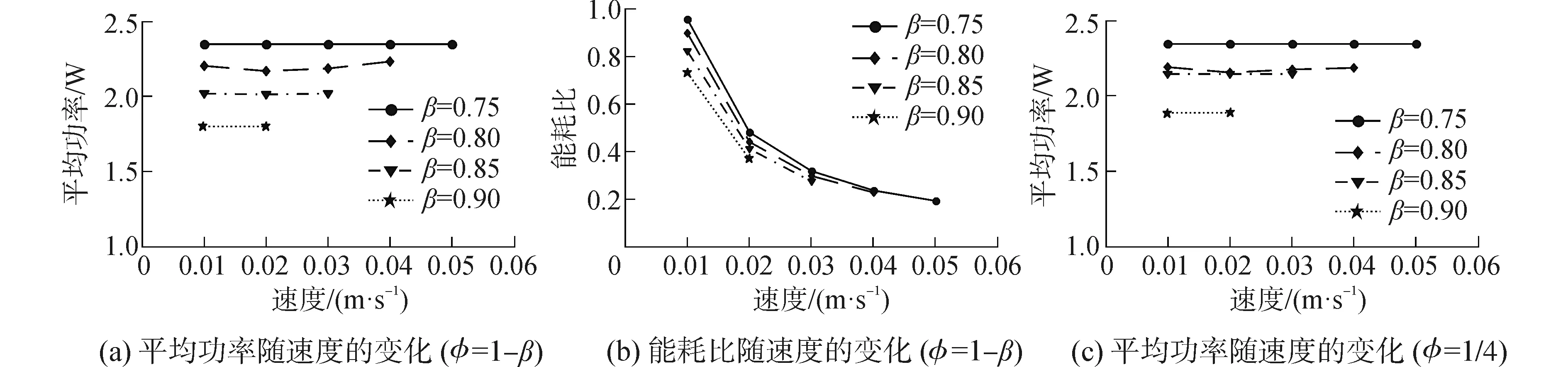
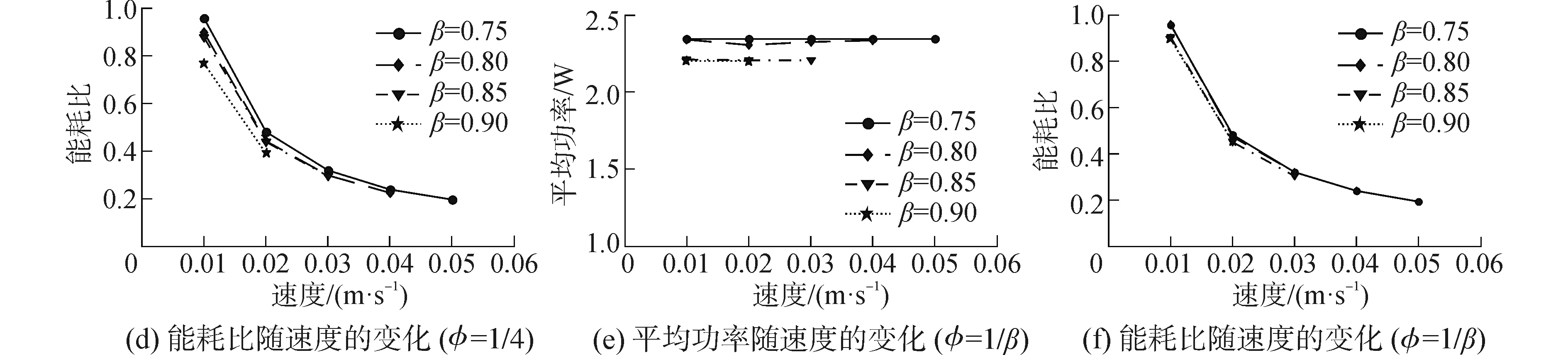
图5 三种步态平均功率和能耗比随速度的变化Fig.5 Variations of average power consumption and specific energy with velocity for four duty factor of three gaits

研究相对相位对系统能耗的影响。由图可知，随着相对相位φ的增加，大占地系数能耗比曲线逐渐向小占地系数能耗比曲线汇聚。当相对相位达到最大值时，几个能耗比曲线基本重合，即对于同一占地系数，随着相对相位的增加机器人的能耗升高。可见，机体同侧步行足摆动相时间在一个步态周期内分布越均匀，机器人的运动效率越低。对于横向行走的八足仿蟹机器人来说，机体同侧相邻步行足先后摆动的时间间隔增加，会导致机器人的运动效率降低。图5中没有给出机器人高速运动、大占地系数情况下的能耗比，其主要原因是：当占地系数较大时，步行足的摆动速度也会相应提升，但是实际机器人关节运动受到驱动器自身动力学特性约束，存在一个最高运行速率，而在此组步态参数下，机器人关节摆动速度超出了驱动器的极限转速。综上所述，仿蟹机器人采用波形步态横向行走时运动效率最高，与效率最低的步态(相对相位φ=β/3)相比可节能4%～25%。

2.2 步态参数对NESM的影响

利用Matlab软件对仿蟹机器人进行运动仿真，得到了三种横行步态的NESM随占地系数β和步长R的变化曲线如图7所示。

研究机器人运动速度恒定时，相对相位、步长和占地系数对仿蟹机器人横行步态能耗的影响。图6所示为机器人速度为0.02 m/s，三种步态能耗比随占地系数的变化曲线。由图可知，对于所有占地系数，能耗比均随着机器人迈步步长的增加而升高。其原因是：当机器人的迈步步长较大时，处于支撑相步行足的足端相对于机体质心偏置距离增加，相应的关节需要提供更大的扭矩以支撑机体的重量，因此机器人的能耗增加。通过对比不同占地系数机器人的能耗比曲线，可得到与上面相同的结论，随着占地系数的增加，机器人能耗降低。对比图6(a)、(b)和(c)可知，波形步态能耗最低，随着相邻步行足摆动时间间隔的增加，机器人的能耗升高。

由图可知，当占地系数恒定时，三种步态的运动稳定性均随着步长的增加而变差，然而对于特定的迈步步长，随着占地系数的变化，三种步态的NESM变化规律并不一致。由图8(a)可知，机器人采用波形步态运动时(φ=1-β)，随着占地系数的增加，机器人的NESM逐渐减小；由图8(b)、(c)可知，另外两种步态运动稳定性的变化规律与波形步态正好相反，即随着占地系数的增加，运动稳定性逐渐得到改善；当占地系数增加到足够大时，无论迈步步长如何变化，NESM提高的很少，NESM曲线基本达到水平，出现这种情况主要是当占地系数较大时，处于支撑相步行足的数目增多，步长对稳定性影响变小。通过对比图7(a)、(b)和(c)可知，对于横行的八足仿蟹机器人而言，波形步态稳定性是最差的。当相对相位达到最大值(φ=β/3)时对应的步态稳定性最佳，与波形步态相比NESM可提升3%～25%。可见，随着相对相位φ的增加，机器人的运动稳定性逐渐得到改善。

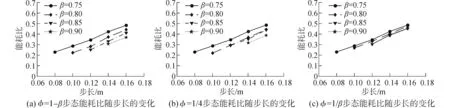
图6 三种步态能耗比随步长的变化Fig.6 Variations of specific energy with stroke for three duty factor

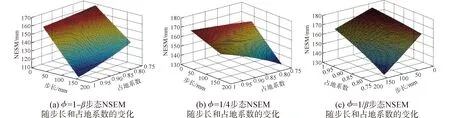
图7 三种步态NESM随步长和占地系数的变化Fig.7 Variations NESM with stroke for three duty factor

3 步态实验研究

为验证前面理论分析的正确性，搭建了仿蟹机器人实验平台，如图8所示。该实验平台包括dSPACE接口板、工控机、仿蟹机器人样机、陀螺仪、电压电流实时采集模块。其中工控机和dSPACE半物理仿真平台主要负责采集仿蟹机器人驱动系统的瞬时电压、瞬时电流和机器人的瞬时姿态角。

实验环境为硬质水泥地面，占地系数取β=5/6，对三种步态分别进行实验，其中每种步态实验过程持续四个完整步态周期。实验得到的驱动系统功耗和机器人姿态角随时间的变化曲线分别如图9和10所示。

由图9(a)可知，随着相对相位φ的增加，机器人功率波动幅度减小，但功率曲线整体上移。由图9(b)可知，随着相对相位φ的增加，机器人的平均功率损耗增加，因此机器人的效率降低。将实验结果代入能耗比计算公式，得到三种步态的能耗比分别为17.9、20.4和24.2，能耗比随相对相位的变化规律与理论分析得到的结论一致。当占地系数β=5/6，通过合理的选择相邻步行足运动的相对相位最多可节能23.2%。由图10可知，随着相对相位φ的增加，仿蟹机器人的翻滚角和俯仰角波动幅度增大，表明随着相对相位的增加，机器人躯干的波动幅度随之增大，抗干扰的能力降低，因此其运动稳定性变差，与理论分析结果一致，验证了前面理论分析的正确性。

图8 仿蟹机器人行走性能测试实验Fig.8 Testing on the walking properties of crablike robot

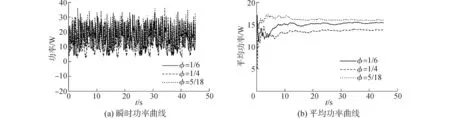
图9 机器人驱动功率曲线Fig.9 Driving power curves of the robot

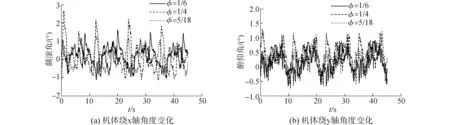
图10 机器人姿态曲线Fig.10 Posture curves of the crablike robot

4 结论

1) 当仿蟹机器人的步长和占地系数恒定时，随着步进速度的增加，系统能耗降低；当步长和步进速度恒定时，随着占地系数的增加，支撑足数目相应增多，机体重量在各支撑足上分配更加均匀，机器人系统能耗降低。

2) 当仿海蟹机器人的步进速度和占地系数恒定时，随着迈步步长的增加，步行足足端相对于机体质心偏置距离增加，支撑足的各关节需要提供更大的扭矩以支撑机体的重量，导致系统能耗升高。

3) 当相对相位φ=1-β时，仿蟹机器人的步态稳定性随着迈步步长和占地系数的增加而变差；当相对相位φ≥1-β时，随着占地系数的增加，机器人的步态稳定性逐渐得到改善。

4) 随着机体同侧相邻步行足相对相位的增加，仿蟹机器人的运动效率降低，但稳定性有所改善。在特定的步进速度和步态占地系数下，通过合理选择相对相位能够使系统能耗节省20%～30%。

[1]SOYGUDER S, ALLI H. Kinematic and dynamic analysis of a hexapod walking-running-bounding gaits robot and control actions[J]. Computers and electrical engineering, 2012,38(2): 444-458.

[2]金波，陈诚，李伟.基于能耗优化的六足步行机器人力矩分配[J].浙江大学学报：工学版, 2012, 46(7): 1167-1174.

JIN Bo, CHEN Cheng, LI Wei. Optimization of energy-efficient torque distribution for hexapod walking robot[J]. Journal of Zhejiang University： engineering science, 2012, 46(7): 1167-1174.

[3]KIM H, LEE J. Design, swimming motion planning and implementation of a legged underwater robot (CALEB10: D.BeeBot) by biomimetic approach[J]. Ocean engineering, 2017, 130: 310-327.

[4]SEOK S, WANG A, MENG Y C, et al. Design principles for energy-efficient legged locomotion and implementation on the MIT cheetah robot[J]. IEEE/ASME transactions on mechatronics, 2015, 20(3): 1117-1129.

[5]金城. 具有半球形足端的六足机器人步态生成和能耗优化研究[D]. 杭州：浙江大学， 2012.

JIN Cheng. Gait generation and power consumption optimization of hexapod walking robot with semi-round rigid feet[D]. Hangzhou: Zhejiang University, 2012.

[6]王刚, 韩金华, 韩世凯,等. 基于CPG的仿蟹机器人复杂地形步态生成方法[J]. 中南大学学报:自然科学版, 2016, 47(12): 4070-4080.

WANG Gang, HAN Jinhua, HAN Shikai, et al. Gait generation method of crablike robot walking on complex terrain based on CPG[J]. Journal of Central South University: science and technology, 2016, 47(12): 4070-4080.

[7]王新杰，李培根，陈学东,等. 四足步行机器人动力学模型及脚力分配研究[J]. 华中科技大学学报:自然科学版, 2005, 33(12): 12-15.

WANG Xinjie, LI Peigen, CHEN Xuedong, et al. Dynamic model of quadruped robots and its force distribution[J]. Journal of Huazhong University: nature science edition, 2005, 33(12): 12-15.

[8]MARHEFKA D W, ORIN D E. Quadratic optimization of force distribution in walking machines[C]// Proceedings of the 1998 IEEE International Conference on Robotics & Automation, Leuven, Belgium: IEEE, 1998: 477-483.

[9]俞昌雄,干东英. 步行机能量效率问题的计算机辅助研究[J]. 机器人,1989, 3(5):43-48.

YU Changxiong, GAN Dongying. Computer aided study on energetic efficiencies of a walking vehicle[J]. Robot, 1989, 3(5): 43-48.

[10]ERDEN M S. Optimal protraction of a biologically inspired robot leg[J]. Journal of intelligent and robotic systems, 2011, 64: 301-322.

[11]ROY S S, PRATIHAR D K. Soft computing-based expert systems to predict energy consumption and stability margin in turning gaits of six-legged robots[J]. Expert systems with applications, 2012,39(5): 5460-5469.

[12]GONZALEZ P, ESTREMERA J, GARCIA E, et al. Optimizing Leg Distribution Around the Body in Walking Robots[C]// Proceedings of the 2005 IEEE, International Conference on Robotics and Automation, Barcelona, Spain:IEEE, 2005: 3207-3212.

[13]MAEHEFKA D W, ORIN D E.Gait planning for energy efficiency in walking machines[C]// Prcceedings of the 1997 IEEE International Conference on Robotics and Automation, Albuquerque, New Mexico: IEEE, 1997: 474-480.

[14]ROY S S, PRATIHAR D K. Dynamic modeling, stability and energy consumption analysis of a realistic six-legged walking robot[J]. Robotics and computer-integrated manufacturing, 2013, 29(2): 400-416.

[15]ROY S S, PRATIHAR D K. Effects of turning gait parameters on energy consumption and stability of a six-legged walking robot[J]. Robotics and autonomous systems, 2012, 60(1): 72-82.

[16]CHEN X, WANG L Q, YE X F, et al. Prototype development and gait planning of biologically inspired multi-legged crablike robot[J]. Mechatronics, 2013, 23(4): 429-444.

[17]王立权，王海龙，陈曦. 八足仿蟹机器人行走稳定性分析[J]. 中南大学学报:自然科学版, 2014, 45(10): 3416-3422.

WANG Liquan, WANG Hailong, CHEN Xi. Walking stability analysis of an octopod crab-like robot[J]. Journal of Central South University: science and technology, 2014, 45(10): 3416-3422.

[18]ERDEN M S, LEBLEBICIOGLU K. Analysis of wave gaits for energy efficiency[J]. Autonomous robots, 2007, 3(23): 213-230.

本文引用格式：

韩金华, 王海龙, 王刚, 等. 仿蟹机器人横行步态运动稳定性及能耗分析[J]. 哈尔滨工程大学学报， 2017， 38(6)： 898-906.

HAN Jinhua， WANG Hailong， WANG Gang， et al. Stability and energy consumption of laterally walking gait in crablike robots[J]. Journal of Harbin Engineering University， 2017， 38(6)： 898-906.

Stability and energy consumption of laterally walking gait in crablike robots

HAN Jinhua1， WANG Hailong2， WANG Gang3， YE Xiufen1， WANG Liquan2

(1.College of Automation, Harbin Engineering University, Harbin 150001, China; 2.College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China; 3.Science and Technology on Underwater Vehicle Laboratory, Harbin Engineering University, Harbin 150001, China )

To enhance the motion stability of laterally walking gaits and reduce systematic energy consumption in a crablike robot, the normalized energy stability margin and energy consumption ratio were set as indicators to evaluate gait and pace and gait parameters. Based on dynamic analyses, multi-constrained equations of the tip-point force distribution were derived and a pseudoinverse method was used to optimize torque distribution in all robot joints. Considering the mechanical energy cost and energy loss due to heat emission in a DC motor, a mathematical model for obtaining energy consumption ratio of a crablike robot was formulated. Based on the commonly used constant-phase increment gait approach for a multi-legged robot, the influence on systematic energy consumption and the motion stability, duty factors, stroke, and relative phase of ipsilateral adjacent legs were analyzed in detail. Results show that while the motion efficiency of a crablike robot decreases with increasing relative phase of the ipsilateral adjacent legs, its motion stability improves. Thus, using specific walking speed and duty factors and by rational selection of the relative phase, systematic energy consumption in crablike robots can be reduced by 20%～30%.

crablike robot; energy consumption ratio; normalized energy stability margin(NESM); gait planning; stability; walking gait; laterlly walking

2016-04-07. 网络出版日期：2017-05-03.

国家自然科学基金青年基金项目(51409058)；黑龙江省博士后基金项目(LBH-Z15035)；黑龙江省自然科学基金项目(F201005).

韩金华(1966-), 女, 工程师,博士后； 王海龙(1988-), 男, 博士研究生.

王海龙，E-mail:wanghailong0726@hrbeu.edu.cn.

10.11990/jheu.201604018

http://www.cnki.net/kcms/detail/23.1390.u.20170503.1753.004.html

TP242.6

A

1006-7043(2017)06-0898-09