一种滑动摩擦弹性非相似接触问题直接求解方法研究
2017-07-07陈重华吴远波
陈 汀,陈重华,吴远波
(上海卫星工程研究所,上海 201109)
一种滑动摩擦弹性非相似接触问题直接求解方法研究
陈 汀,陈重华,吴远波
(上海卫星工程研究所,上海 201109)
针对传统方法在求解滑动摩擦条件下弹性非相似接触问题时存在多项式积分过多的问题,提出了一种直接求解方法。建立了弹性非相似体接触问题的模型,用修正的高斯-雅可比积分公式求解奇异积分方程,可求得接触表面上的接触应力和与疲劳相关的平面应力。因计算中不含积分过程,所提方法能更有效、更直接地求解滑动摩擦条件下弹性非相似接触问题,且计算过程可用于其他类型的接触问题。用一个算例,通过与精确解的比较验证了方法的有效性。计算了圆柱型压头与弹性半平面在滑动摩擦条件下的接触应力分布实例,分析了摩擦因数对接触表面应力分布的影响规律,探讨了接触表面产生裂纹的可能原因。结果发现:接触面的摩擦效应导致接触区质心向接触区尾翼偏移,偏移量随摩擦因数增大而变大,这会产生偏移力矩,而法向接触力与接触区长度近似呈抛物线型的变化关系。研究对设计实际工程中具抗疲劳性能的零部件有理论价值和指导意义。
接触刚度; 非相似接触问题; 滑动摩擦; 接触应力; 平面应力; 多项式积分; 修正的高斯-雅可比积分公式; 圆柱型压头
0 引言
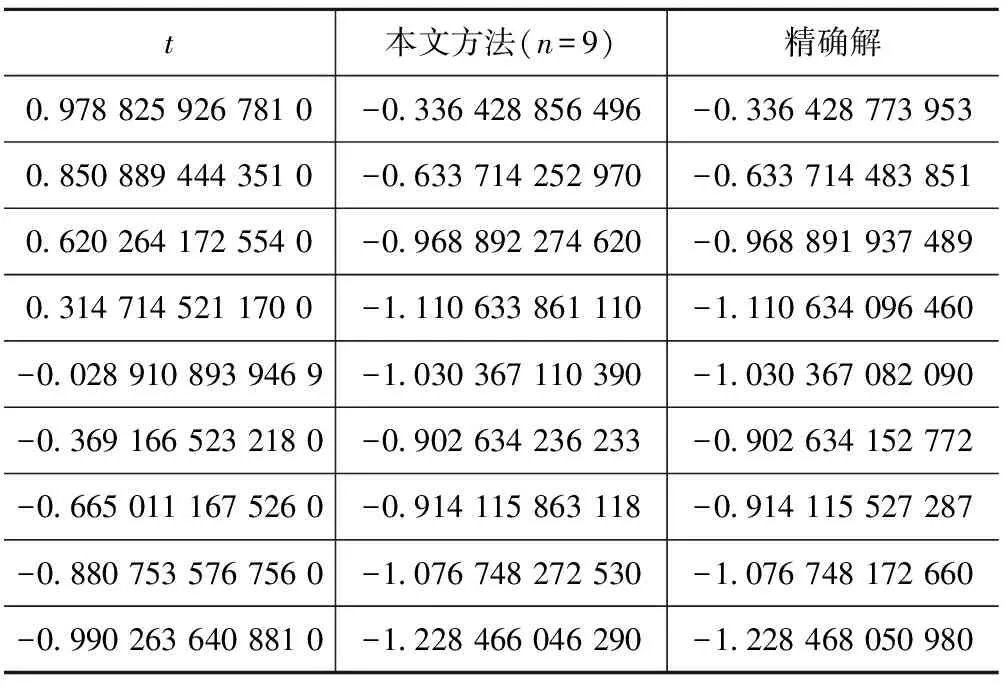
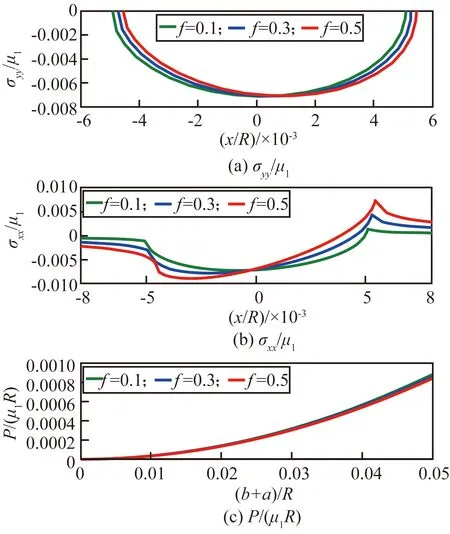
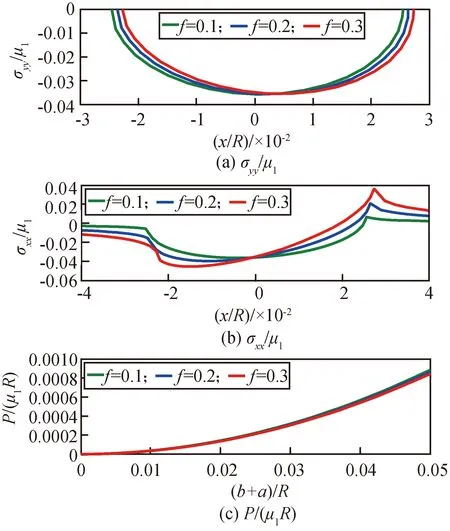
对摩擦接触问题,当作用于接触体表面切向力Q满足Q 通常,用于求解摩擦非相似材料接触问题的方法主要有有限元法和边界积分方程法两种。有研究用通用有限元求解器计算了无摩擦和有摩擦的接触问题[3-5]。虽然有限元法可有效用于求解任意复杂几何的接触问题,但它需对数据进行大量且繁琐的前后处理,处理方式的不同对分析结果有较大的影响。边界积分方程同样广泛用于求解此类接触问题[6-10]。与有限元方法不同,边界积分方程法能更方便、更有效且更直接地求解问题。虽然边界积分方程法已用于求解一些特别简化的模型,但仍缺乏一个完备且系统的求解非相似弹性体接触问题的理论框架[11-13]。为此,本文提出了一种基于修正的高斯-雅可比积分公式求解非相似弹性体接触问题的方法,研究了摩擦力对接触应力分布的影响规律。本文提出的方法能有效体现滑动摩擦接触条件下接触应力的渐进行为特征,并基于计算得到的接触应力,可推断产生疲劳和断裂问题的接触部件的表面裂纹产生的可能原因。 弹性压头与非相似的弹性半空间的摩擦滑动接触问题如图1所示。 图1 一般接触问题的几何描述Fig.1 Geometry of general contact problem 压头轮廓的几何形状表示为y=h(x)。因载荷与坐标z无关,故该接触问题可简化为一个二维平面接触问题。外加切向载荷Q和法向载荷P使压头处于一种极限平衡状态,或以恒定速度运动。由于该运动很慢,可忽略动态效应的影响。 设在切向应力p(x)和法向应力q(x)的共同作用下,接触表面上任一点在x、y向的位移分别为uxi,uyi(其中:i=1表示半平面;i=2表示压头),则由文献[6],在接触表面上的任一点,接触表面的位移和表面上的法向与切向接触应力的关系可表示为 (1) (2) 式中:υi为泊松比。 在与弹性压头相连的运动坐标系中,存在以下边界条件 (3) (4) 式中:uy为半空间表面上任意一点的法向位移;D为两接触弹性体的相互趋近量。 在接触区域(-a,b)内存在摩擦法则 (5) (6) 式(5)、(6)构成了一对关于未知接触应力σ,τ的积分方程。对本文讨论的问题,法向接触力p(x),-a (7) 式中: 此处:χ*为常数,表征两接触体材料弹性非相似性的程度;Ei,υi,μi分别为弹性模量、泊松比和接触体的剪切模量;i=1,2。 为获取该接触问题的完备解,需要其他附加条件。首先,p(x)必须满足 (8) 式中:P为外加法向力。外加力的幅值可通过外加力P或沿y轴的压头位移表征;在接触区的端点-a,b处,不论接触光滑与否,切向接触应力p(x)的解须满足某种协调条件。 (9) 正规化后,外力与接触应力分布的平衡方程变为 (10) 基于多项式的正交特性,奇异积分方程可转化为一系列关于未知系数的代数方程。此方法可有效保证解的收敛性和稳定性。但由于所含的积分计算过多,导致求解时间很长。为改善这一缺陷,一种更实用的方法是利用基于修正的高斯-雅可比积分公式[7-8]。与多项式序列法不同,修正的高斯-雅可比积分公式不含积分计算,因而可更直接地求解。 本文用修正的高斯-雅可比积分公式求解奇异积分方程。首先,由文献[2],定义复势函数 (11) 此势函数的基本解可定义为 (12) 式中:常数κ=-(α+β)为基本解ω(s)的指数。 式(11)的通解可表示为 (13) 式中:g(s)为区间[-1,1]中的一个连续的有界函数。 对式(13)应用修正的高斯-雅可比积分公式,有柯西核的奇异积分方程可表示为 (14) 将式(14)代入式(9),常规运算后可得 (15) 用配点法并令配点中仅有有限个积分点,即s=si。此处:si为以下雅可比多项式的根 (16) 式(10)可化为代数方程 (17) (18) 式中: (19) 以上基于修正的高斯-雅可比积分公式的非相似弹性体的摩擦滑动接触问题的求解过程同样适于求解其他类型的接触问题,包括在接触区域端点处未知函数为有限值或无穷的情形[14]。 在求解式(15)获取法向接触应力p(x)后,其余的场变量可由p(x)及合适的格林函数,用以下方程确定 (20) 影响函数对所有不存在于边界上的点都是正规的[6]。 通过p(x)不仅可直接计算接触表面上的接触应力σyy(x,0),σxy(x,0),而且能求得因与疲劳相关而引起广泛关注的接触表面上的平面应力σxx(x,0),它与接触表面的表面裂纹产生密切相关[15-16]。获取接触表面的接触应力σyy(x,0),σxy(x,0),接触表面的σxx(x,0)可用应力-位移关系求得,有 (21) 用本文方法计算一个算例,并与解析解进行对比,以验证本文算法的有效性。算例取自文献[17],并做了微小的改动。算例的物理问题描述为:具尖角的粗糙压头在弹性非相似半空间表面有摩擦地滑动。考虑此问题的物理特性,它对应于κ=1的弯曲接触问题,分量α,β满足 (22) 积分方程变为 (23) 并满足条件 (24) 式中:L与外载荷相关的参数。 该有界未知方程的解析解为 (25) 设数值计算的参数条件为:α=-0.34,β=-0.66,L=π/sin(απ)。在MATAB 7.0软件中对本文算法编程,本文方法的计算结果与精确解的对比见表1。 表1 本文方法的计算结果法与精确解对比(n=9) 由表1可知:本文方法的计算精度非常高,与精确值的误差小于1×10-7,表明本文算法可有效且准确地计算所讨论的接触问题。为进一步验证本文方法的有效性,以下对具体的接触算例进行计算。 4.1 问题描述 对工程设计中常用的圆柱型压头与弹性非相似半平面的接触问题进行计算。相关接触问题如图2所示。 图2 圆柱型压头与非相似弹性半空间摩擦滑动接触问题的几何描述Fig.2 Geometry of contact problem for a cylindrical stamp sliding on half-plane 压头的轮廓可表示为 (26) 故有 (27) 根据图3和式(7),积分方程式(9)可表示为 (28) 外力和接触应力的平衡条件可表示为 (29) (30) 由于在接触区端点x=-a,x=b处均为光滑接触,根据上述物理条件可知:α,β均为正实数,系统指数κ=-1,故有 f>0时 (31) α=0.5,β=0.5,f=0时 (32) f<0时 (33) 对此类接触问题,在外加法向力P作用下,接触长度a,b均未知。但对给定接触长度值,式(30)是关于n个未知参数g(tj)的n个方程组,即 a*(si-1)],i=1,2,…,n+1 (34) (35) 由此,可确定a*,b*的关系。 4.2 计算结果与讨论 本文提出的方法主要计算接触应力,接触表面的平面内应力σxx(x,0)及载荷-接触长度关系。 对如图2所示的圆柱型压头与非相似弹性半空间接触问题,设(a+b)/R分别为0.010,0.025,0.050;f分别为0.1,0.3,0.5;υ=0.3。与抛物线型压头不同,圆柱型压头与非相似弹性半平面在接触区域两端均光滑接触,因此法向接触压力在接触边界自然趋于零值。用本文方法计算的f对接触区域内接触表面应力的影响分别如图3~5所示。 图3 圆柱型压头与非相似弹性半平面接触时的接触应力分布(f=0.1,0.3,0.5;(b+a)/R=0.010)Fig.3 Contact stresses on surface of half-plane loaded by a cylindrical stamp (f=0.1,0.3, 0.5, (b+a)/R=0.010) 图4 圆柱型压头与非相似弹性半平面接触时的接触应力分布(f=0.1,0.3,0.5;(b+a)/R=0.025)Fig.4 Contact stresses on surface of half-plane loaded by a cylindrical stamp (f=0.1,0.3, 0.5, (b+a)/R=0.025) 图5 圆柱型压头与非相似弹性半平面接触时的接触应力分布(f=0.1,0.3,0.5;(b+a)/R=0.025)Fig.5 Contact stresses on surface of half-plane loaded by a cylindrical stamp (f=0.1,0.3, 0.5, (b+a)/R=0.050) 由图3~5可知:当x<-a时,σxx(x,0)为压应力;当x>b时,σxx(x,0)为拉应力。描述接触区位置的接触长度a,b事先未知,是随外加法向载荷P增大而单调递增的强非线性函数。在求解该接触问题时,首先假设初值a,b,然后根据压头的平衡条件计算外加法向载荷P,重复此过程即可求得外加载荷P与接触长度a+b的关系。有趣的是,法向接触力与接触长度a+b的关系曲线近似为抛物线,观察接触应力分布,可发现接触区的质心向接触区域的尾翼偏移。此偏移量随摩擦因数增大而变大。该现象使法向接触应力不再关于y轴对称,从而形成一个倾斜力矩。与抛物线型压头相似的是,摩擦因数变化对法向接触应力幅值σyy(x,0)的影响很小,但对平面内应力的影响显著。随着摩擦因数的增大,拉应力σxx(x,0)的峰值显著增大。在接触区前翼处的压应力和在尾翼处的拉应力均随摩擦因数增大而增大。 本文提出了一种求解滑动摩擦条件下的弹性非相似接触问题的有效方法。该法的优点是对不同类型的接触问题,都能有效而正确地获取接触应力的渐进行为特征。通过求解一个有尖角的粗糙压头与弹性非相似半平面的滑动摩擦接触问题并与精确解进行对比,验证了该方法的有效性,并讨论了一类典型的圆柱型压头与非相似弹性半平面的接触问题。研究结果表明:接触面的摩擦效应将导致接触区质心向接触区尾翼偏移,随着摩擦因数的增大,偏移量也逐渐增大,这将不可避免地产生偏移力矩,而法向接触力与接触区长度近似呈抛物线型的变化关系。本文研究可用于分析接触表面裂纹发生的可能原因,对设计实际工程中具抗疲劳性的零部件有重要的理论价值和指导意义。本文提出的方法的一个潜在应用是可用于求解部分滑动接触问题,后续将进一步研究。 [1] MINDLIN R D. Compliance of elastic bodies in contact[J]. Journal of Applied Mechanics, 1949, 16: 259-268. [2] GLADWELL G M L. Contact problems in the classical theory of elasticity[M]. Rockville: Sijthoff and Noordhoff, 1980. [3] AMBRICO J M, BEGLEY M R. Plasticity in fretting contact[J]. Journal of the Mechanics and Physics of Solids, 2000, 48: 2391-2417. [4] IYER K. Solutions for contact in pinned connections[J]. International Journal of Solids and Structures, 2001, 38: 9133-9148. [5] PORTER M I, HILLS D A. Note on the complete contact between a flat rigid punch and an elastic layer attached to a dissimilar substrate[J]. International Journal of Mechanical Science, 2002, 44: 509-520. [6] JOHNSON K L. Contact mechanics[M]. Cambridge: Cambridge University Press, 1985. [7] ERDOGAN F, GUPTA G D, COOK T S. Numerical solution of singular integral equations[M]// SIH G C. Method of Analysis and Solution of Crack Problems. Leyden: Noordhoff International Publishing, 1973. [8] KRENK S. On quadrature formulas for singular integral-equations of the first and second kind[J]. Q Appl Math, 1975, 33(3): 225-232. [9] MILLER G R, KEER L M. A numerical technique for the solution of singular integral-equations of the second kind[J]. Q Appl Math, 1985, 42(4): 455-465. [10] ERDOGAN F, GUPTA G D. On the numerical solution of singular integral equations[J]. Q Appl Math, 1972, 30(4): 525-534. [11] CHURCHMAN C M, SACKFIELD A, HILLS D A. Asymptotic solutions for contact problems: the effect of an internal discontinuity in surface profile[J]. Proc Inst Mech Eng C-J Mech Eng Sci, 2006, 220(4): 387-391. [12] SACKFIELD A, DINI D, HILLS D A. The tilted shallow wedge problem[J]. Eur J Mech Solid, 2005, 24: 919-928. [13] SACKFIELD A, DINI D, HILLS D A. Contact of a rotating wheel with a flat[J]. International Journal of Solids and Structures, 2007, 44: 3304-3316. [14] MUSKHELISHVILI N I. Singular integral equations: boundary problems of function theory and their application to mathematical physics[M]. New York: Dover Publications, 1992. [15] SURESH S, OLSSON M, GIANNAKOPOULOS A E, et al. Engineering the resistance to sliding-contact damage through controlled gradients in elastic properties at contact surfaces[J]. Acta Materialia, 1999, 47: 3915-3926. [16] LAWN B. Fracture of brittle solids[M]. Cambridge: Cambridge University Press, 1993. [17] MILLER G R, KEER L M. A numerical technique for the solution of singular integral-equations of the second kind[J]. Q Appl Math, 1985, 42(4): 455-465. An Efficient Solution Study for Elastically Dissimilar Contact Problems under Sliding Condition CHEN Ting, CHEN Chong-hua, WU Yuan-bo (Shanghai Institute of Satellite Engineering, Shanghai 201109, China) An efficient and straightforward technique based on the improved Gauss-Jacobi quadrature rule was studied for solving elastically dissimilar contact problems under sliding condition in the paper. The model of contact problem for elastically dissimilar contact problems was established. The singular integral equation was solved by the improved Gauss-Jacobi quadrature rule. The contact stress on the contact surface could be obtained, and so was the plane stress which was related to the fatigue. Because there is no integration process in the computation, the elastically dissimilar contact problem can be worked out by the method proposed more efficiently and directly. The computation can be applied to other types of contact problems. The effectiveness of the method proposed was proved by comparing with the exact value for some computation sample. The real contact problem for a cylindrical stamp sliding on a half-plane was calculated. The effect of frictional coefficient on the contact pressure distribution was analyzed. The possible reasons for crack initiation associated with fatigue and fracture of the contacting components were also discussed. It finds that the frictional effect on the contact surface will cause the centre of the contact area migrating to the end of the contact area. The migration will become bigger when the frictional coefficient is bigger. It will form migration moment. And the relationship of the normal contact force and the length of the contact area can be characterized by paracurve. This study has its theoretically value and reference meanings in designing the anti-fatigue parts in engineering. contact rigidity; disimilar contact problem; sliding condition; contact stress; plane stress; polynomial integral; improved Gauss-Jacobi quadrature rule; cylindrical stamp 1006-1630(2017)03-0066-07 2016-08-12; 2016-10-22 陈 汀(1984—),男,博士,主要研究方向为卫星总体设计、机械系统动力学。 TH113 A 10.19328/j.cnki.1006-1630.2017.03.0091 弹性非相似体建模

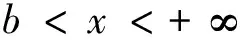
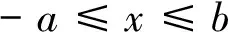
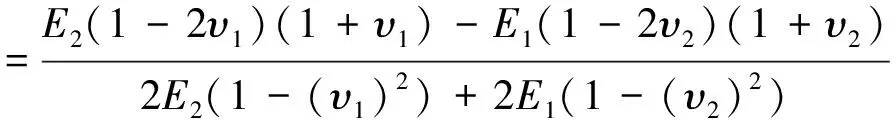
2 方程求解
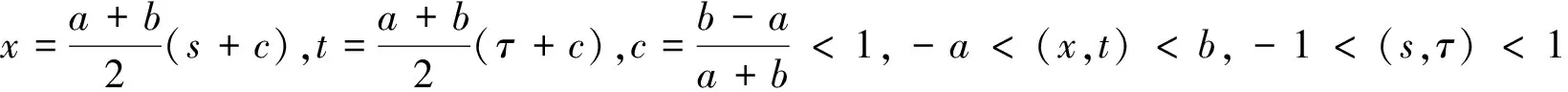




3 方法有效性验证
4 接触问题实例计算


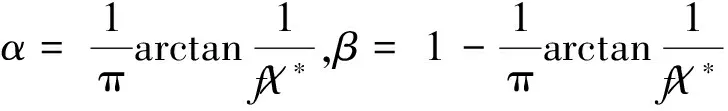

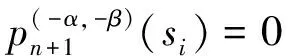
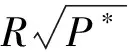

5 结束语
