红外扫描过采样系统点目标亚像元定位与灰度提取方法研究

林两魁,王少游,任秉文

(上海卫星工程研究所,上海 201109)



红外扫描过采样系统点目标亚像元定位与灰度提取方法研究

林两魁,王少游,任秉文

(上海卫星工程研究所,上海 201109)

为提高系统的目标测向精度，对一种红外扫描过采样系统对远距点目标亚像元定位和灰度提取方法进行了研究。根据扫描过采样成像特点和模型，给出了基于重心法和最小二乘量子粒子群优化(LS-QPSO)两种过采样点目标亚像元定位技术。前者直接求解过采样图像目标像斑的灰度加权重心，用于点目标亚像元定位；后者基于最小二乘准则建立点目标定位和灰度估计目标函数，引入量子粒子群优化算法求解高维非线性目标函数最优化，同时实现点目标亚像元位置和灰度估计。对LS-QPSO方法进行拓展以满足对多个邻近点目标分辨需求。仿真结果表明：过采样体制能实现对点目标的亚像元定位；两种方法均能实现对单个点目标的亚像元定位，LS-QPSO性能更优；拓展后的LS-QPSO能实现对邻近多目标的分辨。

点目标； 扫描过采样； 亚像元定位； 灰度估计； 最小二乘； 量子粒子群优化； 重心法； 空间邻近目标

0 引言

过采样是法国最先提出的一种遥感扫描成像新体制，旨在提高扫描相机的空间分辨率，并已成功用于SPOT-5遥感卫星[1]。该体制不改变光学系统配置，只将常规采样体制的一排线列像元替换成两排像元，在线列方向错开半个像元间隔排列，在扫描方向每隔半个像元瞬时视场(IFOV)采样1次，对过采样数据进行融合处理能获得分辨率优于常规采样的遥感图像，可有效提高空间遥感载荷的性价比。美国则将该体制用于空间红外搜索与跟踪(IRST)系统，如MSX卫星SPIRIT-III载荷、新一代空间红外扫描传感器等，以实现对高速运动目标(如空间轨道目标)的探测和快速确认[2-3]。

实际应用中，目标常距探测系统很远，可视为点目标。在常规采样体制下，点目标大部分能量被单像元捕获，目标的成像无尺度、大小等形状信息，无法进行亚像元定位。在过采样体制下，目标辐射能量被多个像元捕获，目标在图像中呈现像斑形态，提供了对目标亚像元定位的可能，有望进一步提高监视系统对目标测向的精度。现有文献集中于研究过采样对目标检测性能的影响，而对过采样的点目标亚像元定位研究基本未涉及[3-7]。因此，研究从过采样图像中提取出点目标的亚像元位置和高精度灰度信息，对提高IRST系统的探测性能有重要意义。

红外扫描过采样点目标亚像元定位和灰度估计方法有两种。重心法是典型的图像亚像元定位技术，因其简单有效在工程中有广泛应用[8-9]。但该方法的定位精度依赖于目标成像对称性，且只能定位目标亚像元位置，缺乏目标灰度估计能力，也不具备对多个邻近目标的分辨能力。为此，本文结合最小二乘(LS)准则和量子粒子群优化(QPSO)方法研究过采样点目标的亚像元定位可行性(LS-QPSO法)。建立LS点目标亚像元定位和灰度估计目标函数，针对该目标函数的高维非线性最优化问题，引入QPSO算法求解目标函数优化问题，实现对点目标的亚像元定位和灰度估计[10-11]。同时，针对实际应用中对多个空间邻近目标的分辨和定位需求(如目标齐射、飞行器编队等)，结合贝叶斯信息准则(BIC)定阶准则，对LS-QPSO方法进行拓展，以实现对多个邻近目标的分辨和亚像元定位及灰度估计[12]。

1 扫描过采样成像特点与模型

1.1 过采样与常规采样成像对比分析

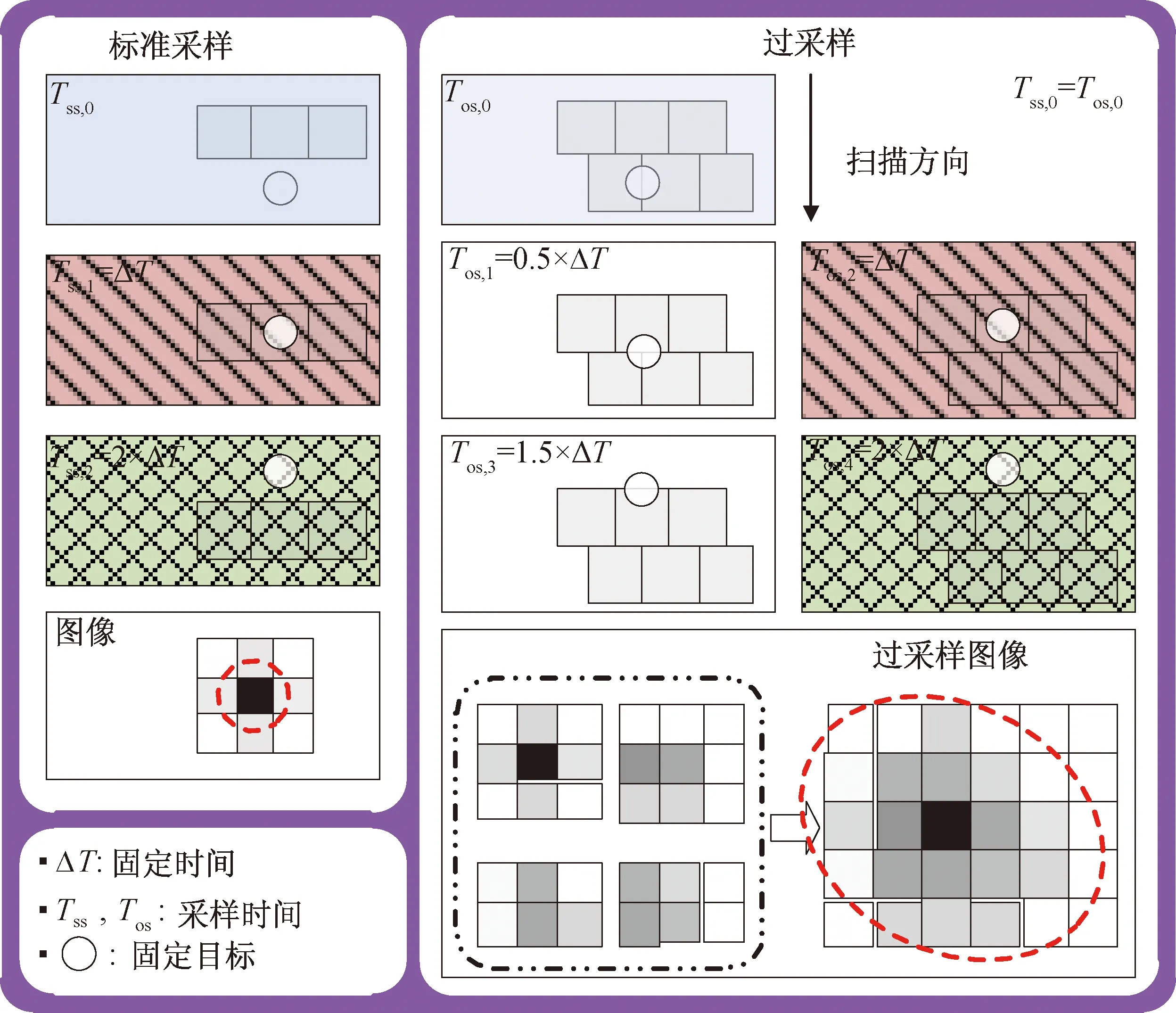
图1 常规采样与过采样的成像对比

扫描相机通过反射镜摆扫引导物空间光线聚焦到线列焦面使像元感光成像[3，13]。常规采样与过采样的比较如图1所示。常规采样体制的焦面线阵由单线列像元组成，扫描时在物空间视场每间隔1个IFOV各像元曝光成像1次，通过连续扫描获得二维图像。过采样探测体制采用错开半个像元距离并排的两列线阵焦平面结构，实现线列方向的空间过采样。扫描过程中，在扫描方向每扫过半个IFOV间隔，双线列像元即曝光成像1次，实现时间过采样。

由图1可知：与常规采样相比，过采样提高目标点落入像元中心的概率，从而提高目标的响应特性；通过时空双向过采样，还能将目标点能量4倍扩散到邻近像元，使目标在像平面上的成像呈现斑点形状特性。这种斑状成像特性为点目标的亚像元定位提供了可能。

1.2 点目标的过采样扫描成像模型

扫描相机对点目标的成像模型主要考虑三个因素：光学系统对入射光线的模糊效应、像元对目标辐射能量的离散采样，以及积分时间内因扫描镜运动而产生的运动模糊[6]。

一般采用点扩散函数(PSF)对光学系统成像建模。令(xi，yi)为目标i在像平面投影位置，σ为标准差，则PSF可表示为

(1)

假设线列各像元为正方形且尺寸相同，填充率为100%，像元长度d，像元中心 (xc，yc)。能量集中度(EOD)ce为当目标点落于像元中心时，该像元所捕获到的目标能量百分比[15]。有

(2)

将PSF在像元上积分可得该像元对点目标的响应

(3)

在像元曝光时间Ti内因扫描镜运动引起扫描方向运动模糊，假设运动a个像元，则运动模糊效果可表示为

(4)

像平面阵列由umax×vmax像元组成，设有目标N个，像平面投影坐标为(xi，yi)，i=1，2，…，N。则像平面的目标响应可表示为

Z=GS+N

(5)

式中：Z为umaxvmax维测量列向量；G为(umaxvmax)×N维导向矩阵，其元素由式(4)计算得到；S为目标在像平面上的辐射量向量；N为umaxvmax维噪声列向量。假定各像元噪声统计独立，服从零均值高斯分布，则各目标的信噪比(SNR)可表示为

(6)

式中：σn为噪声方差；si为目标i在像平面上的灰度值[6]。

2 基于重心法的点目标亚像元定位

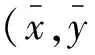
(7)

式中：sx，sy分别为目标像斑邻近区域P的灰度加权的x、y向位置；sP为区域P内的像元灰度和值。此处：

(8)

(9)

(10)

式中：s(x,y)为像元(x,y)处的灰度值。

由此可知：基于重心法的点目标亚像元定位计算方法简单，但无法直接估计点目标灰度值。

3 点目标分辨与定位的LS-QPSO方法

3.1 点目标亚像元定位与灰度估计目标函数

假定目标个数已知为N(N≥1)，由式(5)扫描成像模型，构建基于LS准则的目标亚像元分辨和定位目标函数。则

(11)

将式(11)对S求导并置为零，可得

(12)

综合式(11)、(12)，可得新的目标函数

(13)

基于LS准则的过采样点目标联合亚像元分辨和定位方法可表示为

(14)

式中：θ为待估计参数；xi，yi分别为第i个目标的x、y向位置。获得θ估计后，用式(12)即可实现目标灰度估计。在重心法求解中，也用式(12)估计目标灰度。

式(14)为高维非线性目标函数的优化问题。传统方法如高斯牛顿、最陡下降法等, 存在对初始估计值敏感、易陷入局部最优值、运算量大等问题。为此，引入QPSO算法实现式(14)的参数估计。

3.2 基于QPSO的目标函数最优化求解方法

粒子群优化(PSO)算法是一种仿生群智能计算技术[10-11]。PSO模拟鸟群觅食过程，通过群体中个体间的信息交流共享、合作竞争产生的群智能指导优化搜索过程，为全局最优算法，对初始估计位置不敏感[10]。但标准PSO算法仍存在收敛速度慢、陷入局部最优的缺点。为解决式(14)非线性目标函数优化问题，引入QPSO方法，该方法控制参数少，更利于高维复杂问题的求解。

QPSO以DELTA势阱为基础，认为粒子具有量子行为，使粒子能在整个量子空间的可行解进行搜索，全局搜索性能更优。QPSO利用波函数描述粒子状态，通过求解薛定谔方程得到粒子在空间某点出现的概率密度函数，并通过蒙特卡罗随机模拟方法得到粒子的位置方程[10-11]。

QPSO的粒子位置迭代计算为

(15)

(16)

(17)

(18)

式中：X为粒子；u为[0，1]间随机数；a为[0，1]间随机数；Pi，PG分别为粒子和种群最优位置；β为收缩扩张系数；M，D分别为粒子的数目和维数。

综合式(15)～(18)，可得第(k+1)次迭代时粒子的位置更新方程为

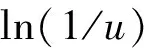
(19)

由式(14)，用QPSO实现过采样点目标像平面亚像元定位和灰度估计。假设CSO包含Nt个目标，则粒子搜索空间为2×Nt维，用式(13)计算粒子的拟合度。

基于LS-QPSO的参数估计流程包括以下步骤。

步骤a)设置问题的参数空间、粒子群规模M和粒子维数D，在参数空间内随机初始化粒子群。

步骤b)迭代搜索：用式(13)计算粒子的拟合度，并比较求出Pi，PG；用式(16)计算P；用式(18)计算mbest；用式(19)更新每个粒子的位置。

步骤c)判断收敛条件，若条件满足则输出估计结果，否则重复步骤b)。

步骤d)用式(12)估计目标灰度值。

3.3 对多个邻近点目标的分辨方法

上述分析中假定目标数已知，但实际应用中，存在多个邻近目标在过采样扫描图像中互相交叠情况，重心法无法分辨多个目标。为此，对LS-QPSO方法进行拓展。

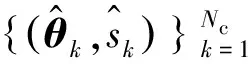
(20)

0.5kdln(UV)

(21)

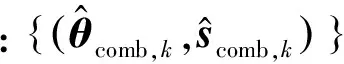
4 仿真试验

4.1 仿真参数

探测器按图1过采样方式设置：两排线列探测器并列，线列方向错开半个像元长度，扫描方向采样间隔为IFOV的一半。取QPSO算法的粒子总数为30。

4.2 单目标亚像元定位和灰度估计

针对单目标，分别在不同SNR，EOD，IFOV条件下，对比重心法和LS-QPSO方法的目标像平面定位和灰度估计性能。

4.2.1 不同SNR的仿真结果

探测器IFOV为90 μrad×90 μrad，取光学系统的EOD为0.6。不同SNR下，仿真所得两种方法的像平面定位和灰度估计结果分别如图2、3所示。其中：RMSE，NRMSE分别为定位精度均方根误差和灰度估计归一化均方误差；LOS为扫描相机指向目标的视线[14-15]。

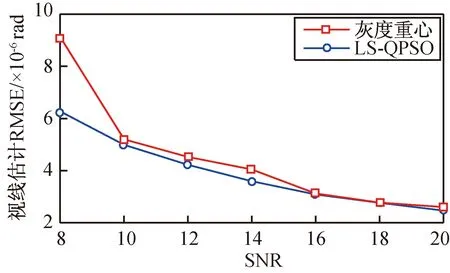
图2 不同SNR下目标定位精度Fig.2 Positioning accuracy for different SNR

图3 不同SNR下灰度估计精度Fig.3 Estimation accuracy of gray value for different SNR

由图2、3可知：两种方法均实现了对点目标的像平面亚像元定位，在SNR为8时，定位精度均优于1/9像元；随着SNR的提高，两种方法的定位精度和灰度估计精度均有提高；LS-QPSO方法的定位精度和灰度估计精度均优于重心法。

4.2.2 不同EOD的仿真结果

探测器IFOV为90 μrad×90 μrad，系统SNR取值12。在不同EOD下，仿真所得两种方法的像平面定位和灰度估计结果分别如图4、5所示。

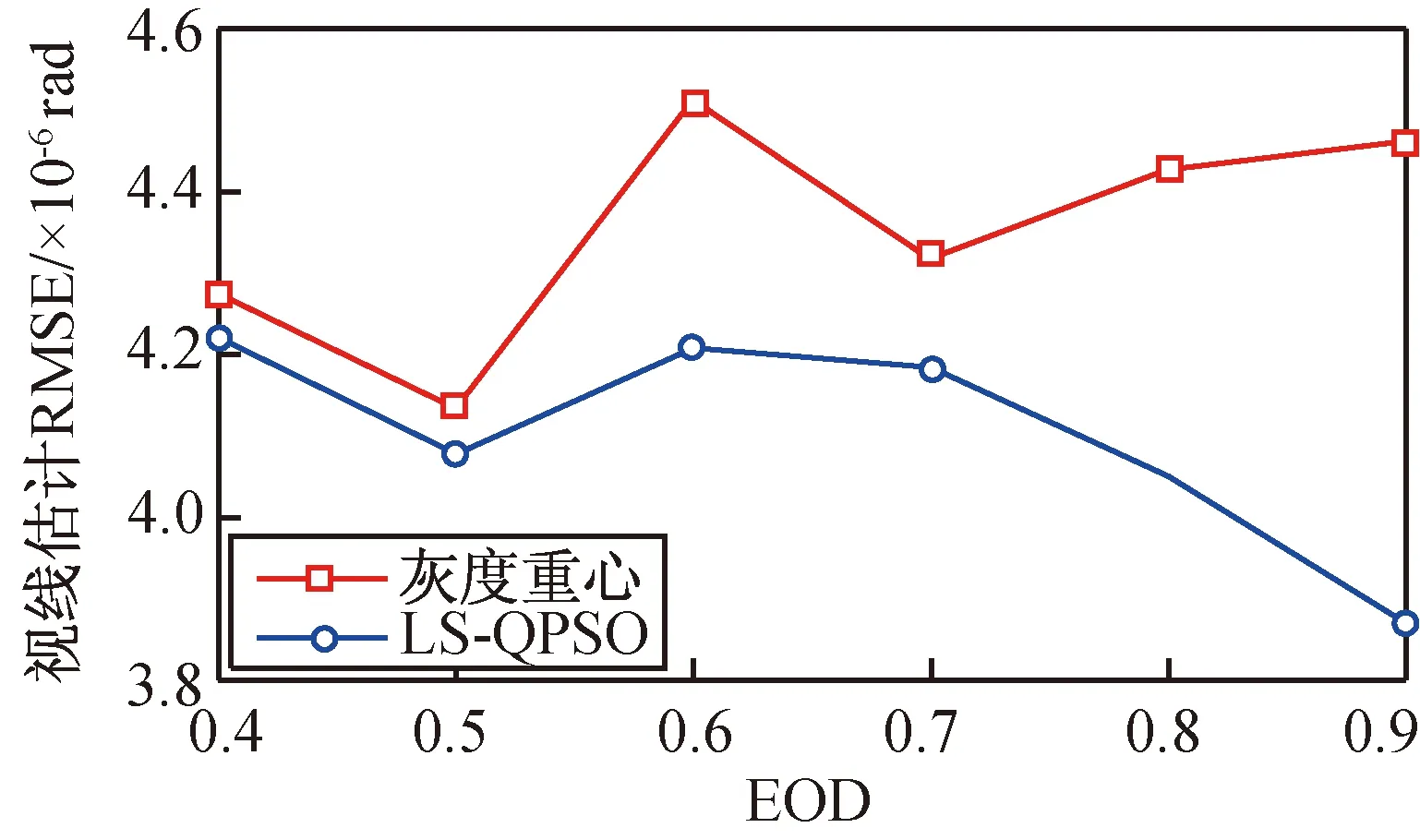
图4 不同EOD下目标定位精度Fig.4 Positioning accuracy for different EOD

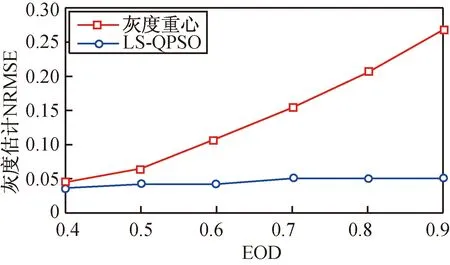
图5 不同EOD下灰度估计精度Fig.5 Estimation accuracy of gray value for different EOD

由图4、5可知：随着EOD的提高，重心法的定位精度和灰度估计精度均有所降低，这是因为EOD越高，目标能量扩散范围越小，重心法能利用的目标能量捕获像元数少，导致定位和灰度估计精度降低，但LS-QPSO方法的定位精度随EOD提高而提高，灰度估计精度则基本保持不变。显然，LS-QPSO方法的定位精度和灰度估计精度均优于重心法。

4.2.3 不同IFOV的仿真结果

取EOD为0.6，系统SNR为12。在30 μrad×30 μrad，50 μrad×50 μrad，70 μrad×70 μrad，90 μrad×90 μrad，110 μrad×110 μrad不同探测器瞬时视场下，仿真所得两种方法的像平面定位和灰度估计结果分别如图6、7所示。

图6 不同IFOV下目标定位精度Fig.6 Positioning accuracy for different IFOV

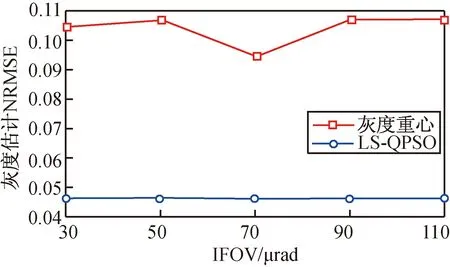
图7 不同IFOV下灰度估计精度Fig.7 Estimation accuracy of gray value for different IFOV

由6、7可知：随着像元IFOV的扩大，两种方法的目标定位精度均降低，LS-QPSO定位精度略优于重心法；灰度估计精度基本保持不变，LS-QPSO精度优于重心法。

4.3 邻近多目标分辨与定位仿真结果与分析

针对多目标情况，以2个邻近目标的分辨和定位仿真实例，给出基于BIC定阶准则的LS-QPSO联合目标个数、定位和灰度估计结果。

设探测器IFOV为90 μrad×90 μrad，取EOD为0.6。取两个目标，间隔102 μrad，目标灰度值分别为0.8，1.1。仿真所得探测器对两个目标的过采样成像效果如图8所示。由图8可知：因两个目标间距小，在过采样图像中呈现非规则状的大亮斑，重心法无法分辨两个目标。

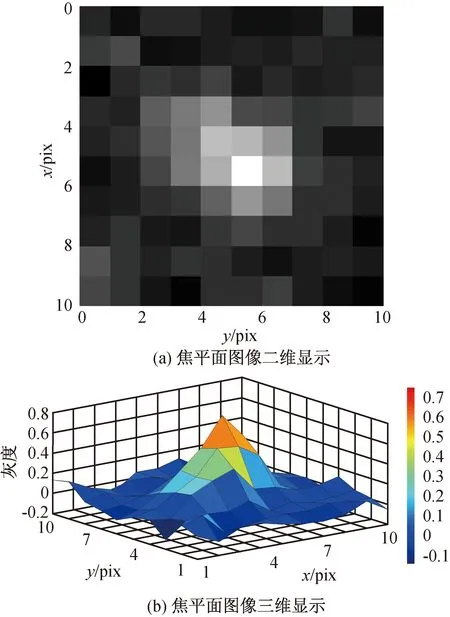
图8 两个邻近目标情况下的过采样成像仿真图Fig.8 Simulation image for two closely spaced objects

采用BIC准则的LS-QPSO方法，针对上述场景，进行100次Monte-Carlo仿真。每次仿真中两个目标的SNR在10～20间任意取值。统计100次Monte-Carlo仿真结果：对像斑目标个数的正确分辨率为96%，对两个目标的定位和灰度估计结果见表1。

表1 LS-QPSO对邻近多目标的分辨仿真结果

由此可知：基于BIC准则的LS-QPSO方法能有效实现对邻近多目标的分辨，并具备对各目标的像平面亚像元定位和高精度灰度估计。

5 结论

本文分析了红外扫描过采样体制对点目标的成像特点，认为过采样体制具备对点目标的像平面亚像元定位和灰度估计能力，利于进一步提升IRST系统对点目标的测向精度。现有关于红外扫描过采样的相关文献侧重于研究过采样的点目标检测性能分析与仿真。为此，研究了两种针对单个点目标的过采样亚像元定位和灰度估计方法，并根据实际应用情况对LS-QPSO方法进行拓展，使其具备对邻近多目标的分辨能力。仿真结果验证了过采样体制具备对点目标的亚像元定位和灰度估计能力，同时表明：对单个点目标，两种方法均能实现对目标的亚像元定位和高精度灰度估计能力，LS-QPSO性能略优；对邻近多目标，拓展后的LS-QPSO具对邻近多目标的分辨能力。提出的两种方法可为工程应用提供参考。后续将综合考虑实际成像链路影响因素，结合目标检测处理，进一步验证过采样体制的点目标亚像元定位和灰度提取的工程应用可行性。

[1] LATRY C, ROUGE B. The flight commissioning of SPOT5: the quincunx sampling mode[J]. Proceedings of SPIE, 2003, 4881: 189-199.

[2] LOMHEIM T S, MILNE E L, KWOK J D, et al. Performance/sizing relationships for a short-wave/mid-wave infrared scanning point-source detection space sensor[C]// Proceedings of IEEE Aerospace Conference. [S. l.]: IEEE, 1999: 113-138.

[3] 林两魁, 王少游, 王铁兵. 红外扫描过采样系统点目标检测性能分析与仿真[J]. 光学学报, 2016, 5(36): 0528001.

[4] 董玉翠, 苏晓锋, 林剑春, 等. 时空过采样探测系统性能仿真[J]. 强激光与粒子束, 2013, 25(3): 565-568.

[5] 饶鹏, 王成良, 胡胜敏, 等. 常规采样与过采样点目标检测性能比较分析[J]. 红外, 2013, 34(8): 6-10.

[6] LAWRIE D G, LOMHEIM T S. Advanced electro-optical space-based systems for missile surveillance[R]. Aerospace Report, TR-2001(8556)-1, 2011.

[7] 王世涛, 张伟, 金丽花, 等. 基于时-空过采样系统的点目标检测性能分析[J]. 红外与毫米波学报, 2013, 32(1): 68-72.

[8] 李静, 李为民, 陈晓东, 等. 重心法在光电信号处理中的应用[J]. 光学技术, 1999, 3(2): 57-59.

[9] 李中伟, 王从军, 史玉升. 一种结合梯度锐化和重心法的光条重心提取算法[J]. 中国图象图形学报, 2008, 13(1): 64-68.

[10] SUN W, XU B. A global search strategy of quantum-behaved particle swarm optimization[C]// IEEE Conference on Cybernetics and Intelligent Systems. Singapore: IEEE, 2004: 111-116.

[11] SUN J, FENG B, XU W. Particle swarm optimization with particles having quantum behavior[C]// IEEE Congress on Evolutionary Computation. Portland: IEEE, 2004: 325-331.

[12] IRIZARRY R A. Information and posterior probability criteria for model selection in local likelihood estimation[J]. J American Statistical Association, 2001, 96(453): 303-315.

[13] 周世椿. 高级红外光电工程导论[M]. 北京: 科学出版社, 2014.

[14] 林两魁. 天基红外传感器对中段弹道目标群的跟踪与超分辨技术研究[D]. 长沙: 国防科学技术大学, 2011.

[15] 张慧, 徐晖, 林两魁. 基于稀疏重构的空间邻近目标红外单帧图像超分辨方法[J]. 光学学报, 2013, 33(4): 0411001.

Research on Sub-Pixel Mapping and Intensity Extraction of Point Target via Infrared Scanning Over-Sampling System

LIN Liang-kui, WANG Shao-you, REN Bing-wen

(Shanghai Institute of Satellite Engineering, Shanghai 201100, China)

To improve precision of direction finding, the method of sub-pixel mapping and intensity extraction of remote point target via infrared scanning over-sampling system was studied in this paper. According to the characteristics of over-sampling image for remote objects, two methods of sub-pixel mapping for point target were studied, which were based on center of gravity and least square-quantum-behaved particle swarm optimization (LS-QPSO) respectively. The first one directly calculates the gray-weighted gravity center of over-sampling pixel-cluster from spot target, while the latter utilizes the least-square (LS) criterion, where an objective function for object’s sub-pixel position and amplitude estimation is established. Considering the high dimension and non-linearity of the function, quantum-behaved particle swarm optimization is adopted to realize the optimization of the objective function and to extract the state of the point target. Further, the LS-QPSO method is improved to resolve multiple closely spaced objects. Results show that both methods can effectively realize sub-pixel mapping for point target, and the LS-QPSO obtains slightly better performance. The LS-QPSO can further realize resolution of closely spaced objects on the oversampling scanning image meanwhile.

point target; scanning over-sampling; sub-pixel mapping; intensity estimation; least square; quantum-behaved particle swarm optimization; center of gravity; closely spaced objects

1006-1630(2017)03-0033-07

2016-10-11；

2016-11-28

国家自然科学基金资助(61401474)

林两魁(1980—)，男，博士，主要研究方向为光学载荷设计与分析、红外目标检测、多传感器多目标跟踪、信息融合和机器学习等。

TP75

A

10.19328/j.cnki.1006-1630.2017.03.004