基于中位数GARCH模型的汇率波动率预测

张曼，赵学靖，田人合

（1.兰州大学数学与统计学院,兰州730000；2.中国科学院成都文献情报中心，成都610041；3.中国科学院大学，北京100049）

基于中位数GARCH模型的汇率波动率预测

张曼1，赵学靖1，田人合2,3

（1.兰州大学数学与统计学院,兰州730000；2.中国科学院成都文献情报中心，成都610041；3.中国科学院大学，北京100049）

自2005年7月21日汇率改革以来，人民币汇率的波动性发生了根本的变化。汇率波动越来越频繁、越来越大。汇率的准确预测无论是对国内还是对国际都有着至关重要的意义。文章预测汇率收益率的波动性，在ARCH和GARCH模型的基础上提出了中位数GARCH模型，并采用人民币兑美元的数据来检验模型的有效性。由预测误差可以看出，中位数GARCH能很好地减小预测误差。

中位数GARCH模型；GARCH；波动率预测

0 引言

汇率是两种货币的折算的一个比率数字，它是衡量一国货币价值的重要指标。随着社会的发展和金融的全球化，资金在国际和地区间的流动变得越来越频繁。它不仅影响到国内的经济，也在国际间的货币收支上起着不可或缺的作用。因此汇率在金融市场的波动性已经成为了现代金融理论和金融研究的一个重要课题。汇率的波动带来的风险的变化，大的汇率波动往往带来的风险较大；相反，小的波动带来的风险较小。我国2005年7月21日对汇率进行了调整，汇率不再是单一的盯住美元，政府放松了对汇率的监管，波动越来越频繁，幅度也越来越大。汇率改革以来，人民币的累计升值幅度已达25%左右，汇率的不断变化吸引了部分学者来进行研究其特性。

汇率作为一种金融数据同样具有非正态、非平稳、异方差的特性，这些特性的存在使得传统的最小二乘方法极有可能带来“伪回归”的结果。针对金融数据的这一特性Engel(1982)提出了自回归条件异方差(ARCH)模型[1]。Hsieh曾经证明了ARCH能够用来描绘汇率波动的情况[2]。

在ARCH模型的基础上发展了GARCH族模型[3]。凯恩克(Koenker)和巴西特(Bassett)于1978年提出的分位数回模型[4]，分位数回归对数据没有太大的要求。

分位数回归能够适应数据尖峰、厚尾或者显著异方差的特性，分位数回归在数据非正态的情况下稳健性要优于最小二乘回归。它是凯恩克(Koenker)和巴西特(Bassett)于1978年提出的[5]。分位数回归(QR)利用解释变量和因变量的条件分位数进行建模。与普通的最小二乘回归(OLS)相比，它能够提供更加充分的模型[5]。

分位数回归中每一个分位数的估计都是基于整体样本的加权来完成的，现在分位数回归已经被应用到许多领域来解释各种问题。例如工资问题、生存分析、财务分析、经济研究、环境研究、互联网和通信技术、医疗保健支出、小型企业经营业绩等[6-9]。本文溢出中位数GARCH模型，研究汇率波动性即期预测。

1 相关理论基础

1.1 ARCH模型

ARCH(q)模型在形式上是一个回归模型，其条件波动率（也成为条件方差）是因变量，往期收益率平方值是自变量。ARCH(q)模型假设收益率序列{} rt由下式生成：

其中：αi，i=1，...，q和w是未知参数，，并且εt和rt-j，j=1，2，......是相互独立的。下标里的t-1表示以t-1时刻之前的收益率做为条件计算第t期收益率的方差。因为εt被假定为具有单位方差，因此的方差等于。这里可以看出：序列的方差是随着时间变化的，体现出了异方差性。

RCH(q)的第二个式子表明，这个随着时间变化的条件方差是序列的滞后有限项的二次方的线性组合。

1.2 GARCH模型

当ARCH(q)中的q比较大时，可以在ARCH模型第二个式子中加入过去的条件方差项，这样就得到了广义自回归条件异方差模型(GARCH)。对于序列，如果：

这就是Bollerslev(1986)和Taylor(1986)提出的GARCH (p,q)的模型。式（3）中和βj，j=1，...，p是未知的参数，，并且εt和rt-m，m=1，2，......是相互独立的。GARCH(p,q)模型形式上是一种是用滞后q阶的的平方和滞后p阶条件方差来预测将来变化的时间序列建模方法。已经有很多文献证明这些模型的预测效果要比同方差的方法要好很多[10-12]。

1.3 分位数回归

式（4）τ表示分位数，τ的取值可以是(0,1)之间的任意小数，给定τ就说明在建模的过程中位于拟合线之下的数据比例为τ。当分位数为0.5时，分位数GARCH就是中位数GARCH模型。

分位数在系数估计上与OLS回归存在明显的差别。OLS的估计系数用的是最小二乘法，分位数回归系数估计用的是加权最小一乘法，他们的目标函数分别为：

1.4 变量选择准则

Brooks和Burke提出了用信息准则(如AIC,BIC,AICC等)来确定GARCH模型中的p和q[13]。本文模型选择的时候用AIC信息准则。

AIC是由日本的统计学家赤池（Akaike）1973年提出的[14]。AIC准则趋向于选择使AIC=-2log(L)+2k最小的模型。其中L是极大似然估计，-2log(L)表示模型的精确度，k为参数的数量表示模型的复杂度。

2 实证分析

本文数据来自国家外汇管理局官方网站(http：//www. safe.gov.cn/)，这里选用的是人民币兑美元的数据，所有的数据均是人民币汇率买卖双方中间价。这里选取了2011年5月25日至2015年8月10日，从2011年5月25日以后汇率数据就稳定在了6.5以下，本文研究的是汇率在稳定在6.5以下的数据。

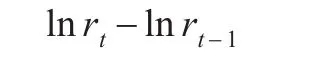
所以本文以价格对数的差分表示收益率。收益率基本统计性质如表1所示。

表1 数据统计量

表1表示的数据各个统计量的表格，由表1可以看出均值和中位数几乎为0，中位数大于均值，数据是左偏的，这也可以由skewness小于0看出。JB统计量显示这组数据是非正态的，ADF统计量的p值较小为0.01在置信度为5%的水平下，认为数据是平稳的；而第四行的最后一个数据反应的是原始数据的ADF统计量，但是这个ADF的p值为0.4892，认为原始数据是不平稳的，比较两个ADF值可以看出一阶差分能够消除数据的不平稳性。

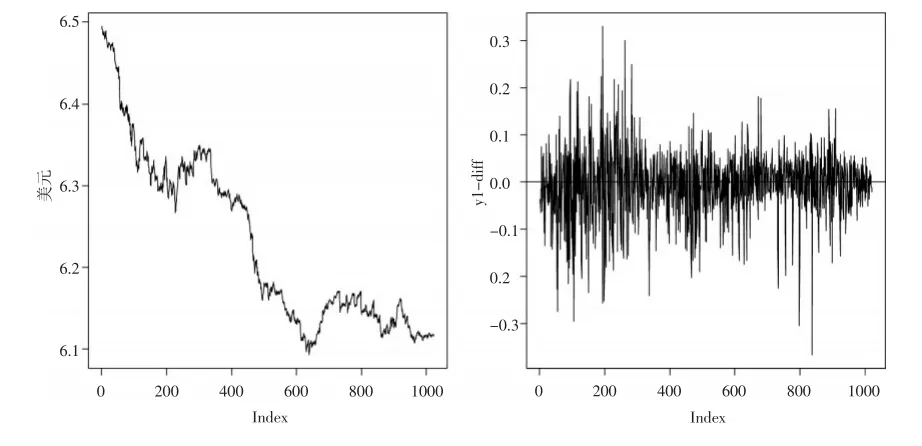
图1 汇率收益率趋势图

图1是数据的趋势图，左边的图是原始数据的趋势图，可见所选的美元兑人民币的汇率数据在所选区间内是呈下降趋势的，这说明我国的货币是不断升值的。右图是收益率趋势图，没有明显的增长或减小的趋势，但是能看出波动集群性，这直观表明了异方差的存在。

异方差的存在说明有ARCH效应，ARCH效应检验用的是McLeod.Li方法，原假设为H0:σ1=σ2=...=σn，由R语言rugarch包里面的McLeod.Li.test的检验结果可以明显看出是否有异方差如图2所示。

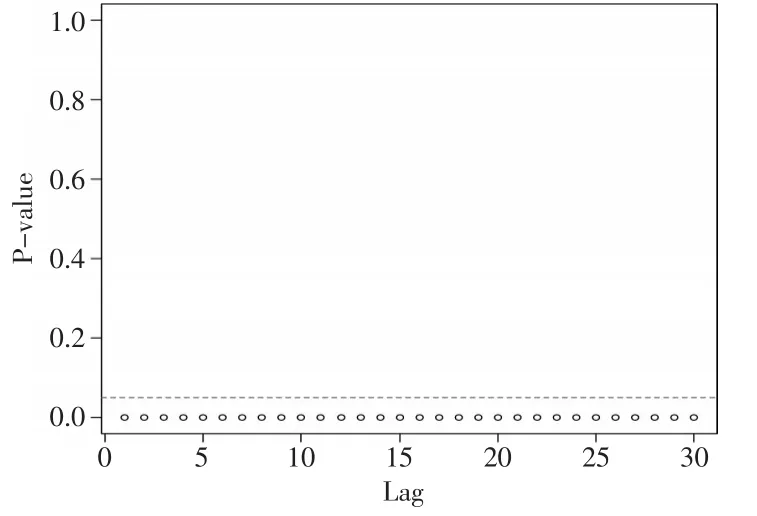
图2 ARCH效应检验的McLeod.Li.test结果显示图

其中横轴表示滞后阶数，纵轴表示McLeod.Li检验的p值，虚线表示p值为0.05。由图2可以看出在滞后1～30阶的情况下ARCH效应都是明显的，滞后阶数比较大时仍具有ARCH效应，所以考虑应用GARCH模型。

在GARCH模型中有p,q需要选择，这里应用的是AIC。同时，为了保持一致性MRGARCH中p,q的选择方法也用AIC，选择结果见表2所示。

表2 选择GARCH(p,q)中p,q的结果

表2中前三列是中位数GARCH模型选择的过程，后三列是GARCH模型的选择过程。前三列可以看出：选择分位数中位数GARCH(0,1)比较合适，这时模型的解释变量只有滞后一期的条件方差，同时模型中的系数通过检验，比较显著。后三列的结果显示选择GARCH(1,1)比较合适，这也验证了很多文献中提到的一般选取GARCH(1,1)的说法[15]。

由此可以得到两种方法下最优的模型MGARCH(0,1)和GARCH(1，1)，为了检验模型的优劣，下面进行一个预测相对误差的比较，这里进行的是一步向前预测，共预测了一周的数据(5期)。需要注意的是每次预测是都需要对模型进行选择，从而得到比较准确的预测效果。训练数据共1015个，得到的预测结果见表3所示。

表3 预测结果及预测误差（窗宽1015）

表3第一列表示中位数GARCH对条件方差的预测结果，第二列表示GARCH模型对条件方差的预测结果。第三列是真实值，第四列和第五列是对预测效果的一个直观的体现，用的是预测误差。由预测误差可以看出：分位数GARCH模型的条件方差的预测效果要比GARCH的效果要好的多，这一结论在第四和第五列体现的较为直接。GARCH的预测误差在10%左右，而中位数GARCH的预测误差在0.2%～0.3%之间徘徊。在预测的这五期数据里面，每一期的MRGARCH的预测效果都要比GARCH模型的效果要好很多。

3 结论

在进行波动率预测时，用中位数GARCH模型要比一般的GARCH模型的预测结果要精确，这对进一步的收益率预测和定价的精确预测带来了一定的优势。波动率体现金融市场质量和效率，因此准确预测是非常重要的。波动率的准确预测能够给投资者一定的投资依据，能够对我国的汇率政策的制定带来一定的理论依据。

[1]Engle R F.Autoregressive Conditional Heteroskedasticity With Estimates of the Variance for U.K.Inflation[J].Econometrica,1982,50, (4).

[2]Bollerslev T.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometrics,1986,31,(3).

[3]Koenker,Bassett.Regression Quantiles[J].Econometrica,1978,46,(1). [4]Hsieh D A.Testing for Nonlinear Dependence in Daily Foreign Exchange Rates[J].Journal of Business&Economic Statistics,1989,62, (3).

[5]Yu K,Lu Z,Stander J.Quantile Regression:Applications and Current Research Areas[J].The Statistician,2003,52,(3).

[6]Machado J A F,Mata J.Counterfactual Decomposition of Changes in Wage Distributions Using Quantile Regression[J].Journal of Applied Econometrics,2005,20,(4).

[7]Wang D H M,Yu T H K,Liu H Q.Heterogeneous Effect of High-tech Industrial R&D Spending on Economic Growth[J].Journal of Business Research,2013,66,(10).

[8]Yu T H K,Wang D H M,Chang L Y.Examining the Eterogeneous Effect of Healthcare Expenditure Determinants[J].International Journal of Behavioural and Healthcare Research,2011,2,(3).

[9]Seo J H,Perry V G,Tomczyk D,et al.Who Benefits Most?The Effectsof Managerial Assistance on High-Versus Low-performing Small Businesses[J].Journal of business Research,2014,67,(1).

[10]Day T E,Lewis C M.Stock Market Volatility and the Information Content of Stock Index Options[J].Journal of Econometrics,1992,52, (1).

[11]Aguilar J,Nydahl S.Central Bank Intervention and Exchange Rates: the Case of Sweden[J].Journal of International Financial Markets, Institutions and Money,2000,10.

[12]伍戈,姜波克,唐建伟.外汇市场信息与汇率波动性研究[J].财经研究,2002,28(7).

[13]Brooks C,Burke S P.Forecasting Exchange Rate Volatility Using Conditional Variance Models Selected by Information Criteria[J]. Economical Letters,1998,61,(3).

[14]Akaike H.Maximum Likelihood Identification of Gaussian Auto-regression Moving-average Models[J].Biometrika,1973,(60).

[15]殷微波,王峰.人民币汇率预测——基于GARCH模型[J].当代经济,2007,(8).

（责任编辑/浩天）

O213.9

A

1002-6487（2017）11-0073-03

国家自然科学基金资助项目（11301237）；教育部留学回国人员科研启动基金资助项目（第44批）；兰州大学中央高校基金资助项目（lzujbky-2015-80；lzujbky-2013-178；lzujbky-2012-15）

张曼（1989—），女，山东菏泽人，硕士，研究方向：高维数据统计分析。田人合（1988—），男，甘肃陇西人，博士研究生，研究方向：情报研究方法与技术、数据科学。