多元线性回归计算矿石体重方法的优化——以某铜锌矿为例
2017-07-05严利伟王昌南唐高林刘琪
严利伟,王昌南,唐高林,刘琪
多元线性回归计算矿石体重方法的优化——以某铜锌矿为例
严利伟,王昌南,唐高林,刘琪
(四川金伯利地质勘查有限公司,成都 610091)
本文提出多元线性回归计算矿石体重的优化方法,并以某铜锌矿为例,采用优化方法计算出体重值与矿石品位之间的方程关系。结果表明,铜锌矿的矿石体重与铜(Cu)、硫(Sp)品位之间线性关系明显,线性方程的拟合效果极好。预测体重与实际体重之间平均误差<5%,可以直接利用于实际生产。
矿石体重;矿石品位;多元线性回归;优化
矿石体重是矿床勘查开发过程的一项重要参数,获得准确的体重估值是矿床资源量估算的前提条件。传统上矿石体重值是通过小样本抽样求算术平均值或者根据体积或重量进行加权平均求得。但受样本大小局限,并且由于取样方式的随机性,求得的矿石体重往往与理想的矿石体重存在较大偏差。近年来,许多学者尝试建立小体重与矿石品位之间的线性方程,直接通过矿石品位推算矿石体重值,取得了一定的效果,但实际操作中存在以下问题:①没有排除不同元素品位之间可能存在的自相关性;②默认矿石体重和品位之间直接线性相关,没有建立模型加以验证;③对线性方程的拟合优度以及自变量显著性缺乏统一的评判标准。以上问题直接影响线性方程式的准确建立,从而影响估值结果的准确性。为此,本文以川西南某铜锌硫化物矿床为例,重点结合上述三个问题,对多元线性回归计算矿石体重的方法进行优化。
1 体重多元线性回归的优化途径
1.1 元素品位之间自相关性的排除
由于矿石中矿物组合的多样性,元素品位之间往往并非相互独立不相关联。例如,当两种元素出现在同一种矿物中时,元素品位实际呈现出固定比例的关系。同时采用这两种元素品位参与回归,相当于重复引入自变量。当一种元素同时赋存于多种矿物中的时候,其品位实际可以通过这些矿物中其他元素进行计算得出,相当于这种元素品位与其他元素品位值之间存在已知的线性关系。线性回归模型中的自变量之间存在的精确相关关系或高度相关关系会使模型估计失真或难以估计准确。但由于矿石中矿物类型以及成矿元素的赋存状态往往是已知的,我们可以依据上述信息对自变量进行预筛选及预处理,确定或者分离出与体重相关且不存在已知自相关性的自变量,从而排除这种自相关性对线性方程拟合的影响。
1.2矿石体重与元素品位的线性关系的建立
矿石体重与元素品位之间的具体关系需要建立相对理想的模型来确定。冯适安[1]通过铅锌矿的理想模型构建了铅锌矿中铅、锌品位与矿石体重之间的方程式。在假定所有成矿元素均赋存于不同矿物中的前提下,这种方法可以推广应用到其他多金属矿床。方法如下:
假设脉石矿物比重为常数0,为矿石量,为矿石体积,vvv为各矿石矿物体积,ddd为各矿石矿物比重则有:
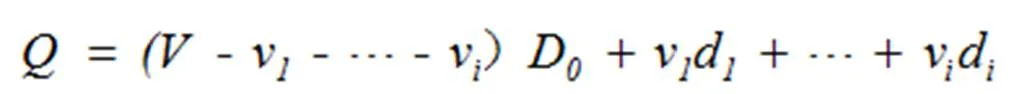
设ccc为各元素在所赋存的矿石矿物内的品位,PPP为各元素金属量为矿石体重,,xxx为各元素在矿石中的品位,kkk为常数,则有:
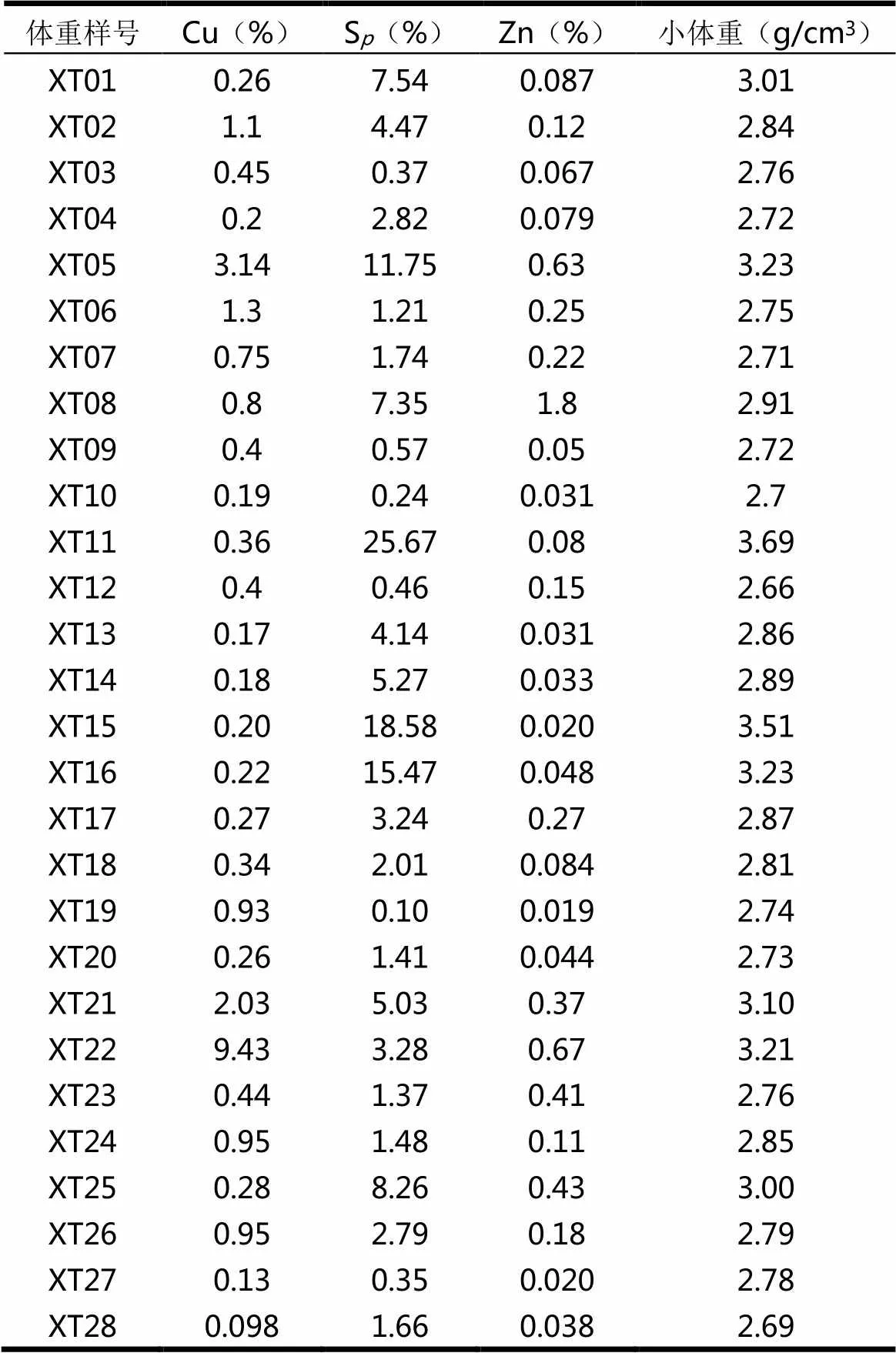
表1 某铜锌矿品位及小体重值
根据理论模型的推算表明,矿石体重的倒数与元素品位之间可能存在显著的相关关系。因此采用体重倒数,而不只是体重值作为因变量,可以获得更为准确的拟合方程。
1.3 线性方程拟合效果的分析方法
前人一般都是采用复相关系数R或者R2或来评判多元线性方程的拟合效果[2-3],R的绝对值越接近于1,说明拟合效果越好。为了验证因变量与自变量总体存在线性关系,拟合方程还必须通过显著性检验(F检验)。由于矿石体重值会直接应用于储量计算,因此在统计参数的评判之外还必须要考虑实际的应用效果。一般而言,体重值的误差远小于储量值的误差时才有较好的应用价值。结合生产实际情况,我们推荐预测体重与实际体重的平均误差应当控制在10%以内。
复相关系数只是对于模型拟合优度的考量,并非说明各个自变量对因变量的影响显著。在回归分析中,不仅要模型的拟合度高,还要得到总体回归系数的可靠估计量[4]。基于前述的模型,在矿石品位值较高的情况下,一般都可以认为其对体重值的影响较大,可以先作为自变量参与回归。少数元素品位较低,对体重影响较小,可以采用变量显著性检验(t检验)加以排除。这样可以确保包括所有可能影响体重的因素,同时排除了无关信息的干扰。
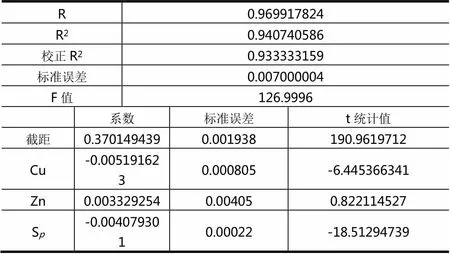
表2 Cu、Sp、Zn三个自变量多元线性回归统计量
2 优化方法建立回归方程实例
某铜锌矿围岩地层为古元古界里伍岩群,围岩岩性以石英岩、蚀变二云片岩为主。矿体呈似层状大致平行于片理产出,矿石矿物以黄铜矿、磁黄铁矿、闪锌矿为主,次为方铅矿、黄铁矿等,含量较少。脉石矿物主要为石英、黑云母、绢云母、绿泥石等。矿石多为浸染状、条带状、网团状构造,少量为块状构造。29块样品测定的体重值2.66~3.69(g/cm3),矿石品位分析主要成矿元素Cu、Zn、S三项,其中S品位0.45%~26.7%,Cu品位0.1%~9.43%,Zn品位0.02%~1.8%(表1)。样品均为致密块状岩石、孔隙度与湿度对体重影响较小,可不作考虑。
由于矿石中的成矿矿物主要为磁黄铁矿(Fe1-xS, x=0-0.17)、黄铜矿(CuFeS2)、闪锌矿(ZnS),其中Cu和Zn分别只赋存于黄铜矿和闪锌矿中,S同时赋存于三种矿物之中,与Cu、Zn均有一定相关性,因此需要在S品位中除去黄铜矿和闪锌矿中的S含量,以磁黄铁矿中的S(以S表示)作为一个自变量引入。
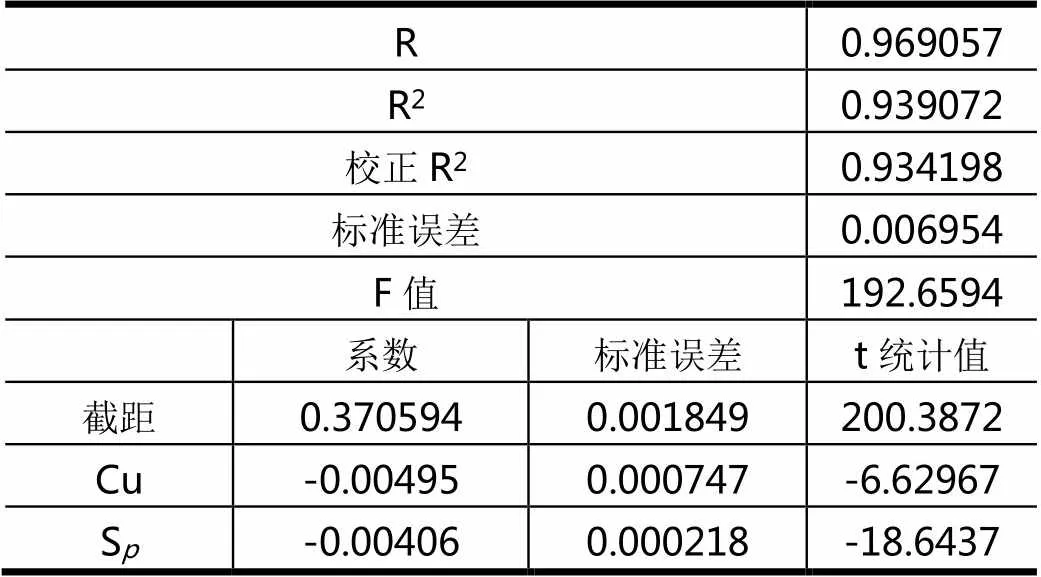
表3 Cu、Sp两个自变量多元线性回归统计量
本次多元线性回归采用EXCEL软件中加载的回归分析工具进行,以Cu、S、Zn三个自变量对体重倒数进行回归,得到以下统计结果:
由于回归统计值中复相关系数R值和R2分别为0.97和0.94,均接近于1,给定显著性水平0.05,F值>F0.025(3,24)=2.33,说明方程线性拟合的效果非常好。设计原假设H0:bi=0(i=1,2…k)与备择假设:H1:bi¹0,给定显著性水平a=0.05,查得相应临界值:t0.025(24)=2.064。包括常数项在内的3个自变量(截距、Cu、S)标准误差较小,且都在95%的水平下显著,都通过了变量显著性检验。Zn品位值的标准误差较大,且由于| t |< t0.025(24),接受原假设H0。因此我们认为Zn的品位值与体重之间没有关联,转而采用Cu、S两个自变量进行回归,回归结果见表3。
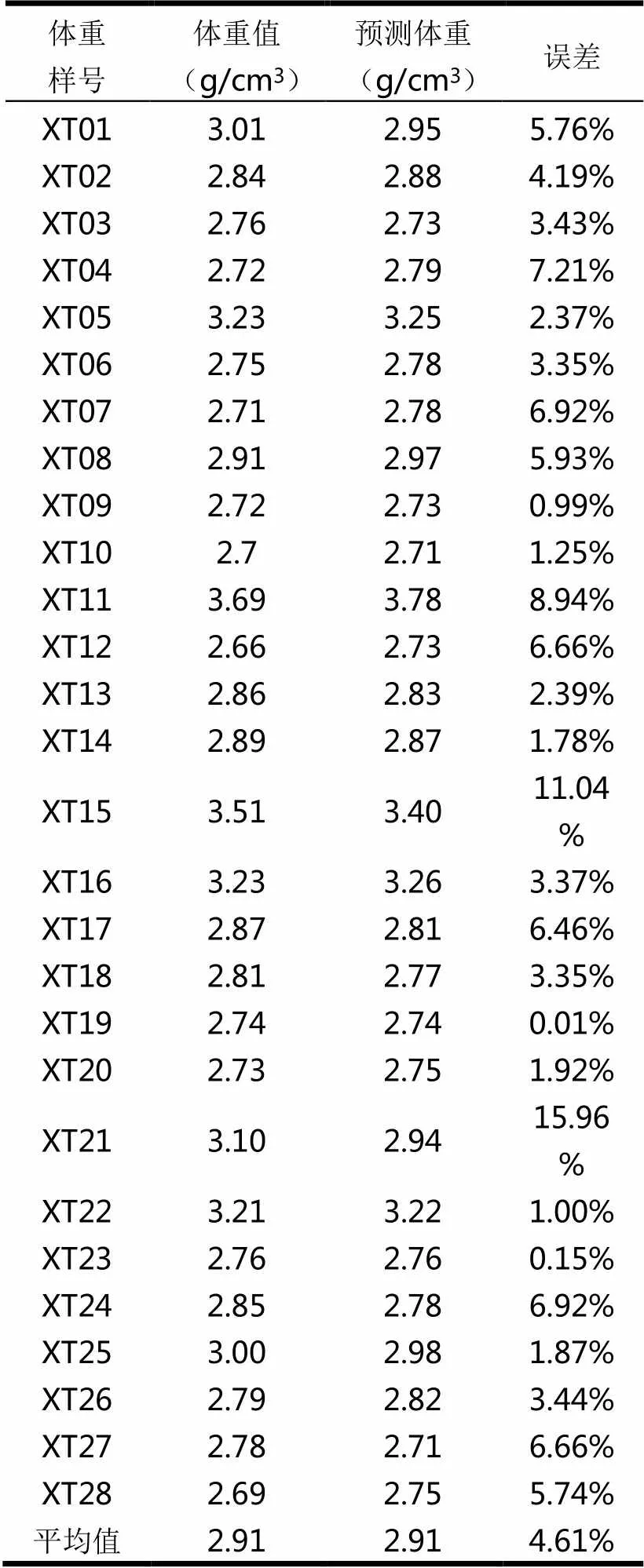
表4 预测体重与真实体重误差
给定显著性水平a=0.05,F>F0.025(2,25)=2.53,表明方程总体线性显著。包括常数项在内的3个自变量都通过了显著性检验。据上述参数,设y为体重值,拟合的方程为:y=1/(0.370594-0.00495Cu-0.00406S)。以0.00495Cu+0.00406S为x,体重倒数为y’,进行坐标投影(图1)。结果表明(表4),体重倒数与品位值呈现明显线性趋势。经统计,通过回归方程计算的预测体重与真实体重的误差大部分在8%以下,平均误差仅有4.61%,因此可以认为回归方程有较好的预测效果,可以直接用于储量计算中。
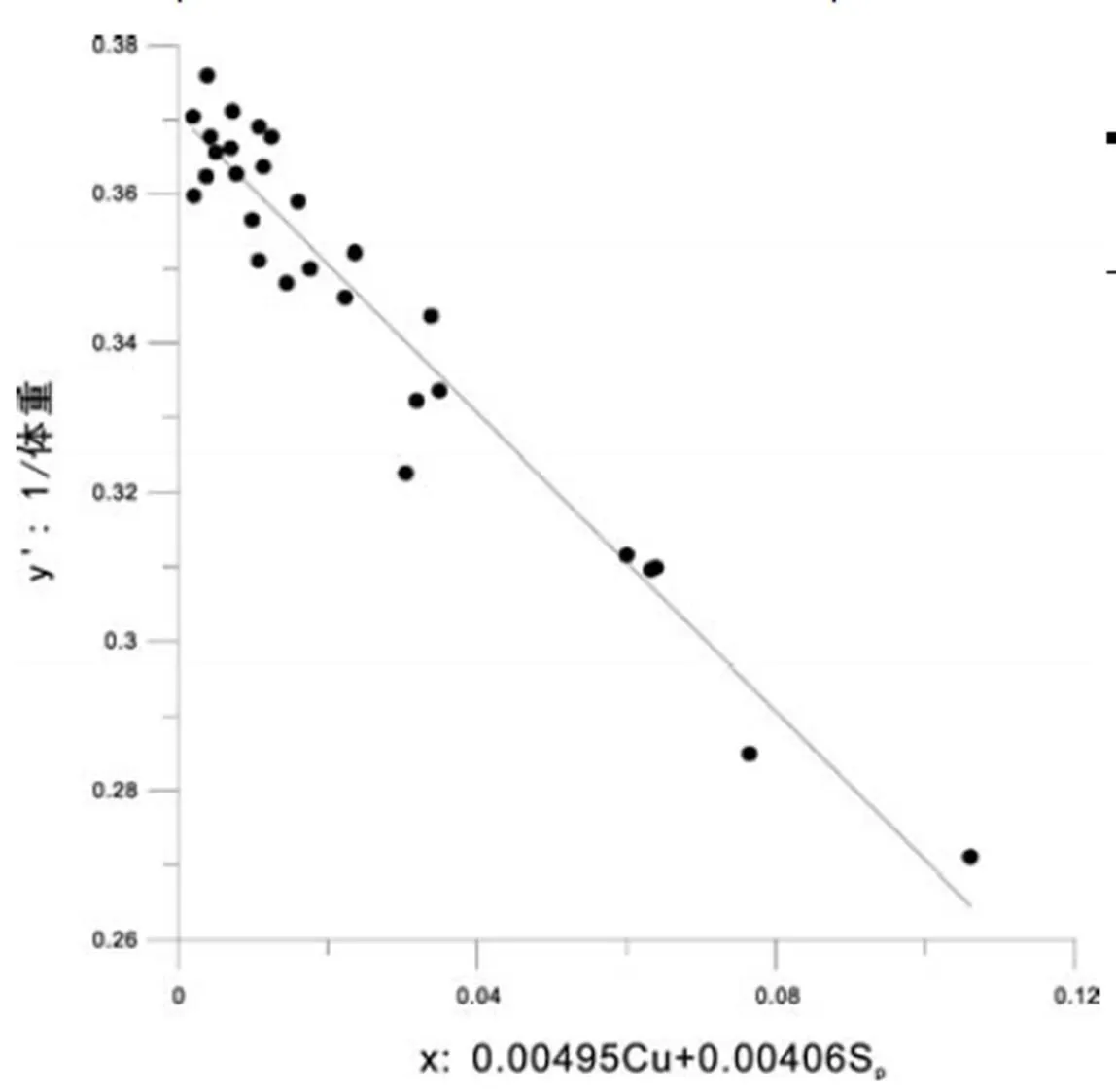
图1 体重倒数与品位之间线性关系
3 讨论
3.1回归分析的质量
本文采用的回归实例采用有限数据就获得了比较好的回归结果,主要是因为本例中矿石组成与理想的矿石模型比较接近。具体表现为矿石矿物种类较少,对体重影响较大,且脉石成分、比重比较稳定。在实际生产应用中可能会出现一些问题。例如对于某些比如低品位矿或者稀有金属矿,其元素品位与体重之间可能不存在相关性,回归方法可能并不适用。或者对体重影响较大的是一些非成矿元素,仅利用成矿元素品位,回归效果往往不佳。因此在应用之前需要对其可行性有基本的判断,同时通过增加样本数、优选自变量的方法提高回归方程的质量。
3.2 应用前景
矿石体重的多元线性回归方程实际上提供了采用品位值来预测体重值的最佳方法,在实际生产中的应用十分广泛。例如,通过回归方程计算体重与平均方法求得的矿石体重对比,可以及时发现小体重取样中存在的偏差。在储量计算方面,可以根据块段内矿石平均品位为各块段分别计算体重。同样,在基于矿体三维模型的储量计算中,也可以引入多元线性方程分别为矿块进行体重赋值。以上方法相当于对矿体不同部位的体重值进行量化赋值,更符合矿体的自然特征,可以极大提高储量计算的精度。
[1] 冯适安.1983.多金属矿床中矿石体重与金属品位的关系[J].湖南地质,2(2):58-61.
[2] 张景平,李社.2001. 基于SPSS的矿石小体重与品位的多元回归分析模型的构建[J].华东理工大学学报(自然科学版),34(1):62-66.
[3] 林喜.矿石体重的多元线性回归分析及其检验[J].福建地质,2009,29:157-163.
[4] 刘晓石,陈鸿建,何腊梅,等.概率论与数理统计(第二版) [M].北京:科学出版社,2005.
Optimization of Multiple Linear Regression Analysis of Ore Density — By the Example of a Cu-Zn Deposit
YAN Li-wei WANG Chang-nan TANG Gao-lin LIU Qi
(Sichuan Jinboli Geological Exploration Co., Ltd., Chengdu 610091)
This article puts forward an optimized method of calculating ore density by use of multivariate linear regression and by the example of a Cu-Zn deposit. The results show that ore density value has a clear linear relationship to the grades of copper(Cu) and sulfur(S). The average error between the predicted density and the measured density is less than 5%. Such method can be well adapted to production.
ore density; ore grade; multivariate linear regression
P628+.1;P618.41
A
1006-0995(2017)02-0331-04
10.3969/j.issn.1006-0995.2017.02.037
2016-06-26
严利伟(1986-),男,江苏南通市人,硕士,从事地质勘查工作
