基于时间序列分析法的滑坡变形特征研究

刘亚，蔡建华，董建辉



基于时间序列分析法的滑坡变形特征研究

刘亚1，蔡建华2，董建辉3

（1.中国建筑西南勘察设计研究院有限公司，成都 610052；2.中铁西南科学研究院有限公司成都 611731； 3.成都大学建筑与土木工程学院，成都 61010）

应用时间序列分析方法建立滑坡位移ARIMA预报模型。采用差分平稳，自回归AR模型和移动平均MA模型对滑坡位移进行预测，得到了该滑坡监测点TP1的预报模型为ARIMA（2,2,1），然后分析对比实测与预测位移–时间曲线之间的关系。计算结果能够较好地体现出滑坡在外界诱发因素作用下位移的发展变化趋势，说明所建滑坡位移预测预报模型效果较好，在滑坡位移预测中是有效可行的。

滑坡；位移预测；研究；白石乡；时间序列

随着学者对滑坡认识不断深入，滑坡监测及预报模型的研究[1-4]已成为滑坡研究中的重要方向之一。由于不同滑坡的工程地质结构、地形地貌、岩土体参数等不同，其变形规律也千差万别。同一滑坡的变形过程也受到多方面因素的影响，如环境条件的改变、多级滑面的形成等都会使滑坡的位移-时间曲线出现波动，从而造成滑坡动态分析的难度增加。因此，有必要建立一种能有效反映滑坡位移波动性特征及定量反映影响因素作用的分析模型[5-10]，使之能更加真实、精确，有助于提高滑坡预报精度。

该文通过对滑坡变形分析与预报进行了系统研究，应用时间序列的分析方法，建立差分自回归滑动平均模型（ARIMA）模型、剔除监测数据的噪声、检验模型的合理性，并且进行了临滑位移预测。

1 时间序列分析原理

时序分析认为同一变量在某时刻的观测值与该时刻之前历史数据相关联。因此，若[Dt] (t= 1 2… )是在时间上的无限延伸序列，则可以提出这样一种模型来描述该序列

通常假定ζt是均值为常数的正态白噪声，引入后移算子B，可得BDt=Dt-1，BkDt=Dt-k，Bζt=ζt-1，Bkζt=ζt-k，则式（1）可变为：

（2）

对于平稳时序可以建立AR(n)、MA(m)、ARMA(n,m)。通过a阶差分的ARMA(n,m)可以建立ARIMA(n,a,m)模型。

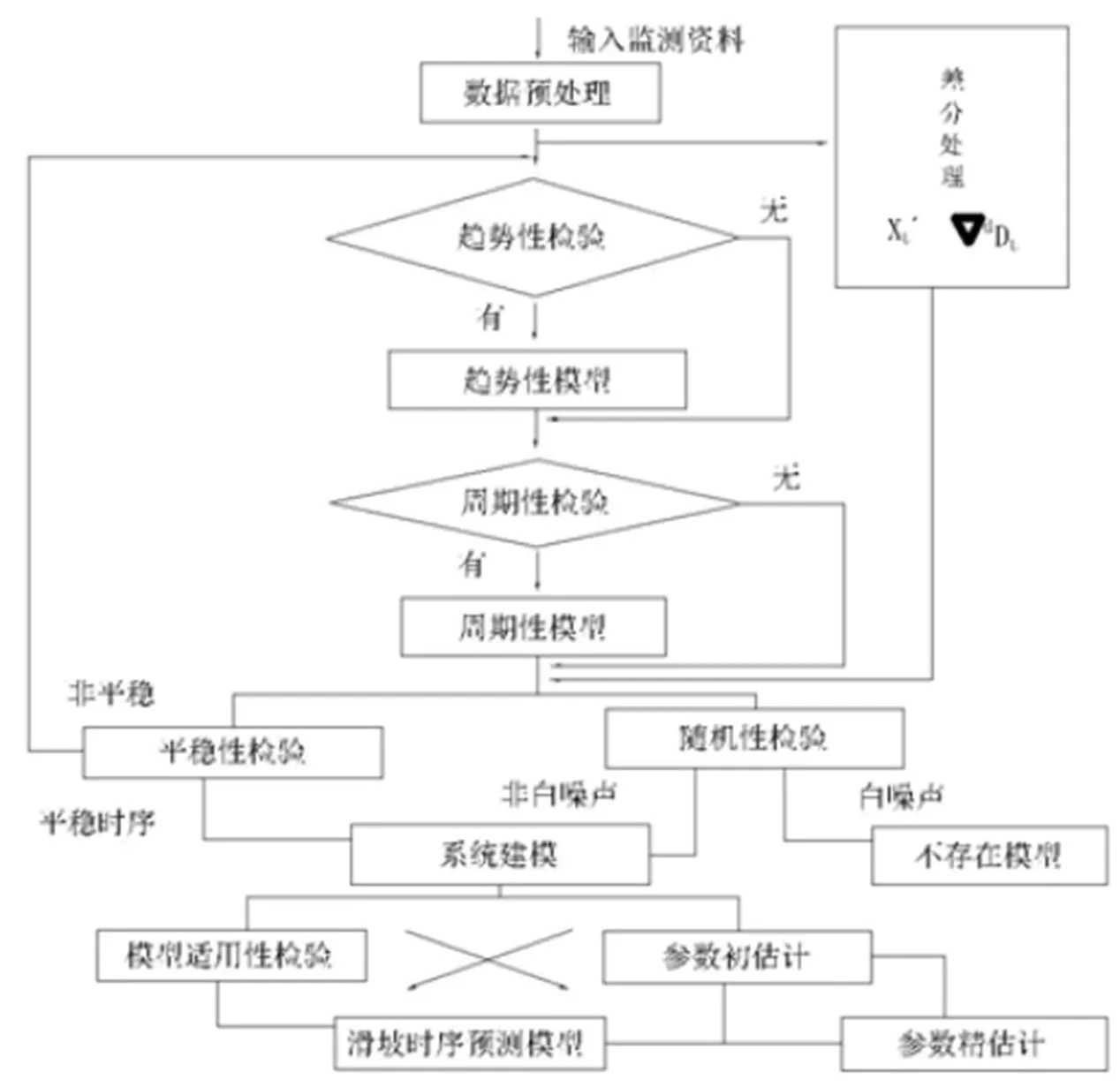
图1 时间序列建模过程图

滑坡在自然环境条件和人为因素的作用下产生变形一方面滑坡变形受其自身地质结构条件控制, 具有一定的规律性, 即变形表现为一定趋势性确定性的位移Xt,另一方面因其地质环境等因素不断变化, 使滑坡变形受多种因素干扰，呈现季节性周期波动的位移Yt, 还有随机干扰Nt，滑坡的位移时序可用(3) 式表示, 显然, 滑坡位移时序为非平稳时序, 必须对监测位移时序进行一系列的数据预处理, 直至获取平稳时序Lt,再借助于平稳时序建模理论。

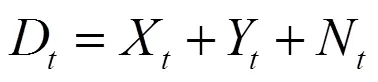
时序分析有以下特点：

1）运用时间序列分析要比相关分析法、周期图法等方法所获得的统计特性要精确,因为时序模型是动态模型,具有对动态数据的外延特性。

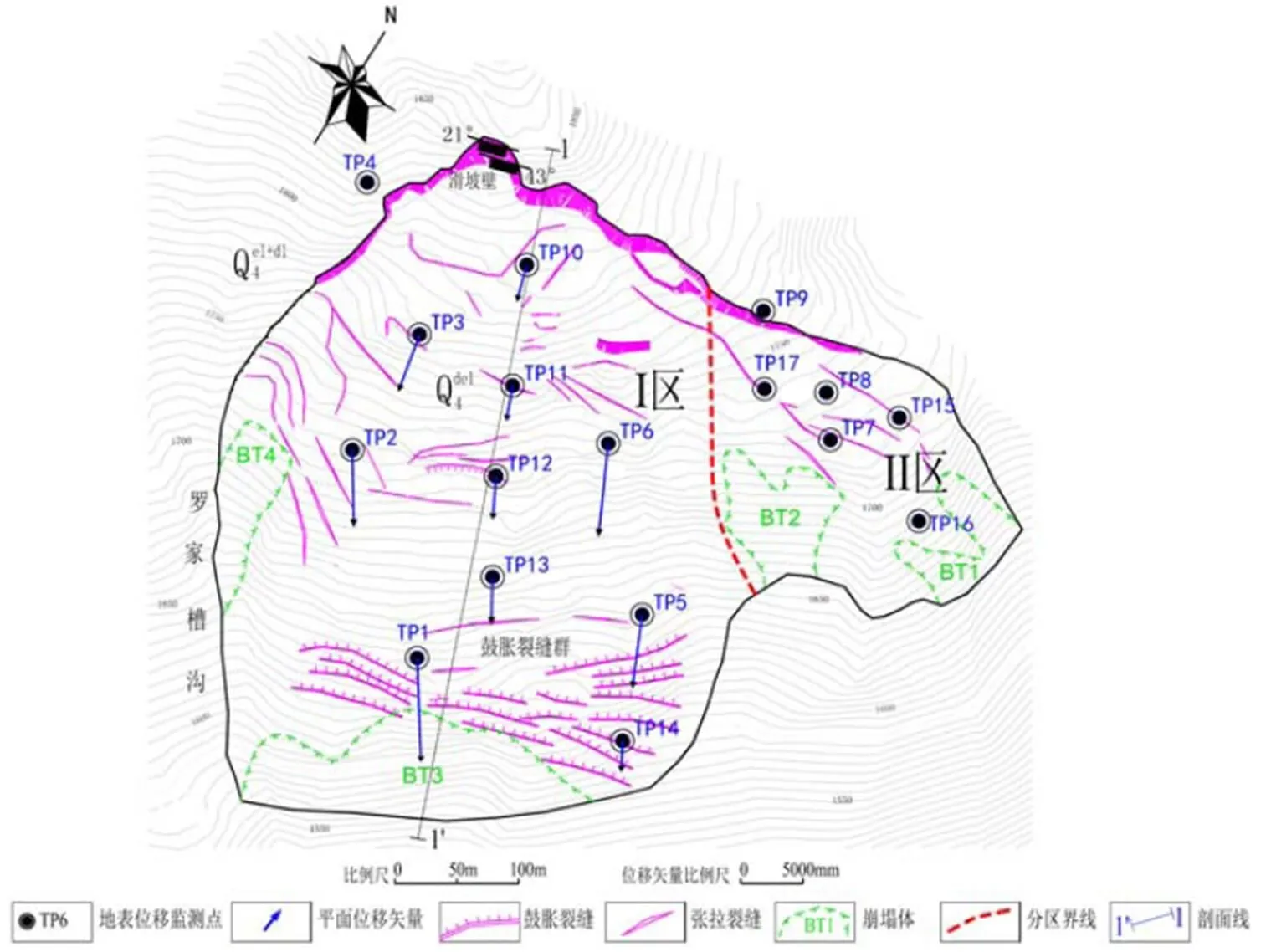
图2 白什乡滑坡监测平面图

2）回归模型只能描述随机变量与其他变量间的相关关系,而时序模型却能描述时序数据内部的一些相关关系。很明显,不是所有的随机过程都能找到特定的数学模型去表征的,而时序分析模型就能将随机过程中的规律用本身数据之间的相关关系来揭示。

3）进行时序分析应以输出等价为前提,即将所观测的时序数据应作为一个系统的一维或多维输出,而将模型描述的等价系统视为与输出同维的白噪声作用下产生的输出,这是对变形分析极为有利的。

4）从统计学角度来分析,时间序列分析也是为了揭示各时序数据内部以及时间数据之间的统计关系,所以时序分析也需要大量数据。

2 滑坡实例应用

2.1 工程概况

白什乡滑坡在平面上呈“圈椅状”，两侧边界明显，错开裂缝宽度不等。前缘为高差达500m，平均坡度大于45°的陡坡临空面，后缘出露滑坡壁，下错高度大于10m。滑坡体纵长为300m，平均宽度为260m，平均厚度为25m，总方量约200万m3。滑坡体前缘高程约1 530m，后缘高程约1800m。

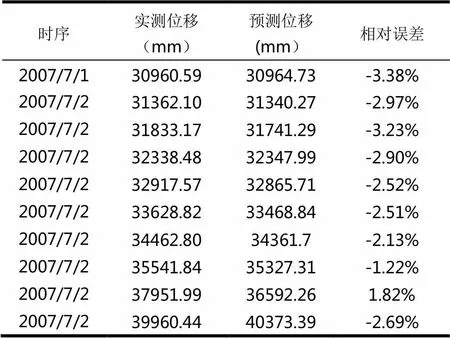
表1 实测数据与AMIRA(2,2,1)模型预测值对比表

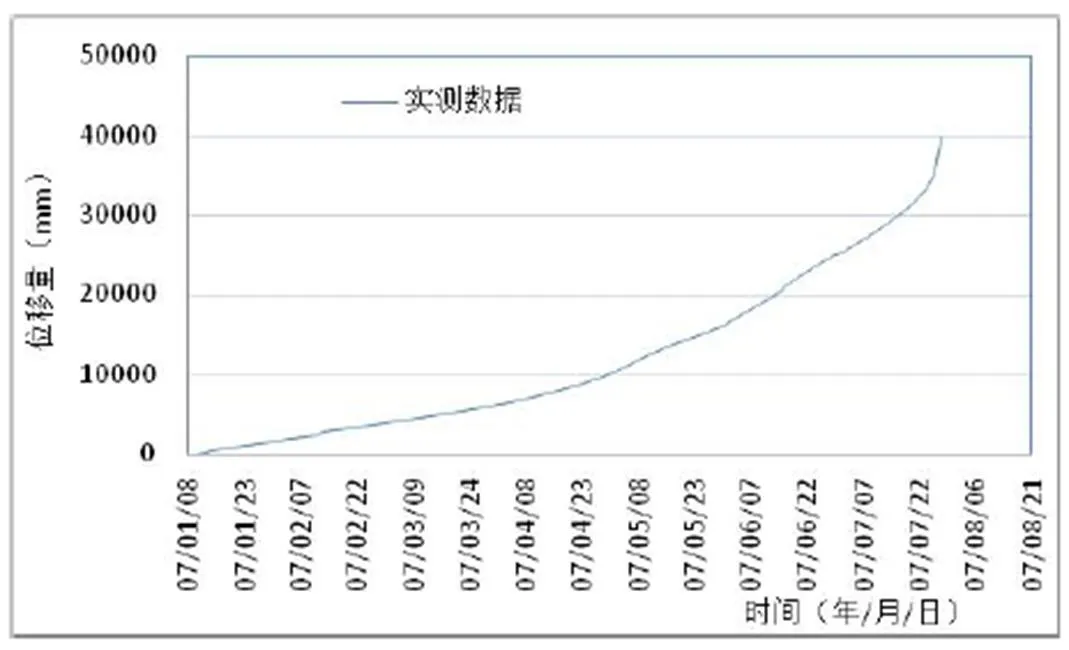
图3 监测点TP1累计位移-时间关系曲线图

通过现场调查，结合地形地貌及滑坡宏观变形特征，布设了9个地表位移监测点，编号TP1～TP17，监测点布置详见图2。选择具有滑坡前缘的变形敏感监测点TP1（2007年1月10月～2007年7月28日，监测次数为N=200）的位移时序资料。选取了前面190次观测数据进行时间序列建模，后10次观测数据用于时间序列模型预测对比。

2.2 数据平稳化预处理

首先对该数据进行平稳性检验，该数据具有明显的趋势性（图3），前期变形趋势较小，后期变形趋势较大，通过自相关性偏相关性以及存在着单位根，说明该监测点为非平稳数据。本文采用差分法对非平稳数据提取确定性信息，根据差分检验，本文采用了2阶差分，确定2阶差分序列均值方差稳定，详见图4。

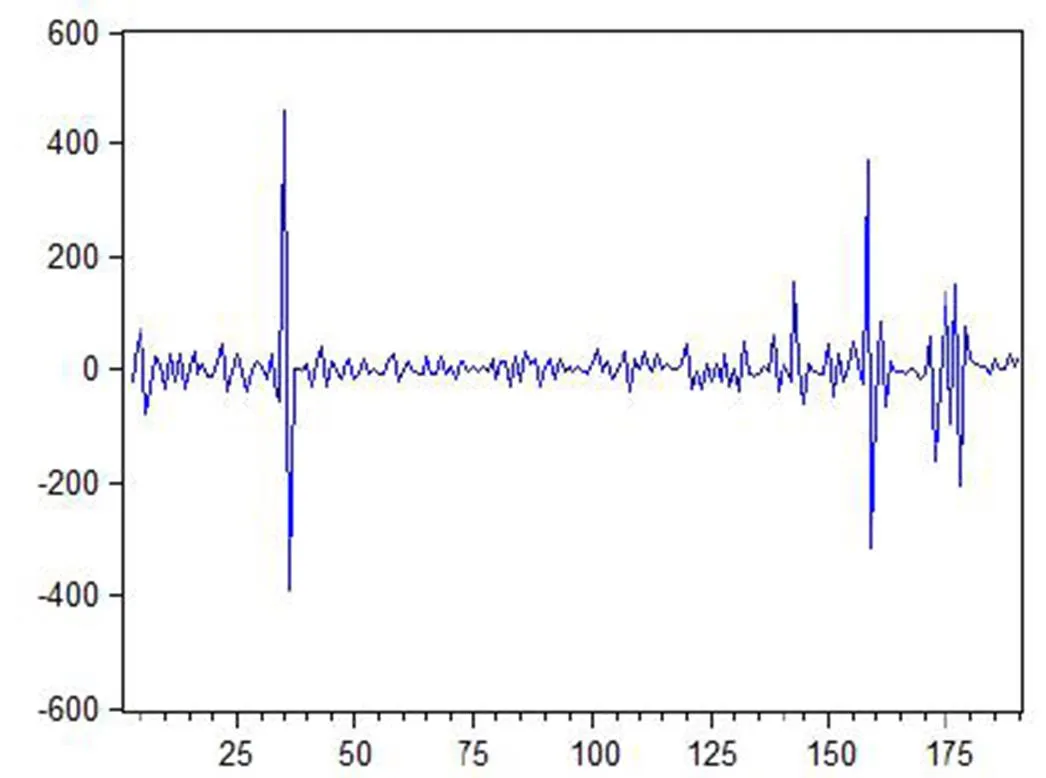
图4 2阶差分曲线图

图5可见经过差分处理后，各时滞的自相关系数已显著为0，且右侧一列的概率值都比0.05小，表明所有Q值都小于置信水平为0.05对应的χ2分布临界值,处理后的序列变为纯随机序列；且由图看出自相关系数在时滞为 1 后就开始迅速衰减为0，表明序列也已经平稳。观察2阶差分后序列d ( Dt) 的单位根ADF检验结果如图6，得到ADF统计量均小于临界值的结果，也表明2阶差分后的序列已经随机平稳。

2.3 模型的识别判断

对于ARIMA(p,a,q)模型，其中a为差分的阶数，可以利用其样本的自相关函数和偏相关函数的截尾性质来判定模型的阶数。若平稳时间序列的偏相关函数是截尾的，而自相关函数是拖尾的，则可判定此序列适合自回归（AR）模型；若平稳时间序列的偏相关函数是拖尾的，而自相关函数是截尾的，则可判定此序列适合移动平均（MA）模型；若平稳时间序列的偏相关函数和自相关函数是拖尾的，则此序列适合 ARMA 模型。

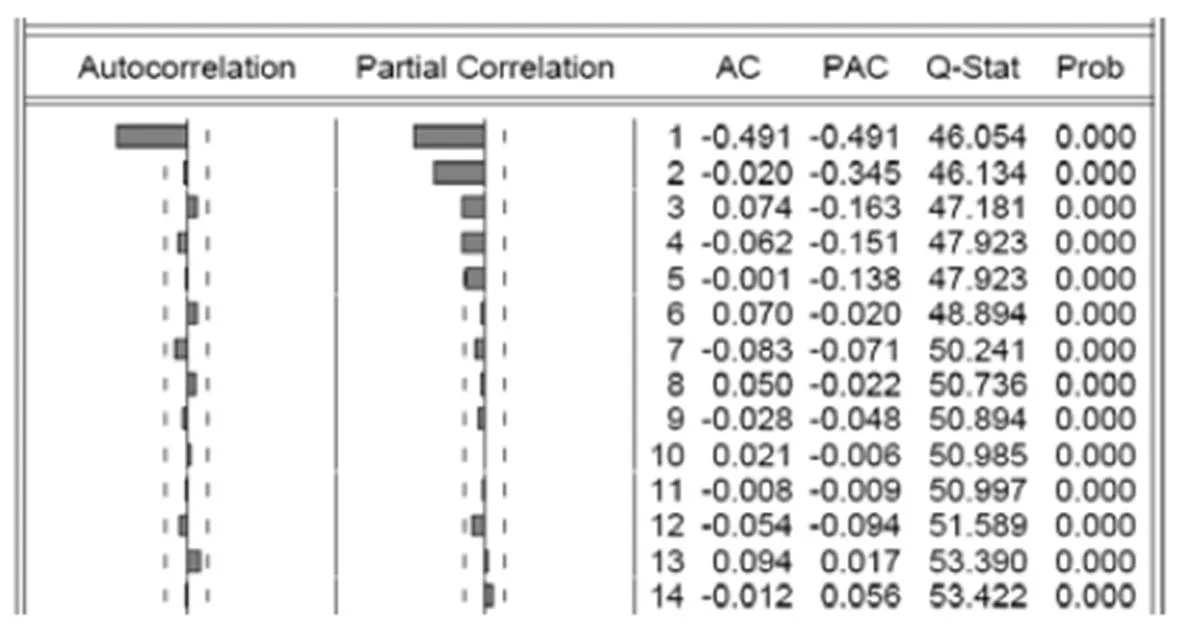
图5 数据的自相关和偏相关图

图6 ADF单位根检验图

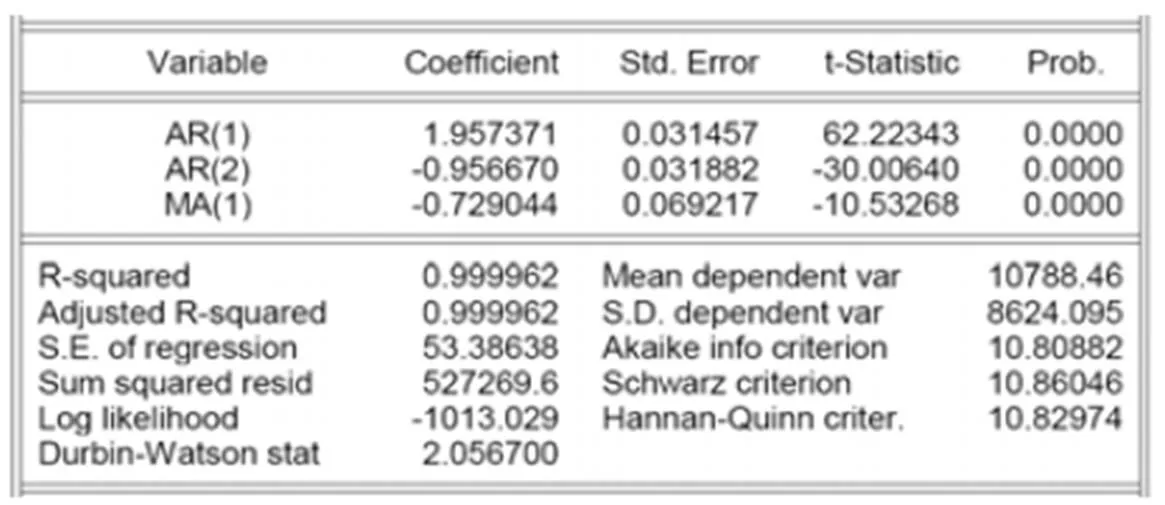
图 7 ARMA(2,1)模型参数估计结果

图 8 ARMA(2,1)模型残差 LM 检验结果

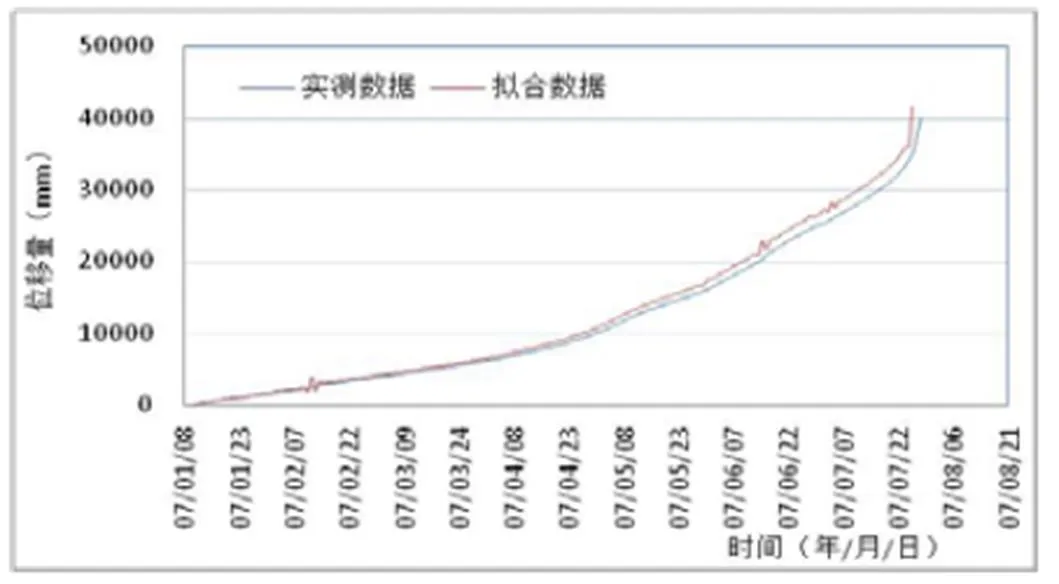
图9 实测数据与ARIMA(2,2,1)数据对比图

由图6可初步判定序列为 ARIMA(2,2,1)模型。同时应考虑临近的几个模型：AR(1)、AR(2)、MA(1)、ARIMA(1,2,1)和ARIMA(1,2,2)等。

选择模型参数的几个准则:

1) 信息量最小准则，即 AIC、SC 值越小越好，因为信息量越少模型越简洁。

2) DW 统计量范围准则，即 DW 值一般应介于 1.8~2.1 之间，说明模型残差为正态分布且不相关。

3) 模型精确准则，即在考虑以上准则时，需要兼顾模型残差的大小，应考虑残差平方和 RSS 和平均绝对百分误差 MAPE 等统计量的取值。

经过计算和检验，发现模型ARIMA（2,2,1）符合选择模型参数的准则，更加显著有效，对序列适应性更强。

2.4 模型的检验

对模型 ARIMA(2,2,1)的评价与检验一般指对模型残差的白噪声检验。若残差是非白噪声，说明残差中还存在可以提取的有用信息，还需要对模型进一步改进或重新建模。针对残差的检验一般采用有正态性检验、白噪声检验。正态性检验可通过LM检验法，结果如图8，其LM值0.0000对应概率为 0.3122，大于0.05，故残差服从正态分布。

2.5 滑坡位移预测

根据时间序列模型定阶结果，得到白川县白什乡滑坡地表位移位移监测点TP1累计位移量序列的模型ARIMA（2,2,1）表达式为：

高校所处外部政治经济环境不断变化，自身在不断发展中面临的风险和问题也在不断变化。而部分高校内控仅仅是流于形式的“一次性建设“，并没有根据高校内外部环境的变化进行改进和调整，内部控制措施和框架存在滞后性和不适应性。同时，高校内控缺乏长期规划性，缺乏相应的内控固化措施。

(1-B)2(1-φ1B-φ2B)Dt=(1-θ1B) ξt （4）

其中B为滞后算子，φ1、φ2为平稳序列的自回归阶数；θ1为平稳序列移动平均阶数。根据3.2~3.4计算结果，带入公式（4）中，可到到公式（5）：

(1-B)2*(1-1.96B-0.96B2)Dt=(1-0.73B)ξt （5）

通过最后10次实测数据与ARIMA(2,2,1)模型预测位移进行了对比，相对误差都在5%之内，说明了该模型是合理且适用的。但是模型仍然具有一定的局限性，适用于临滑预报，不宜作中长期预测。

3 结论

1）该研究考虑到传统滑坡位移变形预测方法的局限性，提出了滑坡坡位移的时间序列分析方法, 对建模具体过程及详细步骤进行了研究。

2）运用时间序列模型来揭示北川县白什乡滑坡位移变形规律拟合度高,预报效果好,误差也较小。

[1] 张闻胜，王银堂. 时间序列分解模型在水文要素中长期预报中的应用[J]. 水文，2001，21(1)：21-24.

[2] 张树京，齐立心. 时间序列分析简明教程[M]. 北京：北京交通大学出版社，2003：29–42.

[3] 卢 理. 时间序列加法模型的分解预测研究[硕士学位论文][D]. 成都：西南交通大学，2007.

[4] 郑璐石. 时间序列分析及其在岩土工程中的应用[J]. 宁夏大学学报（自然科学版），1995，16（4）：18-22.

[5] 徐峰，汪洋，杜娟，等. 基于时间序列分析的滑坡位移预测模型研究[J]. 岩石力学与工程学报，2011,30（4）:746-751.

[6] 李庆雷，马楠，付遵涛. 时间序列非平稳检测方法的对比分析[J]. 北京大学学报（自然科学版），2013,49（2）：252-260.

[7] 余宏明，胡艳欣，腾伟福.滑坡位移动态实时跟踪预测[J]. 地质科技情报,2001,20(2): 84-86.

[8] 王建锋. 滑坡发生时间预报分析[J]. 中国地质灾害与防治学报,2003,14(2):1-8.

[9] 缪海波, 殷坤龙，柴波, 等. 基于非平稳时间序列分析的滑坡变形预测[J]. 地质科技情报.2009,28(4):107-111.

[10] Robert C J，Martin K，Roman L．Time series of count data：Modeling，estimation and diagnostics[J]．Computational Statistics & Data Analysis，2006，51:2350-2364．

Study of Landslide Deformation Characteristics Based on Time Series Analysis

LIU Ya1CAI Jian-hua2DONG Jian-hui3

(1-China Southwest Geotechnical Investigation & Design Institute Co., Ltd., Chengdu, 610052; 2-China Railway Southwest Research Institute Co., LTD., Chengdu 611731; 3-School of Architecture and Civil Engineering, Chengdu University, Chengdu 610106)

An ARIMA prediction model of landslide displacement based on the landslide displacement monitoring data in Baishi landslide, Beichuan County, is established by using time series analysis method. Based on the self regression AR model and moving average MA model of landslide displacement prediction, the difference stationary process is used for calculating the partial displacement which, in combination with the forecasting values, obtains the total displacement prediction value and forecast model ARIMA (2,2,1) of the landslide monitoring point TP1. A displacement - time curve is obtained from measured and predicted values. The calculation results can well reflect the trend of the development and change of landslide displacement under the action of external factors which indicates that this model is effective and feasible in the prediction of landslide displacement.

landslide; displacement prediction; time series; AR; MA; ARIMA

P642.22

A

1006-0995（2017）02-0300-04

10.3969/j.issn.1006-0995.2017.02.030

2017-03-30

刘亚（1983-），男，四川安县人，工程师，主要从事岩土工程勘察、设计及地质灾害评价工作