基于单自由度的桨-轴回转振动特性分析

2017-07-05蒋炎坤

船电技术 2017年6期

田军，蒋炎坤

基于单自由度的桨-轴回转振动特性分析

田军，蒋炎坤

（华中科技大学能源与动力工程学院，武汉 430074）

基于受简谐激励的单自由度系统产生振动的机理,从理论上分析了偏心质量所引起的桨-轴系统回转振动特性，利用幅频特性曲线和相频特性曲线分析该系统稳态响应的动力学特征,探讨系统转速和偏心质量对桨-轴系统回转振动的影响。同时基于Ansys/workbench平台建立了桨-轴系统回转振动模型并进行仿真计算，对理论分析结果进行验证。结果表明，利用单自由度受简谐激励振动模型来分析转子系统回转特性是可靠的、准确的。

偏心质量受迫振动稳态响应仿真：

0 引言

船舶轴系的各种振动中，轴的回转振动[1,2]主要是由于轴系转子质量不平衡状况恶化造成的，如产品材质及加工精度不达标，螺旋桨由于受损导致质量不平衡，轴系安装对中精度不达标产生的动不平衡等等会使轴系回转振动加剧。在船舶的日常航行中由于偏心质量产生的振动从轴系开始运转就存在，严重的偏心质量振动会对轴系的正常旋转产生严重危害甚至会破坏机组，影响船舶航行[3]。

螺旋桨-轴-轴承组成的系统这里简称为桨-轴系统，轴承的安装位置、几何尺寸和轴承本身的固有特性，同轴本身的结构尺寸和材质一样，对轴系的动力特性和运转的稳定性有很大影响。因此，对船舶桨-轴系统回转振动特性和不平衡响应进行研究，对轴系的设计和改进轴系动平衡、降低机组回转振动等方面有重要的工程应用价值[4]。

这里从单自由度系统受简谐激励产生振动的机理[5]出发，建立振动模型，分析回转机械因偏心质量而引起的强迫振动，计算系统的稳态响应，利用幅频特性和相频特性分析系统稳态响应特征，探讨轴系各种特性参数对系统偏心质量机械振动的影响。同时在Ansys/workbench环境中，建立轴、轴承以及螺旋桨的几何模型，将材料选为45#钢。将螺旋桨简化为一个等效均质圆盘，转轴添加带支撑刚度和旋转阻尼的轴承及其支撑底座，并对转轴向添加轴向位移约束，进行仿真计算，然后验证理论分析结果。

2 单自由度有阻尼受迫振动系统力学模型

设质量为的质量块承受弹性恢复力、阻尼力c以及简谐激振力(t)=0sin等作用力，如图1所示。

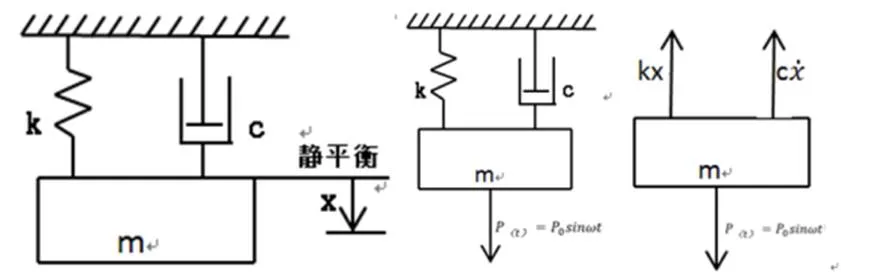
（a）（b）（c）

若以静平衡位置为坐标原点，取质量块的振动位移为广义坐标，且向下为正，则可按牛顿运动定律直接写出该系统的运动微分方程[6]：

+ c+kx=sin（1）

3 偏心质量引起的桨-轴回转振动

3.1 力学模型

在桨-轴系统中，回转振动激励的主要来源是偏心质量产生的离心力。假设系统质量均匀、形状规则，总质量为，本身不存在偏心质量，在螺旋桨边缘外加一个质量为的偏心质量块，偏心距为，轴的转动角速度是；两端轴承视为刚度为k/2的两个并联的弹簧，振动过程所受的阻力简化阻尼系数为c的阻尼器对轴的作用，从而偏心质量桨-轴系统的力学模型如图2所示。

3.2 振动分析

3.2.1 系统振动微分方程

设坐标为轴心离开平衡位置的垂直位移，根据达朗贝尔原理[6]可知，该回转系统在垂直方向的运动微分方程为：

（）+（+）+c+k=0 （2）

化简后得：

=sin（3）

该系统的运动微分方程与单自由度有阻尼受迫振动系统运动微分方程具有相同的形式，其中=为系统激励力的幅值。

因而，可以定义桨-轴偏心质量回转机械的运动可以等效于弹簧质量系统受到简谐激励力(t)=0sin=sin作用下的运动情况，为该桨-轴系统偏心质量产生的激励力的幅值。

图2 偏心质量回转机械模型图

3.2.2 系统振动的稳态响应

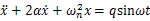
该非齐次二阶常系数线性微分方程的解为：

=Asin（）+B（5）

式中右边第一项表示有阻尼的自由振动（衰减振动），后一项表示有阻尼的受迫振动，由于自由振动会随着振动的进行而衰减，因而，在系统达到稳态的时候只存在第二项的受迫振动即：

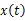
相应的，桨-轴系统在偏心质量产生的激励力(t)的作用下的振幅为：

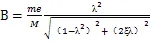
相位差为：

（9）

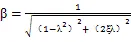
3.2.3 幅频响应曲线和相频响应曲线

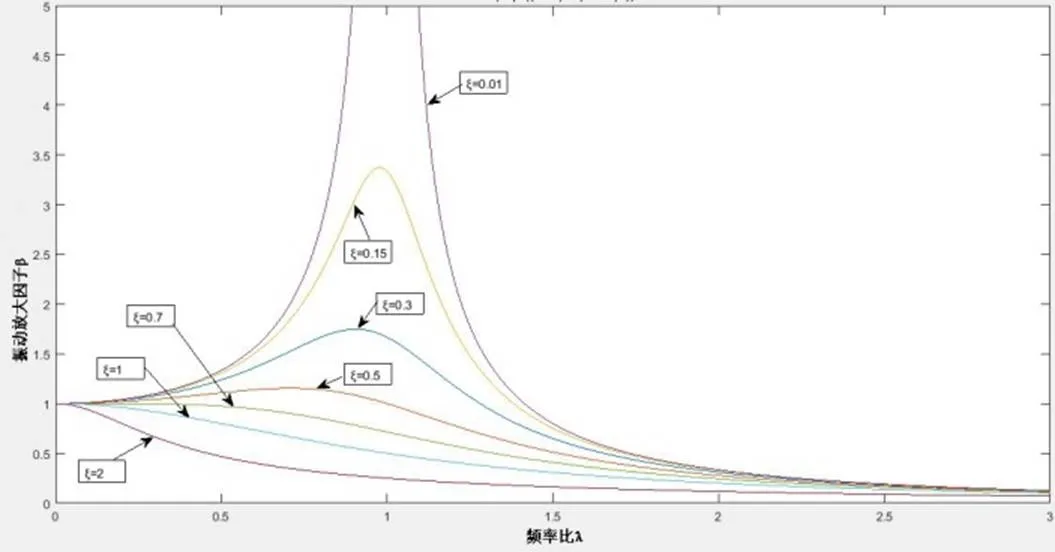
图 3 幅频响应曲线

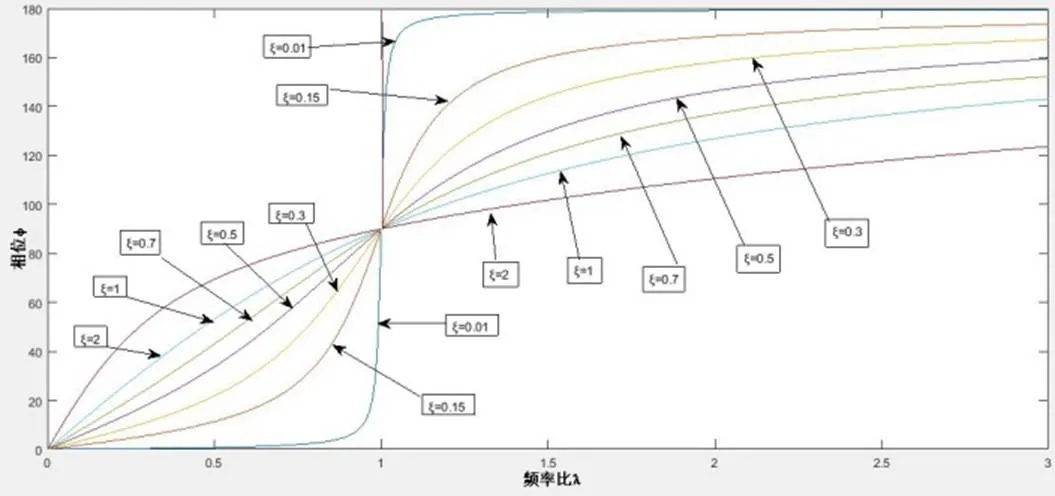
图 4 相频响应曲线

由式（8）、（9）和图3、图4可知：

1）转子系统偏心质量振动的响应幅值与偏心矩me成正比，振动相位与偏心量m无关；

2）在偏心矩、阻尼比等参数恒定时，振动响应的幅值和相位随旋转角速度的变化而变化。因此，在分析系统振动响应时必须结合转速进行。

3）当λ<1，即轴角频率低于固有频率时振幅B随角频率增大而逐渐增大；当λ>1时振幅B随角频率的增大而逐渐减小; 当λ=1时，振幅B达到最大，系统产生共振，此时系统振动频率与固有频率相同，对应的转速为临界转速。阻尼对振幅的影响表现为:在相同转速下，振幅随阻尼的增大而逐渐减小。

4）当轴角速度远小于固有频率时，相频响应接近为0，振幅接近于0.而当角速度远大于固有频率时，相频响应接近，振幅接近于常数，且与激振频率和系统阻尼无关。

4 偏心质量引起的桨-轴回转振动响应仿真计算

4.1 谐响应分析方法

谐响应分析是用于确定结构在承受按正弦（简谐）规律变化的载荷时的稳态响应分析方法[7,8]。分析目的是计算出结构在几种频率下的响应，并得到位移和相位随频率变化的特性曲线，从中找到“峰值”响应，并观察峰值频率处的位移。谐响应分析只计算结构的稳态受迫振动，不考虑在激励初期时的瞬态响应。

谐响应分析主要有完全法、缩减法和模态叠加法，下面针对所建模型采用完全法进行计算。

4.2 不平衡量的施加

模型中不平衡量主要是在需要添加不平衡量的位置施加集中力载荷，集中力量载荷是通过不平衡质量块对轴心产生的力矩来实现的。为不平衡力幅值，等于不平衡质量乘以偏心距。仿真中自动乘以角速度的平方得到不平衡量。

4.3 建立仿真模型

由于螺旋桨结构复杂，在结构参数缺乏的情况下难以建立精确的实体模型，故建立等效圆盘来简化模拟，并根据等效前后质量和转动惯量一致的原则，确定该圆盘的厚度和截面直径。这样 ,可以较精确地模拟实体螺旋桨的回转运动。有限元模型中圆盘作用点位置与实体螺旋桨作用点一致。桨-轴系统简化为带有3个刚性支撑的轴承—转子模型，其结构简图如图5所示。

图 5 桨-轴转子系统结构简图

轴系设备初始参数如表1所示。

通过在圆盘不同位置添加不同偏心质量块来获得不同的偏心距，计算并绘制轴系振幅响应图和相频响应图[9]。

桨-轴系统模态列如表2所示。

4.4 仿真结果分析

2）系统振幅随轴系角频率变化而变化，因而角频率是影响轴系振幅的重要因素；

3）在角频率在低于约9.2 Hz（即垂直一阶弯曲振动固有频率）之前，轴系响应振幅随角频率增大而增大；角频率在高于9.2 Hz之后，轴系响应振幅随角频率增大而减小；角频率等于9.2 Hz时，轴系响应振幅达到最大，约为26 mm。

表 1 轴系设备参数表

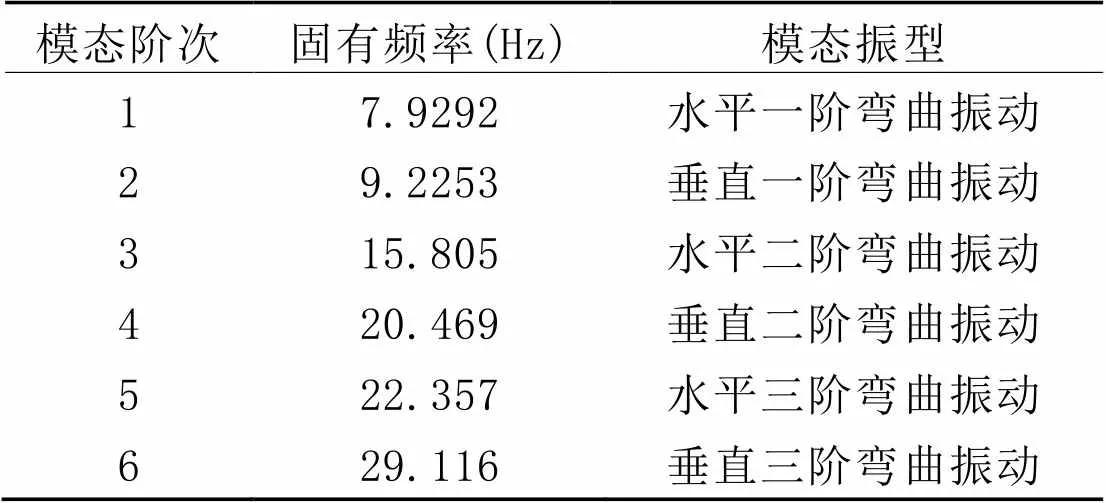
表 2 轴系固有特性表

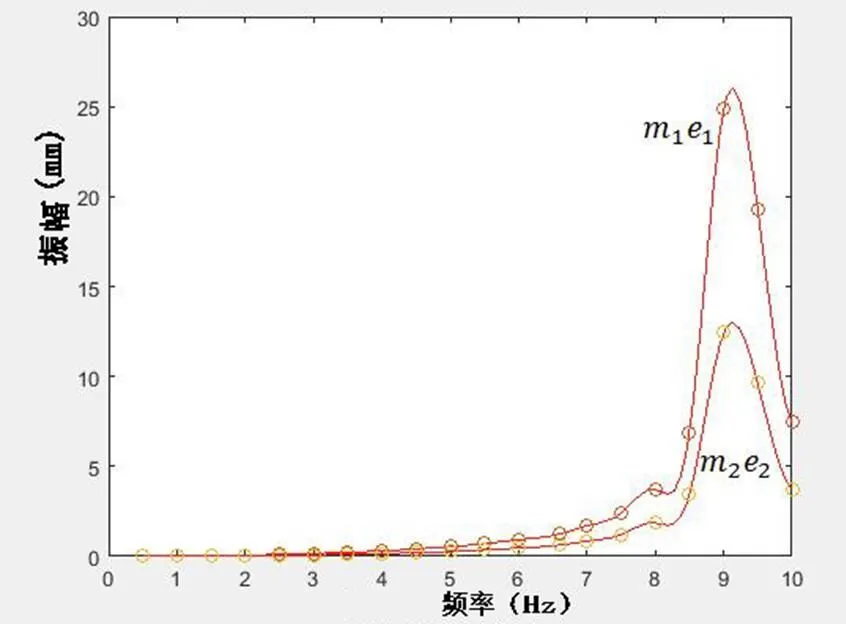
图 6 不同偏心距下轴的振幅响应

4）相频响应图如图7所示。

从图上可以看出在轴系角频率低于固有频率区间，轴系相频基本上接近于0；在角频率高于固有频率方向，相频突变为接近180°。

5 结论

上述结果表明: 振幅与系统不平衡量成正比。通过在Ansys/Workbench环境中建立模型，仿真结果与理论分析结论完全一致，证明了利用单自由度系统受简谐激励产生振动的机理，分析回转机械因偏心质量而引起的强迫振动的方法是可靠而准确的。这为我们分析偏心质量引起的振动提供了一个新的途径，而且分析过程简单易懂，有助于初学者对桨-轴系统偏心振动更深入的理解。建造桨-轴系统时必须确保加工精度，螺旋桨须做动平衡试验, 使质量尽可能均匀，当系统不平衡量得不到补偿时, 系统在即时将出现共振, 对整个桨-轴系统及其附属设备的性能和寿命产生很大影响, 甚至引起设备的损毁。共振时, 最大振幅为/2, 与阻尼成反比。这也为桨-轴系统提供了一条减振措施,即在不影响系统性能的前提下，提高系统阻尼来减小振幅。