Banach空间中Banach框架的扰动性

侯美琴, 姚喜妍

(1.山西师范大学 数学与计算机科学学院, 山西 临汾 041000; 2.运城学院 应用数学系, 山西 运城 044000)

Banach空间中Banach框架的扰动性

侯美琴1, 姚喜妍2

(1.山西师范大学 数学与计算机科学学院, 山西 临汾 041000; 2.运城学院 应用数学系, 山西 运城 044000)

运用算子论的方法,讨论了Banach空间中Banach框架的扰动性问题.给定X关于Xd的Banach框架({gi}i∈Ν,S)和有界算子T:Xd→X,探讨其在算子的作用下,得到新序列{φi}i∈Ν⊂X*使得({φi}i∈Ν,T)为X关于Xd的Banach框架;给定X关于Xd的Banach框架({gi}i∈Ν,S)和序列{φi}i∈Ν⊂X*,讨论其在序列的扰动下,存在有界算子U:Xd→X使得({φi}i∈Ν,U)为X关于Xd的Banach框架.同时表明已知结论是新结论的推广.

算子; Banach框架; 扰动性

0 引言

框架理论是研究小波分析的一个主要工具,它是由Duffin R.J.和Schaeffer A.C.在1952年研究非调和Fourier分析时提出的[1].近年来,许多算子理论与算子学者致力于小波与框架理论的研究,使得算子论方法成为框架理论研究中的一个充满活力的方法，尤其关于算子论与框架扰动性的结合更加活跃.但是,在Hilbert空间上研究框架的扰动性[2-9]，由于框架理论被广泛的应用于数学,信号处理等领域,从而将框架推广到Banach空间是非常有必要的.1991年,Groching[7]首次将框架的概念通过两种途径推广到Banach空间上,其为原子分解和Banach框架.随后出现了一系列关于这方面的结果,极大地丰富了框架理论.而框架扰动又是框架理论中活跃的研究方向,大量学者对Banach空间(Hilbert空间)上不同框架的扰动性进行了研究,得出一些有意义的结果[2-16].Casaza[5]在Banach空间上研究了有界线性算子扰动,李登峰、辛杰等人研究了Banach空间上原子分解和Banach框架的稳定性[14-15].

本文主要受文[14]的启发,运用算子论的方法,继续讨论Banach空间上Banach框架的扰动性,并对文[15]中的Banach框架的稳定性结果进行了推广.

引理1[5]设U:X→X是线性算子,若存在λ1,λ2∈[0,1)使得∀f∈X,‖Uf-f‖≤λ1‖f‖+λ2‖Uf‖则U:X→X是有界可逆算子,且

定理1[5]设U:X→Y是有界可逆算子,V:X→Y是线性算子,若存在λ1,λ2∈[0,1)使得∀f∈X,‖Uf-Vf‖≤λ1‖Uf‖+λ2‖Vf‖则V:X→Y是有界可逆算子,且

1){gi(f)}i∈Ν∈Xd;

2)∃A,B>0;A‖f‖≤‖{gi(f)}i∈Ν‖≤B‖f‖;

3)S({gi(f)}i∈Ν)=f，

则({gi}i∈Ν,S)为X关于Xd的Banach框架,S称为重构算子,A,B称为Banach框架界.

定义2[13]设X是Banach空间且Xd是以Ν为指标集的BK-空间,{gi}i∈Ν⊂X*,若对∀f∈X,

1){gi(f)}i∈Ν∈Xd;

2)∃A,B>0;A‖f‖≤‖{gi(f)}i∈Ν‖≤B‖f，

则{gi}i∈Ν是X的Xd-框架,框架界为A,B.

若满足定义2中的1)和2)中的右不等式,则{gi}i∈Ν是X的Xd-Bessel列.

1 主要结论

定理3 设({gi}i∈Ν,S)为X关于Xd的Banach框架,框架界为A,B,定义算子T:Xd→X是有界线性算子,U:X→X是有界可逆算子,若存在λ1,λ2>0,满足:

1)λ1,λ2∈[0,1)；

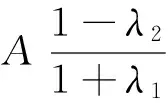
证明 令V:X→X,Vf=T({gi(f)}i∈N),则有‖Uf-Vf‖≤λ1‖Uf‖+λ2‖Vf‖,根据定理1知V:X→X是有界可逆算子,令φi=(V-1)*gi(∀i∈Ν),则对∀f∈X有

1){φi(f)}i∈Ν={(V-1)*gi(f)}i∈Ν={gi(V-1f)}i∈Ν∈Xd;

3)f=VV-1f=T({gi(V-1f)}i∈Ν)=T({φi(f)}i∈Ν)，

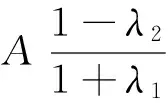
当U=I时,可得下面定理:

定理4 设({gi}i∈Ν,S)为X关于Xd的Banach框架,界为A,B,T:Xd→X有界线性算子,若存在λ1,λ2>0,满足:

1)λ1,λ2∈[0,1);

证明 令V:X→X,∀f∈X,Vf=T({gi(f)}),则有‖f-Vf‖≤λ1‖f‖+λ2‖Vf‖，根据引理1知:V:X→X有界可逆算子,令φi=(V-1)*gi(∀i∈Ν),则对∀f∈X,有

1) {φi(f)}i∈Ν={(V-1)*gi(f)}i∈Ν={gi(V-1f)}i∈Ν∈Xd;

3)f=VV-1f=T({gi(V-1f)}i∈Ν)=T({φi(f)}i∈Ν) ，

文[14]中的定理2.1是定理4的推论,即

推论1 设X是Banach空间,Xd是以Ν为指标集的BK-空间,设({gi}i∈Ν,S)为X关于Xd的Banach框架,界为A,B,T:Xd→X有界线性算子,若定义算子V:X→X,Vf=T({gi(f)})是可逆的,则存在则存在{φi}⊂X*使得({φi}i∈Ν,T)为X关于Xd的Banach框架,框架界为A‖V‖-1和B‖V-1‖.

文[2]中的定理4也是定理4的推论,即

推论2 设({gi}i∈Ν,S)为X关于Xd的Banach框架,框架界为A,B,定义算子T:Xd→X是有界线性算子,若存在λ1,λ2,μ≥0,满足下面条件:

1) max{λ2,λ1+μB}∈[0,1)；

推论3 设({gi}i∈Ν,S)为X关于Xd的Banach框架,框架界为A,B,定义T:Xd→X是有界线性算子,若存在λ1,λ2>0,满足下面条件:

1)λ1B,λ2∈[0,1),

证明 因为，对∀f∈X,

令V:X→X,∀f∈X,Vf=T({gi(f)}),则有‖f-Vf‖≤λ1B‖f‖+λ2‖Vf‖.根据定理1知V:X→X有界可逆算子,令φi=(V-1)*gi(∀i∈Ν),则对∀f∈X,有

1) {φi(f)}i∈Ν={(V-1)*gi(f)}={gi(V-1f)}i∈Ν∈Xd;

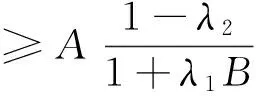
3)f=VV-1f=T({gi(V-1f)}i∈Ν)=T({φi(f)}i∈Ν)，

1)λ1,λ2∈[0,1);

2)‖g-TS*g‖≤λ1‖g‖+λ2‖TS*g‖，

则存在算子U:Xd→X使得({φi},U)为X关于Xd的Banach框架.

证明 设{ei}是Xd的基,令V=TS*:X*→X*,由题设知,对∀f∈X,有

‖g-Vg‖≤λ1‖g‖+λ2‖Vg‖,

即

则

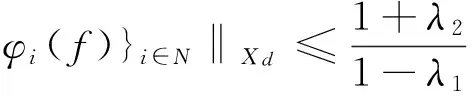
综上得

推论4 设Xd为自反且有基的Banach空间,({gi}i∈Ν,S)为X关于Xd的Banach框架,界为A,B,则存在序列{φi}⊂X*,λ1,λ2,μ>0若满足:

1) max{λ2,λ1+μ‖S‖}<1；

证明 对任意的∀n>m>0时,

‖g-TS*g‖≤λ1‖g‖+λ2‖T{di}‖+μ‖{di}‖,

即

c‖g-TS*g‖≤λ1‖g‖+λ2‖TS*g‖+μ‖S*g‖ ≤(λ1+μ‖S‖)‖g‖X*+λ2‖TS*g‖X*,

令V=TS*:X*→X*,则

‖g-Vg‖≤(λ1+μ‖S‖)‖g‖X*+λ2‖Vg‖X*,

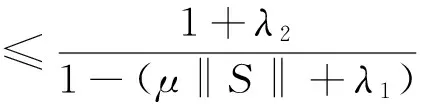
[1] Duffin R J,Schaeffer A C.A class of Nonharmonic Fourier Series[J].Trans Amer Math Soc,1952,72(3):341-366.

[2] Kato T.Perturbation Theory for Liner Operators[M].New York:Springer-Verlag Berlin Heidelberg,1984.

[3] Christensen O.Frame perturbations[J].Proc Amer Math Soc,1995,123(4):1217-1220.

[4] Christensen O.A paley-Wiener theorem for frames[J].Proc Amer Math Soc,1995,123(7):2199-2202.

[5] Casaza P G,Christensen O.Perturbation of operators and applications to frame theory[J].J Fourier Anal Appl,1997,3(5):543-557.

[6] Li D F,Yang L J.New perturbation results on frames in Hilbert spaces[J].Acta Mathematica Scientia,2008,28A(3):489-499.

[7] 周燕,曹月芬.K-g-框架扰动的稳定性[J].数学研究,2013,46(2):175-182.

[8] 李婵娟,朱玉灿.无冗K-框架的扰动性[J].福州大学学报(自然科学版),2014,42(6):807-811.

[9] 肖祥香,丁明玲.K-框架的冗余和扰动[J].福州大学学报(自然科学版),2013,41(2):143-147.

[10] 朱玉灿.Banach空间上的q-框架与p-Riesz基的稳定性[J].数学年刊,2001,22A(3):359-364.

[11] 李雪斌,朱玉灿.fusion-Riesz框架的算子扰动[J].福州大学学报(自然科学版),2014,42(2):173-182.

[12] Grochenig K.Describing functions:Atomic decomposition versus frames[J].Monatshefte fur Mathematik,1991,112(1):41-42.

[13] Casazza P,Christensen O,Stoeva D T.Frame expansions in separable Banach spaces[J].J Math Anal Appl,2005,307(2):710-723.

[14] 李登峰,杨利军.Banach空间上Banach框架和原子分解的扰动[J].数学物理学报,2009,29A(3):613-622.

[15] 辛杰,周家云.Banach空间的框架和原子分解的摄动及其稳定性[J].数学学报,2002,45(6):1165-1170.

[16] Stoeva D T.Perturbation of Frames in Banach Spaces[J].Asian-European Journal of Mathematics,2012,5(1):11-26.

[责任编辑：李春红]

Perturbation of Banach Frame in Banach Space

HOU Mei-qin1, YAO Xi-yan2

(1.School of Mathematics and Computer Science, Shanxi Normal University, Linfen Shanxi 041000, China) (2.Department of Applied Mathematics, Yuncheng University, Yuncheng Shanxi 044000, China)

The problem of perturbation of Banach frame in Banach space is discussed by using the operator theory. First, given the Banach frame ({gi}i∈Ν,S)forXwith respect toXdand the bounded operatorT:Xd→X, it is discussed under the action of the operator to obtain a new sequence {φi}i∈Ν⊂X*that makes({φi}i∈Ν,T) be a Banach frame forXwith respect toXd; secondly: Given the Banach frame ({gi}i∈Ν,S)for Xwith respect toXdand the sequence{φi}i∈Ν⊂X*, Under the perturbation of the sequence, there is a bounded operator making it for the Banach frame. At the same time, the article shows that the known conclusion is generalized by the new conclusion.

operator; Banach frame; perturbation

2017-01-04

山西省自然科学基金资助项目(20130111003-1); 山西省高校重点学科建设专项基金项目(20131010)

侯美琴 (1989-), 女, 山西朔州人，硕士研究生, 研究方向为算子理论与小波分析. E-mail: houmeiqin19@163.com

O177.1

A

1671-6876(2017)02-0095-05