电/磁特性参数对多铁性层合柱谐振断裂行为的影响
2017-07-05郭运坤张瑞芝李永东
郭运坤, 靳 莹, 张瑞芝, 张 俊, 李永东
(1. 装甲兵工程学院机械工程系, 北京 100072; 2. 中南大学数学统计学院, 湖南 长沙 410083)
电/磁特性参数对多铁性层合柱谐振断裂行为的影响
郭运坤1, 靳 莹1, 张瑞芝2, 张 俊1, 李永东1
(1. 装甲兵工程学院机械工程系, 北京 100072; 2. 中南大学数学统计学院, 湖南 长沙 410083)
针对多铁性复合材料谐振断裂力学问题,建立了谐振条件下多铁性层合柱动态断裂力学模型,然后应用分离变量法、无穷级数法、奇异积分方程和Lobatto-Chebyshev配点法研究了其谐振断裂行为,最后分析了压电系数、压磁系数、介电常数以及磁导率对应力强度因子(Stress Intensity Factor, SIF)一阶共振行为的影响。结果表明:在上述电/磁特性参数中,影响多铁性层合柱共振断裂行为的只有压电材料中的电特性参数和压磁材料中的磁特性参数。研究结果为多铁性智能器件的防断裂的优化设计提供了参考。
简谐振动; 动态断裂; 压电/压磁材料; 应力强度因子
多铁性智能器件(如传感器、浮能器和表声波器件等)大都在振动条件下工作,如:无损检测中的机电振动由机电换能器产生;频率超过200 kHz的超声检测通常使用压电换能器。与静态情况相比,振动条件下的多铁性复合材料更易于在界面或者内部产生损伤破坏,尤其当振动频率接近固有频率时。因此,研究振动条件下多铁性复合材料的断裂行为对智能器件的设计和应用是一项重要的基础理论工作,具有与静态断裂力学问题相区别的特殊工程意义。尽管由界面裂纹引起的静态断裂问题在近年得到了广泛研究[1-2],但关于界面裂纹引起的共振断裂问题鲜有报道。
基于此,笔者通过建立谐振条件下多铁性层合柱界面裂纹模型,应用分离变量法、无穷级数法、Lobatto-Chebyshev配点法和奇异积分方程对其谐振断裂问题进行研究,用应力强度因子(Stress Intensity Factor, SIF)作为评判断裂的参数,并利用 Mathematics软件进行编程和数值运算,主要分析了压电系数、压磁系数、介电常数以及磁导率对应力强度因子一阶共振行为的影响。
1 模型建立
图1为多铁性层合柱模型及笛卡尔直角坐标系。其中:内部为弹性层,中间为压磁层,外部为压电层,圆柱外表面半径由内向外分别为r1、r2和r3;坐标系的原点O与多铁性层合柱横截面的中心重合,x轴正方向通过裂纹中心,y轴垂直向上,z轴方向与x、y轴满足右手螺旋法则;压电层和压磁层之间的界面上存在一条中心角为2α的裂纹;假设压电层的外表面自由,压电层和压磁层均沿z轴极化,整个圆柱处于轴向的谐振之中,振动频率为ω。
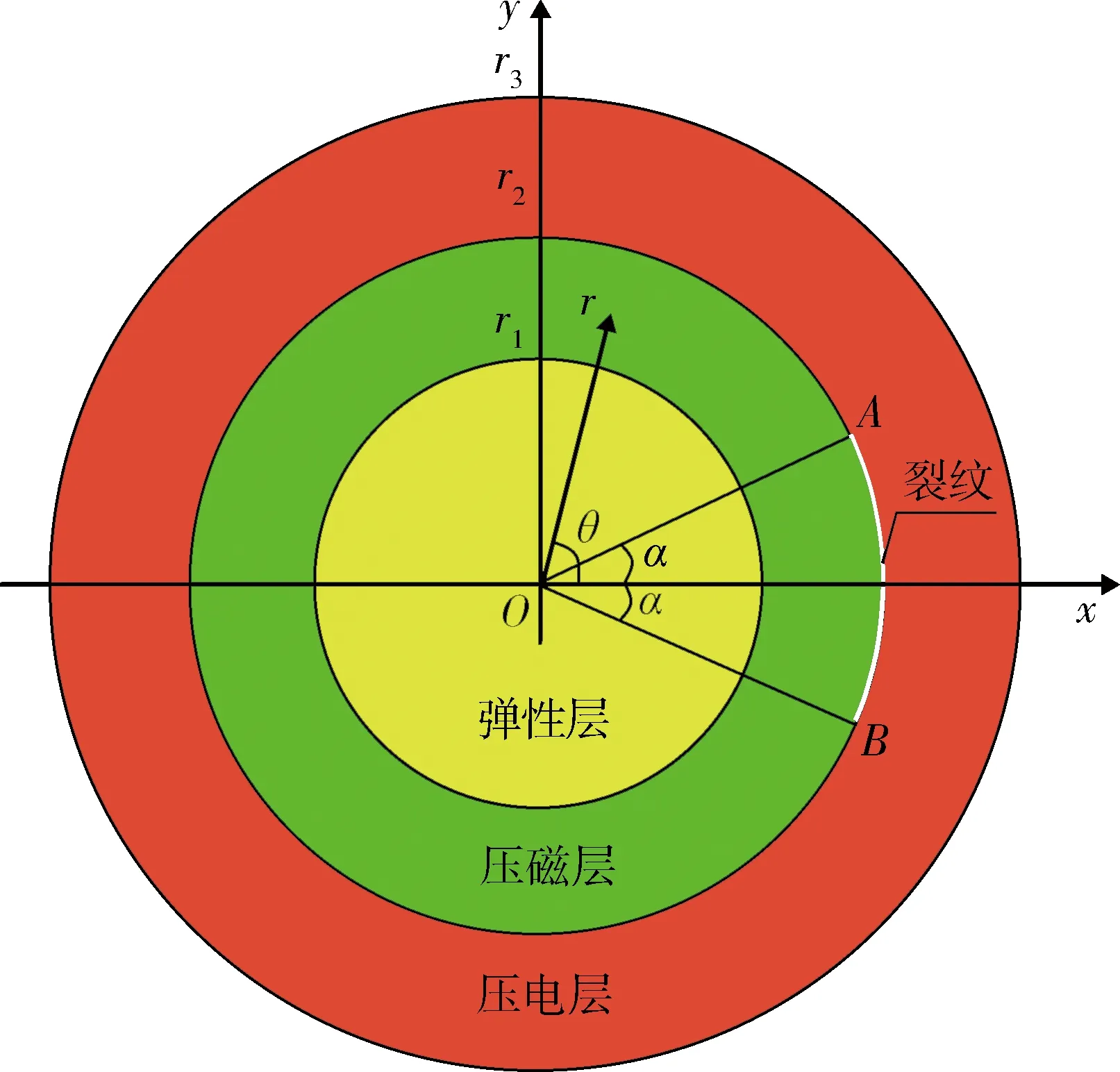
图1 多铁性层合柱模型及笛卡尔直角坐标系
忽略电磁感应的影响,则广义位移关系式可写成
w(r,θ,t)=w(r,θ)e-iωt,
φ(r,θ,t)=φ(r,θ)e-iωt,
φ(r,θ,t)=φ(r,θ)e-iωt。
(1)
式中:t为时间;e-iωt为时间因素(为简化公式推导与书写,下文将其省略)。
多铁性层合柱沿着z轴极化且具有横观各向同性。轴向剪切作用下3层材料的本构方程为
,
(2)
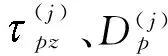
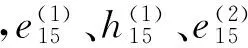
在谐振条件下,需要考虑多铁性复合材料的阻尼,一个比较科学且方便的方法是在剪切模量上乘以一个复数[3],即
(3)
式中:Gj为考虑阻尼的第j层剪切模量;ηj为第j层材料耗散系数。
当多铁性层合柱受到轴向稳定的简谐振动时,裂纹面保持闭合,可看作电磁可通。因此,内外表面及裂纹面的边界条件可表示为
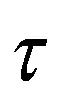
(4)
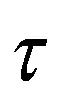
(5)
w1(r1,θ)=w2(r1,θ),
φ1(r1,θ)=φ2(r1,θ),
φ1(r1,θ)=φ2(r1,θ);
(6)
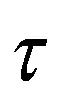
(7)
φ3(r2,θ)=φ2(r2,θ),
φ3(r2,θ)=φ2(r2,θ);
(8)
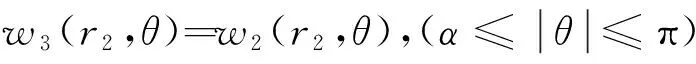
(9)
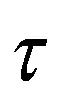
(10)
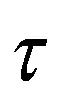
电位移散度方程、磁感应强度散度方程和运动方程分别为

(11)
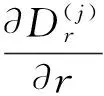
(12)
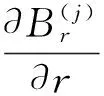
(13)
式中:ρj为第j层材料的密度。
2 断裂分析
2.1 广义位移与广义应力求解
把本构方程代入式(11)-(13)中,可得耦合偏微分方程为
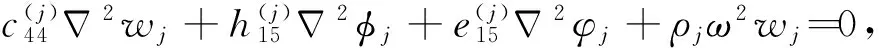
(14)
引入2个辅助函数[4]
(15)
对式(14)解耦,可得
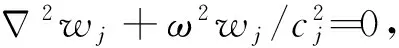
(16)

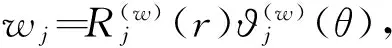
(17)
假设[5]
(18)
则式(16)可转化为
(19)
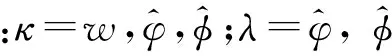
(20)

将式(20)代入式(1)中,得到广义应力表达式为
(21)
式中:

2.2 边界条件求解
边界条件(9)、(10)不能直接求解,为此引入位错密度函数
(22)
式(22)满足单值条件[6]
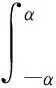
(23)
式中:g(s)为一个奇函数。
将式 (20)、(21)代入边界条件(4)-(8),并考虑式(22),可得一系列代数方程
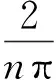
(24)
式中:Ω为边界条件代数方程系数矩阵;
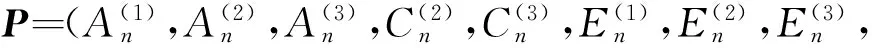
F=(1,0,0,0,0,0,0,0,0,
0,0,0,0,0,0)T。
求解式 (24),可得到系数表达式为
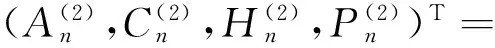
(25)
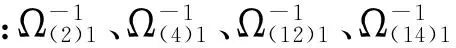
2.3 应力强度因子求解
将式(25) 代入式(21)中,得到裂纹面应力表达式为
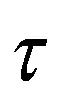
(26)
式中:
(27)
由式(27)可知:随着n的增大,Q(n)存在极限值
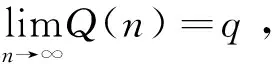
(28)
式中:q为与几何和物理常数有关的系数。在式(26)中的Q(n)上加减q,则裂纹面应力转化为
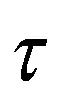
(29)
令ξ=cosθ,ζ=coss,则式(29)的标准形式为[5]
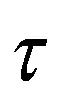
(30)
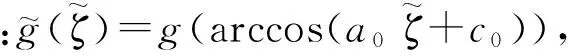
将式(30)代入式(10), 得到裂纹面等效载荷方程为
(31)
式(31)为标准柯西奇异积分方程。式中:
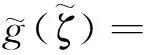
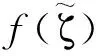
利用Lobatto-Chebyshev配点法[7]对式(31)进行离散求解,可得
(32)
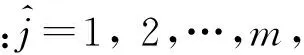


(33)
所研究多铁性层合柱裂纹模型属于Ⅲ裂纹,因此选应力强度因子SIF作为断裂参数[5]
(34)
由于剪切模量取成复数,因此Mathematics软件计算得到无量纲核函数与应力强度因子也为复数,下文对它们取模进行数据分析。
3 数值计算和参数分析
假设弹性层为聚乙烯,压磁层为CoFe2O4, 而压电层为BaTiO3。表 1 为具体材料系数取值。

表1 材料系数取值
3.1 核函数收敛性判别

图2 不同谐振频率下核函数收敛性曲线
3.2 参数分析
采用控制变量法研究了电/磁特性参数对多铁性层合柱谐振断裂行为的影响。其中:几何参数r3-r2=r2-r1=5 mm,r1=5 mm;阻尼系数η1=η2=η3=0.05;电/磁系数参数缩放倍数依次为0.7、0.8、1.0、1.2、1.3和0.7、1.0、1.3。
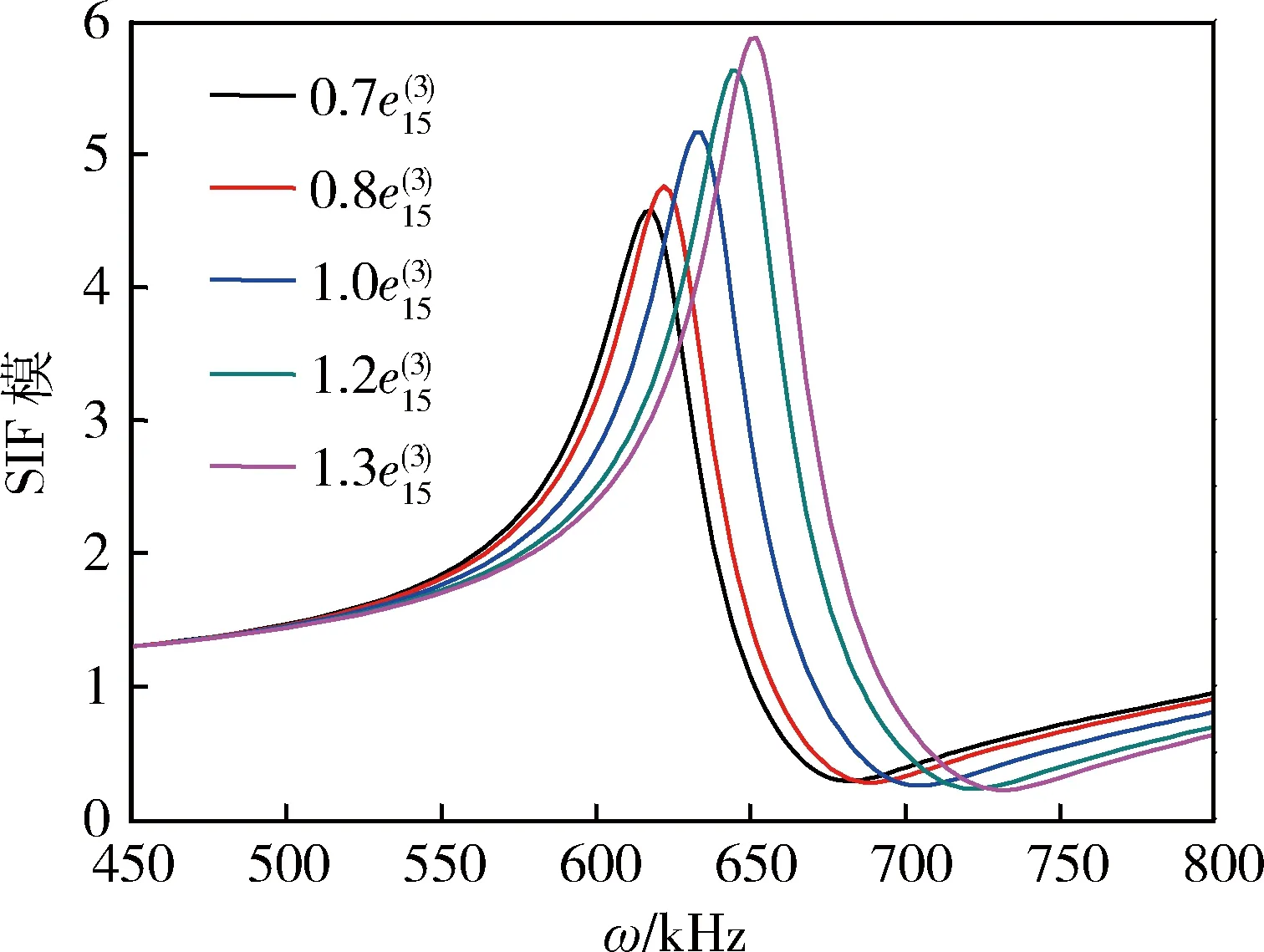
图3 压电系数对SIF一阶共振行为影响曲线

图4 压磁系数对SIF一阶共振行为影响曲线
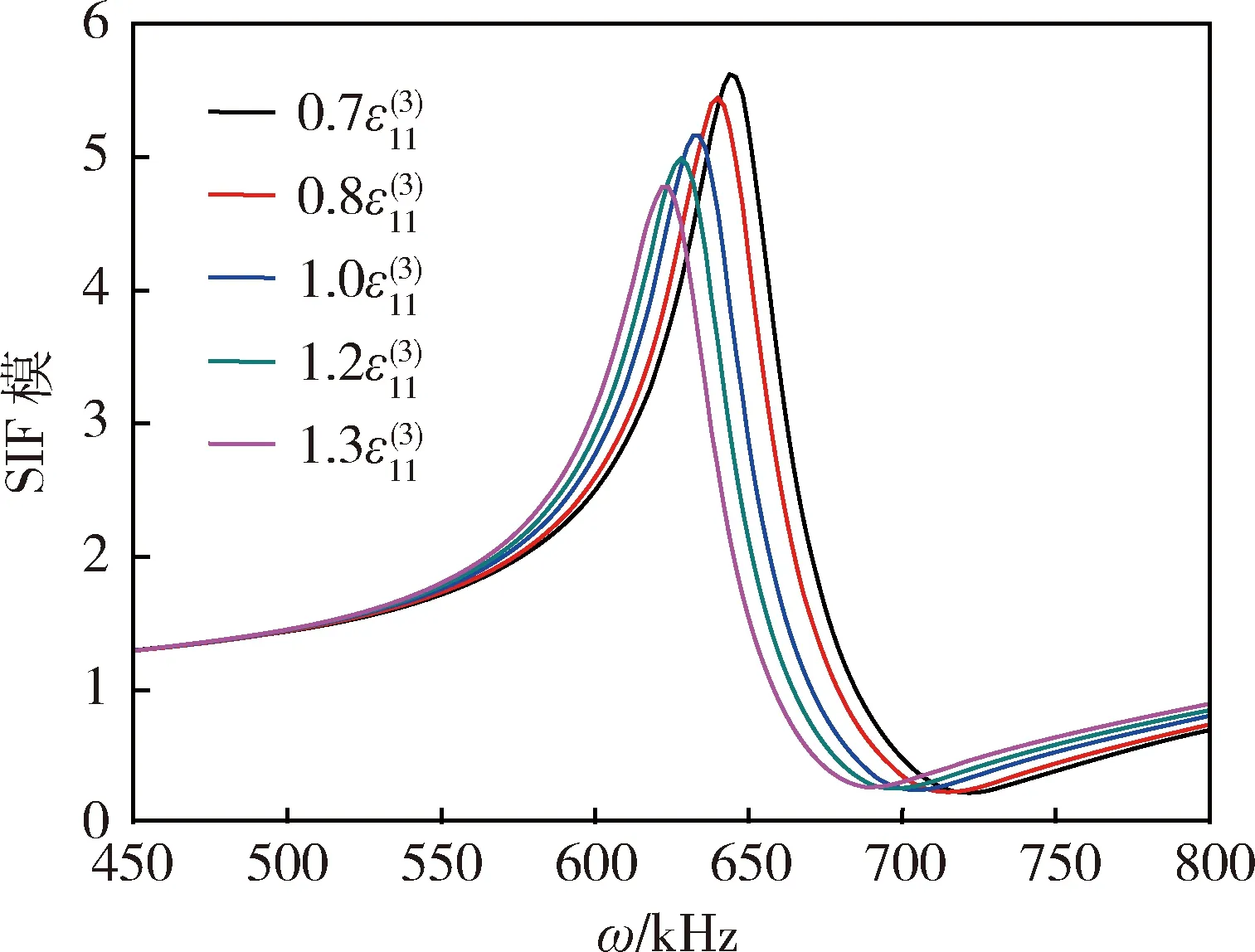
图5 介电常数对SIF一阶共振行为影响曲线

图6 磁导率对SIF一阶共振行为影响曲线
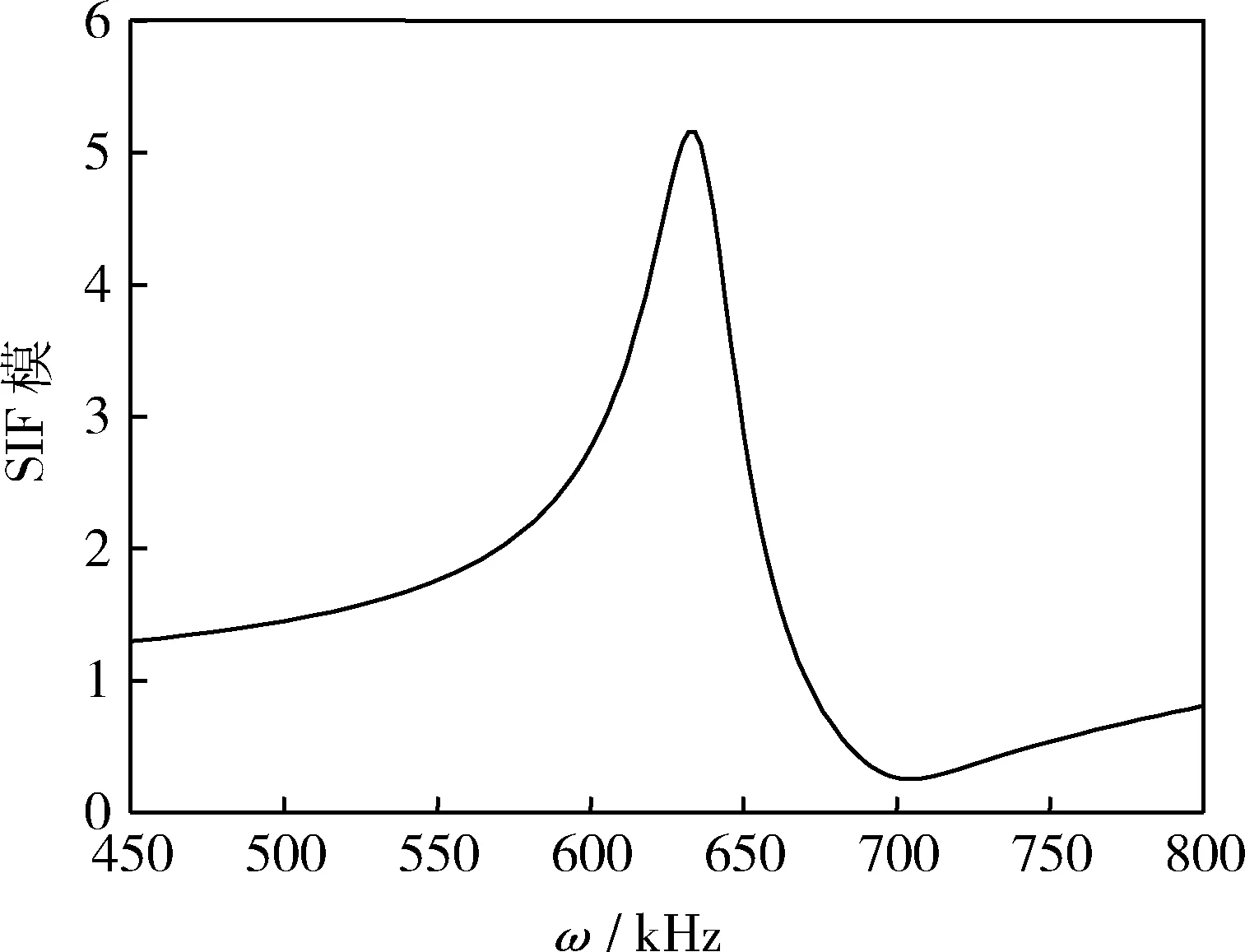
图7 磁导率与介电常数系数对SIF一阶共振行为影响曲线
4 结论
通过多铁性层合柱谐振断裂力学行为分析可知:影响其共振断裂行为的有压电材料的压电系数和介电常数以及压磁材料中的压磁系数和磁导率;而弹性材料的介电常数及磁导率、压电材料的磁导率和压磁材料的介电常数的改变不会对共振断裂行为产生影响。上述结论可为多铁性智能器件防断裂优化设计提供理论参考。
[1] LI X Y,ZHENG R F,KANG G Z,et al.Closed-form field in an infinite space of transversely isotropic multiferroic composite medium with an elliptical or penny-shaped crack: 3D exact analysis[J].International journal of solids and structures,2016,80:96-117.
[2] LI Y D,FENG F X,ZHAO H.Multiple interfacial cracks in a bi-layered multiferroic composite under magnetostriction or electrostriction[J].Engineering fracture mechanics,2012,90:65-75.
[3] GUO Y K,LI Y D,PAN J W.Effects of complex modulus and residual stress on the vibration induced resonant fracture behavior of a multiferroic cylindrical structure[J].Engineering fracture mechanics,2017,171(1):98-109.
[4] LI Y D,XIONG T,GUAN Y.Effects of coupled interfacial imperfections on SH wave propagation in a layered multiferroic cylinder[J].Ultrasonics,2016,66:11-17.
[5] LI Y D,LEE K Y.Fracture analysis on the arc-shaped interface in a layered cylindrical piezoelectric sensor polarized along its axis[J].Engineering fracture mechanics,2009,76(13):2065-2073.
[6] WEERTMAN J.Dislocation based fracture mechanics [M].Singapore:World Scientific Publishing Co Inc,1996.
[7] THEOCARIS P S,IOAKIMIDIS N I.Numerical integration me-thods for the solution of singular integral equations[J].Quarterly of applied mathematics,1977,35(1):173-183.
(责任编辑: 尚菲菲)
Effects of Electrical and Magnetic Characteristic Parameters on Resonant Fracture Behavior of a Multiferroic Cylindrical Structure
GUO Yun-kun1, JIN Ying1, ZHANG Rui-zhi2, ZHANG Jun1, LI Yong-dong1
(1. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China;2. Institute of Mathematics and Statistics, Central South University, Changsha 410083, China)
In order to study the resonant fracture mechanics behavior of multiferroic composite material, a mechanical model is established for the dynamic fracture problem of a multiferroic cylindrical structure subjected to simple harmonic vibration. The resonant fracture behavior is studied by the combined me-thods of variable separation, infinite series, singular integral equation and Lobatto-Chebyshev collocation, and the effects of piezoelectric, piezomagnetic, dielectric coefficients and magnetic conductivity on the first order resonance behavior of Stress Intensity Factor (SIF) mainly are analyzed. The results show that, among the above electrical and magnetic characteristic parameters, only can the electrical characteristic parameters of the piezoelectric ceramics and magnetic characteristic coefficients of the piezomagnetic material affect fracture resonance behavior in the multiferroic cylindrical structure. The obtained conclusion can provide guidelines for the anti-fracture optimal designs of multiferroic devices.
simple harmonic vibration; dynamic fracture; piezoelectric/piezomagnetic composites; Stress Intensity Factor (SIF)
1672-1497(2017)03-0100-06
2017-03-28
国家自然科学基金资助项目(11372358)
郭运坤(1993-),男,硕士研究生。
O346.1
A
10.3969/j.issn.1672-1497.2017.03.019
