涡流脉冲热像中金属疲劳裂纹检测条件优化方法

冯辅周， 徐 超， 闵庆旭， 孙吉伟， 朱俊臻

(装甲兵工程学院机械工程系, 北京 100072)



涡流脉冲热像中金属疲劳裂纹检测条件优化方法

冯辅周， 徐 超， 闵庆旭， 孙吉伟， 朱俊臻

(装甲兵工程学院机械工程系, 北京 100072)

为了探究不同检测条件对裂纹生热特性的影响及其最优化的选择，采用控制变量法探究了提离距离、激励强度和激励时间等检测条件对裂纹区域生热的影响规律。基于检测条件对裂纹生热的影响分析，采用多元非线性回归模型估算了特定检测条件下裂纹检出概率(Probability Of Detection, POD)，最终确定了检测条件的优化选择范围。上述检测条件的优化方法为涡流脉冲热像(Eddy Current Pulsed Thermography,ECPT)检测中检测方案的制定提供了理论指导。

涡流脉冲热像； 检出概率； 热响应； 疲劳裂纹

涡流脉冲热像(Eddy Current Pulsed Thermography，ECPT)无损检测,是近年来国际上迅速发展起来的一项检测结构件表面缺陷和亚表面缺陷的无损检测技术，它具有快速、准确、安全和检测效率高等特点[1-2]，能够很好地适应对复杂形貌的浅表裂纹和贯穿裂纹的检测需求。在检测特定对象之前，需要确定涡流脉冲热像的激励强度、激励时间和提离距离等检测条件，不同的检测条件组合对表面温度的分布影响不同[3]；而检测条件优化的关键在于建立检测条件与缺陷生热的对应关系[4]。然而，由于装置性能的变化、环境因素的干扰等必然会影响实际检测环节，对同一缺陷的重复测量或许会产生不同的检测结果。因此，实践过程中主要通过建立检测条件和缺陷检出概率(Probability Of Detection， POD)[5]之间的关系实现检测条件优化。HOLLAND等[6-8]在简单梁结构上施加共振激励，建立激励强度、裂纹尺寸和裂纹热信号之间的关系，并提出了一种评估超声振动热像检出概率的可行策略。GAO等[9]围绕航空发动机扇叶的裂纹检测问题，提出了一种基于线性混合效应模型的检测条件优化方法，给出了特定检测条件下检出概率随裂纹尺寸的变化曲线。

目前，国内检测条件优化研究大都采用超声激励，而对涡流脉冲激励的研究甚少。基于此，笔者以热响应信号与检测条件之间的对应关系为切入点，以单个含贯穿裂纹的金属平板为研究对象，揭示了检测条件对裂纹热响应的影响规律，在此基础上确定检测条件在多元非线性回归模型中变量的形式，最后结合检出概率给出了检测条件的优化选择范围。

1 实验装置及方案

1.1 实验装置

图1为涡流脉冲热像检测实验台，主要包括激励电源、电磁线圈、水冷装置和三维运动平台4部分。本实验台能够定量控制激励时间、激励强度和提离距离等检测条件，其主要技术参数为：额定功率为3 kW，工作频率为200600 kHz，定时范围为030 s，激励强度范围为1%100%(精度1%)，热像仪采集频率为30 Hz，温度分辨率为0.035 ℃。

图1 涡流脉冲热像检测实验台

实验中所用被测平板为240 mm×47.4 mm×5 mm的45钢，其长边一侧人工预制长度为9.301 mm的疲劳裂纹，如图2所示。测试前，在被测平板表面喷涂黑色哑光漆，以提高表面发射率。

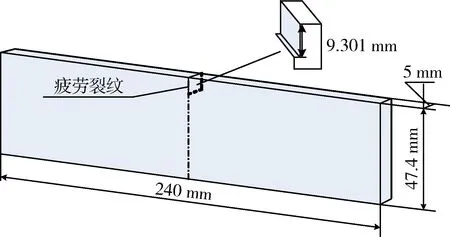
图2 被测平板示意图

1.2 实验方案

采用控制变量法探究提离距离、激励强度和激励时间等检测条件对裂纹区域生热的影响及特点，其取值范围及水平梯度如表1所示，其中：激励强度采用最大功率(3 kW)的百分比表示。

表1 各检测条件的取值范围及水平梯度

实验时，红外热像仪通过采用激励同侧安装的方式获得最大的裂纹热响应信号，取选定区域内部温升(减背景后)3次重复测量的平均值为热响应值。裂纹热响应的选定区域如图3所示。

图3 裂纹热响应的选定区域

2 检测条件影响分析

2.1 提离距离

保持激励强度(30%、60%、100%)和激励时间(200 ms)等检测条件不变，提取出不同提离距离下裂纹区域热响应。图4为热响应随提离距离变化的分布规律及拟合曲线。可以看出：当提离距离为015 mm时，裂纹热响应随提离距离的增大而增大；当提离距离为1550 mm时，裂纹热响应随提离距离的增大而衰减。这说明在一定的提离距离内，提离距离对裂纹区域生热存在显著影响。

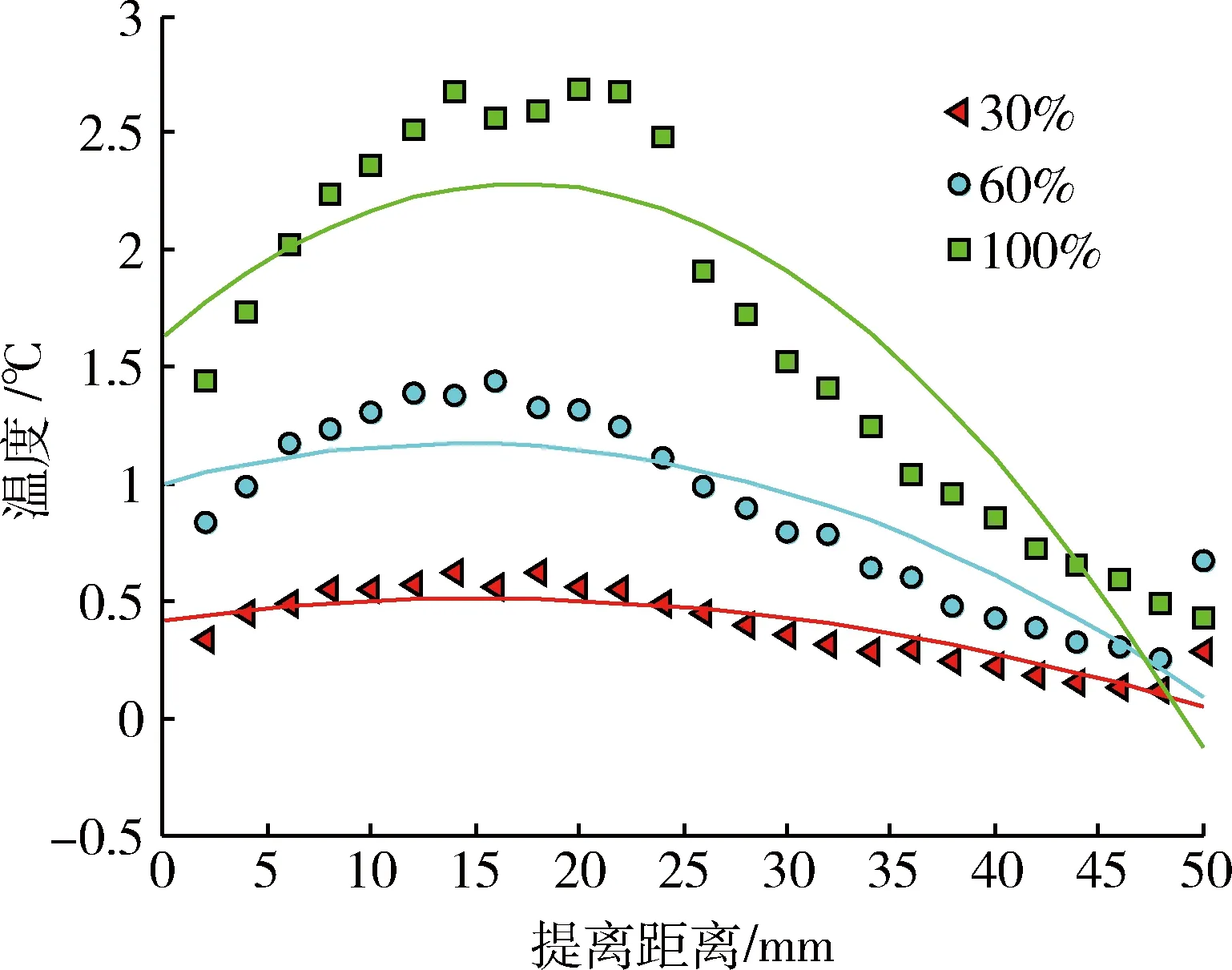
图4 热响应随提离距离变化分布规律及拟合曲线

2.2 激励强度

保持激励时间(50、100、200 ms)和提离距离(15 mm)等检测条件不变，提取不同激励强度下裂纹区域热响应。图5为热响应随激励强度变化的规律及拟合曲线。可以看出：拟合效果较好，且不同激励时间下裂纹热响应整体上随激励强度的增加而增大，这说明激励强度对裂纹区域生热满足正相关性。

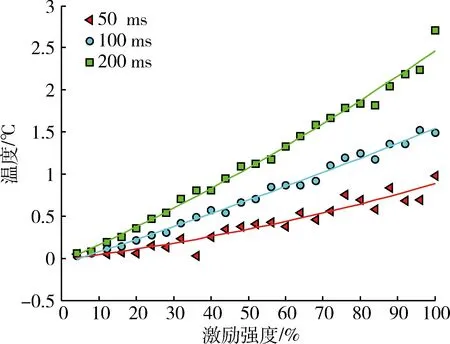
图5 热响应随激励强度变化规律及拟合曲线

2.3 激励时间

保持激励强度(30%、60%、100%)、提离距离(15 mm)等检测条件不变，提取出不同激励时间下裂纹区域热响应。图6为热响应随激励时间变化的分布规律及拟合曲线。可以看出：拟合效果较好，裂纹热响应随激励时间的延长而增大，且近似地呈线性关系变化，这说明涡流激励下裂纹的生热效率基本恒定。

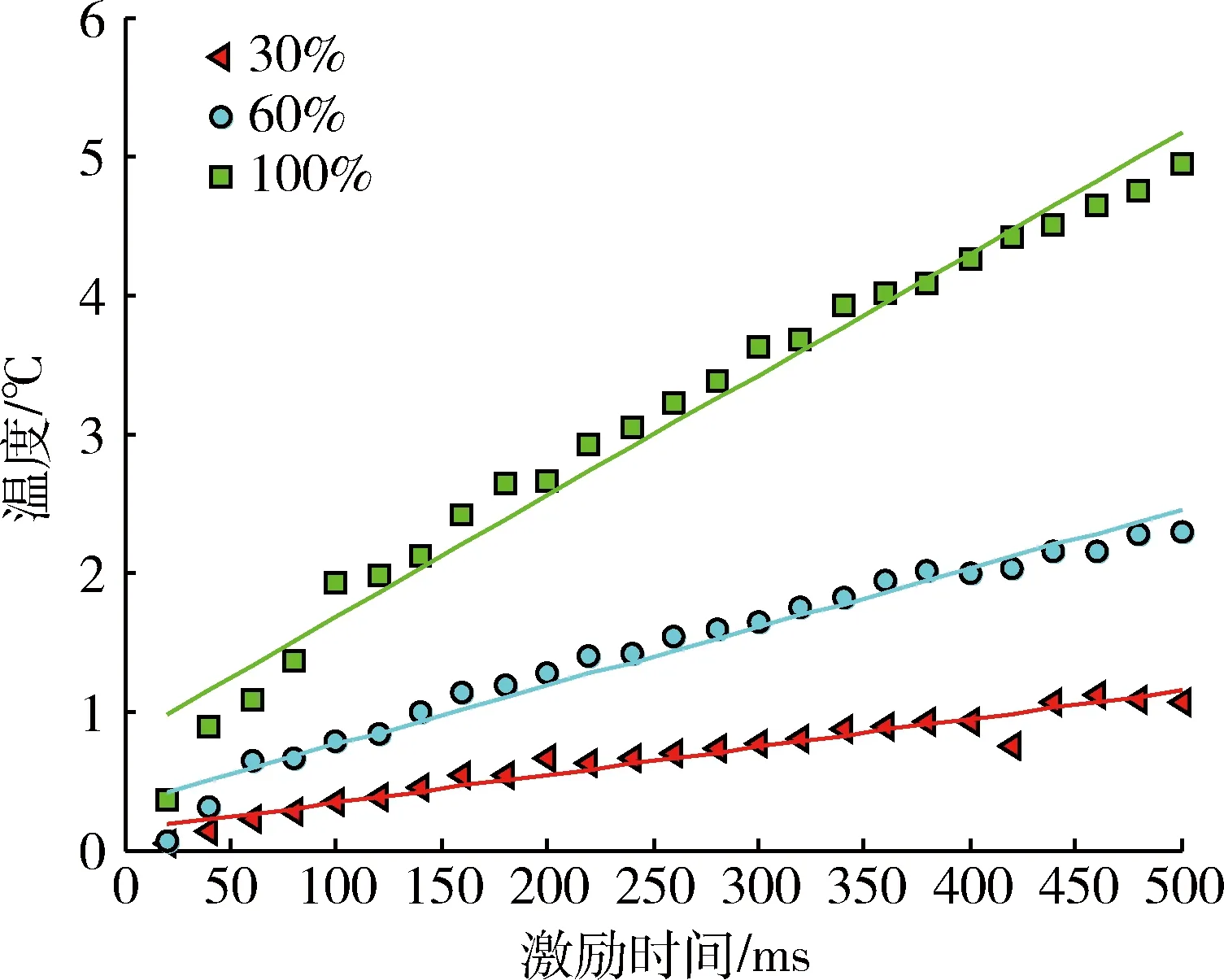
图6 热响应随激励时间变化规律及拟合曲线

3 检测条件优化

3.1 测试方案设计

对任何一种无损检测技术而言，多次检测可提高检出概率，而检测效率的提高与检出概率的提高是一个相互矛盾的问题，因此选择检测条件时必须综合考虑。综合考虑POD模型的要求和保证能够完整地描述裂纹热响应的变化规律，以3个检测条件为自变量，分别在各自的取值范围内选择5个水平。检测条件水平如表2所示。

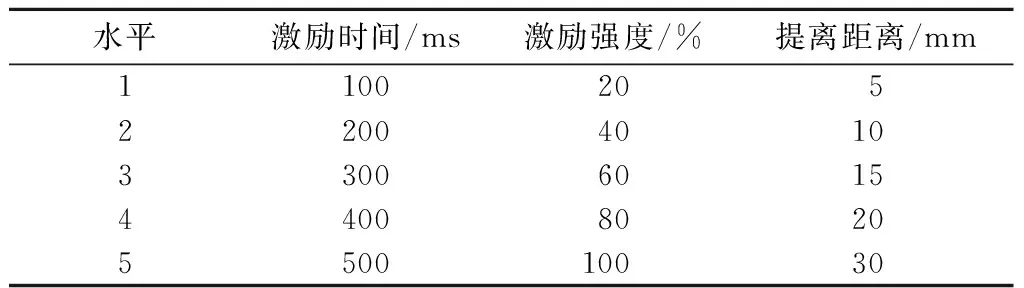
表2 检测条件水平

3.2 多元非线性回归模型

由第2节的结论易知：不论激励强度和提离距离如何组合，裂纹热响应必然与激励时间呈线性关系，则裂纹热响应与激励强度、提离距离的关系可采用二次多项式描述。同时，引入各检测条件之间的交叉项，得到裂纹热响应与检测条件的多元非线性回归模型为

β6Tl+β7Ti+ β8li+β9Tli+σ,

(1)

式中：T为激励时间；l为提离距离；i为激励强度；σ为误差项;β0，β1，…，β9为多元非线性回归模型中各项参数。

3.3 参数筛选

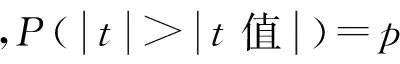
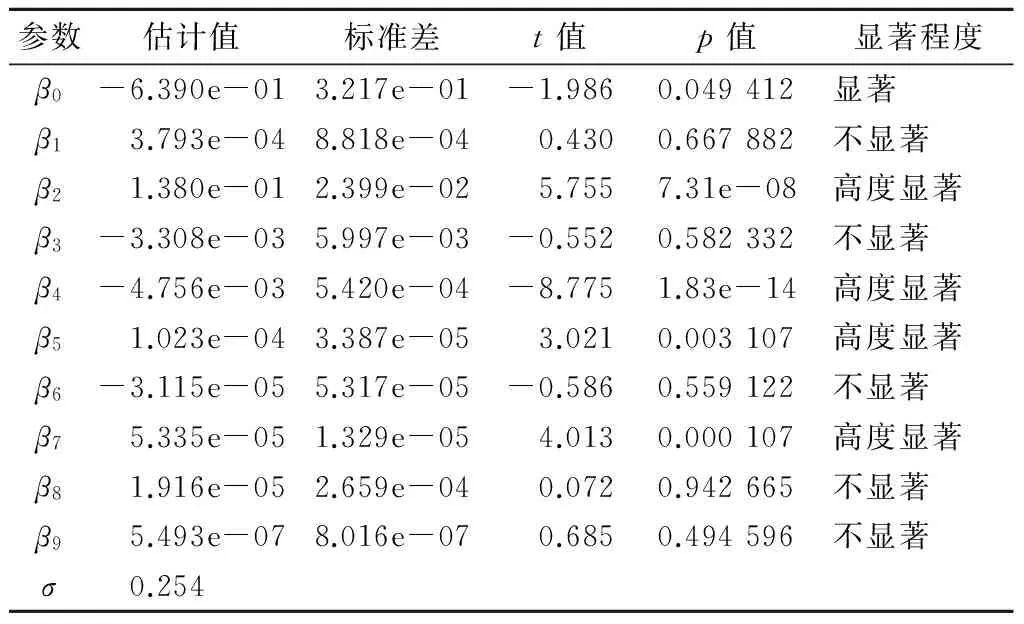
表3 多元非线性回归模型未知参数估计值

利用AIC值和R语言中的Step函数对上述回归模型中的不显著变量进行逐一筛选，结果如表4所示。AIC值最小时对应的回归模型即为优化模型。由表4可知：优化模型为

(2)

表5为优化模型未知参数估计值。

表4 筛选结果

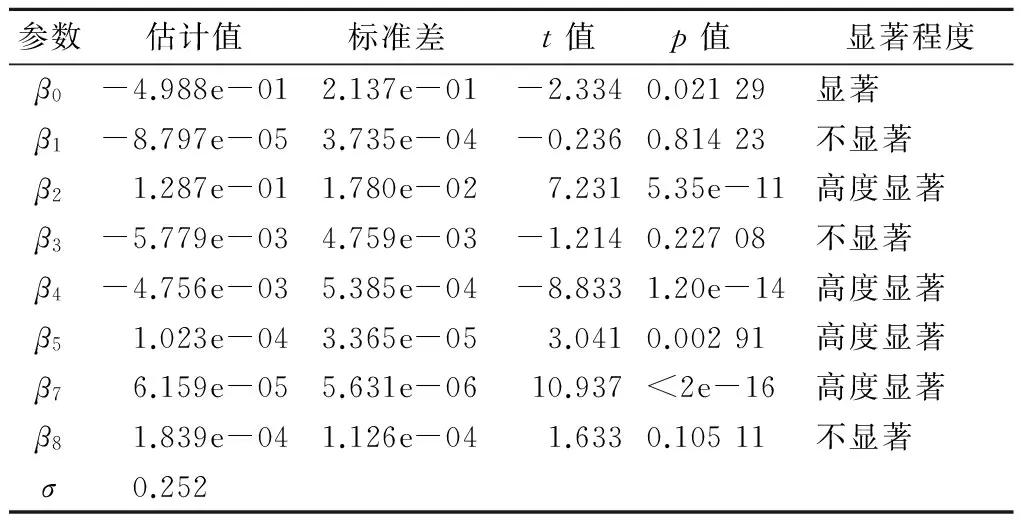
表5 优化模型未知参数估计值

进一步筛选掉表5中的不显著项(P>0.05)，最终得到的最优拟合模型为

(3)

表6为最优拟合模型的未知参数估计值，结合式(3)不难看出：裂纹热响应受3个检测条件共同影响，但由于β5和β7的值相对较小，则对应项中的激励强度i和激励时间T对模型的结果影响较小，因此裂纹热响应主要受提离距离l的影响；模型中出现了激励强度i的二次项，说明裂纹热响应与激励强度i之间并不满足简单的正相关性，与图5所得结论不符，这是因为图5中仅考虑了单一检测条件对裂纹热响应的影响。

表6 最优拟合模型未知参数估计值

图7为激励时间分别为100、200、500 ms时，提离距离和激励强度对裂纹热响应的影响规律。可以看出：裂纹热响应的等值线分布并不均匀，这是由于2个检测条件组合对热响应存在交互影响的缘故；激励时间为100、300、500 ms的裂纹热响应结果具有相似性，说明该结果具有普遍性。

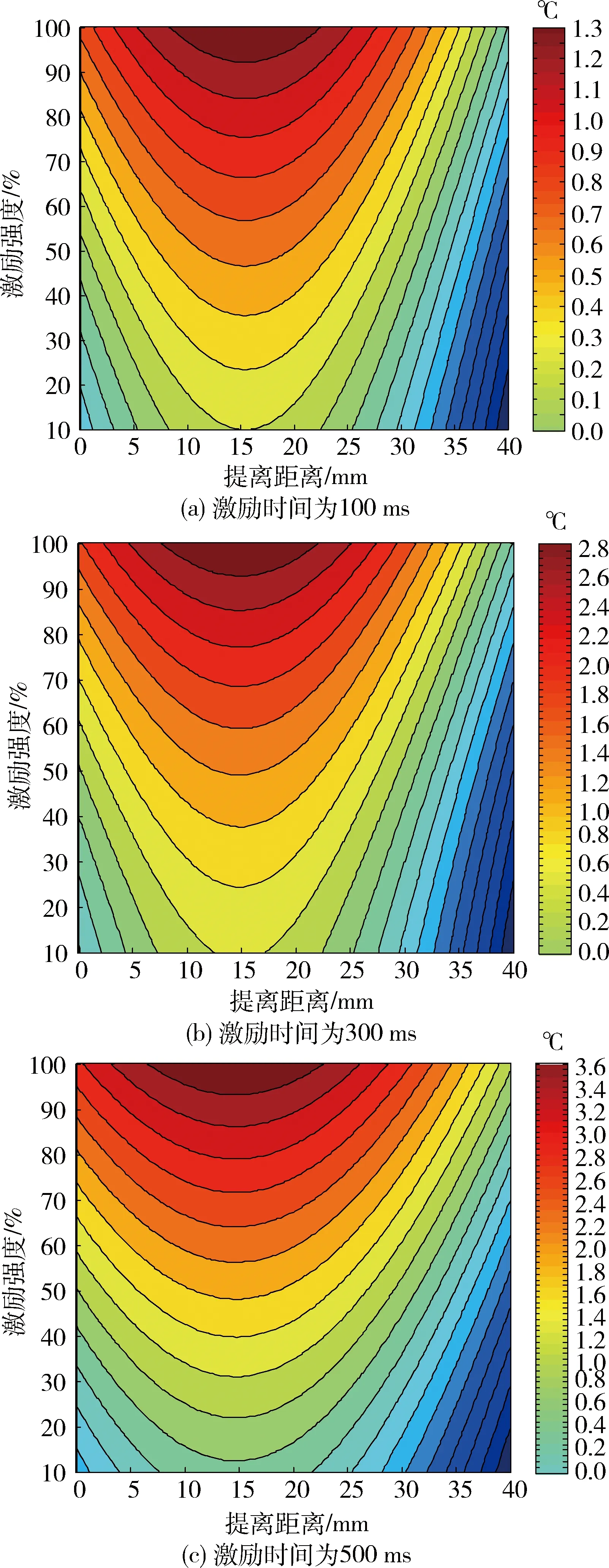
图7 不同激烈时间下提离距离和激励强度对裂纹热响应的影响规律

3.4 检测条件优化

利用表6中各参数估计值得到最优拟合模型结果，进一步根据文献[4]中的POD模型计算检出概率。由于最优拟合模型中激励时间T的参数β7较小，因此本文控制激励时间，只研究了激励强度和提离距离的优化组合。

图8为激励时间为200 ms、判定阈值为0.5 ℃(根据检测经验确定，一般为σ的23倍)时，检出概率随检测条件变化的分布云图，其颜色越亮表示检出概率越大。可以看出：较大的激励强度和适当的提离距离组合能够显著提高裂纹的检出概率。因此，在检测过程中，检测条件应尽量选取在白色区域范围(POD>95%)内，即检测条件优化选择区域。

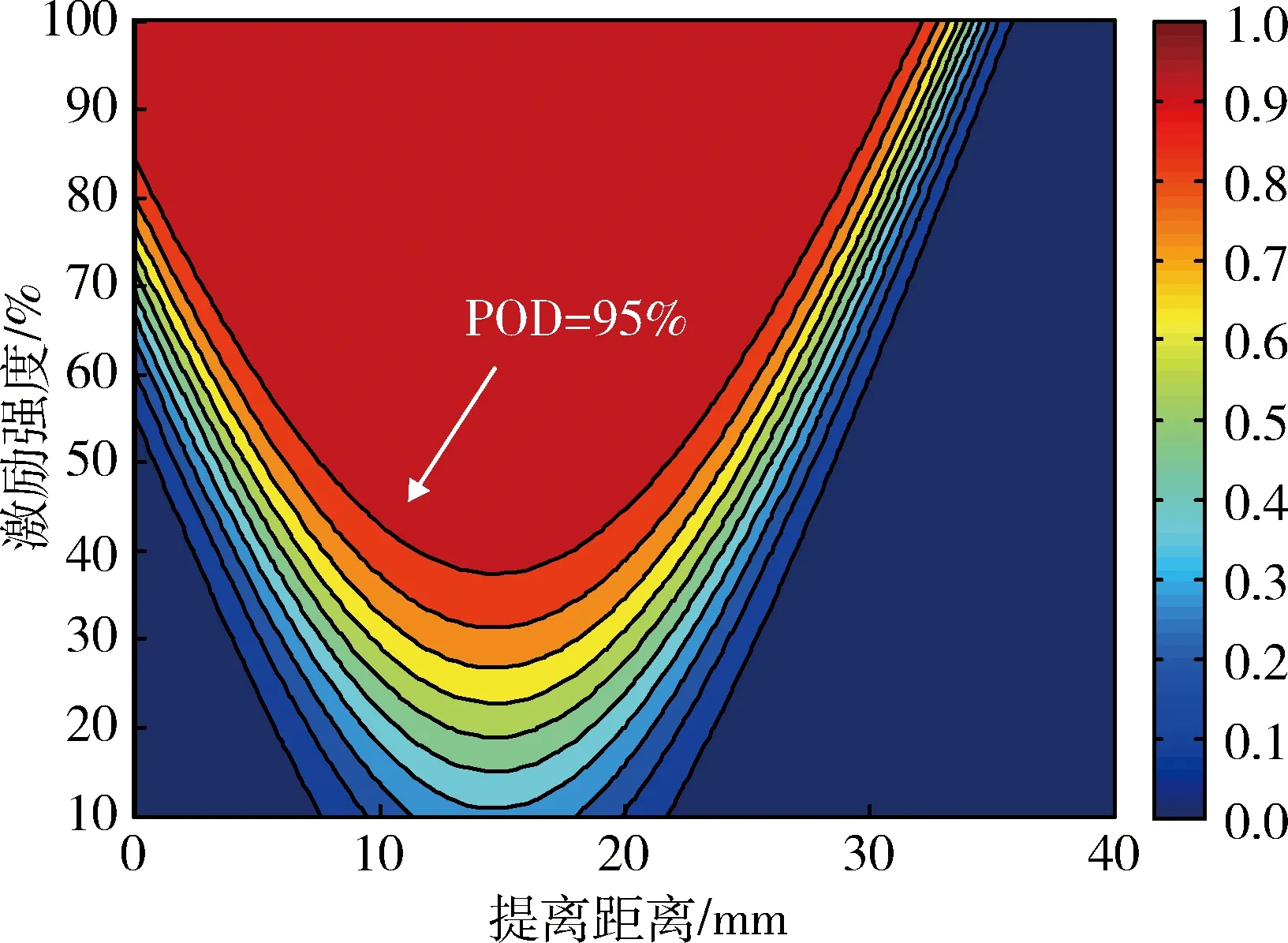
图8 检出概率随检测条件变化的分布云图

4 结论

以热响应信号与检测条件之间的对应关系为切入点，采用控制变量法揭示了提离距离、激励强度和激励时间等检测条件对裂纹区域生热的影响程度和影响方式。根据实验数据对多元非线性回归模型的参数进行拟合并筛选出最优模型，最后得到2种检测条件组合的优化结果。研究成果为涡流脉冲热像技术检测过程中参数的设置提供了依据，但本文只研究了2种检测条件的优化组合，其他参数的检测优化需要进一步探究。

[1] HE Y Z,PAN M C,CHEN D X,et al.Eddy current step heating thermography for quantitatively valuation[J].Applied physics letters,2013,103(19):194101-194105.

[2] BEN W,DARRY P A,PETER C,et al.Eddy current induced thermography-probability of detection study of small fatigue cracks in steel,titanium and nickel-based superalloy[J].NDT & E international,2012,49(4):47-56.

[3] 喻星星.激励参数对铁磁性管结构件脉冲涡流检测的影响及其激励研究[D].南昌：南昌航空大学,2013.

[4] 张超省,宋爱斌,冯辅周,等.超声红外热像检测条件的优化方法研究[J].红外与激光工程,2016,45(2):77-84.

[5] LI J W.Nondestructive test manual[M].Beijing：China Machine Press,2011:22-24.

[6] HOLLAND S H,UHL C,RENSHAW J.Toward a viable strategy for estimating vibrothermographic probability of detection[J].AIP Conf.Proc.,2007,975(1):491-497.

[7] HOLLAND S H,UHL C,ZHONG O Y,et al.Quantifying the vibrothermographic effect[J].NDT & E international,2011,44(8):775-782.

[8] LI M,HOLLAND S H.Quantitative multi-inspection-site comparison of probability of setection for vibrothermography nondestructive evaluation data[J].Journal of nondestructive evaluation,2011,30(3):172-178.

[9] GAO C，MEEKER Q W,MAYTON D.Detecting cracks in aircraft engine fan blades using vibrothermography nondestructive evaluation[J].Reliability engineering and system safety,2014,131(3):229-235.

[10] 冯辅周,张超省,宋爱斌,等.超声红外热像检测中疲劳裂纹的检出概率模型研究[J].红外与激光工程,2016,45(3):50-55.

[11] 何晓群.实用回归分析[M].北京:高等教育出版社,2008:52.

(责任编辑: 尚菲菲)

Optimization Method of Detection Conditions for Metal Fatigue Cracks in Eddy Current Pulsed Thermography

FENG Fu-zhou, XU Chao, MIN Qing-xu, SUN Ji-wei, ZHU Jun-zhen

(Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

In order to explore the influence of different detection conditions on crack heating and its optimal selection, the influence of lift-off distance, incentive strength and time on crack heating is studied by control variable method. Then, based on the effect analysis of those detection conditions on crack hea-ting, a multiple nonlinear regression model is adopted to estimate the Probability Of Detection (POD). of cracks under specific detection conditions, and the optimal selection range of the detection conditions is determined. The optimization method of detection conditions proposed in this paper will provide theoretical direction for detection scheme in Eddy Current Pulsed Thermography (ECPT).

Eddy Current Pulsed Thermography (ECPT); Probability Of Detection (POD); thermal response; fatigue crack

1672-1497(2017)03-0089-05

2017-03-19

军队科研计划项目

冯辅周(1971-)，男，教授，博士。

TG115.28

A

10.3969/j.issn.1672-1497.2017.03.017