基于模糊路面识别的多轮独立电驱动车辆驱动防滑控制
2017-07-05廖自力阳贵兵陈路明
廖自力, 刘 栋, 阳贵兵, 陈路明
(装甲兵工程学院控制工程系, 北京 100072)
基于模糊路面识别的多轮独立电驱动车辆驱动防滑控制
廖自力, 刘 栋, 阳贵兵, 陈路明
(装甲兵工程学院控制工程系, 北京 100072)
为了解决多轮独立电驱动车辆驱动工况下车轮滑转的问题,在整车驱动力分层控制的基础上,提出了一种基于模糊路面识别的模糊滑模控制方法,通过模糊路面识别器实现路面最优滑转率的识别,最后利用ADAMS/View与MATLAB/Simulink进行机电联合仿真。结果表明:该控制方法能够改善车辆驱动防滑效果,验证了其在多轮独立电驱动车辆系统中的有效性。
多轮独立电驱动; 驱动防滑控制; 模糊路面识别; 模糊滑模控制; 系统抖振
稳定性、机动性与灵活性一直是车辆的重要性能指标。与传统机械传动车辆相比,多轮独立电驱动车辆具有全轮独立可控的特性[1]。轮毂电机作为车辆的执行机构,转矩响应快、控制精度高,使整车的机动性和灵活性开发空间增大。但这种分布式驱动形式也对车辆的稳定性控制提出了更高要求,尤其是车辆在越野或低附着路面行驶时,由于各驱动轮附着不均匀,车轮更易发生过度滑转,对整车层面的多电机转矩协调控制产生不利影响。因此,驱动防滑控制(Acceleration Slip Regulation,ASR)作为牵引力控制的核心,其单轮控制效果直接决定了整车的机动性和稳定性。
国内外研究者针对这一问题进行了大量研究工作,将复杂程度不同的控制方法应用到车辆驱动防滑控制中。如:FU等[2]将PID控制方法应用于车辆驱动防滑控制中,控制结构简单,但系统参数固定,对非线性系统控制效果不理想;冯彦彪等[3]采用不依赖于系统模型的模糊控制方法,外界参数变化的干扰对控制效果影响小、鲁棒性强,但模糊控制规则的形成往往依赖于人的经验,控制精度较低;段敏等[4]提出了基于路面识别的自适应模糊PID控制方法,融合了PID控制和模糊控制2种方法的优点,进行了适用于复杂路况条件的车辆防滑控制研究;阳贵兵等[5]采用基于指数趋近率的滑模变结构控制,以车轮角速度和电机转矩为状态变量选取滑模面,结构简单且鲁棒性强,但系统容易产生抖振,影响了控制效果。
滑模变结构控制是一种非线性控制方法,由于滑模面可进行设计且与系统参数及扰动无关,处于滑模运动的系统具有很好的鲁棒性,适用于车辆一类非线性系统。但采用简单滑模变结构控制的缺陷在于系统抖振造成的控制输出高频振动可能对电机造成损害,通过引入模糊控制规则,能够有效减小系统抖振。为此,笔者在整车驱动力分层控制的基础上,以车辆ASR为研究对象,采用基于模糊路面识别[6]的模糊滑模控制方法来实现对车轮的防滑控制。
1 车辆系统建模分析
1.1 车轮动力学分析
为便于建立车辆系统关于车轮滑转率λ的状态空间模型,笔者采用单轮车辆模型,如图1所示。
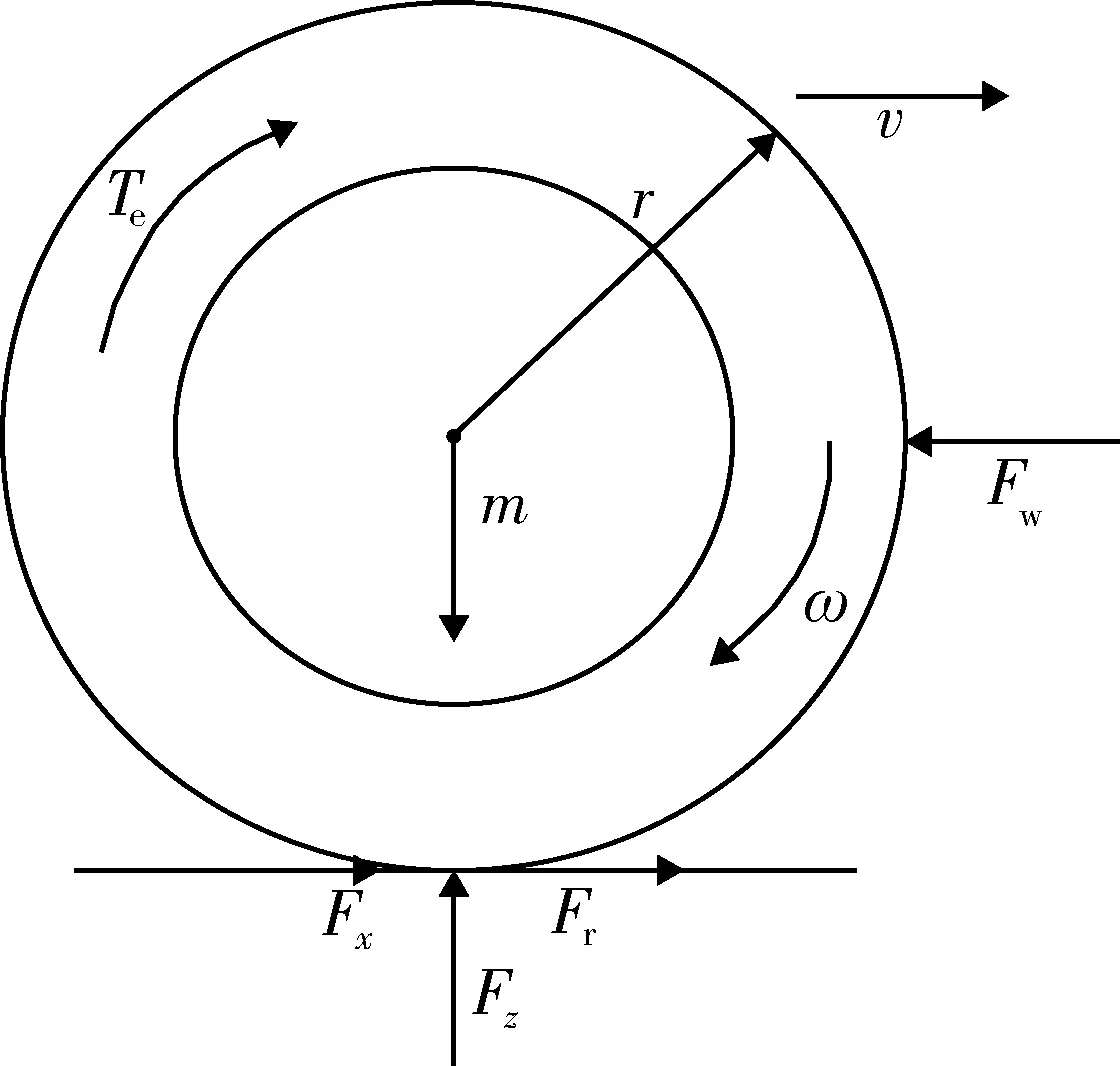
图1 单轮车辆模型
图中:m为整车质量在单轮的分量(按照整车质量的1/8平均分配);v为车辆纵向速度;Fx=μFz,为车轮纵向力,其中μ为路面附着系数,Fz为车轮垂向载荷;Fw=cvv2,为空气阻力,其中cv为空气阻力系数;Fr=cω,为车轮的滚动阻力,其中c为轮胎的滚动阻力系数,ω为车轮角速度;Te为轮毂电机实际输出转矩;r为轮胎有效半径。车辆直线运动方程和车轮滚动方程分别为
(1)
(2)
式中:i为轮毂电机减速器的传动比;J为车轮转动惯量。
1.2 车辆动力学分析
由式(1)可得车轮纵向力Fx,而在车辆的行驶过程中车轮垂向载荷Fz是一个动态变化量。为便于分析,忽略车辆爬坡和越障等影响,只分析车辆在水平路面行驶时的垂向载荷。令q=1,2,分别代表内、外侧车轮,以外侧车轮为例,图2为车辆直驶运动受力分析。图中:M为整车质量;Fd为整车驱动力;Fz_p2为第p(p=1,2,3,4)轴外侧车轮的垂向载荷;ax为车辆纵向加速度;Lp为第p轴车轮到质心的距离;h为车辆质心高度。
各个车轮的垂向载荷Fz_pq为[7]
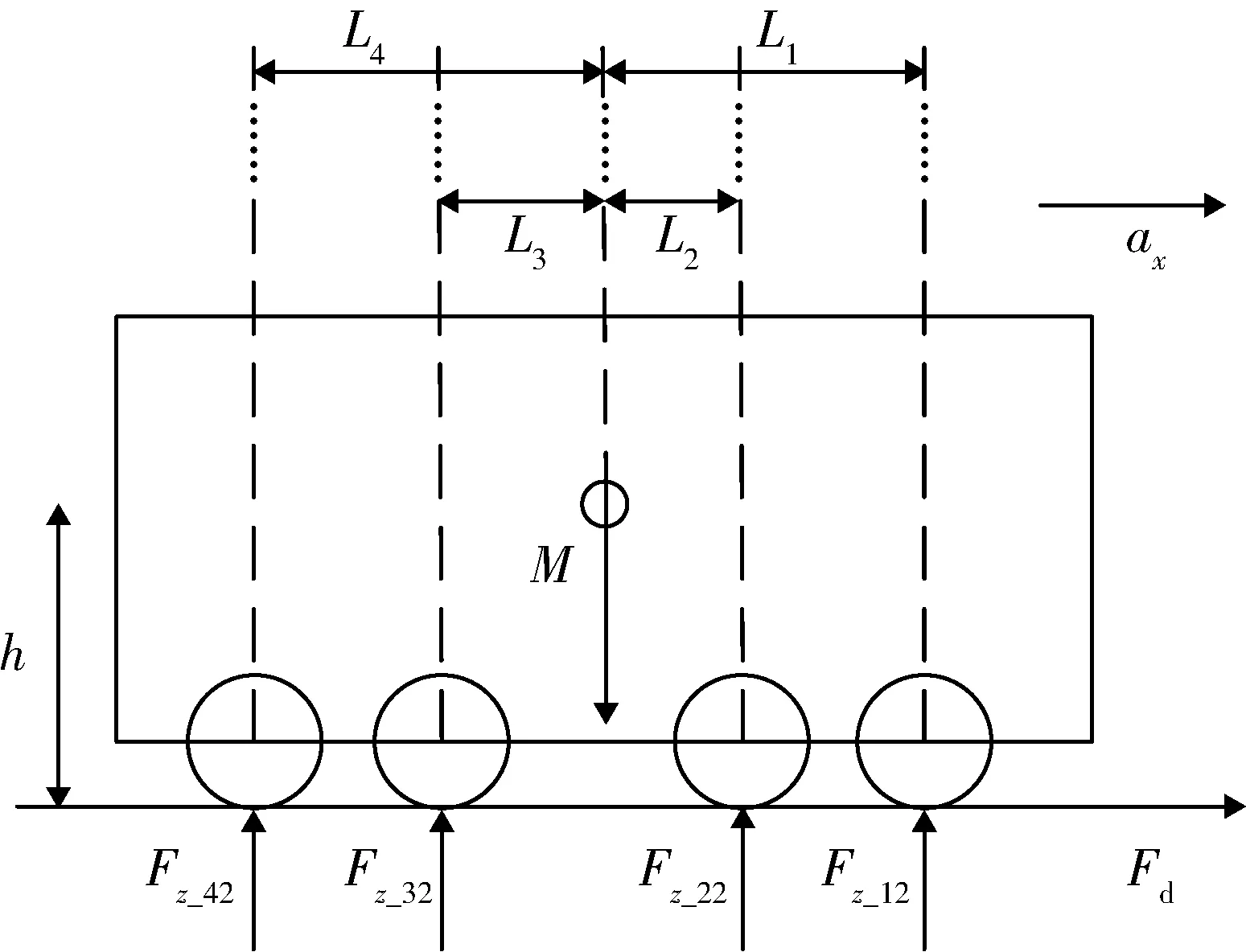
图2 车辆直驶运动受力分析
式中:ay为车辆侧向加速度;B为内外轮距;g为重力加速度;
La=(L1-L2)+(L1+L3)+(L1+L4);
Lb2=(L1-L2)2+(L1+L3)2+(L1+L4)2。
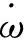
λ=(vω-v)/vω,
(4)
μ=Fx/Fz。
(5)
式中:vω=ωr,为理论车速。令状态变量x1=v,x2=vω,结合式(1)、(2)可得单轮车辆模型状态空间描述为
(6)
(7)
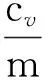
将x1=v,x2=vω代入式(4),并对其两边求导可得
(8)
联立式(6)-(8)可得
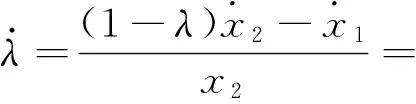
(9)
基于上述动力学分析,单轮车辆模型关于车轮滑转率λ的状态空间表示为
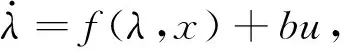
(10)
式中:f(λ,x)={(1-λ)f(x2)-f(x1)+[(1-λ)×c2-c1]μ}/x2;b=c3(1-λ)/x2;u=Te。
由式(10)可知:对该非线性系统进行控制,需要选取合适的控制律,以控制轮毂电机实际输出转矩Te,并使车轮滑转率λ相对于最优滑转率的跟踪误差趋于0。
1.3 驱动电机模型
笔者采用经验方法对驱动电机进行建模,通过对轮毂电机实验数据进行外特性拟合,得到其外特性曲线,如图3[7]所示。
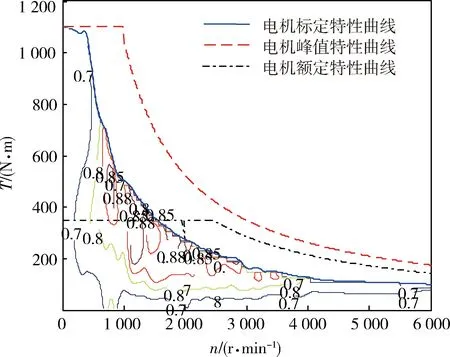
图3 轮毂电机外特性曲线
轮毂电机采用直接转矩控制,则一阶动态系统模型为
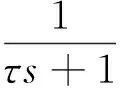
(11)
式中:τ为电机时间常数,用以描述电机响应速度,这里取值为0.005;Tref为电机输出转矩期望值;s为复变量。
根据轮毂电机外特性曲线以及一阶动态系统模型,建立轮毂电机的查表模型,如图4所示。可以看出:轮毂电机作为车辆的执行机构,其输入Tref由防滑控制直接给定,Tref经1个转矩限幅环节和1个惯性环节后输出Te。
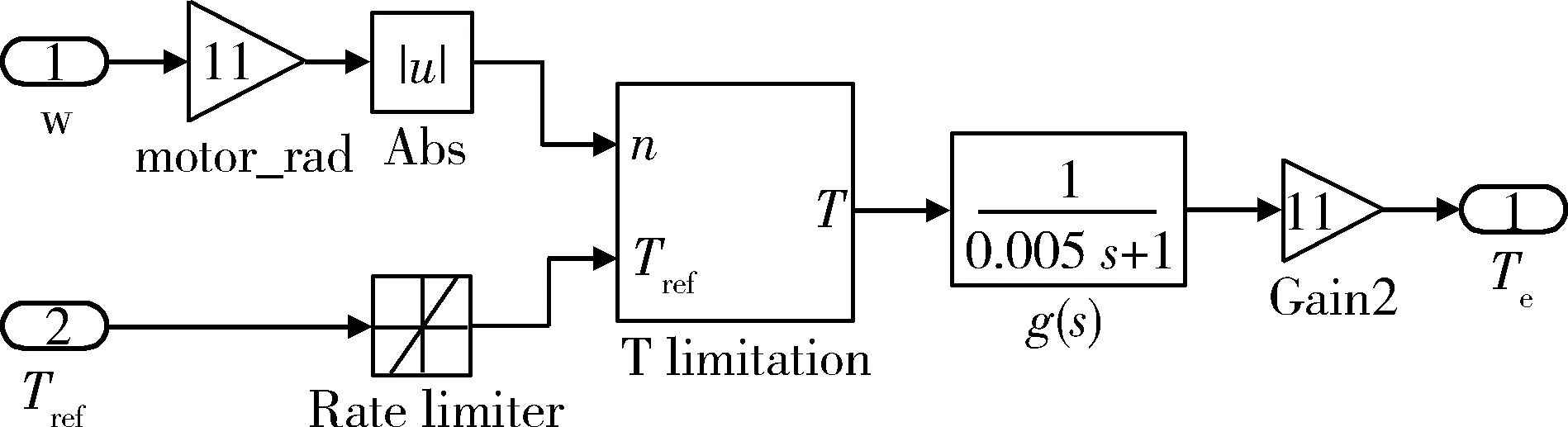
图4 轮毂电机查表模型
2 驱动防滑控制
在整车驱动力控制中,上层控制以驾驶员油门信号为输入计算总转矩需求,根据车辆质心侧偏角和横摆角速度计算横摆力矩,并按照一定的控制策略进行转矩预分配,实现整车纵向驱动力的初步分配控制;下层为防滑控制层,对8个驱动轮分别进行防滑控制,实现对预分配转矩Tref1_j(j=1,2,…,8,代表1-8车轮)的优化。驱动防滑控制系统ASR结构如图5所示,可以看出:ASR主要由模糊路面识别器和模糊滑模控制器2部分构成,以最优滑转率λd和车轮滑转率λ为防滑控制器输入,8个电机的转矩优化值Tref2_j为输出。
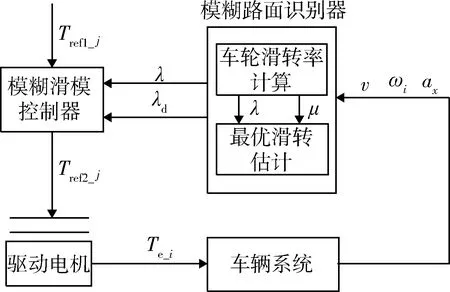
图5 驱动防滑控制系统ASR结构
2.1 模糊路面识别
在实际的工程应用中,由于参数在线辨识困难,不能由公式直接计算出λd,而多轮独立电驱动车辆电机转矩响应快速可测,能够通过传感器获取车辆状态参数。因此,笔者设计了以典型路面μ-λ曲线为基础的模糊路面识别算法。
图6为6种典型路面μ-λ曲线。图7为λ及大、中、小3种滑转率条件下μ的隶属度函数,其中:
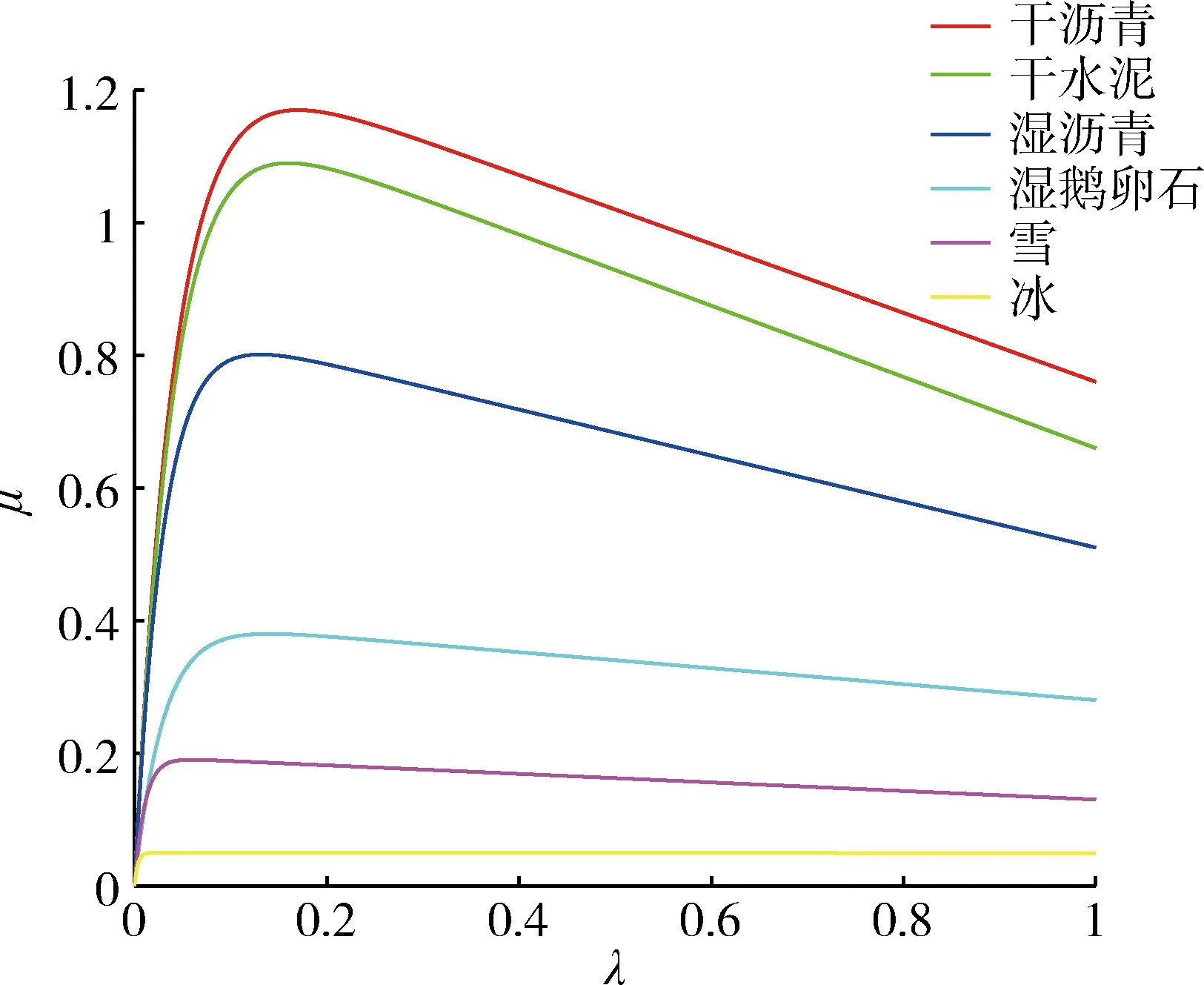
图6 6种典型路面的μ-λ曲线
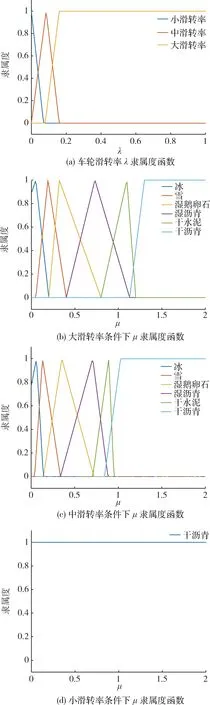
图7 λ及大、中、小3种滑转率条件下μ的隶属度函数
λ的模糊子集为小、中、大滑转率;μ的模糊子集为冰、雪、湿鹅卵石、湿沥青、干水泥和干沥青6种路面。当前路面与6种典型路面的相似程度用xk(k=1,2,…,6,分别代表冰、雪、湿鹅卵石、湿沥青、干水泥和干沥青6种路面)表示,xk的模糊子集为TD、D、GS、S、ES,根据经验分别取值为 0、0.3、0.5、0.8、1。模糊路面识别器的模糊控制规则如表1所示。
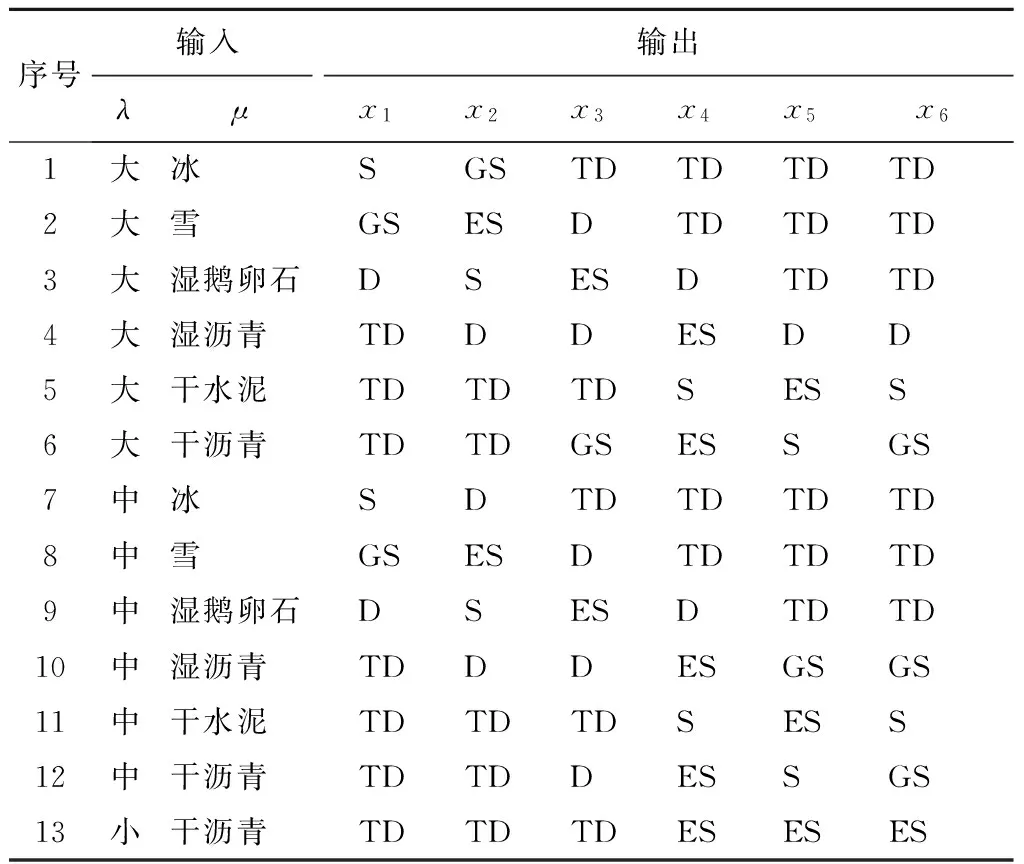
表1 模糊路面识别器的模糊控制规则
以λ、μ作为模糊路面识别器的输入,根据图7确定对应的隶属度函数,完成输入模糊化;以xk为输出,经过输入模糊化、模糊控制规则设计和模糊逻辑推理后,采用加权平均法求解模糊化,得到当前路面最优滑转率λd和最大附着系数μmax分别为
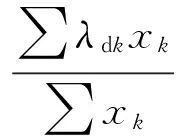
(12)
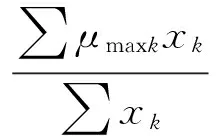
(13)
式中:λdk为典型路面的最优滑转率;μmaxk为典型路面的最大附着系数。
2.2 防滑控制器设计
2.2.1 模糊滑模控制结构
等效滑模控制的控制律通常由等效控制ueq和切换控制us组成,即u=ueq+us。其中:等效控制保证系统状态处于滑模面上,而切换控制则迫使系统状态在滑模面上滑动[8],保证了滑模控制的鲁棒性,但同时也造成了系统抖振。
利用模糊控制规则对切换控制项进行模糊化处理,使其在干扰较大时增大、在干扰较小时减小,从而减小抖振。引入模糊系数α,其模糊滑模控制结构如图8所示。
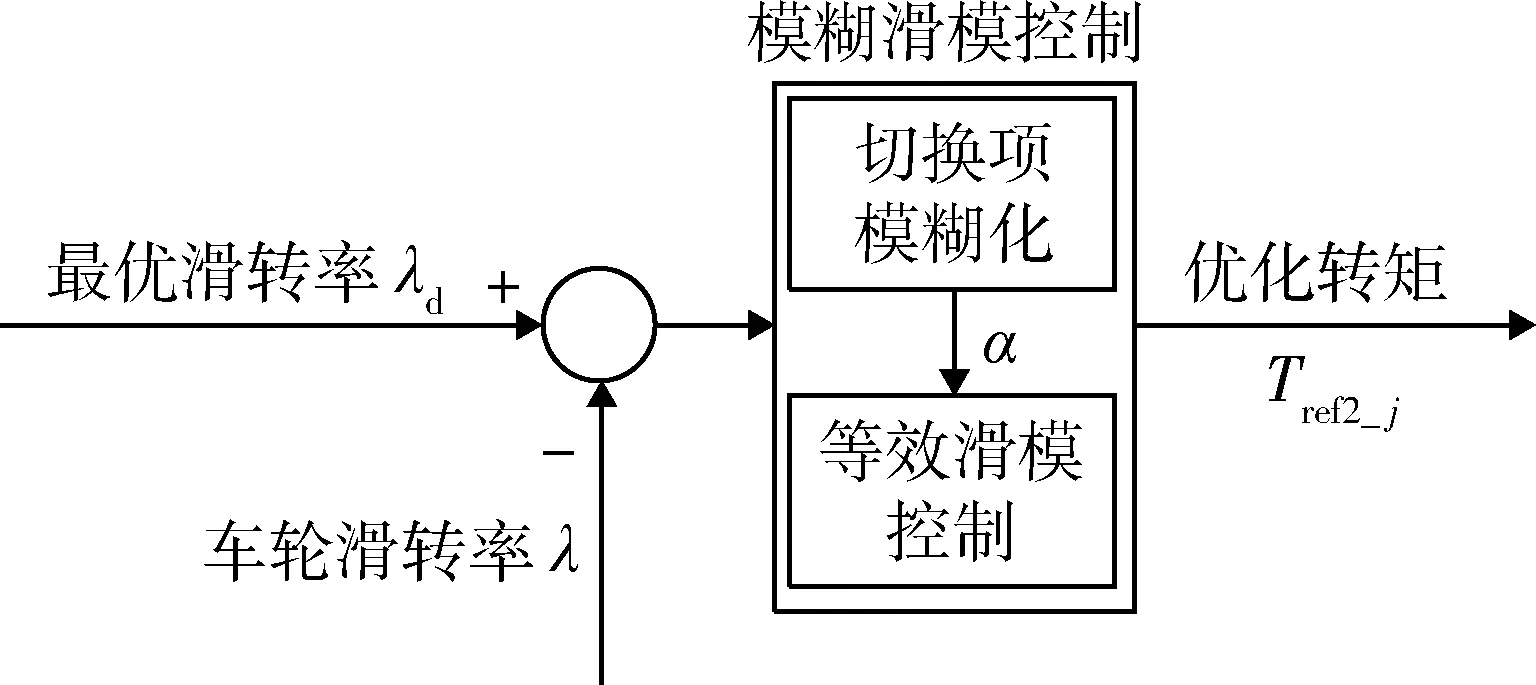
图8 模糊滑模控制结构
2.2.2 模糊滑模控制律设计
设计滑模函数为
S=λd-λ,
(14)
(15)
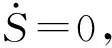
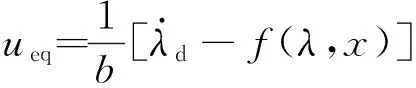
(16)
设计系统的切换控制us为
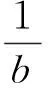
(17)
等效滑模控制律u为
(18)
取李雅普诺夫函数为
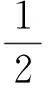
(19)
要求系统稳定,取β>0。
建立模糊系统,其输入为滑模函数S,输出为切换控制的模糊系数α[9],输入/输出隶属度函数如图9所示,模糊规则如下:
其中:模糊子集Z、P、N分别表示“零”“正”“负”。当系统无干扰时,取α=0,此时控制律只由等效控制项构成;当系统干扰较大时,取α>0,此时控制律由等效控制和切换控制构成。
综上所述,模糊滑模控制律为
u=ueq+α·us。
(20)
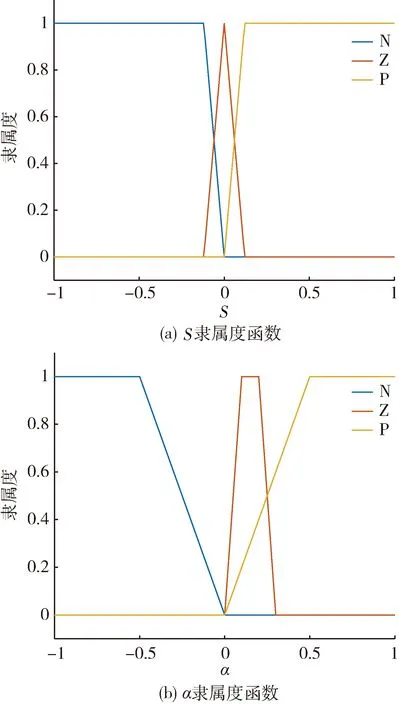
图9 模糊系统输入/输出隶属度函数
3 联合仿真分析
根据防滑控制系统结构及模糊滑模控制方法设计特点,在MATLAB/Simulink中建立防滑控制系统仿真模型[10],如图10所示。利用ADAMS/View建立车辆动力学模型,包括车身、悬架、转向系统、轮胎及路面模型。其中:轮胎模型采用UA轮胎模型,仿真路面在ADAMS/Car中通过Road Builder根据仿真环境设定要求进行三维建模,可以设置不同的路面条件。
机电联合仿真主要分析和验证车辆在单一附着路面和变附着路面条件下直线行驶时模糊滑模控制器的防滑控制效果,联合仿真模型如图11所示。由于仅考虑车辆直线行驶工况,因此不需计算横摆力矩。车辆总驱动力矩需求Td为
(21)
式中:η为驾驶员通过加速踏板输入的油门信号,取值为[0,1];Tmax(nj)为当前转速下第j个电机能够输出的最大扭矩,通过车辆系统反馈的ω值折算得到。仿真时,通过给定η值来确定预分配转矩Tref1_j。
3.1 单一附着路面仿真
设置路面附着系数μ=0.2,油门信号η=0.5,以左侧车轮为分析对象。图12为有、无防滑控制时车速和轮速曲线,其中ω1、ω3、ω5、ω7分别为4个车轮转速,可以看出:无防滑控制时,4个车轮发生滑转;施加防滑控制后,车轮滑转现象得到明显改善。图13为第1轴车轮滑转率曲线,可以看出:车辆运行2 s后,车轮滑转率基本稳定在最优滑转率0.12附近。图14为轮毂电机输出转矩曲线,其中Te_1、Te_3、Te_5、Te_7分别为4个轮毂电机输出转矩,可以看出:通过防滑控制调节,电机输出转矩值始终小于驾驶员给定,且保持良好的电机外特性;当施加防滑控制后,最高车速从约10 m/s提高至约15 m/s,说明车辆动力性能得到了提高。

图10 防滑控制系统仿真模型
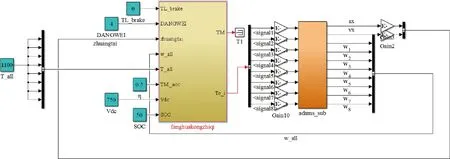
图11 联合仿真模型
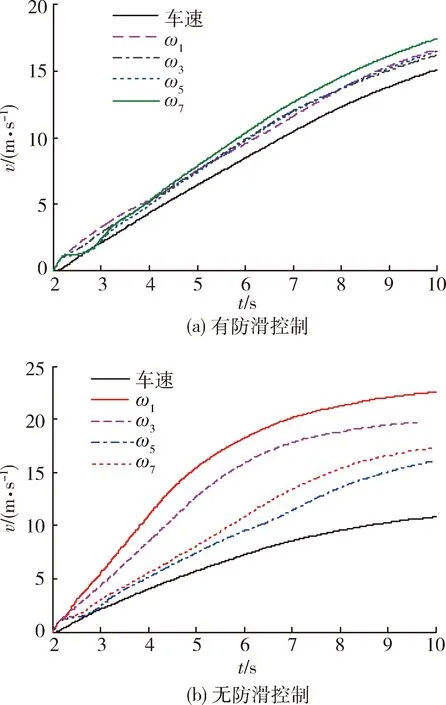
图12 有、无防滑控制时车速和轮速曲线
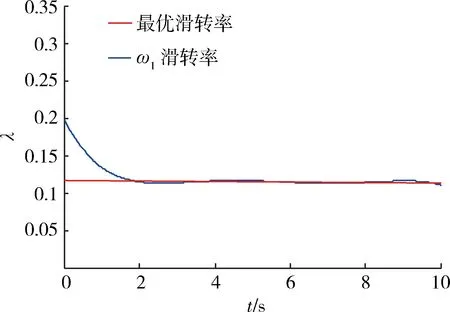
图13 第1轴车轮滑转率曲线
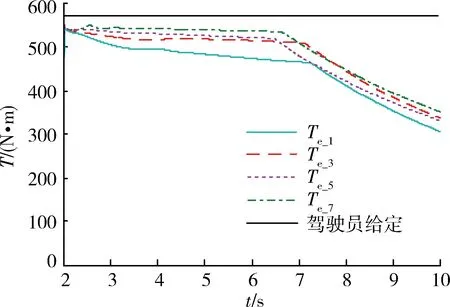
图14 左侧轮毂电机输出转矩曲线
3.2 变附着路面仿真
设置路面为低附着与高附着对接路面,其路面附着系数分别为 0.2、0.85,驾驶员通过加速踏板输入油门信号η=0.5,车辆在2 s时进入高附着路面。图15为第1轴左侧车轮滑转率曲线和轮毂电机输
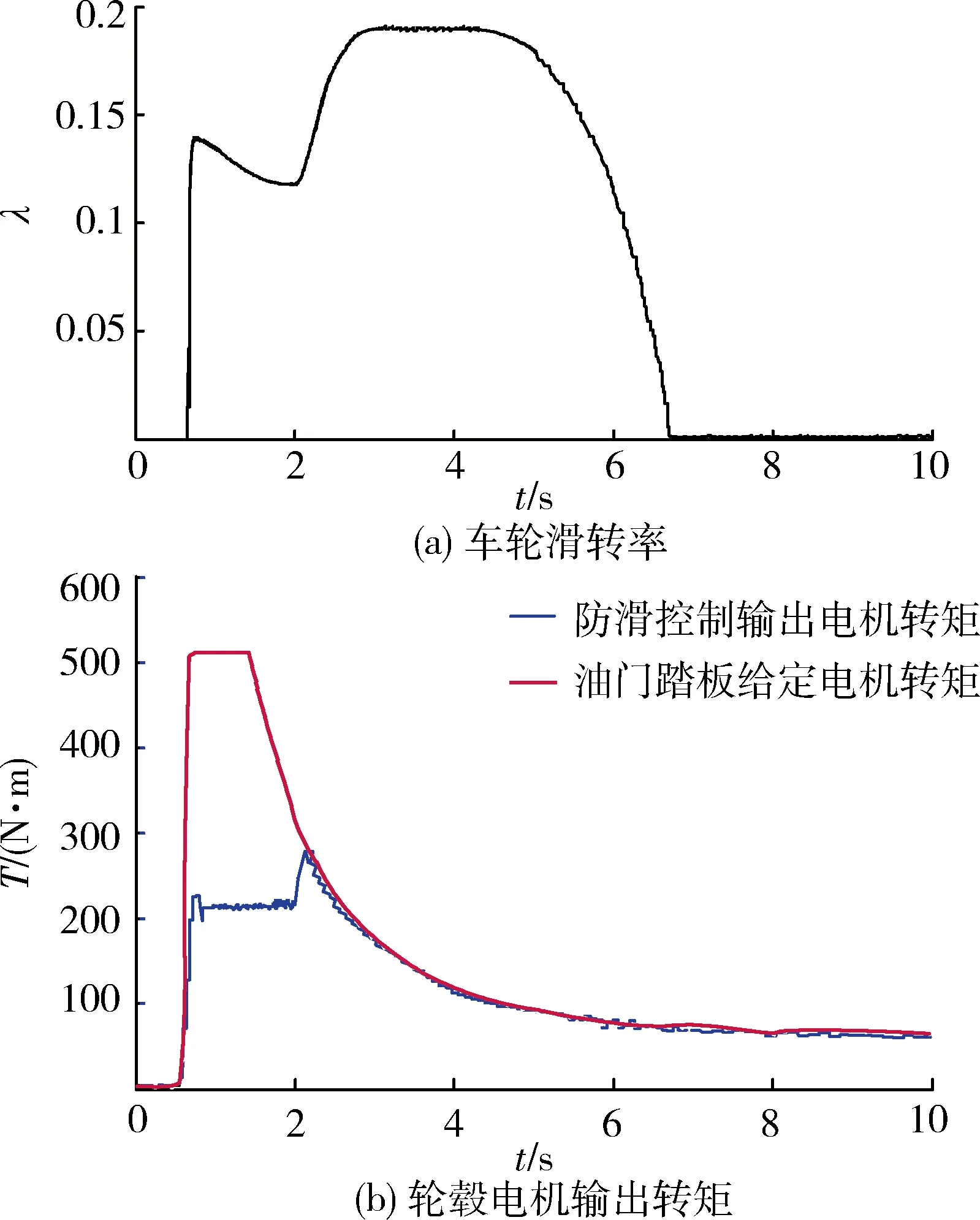
图15 第1轴左侧车轮滑转率曲线和轮毂电机输出转矩曲线
出转矩曲线。可以看出:车辆在低附着路面行驶时,第1轴左侧车轮滑转率基本保持在0.12左右,防滑控制使电机输出转矩得到调节;进入高附着路面后,路面附着系数增大,车轮滑转率保持在0.18左右,基本不发生滑转,防滑控制输出转矩与油门踏板给定转矩基本一致。
4 结论
针对多轮独立电驱动车辆系统,建立了基于MATLAB/Simulink的车辆驱动防滑控制系统仿真模型和基于ADAMS/View的车辆动力学模型,设计了基于模糊路面识别的模糊滑模控制器,通过联合仿真实验分析了车辆有、无防滑控制情况下车速、轮速、车轮滑转率及电机输出转矩等参数的变化情况,验证了控制方法的有效性。
然而,本研究只针对车辆直线行驶工况,而在实际行驶过程中,车辆转向时车轮发生滑转的情况更为严重。下一步,将针对转向时的防滑控制进行控制策略的优化改进,并对驱动、制动2种工况下防滑控制的一体化集成进行研究。
[1] 邱斌斌.多轮独立电驱动车辆驱动力分层控制策略[D].杭州:浙江大学,2015.
[2] FU Q,ZHAO L J,SUN X L,et al.Study on anti-slip regulation of quarter automobile based on PID control[C]∥Proceedings of the 2nd International Conference on Consumer Electronics,Communications and Networks.Yichang,China:IEEE,2012:2111-2114.
[3] 冯彦彪,杨珏,季智燚,等.基于最优滑转率的电动车辆驱动防滑控制策略[J].农业工程学报,2015,31(8):119-125.
[4] 段敏,郭文涛,李刚,等.基于路面识别的电动汽车驱动防滑控制策略研究[J].机电工程,2015,32(9):1257-1262.
[5] 阳贵兵,廖自力,马晓军,等.多轮独立电驱动车辆驱动力优化控制研究[J].兵工学报,2016,37(1):23-30.
[6] 蒋振江,陈旭,李大伟.基于路面识别的四轮驱动电动汽车驱动防滑控制[J].重庆理工大学学报(自然科学版),2012,26(7):17-22.
[7] 阳贵兵.8×8轮毂电机驱动装甲车辆行驶驱动与稳定性控制研究[D].北京:装甲兵工程学院,2016.
[8] 刘金琨.滑模变结构控制MATLAB仿真:基本理论与设计方法[M].3版.北京:清华大学出版社,2015:69-74.
[9] 戴彦.汽车ABS滑移率的模糊滑模控制研究[J].机械设计与制造,2015(6):80-82.
[10] 王正林,王胜开,陈国顺,等.MATLAB/Simulink与控制系统仿真[M].北京:电子工业出版社,2012:44-64.
(责任编辑: 尚菲菲)
Acceleration Slip Regulation of Multi-wheel Independent Electric Drive Vehicle Based on Fuzzy Road Surface Identification
LIAO Zi-li, LIU Dong, YANG Gui-bing, CHEN Lu-ming
(Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China)
To solve the slip problem of multi-wheel independent electric drive vehicle during driving off, based on a hierarchical control structure applied to the whole vehicle, a fuzzy sliding mode control method based on fuzzy road surface identification is proposed, which obtains the optimal slip ratio of the road surface through the fuzzy road surface identification device. The results of mechanical-electrical co-simulation using ADAMS/View and MATLAB/Simulink show that the anti-slip control method can improve the anti-slip effect during vehicle driving off, and verify the effectiveness of the method in multi-wheel independent drive electric vehicle system.
multi-wheel independent electric drive; acceleration slip regulation; fuzzy road surface identification; fuzzy sliding mode control; system chattering
IfSis N thenαis P;
IfSis Z thenαis Z;
IfSis P thenαis P。
1672-1497(2017)03-0046-07
2017-01-03
军队科研计划项目
廖自力(1974-),男,副教授,博士。
TJ81+0.34
A
10.3969/j.issn.1672-1497.2017.03.009
