考虑履带环的履带车辆振动响应分析

乔新勇， 段 誉， 芮 强， 王红岩

(装甲兵工程学院机械工程系， 北京 100072)



考虑履带环的履带车辆振动响应分析

乔新勇， 段 誉， 芮 强， 王红岩

(装甲兵工程学院机械工程系， 北京 100072)

为了准确描述履带车辆的振动特性，通过对履带车辆行动系统拓扑结构的分析，建立了柔性履带模型和刚性履带模型，采用特征值方法计算了履带环的固有振动特性，并利用功率谱方法对仿真结果进行了对比，分析了履带对车辆振动特性的影响，最后通过实车试验对所建模型的准确性进行了验证。结果表明：履带对车辆振动的影响主要包括履带环的低阶固有振动和与履带板节距相关的高频振动；2类模型的计算误差在2%～27%之间，说明履带对车辆系统振动的影响范围较大，根据不同工况可选择合适的模型进行计算。

履带； 振动响应； 动力学仿真； 履带板节距； 功率谱密度； 特征值分析

由于履带对车辆振动的影响，使得履带车辆在越野路面上行驶时的振动响应与轮式车辆有很大区别，因此建立准确的履带车辆动力学模型是研究车辆振动响应的重要手段。考虑到履带对车辆振动特性影响的复杂性，如何在履带车辆动力学模型中对其进行准确的描述是确保模型计算精度的关键。尽管文献[1-3]作者分别建立了不同的履带车辆数学模型，但均未全面考虑履带特别是履带环的影响。SCHLOAR等[4]提出了基于连续弹性体履带的履带车辆系统模型，为分析履带的振动特性提供了参考。文献[5-6]作者基于DADS软件分别建立了采用刚性履带和未采用刚性履带的履带车辆模型，对比分析了履带车辆振动响应的差异。尽管研究人员采用多种方法建立了考虑履带影响的履带车辆模型，提高了模型的计算精度，但并未对履带自身的振动特性以及履带如何影响车辆的振动进行深入研究。

鉴于此，笔者基于多体动力学原理建立分别包含柔性履带和刚性履带的履带车辆行动系统模型，采用特征值分析法和功率谱分析法研究履带环的固有振动特性，对比分析2类模型的振动响应结果。研究结果对定量描述履带对车辆振动特性的影响，并进而改善履带车辆的振动特性具有重要意义。

1 履带车辆行动系统动力学建模

为了开展履带对车辆振动响应特性的对比研究，笔者通过分析履带车辆行动系统的拓扑结构和动力学方程，分别建立了简化履带的柔性履带行动系统模型和考虑履带板之间复杂约束关系的刚性履带行动系统模型。

1.1 拓扑结构分析

以某型高速履带车辆为例，基于多体动力学原理建立车辆行动系统模型，为方便计算，进行如下简化：1)假设所有部件均为刚体，其中上装、动力传动系统与车体合并为单个质量块；2)悬挂装置由平衡肘与车体间的弹簧阻尼力矩代替；3)张紧机构中曲臂通过转动副连接诱导轮和车体，其传动装置简化为通过平动副和弹簧阻尼力约束的滑柱和套筒，二者通过转动副分别与车体、曲臂相约束[7-8]。

在柔性履带模型中，为了简化履带部分的建模，假设柔性履带是由不可伸长的带子环绕各轮而成，与各个车轮间为轴平行约束，与硬路面通过接触力约束。即忽略履带板之间的相互作用关系，认为柔性履带与各车轮之间只有运动学约束关系，因而该模型无法反映履带的复杂振动特性。

在刚性履带模型中，根据履带板的几何尺寸构建单块履带板的几何实体模型。其中：履带板与主动轮、负重轮、诱导轮及托带轮之间的相互作用关系按接触力处理；履带板之间由被橡胶轴套包裹的履带销连接，相邻履带板与履带销的作用力简化为履带销处的轴套力和摩擦力矩，在忽略摩擦力矩的情况下，履带板间的接触力为产生平动和转动效应的力和力矩[9]。

根据上述简化，结合履带车辆各部件间的连接关系，得到的柔性履带和刚性履带的履带车辆行动系统拓扑结构如图1所示，其模型部件和约束详情见表1、2。其中：柔性履带和刚性履带的履带车辆行动系统模型的自由度数目分别为122和1 182个。

1.2 行动系统动力学方程

采用笛卡尔坐标系下的第一类拉格朗日方程建立高速履带车辆行动系统动力学方程。刚体的质心笛卡尔坐标和反映刚体方位的欧拉角组成其广义坐标，即qi=(x,y,z,ψ,θ,φ)T。履带车辆模型广义坐标矩阵为

表1 履带车辆行动系统模型部件

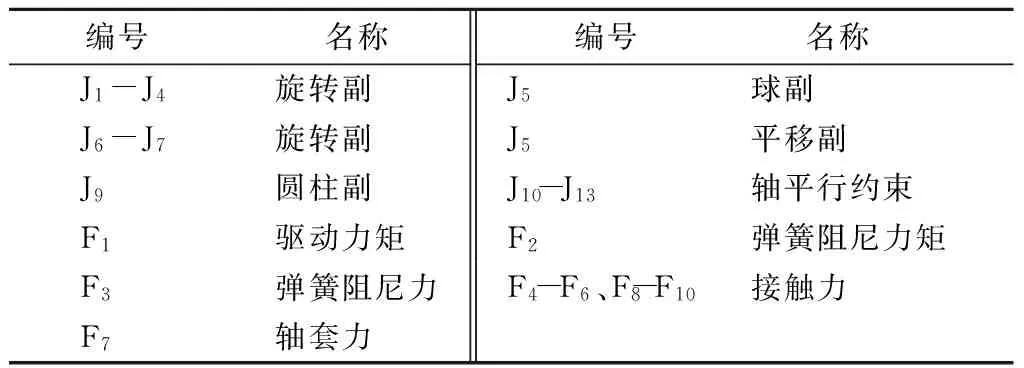
表2 履带车辆行动系统模型约束

q=(q1,q2,…,qn)T，

(1)

履带车辆模型中刚体的约束方程为

φ(q,t)=0，

(2)

式(2)对时间求导，得到速度约束方程为

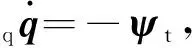
(3)

式(3)对时间求导，得到加速度约束方程为

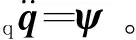
(4)

履带车辆模型中，刚体的动力学方程为

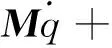
(5)

式中：M为履带车辆模型的广义质量矩阵；λ为拉格朗日乘子；Fe为广义外力矩阵；Fv为惯性力矩阵。

联合式(4)、(5)，得到动力学模型的欧拉-拉格朗日方程组为

(6)

根据上述理论分析，并结合实际的车辆设计参数，构建履带车辆行动系统动力学模型，用于后续的仿真计算。

2 履带振动特性分析

履带车辆行驶过程中，履带对车辆振动的影响主要有2方面：1)履带环的约束作用和履带环固有振动的影响；2)履带板与地面之间的相互作用以及履带与主动轮啮合过程中产生的多边形效应。两者分别影响履带车辆的低频振动和高频振动。

2.1 履带环固有振动特性分析

为了研究履带环的固有振动特性，将履带车辆模型中的履带环作为连续弹性体进行分析，非接地段履带环模型由第1负重轮、第6负重轮、诱导轮、主动轮和托带轮之间的6段履带组成，如图2所示。图中：Uj、Vj分别为第j段履带的纵向振动位移和垂向振动位移，其中j=1,2,…,6；θ1，θ2…，θ5为分别主动轮、3个托带轮、诱导轮的角位移。

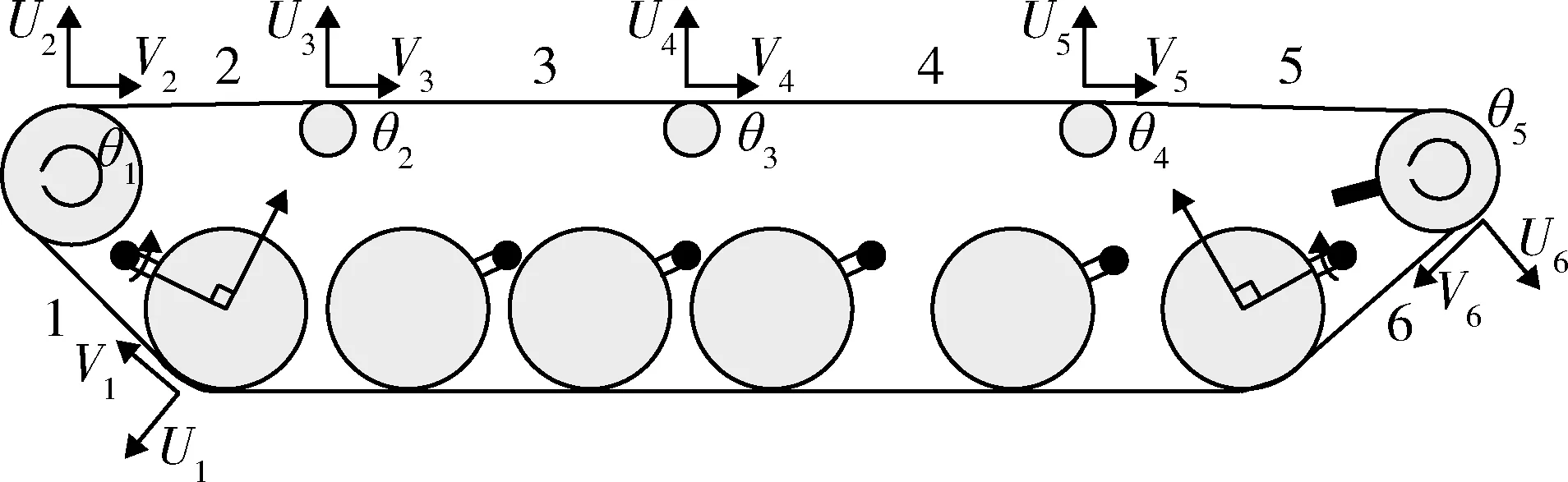
图2 非接地段履带环模型

2.1.1 连续弹性体履带的振动分析

用连续弹性体模型来描述履带在平面内的振动状态，如图3所示。可以看出：附着于两轮间的履带在自身重力作用下产生下垂，达到静平衡位置时近似为抛物线，其曲率为K。令函数V(x,t)、U(x,t)分别表示履带纵向振动位移和垂向振动位移，其中：x∈(0,L)，为履带微元的位置坐标，L为该段履带的长度；t为时间变量。

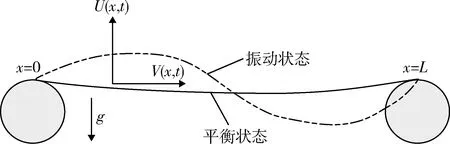
图3 履带平面内振动状态

由牛顿定律得到履带模型自由振动的运动微分方程为

(7)

(8)

式中：

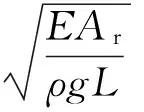
(9)

为纵向波的传播速度，其中ρ为履带的密度，g为重力加速度，E为履带的轴向系数，Ar为履带的纵剖面面积；

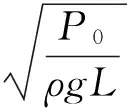
(10)

为垂向波的传播速度，其中P0为履带的预紧张力。

将振动波的传播速度离散为垂向传播速度和纵向传播速度，其后者远大于前者，则可认为履带的拉伸是准静态的。因此，式(7)中描述履带的纵向运动可近似为静态，即

(11)

将式(11)对x进行2次积分，得

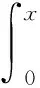
(12)

式中：F(t)、G(t)均为关于t的积分项。

采用分离变量法，设上述函数的通解为

(13)

式中：ω为固有频率。将式(13)代入式(7)、(8)中，可得到纵向振动位移和垂向振动位移分别为

(14)

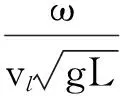
2.1.2 履带环模型特征值计算

为简化计算，对履带环模型作出如下假设：1)车辆运动时履带不会从各轮上滑脱；2)履带环各处线密度和轴向刚度均相同；3)不考虑履带接地段的振动。通过履带的纵向振动、垂向振动和各轮转动3种运动形式，分析履带自由振动的边界条件。

1)在主动轮、托带轮、诱导轮处，由履带位移的连续性可得前后两段履带的纵向位移相同，第1、6负重轮处的纵向位移为0，即纵向振动的边界条件为

(15)

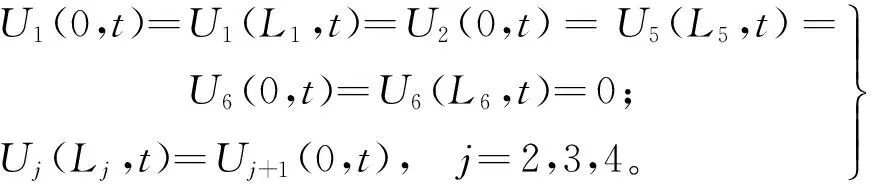
(16)

3)各段履带的动应变一致，相邻段履带的动应变差值导致了其附着的各轮的转动，其转动角度与履带振动的纵向位移相关，则有如下关系:

(17)

式中：I1，I2，…，I5，r1，r2,…，r5和ε1，ε2,…，ε5分别为主动轮、3个托带轮和诱导轮的转动惯量、半径和动应变。

将通解式(14)代入边界条件(15)-(17)中，得到特征值方程为

R(ω)·H=0，

(18)

式中：R(ω)为关于特征值函数的24×24矩阵；H为包含24个常数项的特征向量，即

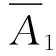
(19)

求解得到履带环的固有振动频率f，其前5阶的固有振动频率及其振型如图4所示。可以看出：履带环的固有振动频率在3～10 Hz的频带范围内，属于低频振动。分析其原因为：当车辆在典型起伏路面行驶时，地面的起伏波动容易引起履带环的低频垂向振动，造成上支履带环的上下波动，严重时上支履带板可能会撞击车体两侧的翼子板，对车辆造成一定的损伤；此外，履带环对行动部分有几何约束和力学约束作用，前者反映在履带环周长固定，后者体现为履带的张紧力，主要影响车辆的低频振动[10]。

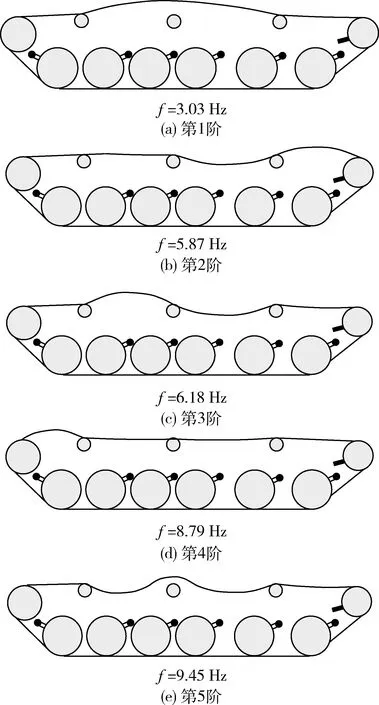
图4 履带环前5阶固有振动频率及其振型

2.2 履带板节距引起的振动响应分析

路面激励通过履带传递时，由于刚性履带板与地面近似为部分点接触，相当于将路面离散成以履带板节距为间隔的路面，滤掉了路面激励中波长大于履带板节距的成分，使这一空间频率成为路面激励的空间频率上限；另外，履带板与主动轮啮合时的多边形效应，使主动轮齿与履带销产生周期性碰撞。这两部分的周期性激励均由履带板节距l引起，激振频率同时与车速u相关，则有

f′=u/(3.6l)。

(20)

对于选定车型，履带板节距l=0.153m。当车辆以高于1挡的速度(10km/h左右)行驶时，履带板节距引起的激振频率范围在18Hz以上，与履带环的固有振动频率相比，属于高频振动。

3 履带车辆系统振动响应分析

为研究履带对车辆振动的作用规律，进行上述2种模型在多种典型工况下的动力学仿真，输出给定激励下驾驶员座椅处的垂向振动响应信号。其中：车速取20、30 km/h，路面等级为D、E、F级，采样频率为200 Hz，采样时间为10 s(不包括落车以及车身恢复平稳时间)。

采用Welch算法计算得到的不同工况下加速度功率谱密度如图5所示，可以看出：加速度信号的频率成分主要分为15 Hz以内的低频段和30 Hz以上的高频段，其中只有刚性履带会激发高频成分。具体分析如下：

1)1.0～2.0 Hz的低频带范围内主要反映的是车体整体的俯仰振动固有频率和垂直振动固有频率。在不同工况下，2类模型计算得到的俯仰振动固有频率和垂向振动固有频率分别在0～0.8Hz和1.3～2.0 Hz的频率范围内变化，这是因为在模型简化过程中，2类模型的系统属性存在一定差异，其中刚性履带模型还受到履带环的几何约束影响。

2)4.0～10 Hz的较低频带范围内主要包含负重轮轴距引起的轴距效应以及履带环的整体振动效应。2类模型在此频带范围内的峰值频率不同、振幅峰值差异不大，这是因为柔性履带模型和刚性履带模型均存在轴距效应，但履带环的约束导致后者受到抑制，同时刚性履带模型中履带环的固有振动效应比较显著。

3)30～60 Hz的高频成分为与刚性履带板节距相关的周期性激励。在刚性履带模型中，当车辆分别以20、30 km/h时速度行驶时，D、E、F级路面下在计算得到的相应峰值频率分别为35.16、36.91、35.55 Hz和54.32、54.35、54.14 Hz，与履带板激振频率理论推算值36.33、54.64 Hz具有很好的一致性。而在柔性履带模型中，由于不考虑履带的作用，因此无法反映履带对高频振动的影响。

表3为2种模型中驾驶员座椅处垂向振动加速度功率谱密度均方根值的对比结果。可以看出：随着路面不平度等级的降低和车速的减小，履带对车辆振动的影响均有所减小，即在车辆行驶过程中，履带部分的振动响应与路面恶劣程度和车速均呈负相关；另外，在不同的工况下，2类模型的均方根值误差在2%～27%，说明履带对车辆振动的影响随工况变化的范围较大。

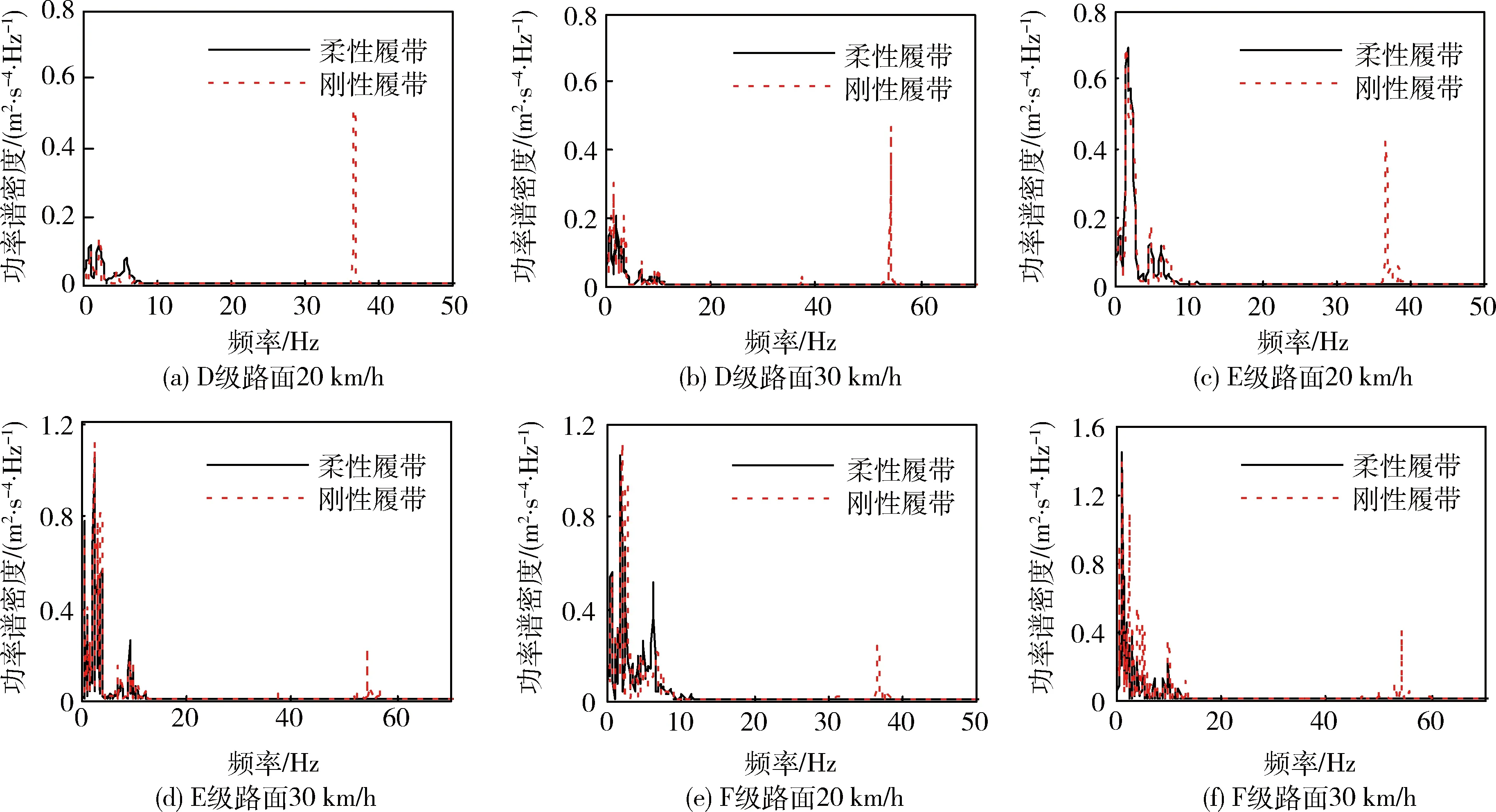
图5 不同工况下加速度功率谱密度

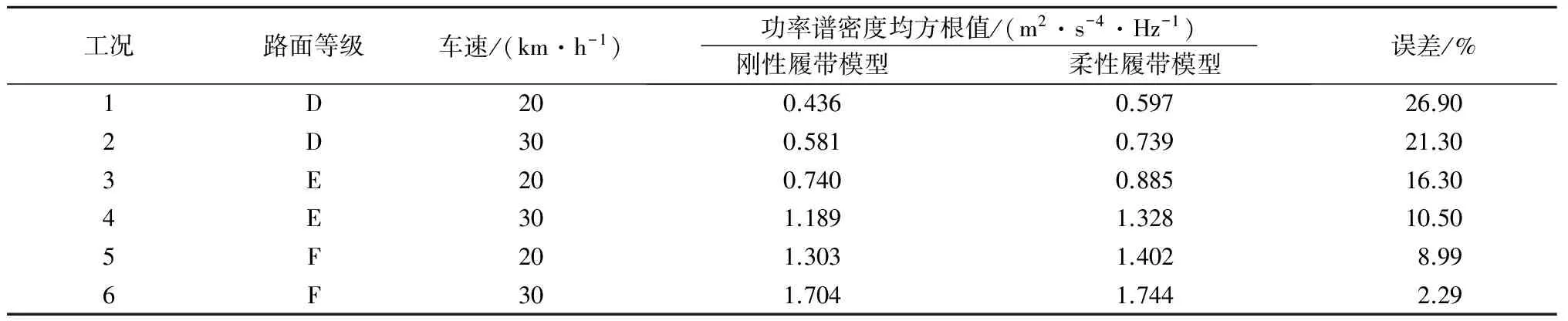
表3 2种模型中驾驶员座椅处垂向振动加速度功率谱密度均方根值对比

柔性履带模型的自由度数目约为刚性履带模型的1/10，解算速度相对更快，计算效率更高。而柔性履带模型和刚性履带模型的低频振动响应较为接近，计算结果的差异主要与高频振动响应幅值的大小有关，受路面等级和车速的影响较大。因此，可根据实际需求具体分析不同工况，选择更为合适的模型。如：在不平度等级接近甚至超过F级的路面上行驶时，可使用不考虑履带影响的模型，在提高计算效率的同时保证一定的可靠性。

4 实车试验验证

在某试验场进行高速履带车辆振动试验，测试装置及试验道路如图6所示，通过NI数据采集系统采集车辆行驶过程中炮长座椅处垂向加速度信号。

选取车速为20、30 km/h时炮长座椅处的垂向加速度测试信号进行频谱分析，得到的功率谱密度曲线如图7所示。可以看出：实车振动的高频成分频带范围较宽，这是由于实车试验中速度呈现较大的扰动性，使得由履带板节距引起的激振频率不断变化；2类模型的仿真结果与实车试验结果的低频振动响应一致，刚性履带模型的高频振动峰值频率与实车试验结果相近，同时其主峰值频率的幅值高于试验结果，说明刚性履带模型由于车速稳定，其高频振动响应较为集中，而柔性履带模型没有高频响应。

因此，刚性履带模型要比柔性履带模型更能真实地反映实车的振动响应特性。但在路况极恶劣的情况下，2种模型相差较小，此时采用柔性履带模型可提高计算效率，具有一定的参考价值。

5 结论

针对如何描述履带对履带车辆振动特性影响的问题，笔者建立了简化履带的柔性履带行动系统模型和考虑履带板之间复杂约束关系的刚性履带行动系统模型，分析了履带环的振动响应特性，并进行了仿真计算和实车试验验证，得出结论如下：

1)履带环的固有振动频率在3～10 Hz的较低频带范围，而履带与地面之间的相互作用以及履带板与主动轮啮合时引起的高频振动与履带板节距和车速相关；

2)相比柔性履带模型，刚性履带模型的仿真结果与实车试验结果更加接近，但路况恶劣时两者相差很小，此时采用柔性履带模型可提高计算效率；

3)驾驶员座椅处垂向振动加速度功率谱密度均方根值误差在2%～27%，说明履带对车辆振动的影响与工况相关，随着路面不平度等级的降低或者车速的减小，履带对车辆振动的影响逐渐变小。

研究结果更详细地描述了履带对车辆振动的影响，定量分析的结果表明建立的2类模型分别适用于不同的工况，为研究如何提高履带车辆的平顺性提供了依据。

[1] 丁法乾.履带式装甲车辆悬挂系统动力学[M].北京：国防工业出版社，2004:67-77.

[2] MARCELLO C.Computational methods for the dynamics and stress analysis of multibody track chains[D].Chicago:University of Illinois at Chicago,1998.

[3] 史力晨，王良曦,张兵志.装甲车辆平顺性仿真及试验验证[J].车辆动力与技术,2004(1):43-47．

[4] SCHOLAR C,NOEL P.Efficient vibration modeling of elastic vehicle track systems[J].Journal of sound and vibration,1999,228(5):1057-1078.

[5] HAN B K,LI X L,WANG C T.Track model and analysis of high-speed tracked vehicles[J].Journal of system simulation,2003(15):1774-1777.

[6] 孟磊,李晓雷,邱实，等.履带对履带车辆车体振动影响的分析[J].车辆与动力技术,2015(4):1-5.

[7] 王钦龙，王红岩，芮强.基于多目标遗传算法的高速履带车辆动力学模型参数修正研究[J].兵工学报,2016,37(6):969-978.

[8] 马伟标，王红岩，芮强.基于广义简约梯度算法的履带车辆模型参数修正[J].系统仿真学报,2012,24(4):774-779.

[9] 王钦龙.高速履带车辆多体动力学建模及试验场道路试验方法研究[D].北京：装甲兵工程学院,2016.

[10] 芮振伟.履带链环约束作用分析[J].兵工学报,1995(1)：9-17.

(责任编辑: 尚菲菲)

Vibration Response Analysis of Tracked Vehicle Considering Track Circuit

QIAO Xin-yong, DUAN Yu, RUI Qiang, WANG Hong-yan

(Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

In order to accurately describe the vibration of tracked vehicle, the flexible track model and the rigid track model are built up through the analysis of the topological structure of operation system of tracked vehicle. The inherent vibration performance is calculated by eigenvalue analysis. Power spectrum method is used to compare the simulation result and analyze the effect of track on the vibration of vehicle. In the end, real vehicle test is used to verify the accuracy of the model. The results show that the effect of track on the vibration of vehicle mainly include the inherent vibration of track circuit and the high frequency vibration related to track pitch; the error between two models is 2%-27%, which shows that the track affects the vibration response of vehicle in great scope, and different models can be chosen according to different working conditions.

track; vibration response; dynamic simulation; track pitch; power spectral density; eigenva-lue analysis

1672-1497(2017)03-0039-07

2017-03-30

乔新勇(1970-)，男，副教授，博士。

TJ81+0.33; TP391.9

A

10.3969/j.issn.1672-1497.2017.03.009